Физика свистков

Свисток — это устройство, которое издает звук за счет воздуха, выдуваемого с одного конца и проходящего через небольшое отверстие на противоположном конце. Их форма позволяет воздуху нестабильно колебаться внутри камеры. Физическая теория процесса звукоиздания является примером применения гидродинамики или гидродинамики и аэродинамики . Принципы, относящиеся к работе свистка, также находят применение в других областях, таких как измерение расхода жидкости.

Типы

Уилсон и др. в своем исследовании человеческого свиста. ^[1] (см. ниже), указал на важность включения симметрии или асимметрии неустойчивого течения в дополнение к перечисленным ниже классам обратной связи. Из-за тесной связи симметрии потока с генерируемым звуковым полем их концепция была включена сюда как часть описания источника звука (монопольный – симметричный и диполь – асимметричный).

Монополь

Свистки, которые генерируют звук за счет колебаний массового потока через границу, называются монополеподобными источниками. Рисунок справа представляет собой пример небольшой сферы, объем которой колеблется. Для этого типа источника звук излучается радиально, поэтому звуковое поле одинаково во всех направлениях и затухает обратно пропорционально квадрату расстояния. Звуковую мощность можно выразить как:

W_{\text{m}}={\frac {\pi \rho _{0}}{c_{0}}}{\widehat {Q}}^{2}{\text{St}}^{2}U^{4}L^{2}

Переменные U и L считаются характерными для источника, и важен их правильный выбор.

Диполь

Свистки, которые генерируют звук за счет колебаний импульса или напряжения и деформации силы, действующей на окружающую среду, называются дипольными источниками. Рисунок справа представляет собой пример небольшой твердой сферы, которая движется вперед и назад в заданном направлении. Это приводит к неоднородному звуковому полю. Звуковую мощность можно выразить как:

W_{\text{d}}={\frac {3\pi \rho _{0}}{c_{0}^{3}}}{\hat {F}}^{2}{\text{St}}^{2}U^{6}L^{2}

Категории отзывов

Аэродинамические свистки основаны на нестабильности потоков и обратной связи, усиливающей нестабильность. Существует несколько способов возникновения обратной связи. ^[2]

Категория I

Звук свистка этой категории в первую очередь является побочным продуктом движения источника. Обратная реакция недостаточна для строгого контроля движения источника, поэтому свистки не относятся к этой категории.

Категория II

Обратная реакция среды является определяющим фактором движения источника. Нестабильное движение жидкости или генерируемый ею звук могут иметь обратную связь с источником и управлять им. Что требуется:

источник стабильной мощности;
механизм усиления, который может преобразовывать постоянную мощность в изменяющуюся во времени мощность;
возмущение, вызывающее усиливаемые колебания;
средство генерации звука или другого колебательного броуновского движения жидкости;
средство обратной связи об этом колебательном движении как помехе на входе усилителя.

Свистки относятся к этой категории. Есть несколько способов описать процесс обратной связи.

Класс I

Обратная связь по существу несжимаема; скорость звука хотя и конечна, но достаточно велика, чтобы ее можно было считать бесконечной. Это действие можно назвать гидродинамической обратной связью. Существует ряд устройств класса I.

Класс II

Обратная связь сжимаемая и не зависит от скорости звука. Это действие можно назвать квазисжимаемой обратной связью.

Класс III

Обратная связь сжимаемая и зависит от скорости звука. Это можно назвать акустической обратной связью.

На рисунке справа показана блок-схема этих механизмов обратной связи. Все аэродинамические свистки относятся к одному из классов.

Этапы

Обратная связь в свистках – это нелинейная механика или хаос. Из-за нелинейности можно иметь более одной частоты при заданном расходе. Разница зависит от того, достигается ли скорость потока за счет увеличения потока или за счет уменьшения потока. Возможность множественных состояний называется стадией и схематически показана на рисунке справа. По мере увеличения скорости потока ( число Рейнольдса , Re) частота медленно возрастает (почти постоянное число Струхаля , St), но затем частота резко возрастает до более высокого уровня. По мере последующего уменьшения скорости потока частота медленно снижается, но затем резко снижается до более низкой ступени. Эта закономерность называется гистерезиса петлей .

Более высокие стадии связаны с большим количеством вихрей на этом расстоянии, что указывает на то, что это расстояние может быть важным характерным измерением. В нескольких свистках были выделены три стадии. Чрезмерное звучание некоторых музыкальных духовых инструментов приводит к переходу стадии I на ступень II.

Нестабильность потока

Нестабильность потока является двигателем свиста. Он преобразует постоянную энергию в энергию, зависящую от времени.

Пример показан на рисунке справа со струей воды. ^[3] Ламинарная двумерная струя усиливает небольшие возмущения в отверстии, создавая вихревую дорожку . В этом случае скорость потока, выраженная в числе Рейнольдса, была построена в зависимости от частоты возмущений, выраженной в числе Струхаля, для различных амплитуд возмущений, чтобы выявить область нестабильности, как показано на рисунке слева. Значение D на рисунке представляет собой отношение смещения бокового возмущения к ширине сопла; беспорядки были минутными.

Одним из важных источников нестабильности жидкости является наличие градиента скорости или слоя сдвига с точкой перегиба. При свисте нестабильность начинается в какой-то точке трехмерной области, а затем движется по некоторому пути в этой области по мере изменения локальных переменных. Это очень затрудняет всестороннее понимание механизмов нестабильности свистков.

Масштабирование

Свистки бывают разных форм и размеров, но их работу можно унифицировать с помощью концепций динамического и геометрического подобия с помощью анализа размерностей . Природа ничего не знает о конкретных системах измерения, которые мы используем; его волнуют только соотношения между различными силами, временными масштабами и несколькими измерениями. Для их сравнения необходимо учитывать установленные соотношения, имеющие отношение к работе свистка.

Сходство лучше всего выявляется путем определения скорости U , то есть характерной для динамики, и размерности L , то есть характерной для геометрии. Если эти значения использовать в безразмерных числах, таких как перечисленные ниже, можно достичь большего понимания этого явления.

Он натер число

{\text{St}}={\frac {fL_{1}}{U}},\quad {\text{St}}_{a}={\frac {fL_{2}}{c_{0}}}

Первое число представляет собой отношение нестационарных сил инерции к постоянным силам инерции. Число было названо в честь Винсенка Струхаля , который первым вывел зависимость между частотой образования вихрей вокруг цилиндра и скоростью потока. Характеристическими переменными были диаметр цилиндра L ₁ и скорость U обтекания его.

Это число позволяет установить взаимосвязь между различными размерами и скоростями. Это уравнение можно назвать жидкостно-механическим числом Струхаля по сравнению со второй версией, которую можно назвать акустическим числом Струхаля. Первый вариант используется для динамического подобия движения жидкости в свистах, а второй вариант — для динамического подобия акустического движения в свистах. Многие свистки требуют использования обоих номеров.

число Маха

M={\frac {U}{c_{0}}}

Это отношение постоянной скорости к скорости звука . Число было названо в честь Эрнста Маха , который впервые изучил (помимо прочего) сверхзвуковые течения и ударные волны. Это число описывает диапазон между потоками, которые можно считать сжимаемыми, и потоками, которые сжимаются.

число Рейнольдса

{\text{Re}}={\frac {UL}{\upsilon }}

Это отношение постоянных сил инерции к постоянным силам вязкости . Число было названо в честь Осборна Рейнольдса , инженера, проведшего новаторские исследования перехода ламинарного течения в турбулентное в трубах.

Число Россби

{\text{Ro}}={\frac {U}{f_{0}L}}

Это отношение линейной скорости к тангенциальной скорости для закрученных потоков. Частота характеризует скорость вращения потока. Число было названо в честь Карла-Густава Россби , метеоролога, который первым описал крупномасштабные движения атмосферы с точки зрения механики жидкости.

Безразмерная сила

{\hat {F}}={\frac {F}{\rho _{0}U^{2}L^{2}}}

Отношение фактической динамической силы к установившемуся импульсу и постоянной плотности тока.

Безразмерный объемный расход

{\hat {Q}}={\frac {Q}{UL^{2}}}

Отношение динамического объемного расхода к установившемуся объемному расходу.

Монопольные свистки

В этих свистках неустойчивость потока симметрична, что часто приводит к периодическим кольцевым вихрям , а генерация звука связана с колебаниями объемного/массового расхода.

Дырочный тон (свисток чайника, крик птицы)

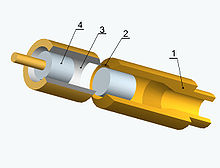
Стационарный поток из круглого отверстия можно преобразовать в колебательный поток, добавив выходную пластину с круглым отверстием, совмещенным с отверстием. Небольшие возмущения потока в обратной связи отверстия с отверстием вызывают переменный объемный расход через выходное отверстие из-за симметрии обратной связи. Возмущение в струе представляет собой симметричное вихревое кольцо , которое движется с некоторой скоростью медленнее, чем средняя скорость струи, пока не встретит отверстие, и некоторое количество жидкости проталкивается через него, что приводит к возникновению монопольноподобного звукового поля в полупространстве снаружи. На рисунке справа показана схематическая геометрия.

Чтобы вызвать динамическое сходство, ^[4] характерная скорость в исследовании была выбрана как средняя скорость U струи на отверстии, а характерная длина была выбрана как диаметр отверстия δ . Испытания проводились на пяти расстояниях h / δ от отверстия. Были использованы два закона масштабирования: число Струхаля было построено в виде графика как функция числа Рейнольдса. Результаты показаны на рисунке справа.

Частота тона определяется тем, как часто вихрь встречался с отверстием, двигаясь с некоторой скоростью u, меньшей начальной скорости струи. Поскольку струя замедлялась по мере продвижения к дыре, скорость вихря вместе с ней замедлялась, поэтому частота и число Струхаля были больше на меньшем расстоянии. Данные по числу Струхаля ясно показали почти линейную зависимость между частотой и начальной скоростью струи. На четырех из протестированных дистанций были прыжки между I и II этапами. Петли гистерезиса являются четким указанием на сложную природу структуры усиления неустойчивости струи.

Однородность измеренного звукового поля для этого свистка подтвердила его монопольную природу. Измерения зависимости уровня звука от скорости показали, что он очень близок к U ⁴, что еще раз подтверждает монопольную природу источника. При таких скоростях и расстояниях обратная связь обычно относилась к классу II, но отражение поверхностей на расстоянии до 3 метров и при правильной фазировке контролировало тон, переводя обратную связь в класс III.

Дырочный тон также известен как свисток чайника. ^[5] Они обнаружили, что выше числа Рейнольдса 2000 работа дырочного тона происходит с симметричной эволюцией вихря и постоянным числом Струхаля с числом Рейнольдса. На более низких скоростях цилиндрический объем реагировал как резонатор Гельмгольца . Барон Рэлей ^[6] знал об этом свисте; тогда это называлось птичьим криком . В Австралии есть лисий свисток Тентерфилд. ^[7] и традиционный лисий свисток , который, кажется, действует как дырочные звуки.

Свисток из гофрированной трубы

Этот свисток имеет десятки народных названий. Гофрированные трубы или трубы часто используются в различных целях, поскольку их легче сгибать, чем традиционные трубы. Устойчивый поток через гофрированную трубу при низких числах Рейнольдса приводит к колебаниям объемного расхода, что создает монопольно-подобное звуковое поле на выходе из трубы. Примеры таких труб показаны на рисунке справа.

Желтая пластиковая трубка, показанная на изображении, представляет собой игрушку, которая свистит, когда трубку вращают. Показанная металлическая труба использовалась в кабине Конкорда для подачи охлаждающего воздуха пилотам, но ее удалили из-за ее громкого звука. Этот свисток во многом схож с дырочным тоном, в частности свистком чайника. Он подвержен скачкам частоты и петлям гистерезиса. Об этом свистке есть множество статей в Интернете, он изучен в научной литературе. ^[8]^[9]^[10]

Характеристическая скорость — это средний поток U через трубу, а характеристическая длина должна быть кратна расстоянию L между гофрами, nL , где n — целое число. На низких скоростях нестабильному внутреннему потоку необходимо пройти несколько гофров, чтобы установить контур обратной связи. По мере увеличения скорости петлю можно создать с меньшим количеством гофров. Простые тесты были проведены с желтой пластиковой трубкой.

Число Струхаля

{\text{St}}={\frac {f_{n}nL}{U}}

использовался в качестве масштабного коэффициента. Самая высокая частота (7554 Гц) была обнаружена в «раздутом» состоянии, а n предполагалось как одно гофро. При наименьшей скорости потока частота 2452 Гц выгодно отличалась от n = 3. При промежуточных скоростях потока одновременно возникало несколько негармонически связанных частот, что позволяет предположить, что в генерации звука участвуют несколько гофров. В меньшей металлической трубке преобладающий тон появился на частоте 6174 Гц и соответствовал n = 2. Уникальность этого свистка состоит в том, что внутренний поток несет как нестабильный вихрь вниз по течению, так и возвращающийся сигнал обратной связи вверх по течению.

Трубочный тон (Пфайфентон)

Уникальная особенность этого свистка в том, что звук звучит только при прохождении через отверстие снаружи; это акустический диод. Известно, что цилиндрическая полость с небольшим круглым отверстием с квадратными краями на одном конце и полностью открытым на другом производит звук, когда через нее проходит воздух. Он подвержен скачкам частоты и петлям гистерезиса, подобным дырочному тону. Судя по всему, существует две ступени, и обратная связь, вероятно, относится к классу II, если трубка короткая. Основной тон возникает вблизи λ = 4 L , поэтому один характерный размер — это L , длина трубки. Характеристическая скорость U — это скорость потока через отверстие.

Звуковое поле, подобное монополю, создается колебаниями объемного расхода. Картик ^[11] и Андерсон ^[12]^[13]^[14] изучили это явление и пришли к выводу, что движущей силой является симметричное образование вихрей со стороны полости.

Пример этого устройства показан на рисунке справа; у него было отверстие диаметром 0,125 дюйма (3,2 мм), длина 1,9 дюйма (48 мм) и диаметр 0,8 дюйма (20 мм). Расчетная частота четвертьволнового резонанса составила 1780 Гц, а измеренная основная частота составила 1625 Гц с обнаруживаемыми второй и третьей гармониками. Конечные поправки на излучение отверстий необходимы для согласования двух частот. торцевых поправок необходимы два дополнительных размера: диаметр d1 _{отверстия} и диаметр d2 _{Для определения} трубки.

Хартманн, свистки Гальтона (форштевень)

Если предыдущие свисты возникали при низких скоростях потока, то этот свист возникает при очень высоких скоростях. Когда дозвуковая струя сталкивается с полостью, нестабильность струи становится частью петли обратной связи, как и в случае с тоном отверстия. Когда сверхзвуковая струя сталкивается с полостью, неустойчивость акустической ударной волны становится частью контура обратной связи. Рисунок справа — один из примеров этого свистка. Цилиндрическая полость с одним открытым концом, обращенным к сверхзвуковой круглой струе, создает чрезвычайно интенсивный звук. Фигуры на рисунке представляют ячейки ударной волны/расширения внутри струи. Соответствующая конфигурация, называемая жиклером штока , имеет центральный стержень в жиклере, который выдвигается для поддержки и выравнивания полости. Существует несколько других геометрических вариаций, все из которых действуют схожим образом, например, паровой свисток .

Эти устройства были изучены, ^[15] и рассмотрен Раманом. ^[16] Здесь мы смотрим прежде всего на свисток Хартмана. Ударные ячейки струи взаимодействуют с скачком скачка перед каверной (течение в каверне дозвуковое). Небольшие симметричные возмущения в струйном потоке усиливаются по мере продвижения к полости (в некоторых отношениях аналогично звуку отверстия), вызывая колебания ударной волны перед полостью. Ударный фронт действует во многом как поршневой источник высокой энергии, в результате чего создается звуковое поле, подобное монополю. Опять же, объемный поток направлен, в отличие от теоретического монополя.

Звуковое поле может быть похоже на создаваемое колебательным потоком из трубы, за исключением наличия структуры сверхзвуковой струи, которая может сильно изменять направленность. Исходное уравнение Хартмана показано ниже:

{\begin{aligned}{\frac {\lambda }{d}}&=5.8+2.5\left({\frac {h}{d}}-\left(1+0.0041(P-0.9)^{2}\right)\right)\\{\text{St}}&={\frac {fd}{c_{0}}}\approx 0.17\approx {\frac {fh}{U}}\end{aligned}}

Диаметр отверстия и полости - d , расстояние между отверстием и полостью - h , а давление в отверстии P задавалось в килограммах силы на квадратный метр (1 кгс/м). ² ≈ 9,8 Па). На нижнем пределе h второе слагаемое исчезает. В этом случае уравнение можно было бы переформатировать в терминах акустического числа Струхаля, как показано во втором уравнении выше. Характеристической скоростью U в сопле является скорость звука c ₀ . Интересно, что это число очень близко к найденному Струхалем для обтекания цилиндра. Есть два характерных масштаба длины. Диаметр сопла d характеризует мощность звука, а расстояние h характеризует частоту.

Комплексные исследования этого явления ^[17]^[18] показали, что положение полости имеет решающее значение для создания звука. Процесс имеет петли гистерезиса, а частоты связаны с кратными четвертьволновому резонансу резонатора. После переформатирования формулы Хартмана и использования новой формулировки, приведенной выше, уравнение звуковой мощности можно записать как

{\begin{aligned}W_{h}&={\frac {\rho }{2}}{\frac {\pi d^{2}}{4}}(2\pi fa)^{2}c_{0}\\&=A\rho f^{2}d^{2}h^{2}c_{0}\\&=A{\frac {\rho }{c_{0}}}\left({\frac {fd}{c_{0}}}\right)^{2}c_{0}^{4}a^{2}\\&=A{\frac {\rho _{0}}{c_{0}}}{\text{St}}^{2}U^{4}L^{2}\end{aligned}}

Поскольку характеристическая скорость U и скорость звука по существу одинаковы, ее можно переписать в виде второго уравнения. Это уравнение имеет ту же структуру, что и уравнение для точечного монополя, показанное выше. Хотя амплитудный коэффициент A заменяет безразмерный объемный расход в этих уравнениях, зависимость от скорости убедительно подтверждает монопольные характеристики свистка Хартмана. На рисунке справа показан двоюродный брат свистка Хартмана — свисток Гальтона . Здесь полость возбуждается кольцевой струей , которая симметрично колеблется вокруг острых краев полости. Похоже, что это круговая версия краевого тона (обсуждается ниже), в которой симметрия дипольного источника краевого тона преобразуется в монопольный источник.

Поскольку весьма вероятно, что колебания когерентны по периферии, должна быть колеблющаяся объемная скорость потока из полости с лишь небольшой чистой боковой силой. Таким образом, источником является еще одна версия монопольноподобной геометрии; объемный расход представляет собой цилиндрическую область между струей и полостью.

Богатая трубка

Есть несколько свистовых явлений, в которых тепло играет роль. Температура звуковой волны варьируется, но поскольку это изменение настолько мало, обычно его влиянием пренебрегают. Однако, когда может произойти усиление, небольшое изменение может вырасти и оказать важное влияние на создаваемое звуковое поле. Самый известный тепловой свисток — трубка Рийке , вертикальная трубка с помещенным внутри нагретым марлевым материалом.

Первоначально марлю нагревали с помощью горелки Бунзена; позже проволочную сетку стали нагревать электрически. Тепло, передаваемое воздуху в трубке, приводит к почти полуволновому резонансу, если сетка расположена ниже средней точки трубки, как показано на рисунке справа. Теоретически оптимального положения не существует, так как скорость волны вверх равна c ₀ + u , скорость конвекции, а скорость волны вниз равна c ₀ − u . Без конвекционного потока лучшими местами для теплопередачи являются середина и нижний конец трубы. При конвекции обычно выбирается компромиссное положение на полпути между двумя точками, которое зависит от количества добавленного тепла. Одной характеристической длиной, связанной с частотой, является длина L. трубки

Другой характерной длиной, связанной с мощностью звука, является αL , положение сетки. Характеристическая скорость должна быть скоростью конвекции u у источника тепла. Подробное изучение свистка см. Матвеев. ^[19] Поскольку резонанс первой моды составляет около полуволны, звуковое поле, излучаемое трубкой, исходит от двух синфазных источников, похожих на монополи, по одному на каждом конце. Газовое пламя внутри трубки может вызвать резонанс; его называли поющим пламенем . Имеется обратная трубка Рийке, где горячий воздух проходит через холодную решетку.

Трубки Sondhauss и Taconis

Трубка Зондхауса — один из первых генераторов теплового тона; он был обнаружен в стеклодувной промышленности. К одному концу трубки, имеющей комнатную температуру, подсоединена лампочка с горячим воздухом. При продувке холодной трубки возникают акустические колебания трубки. Об этом говорил барон Рэлей в своей «Теории звука». Это устройство не считается настоящим свистком, поскольку колебания затухают по мере выравнивания температур.

Анализируя эту трубку, Рэлей заметил, что если бы тепло было добавлено в точке наибольшей плотности звуковой волны и вычтено в точке наименьшей плотности, вибрация усилилась бы. Другой тепловой эффект называется колебанием Такониса. ^[20] Если трубка из нержавеющей стали имеет одну сторону при комнатной температуре, а другую - в контакте с жидким и сверхтекучим гелием, наблюдаются спонтанные акустические колебания. Опять же, трубка Зондхауса не является настоящим свистком.

Человеческий свисток

Количество и разнообразие свистков, созданных людьми, довольно велико, однако с точки зрения физики человеческий свист был исследован очень мало. Существует три возможных механизма: резонанс Гельмгольца , операция симметричного дырочного тона (монополь) или операция асимметричного краевого тона (диполь).

Уилсон и его коллеги ^[1] смоделировали человеческий свисток, создав цилиндр диаметром 2,04 дюйма (52 мм) с закругленным отверстием на одном конце, через которое подается струя, и другим закругленным отверстием на другом конце того же диаметра и на той же оси. Геометрия была очень похожа на геометрию свистка для чайника. После ряда испытаний на различных скоростях, диаметрах и толщинах отверстий они пришли к выводу, что свист создается резонансом Гельмгольца в объеме цилиндра. В их исследовании было достаточно данных для одного случая, чтобы вычислить числа Струхаля и Рейнольдса. Результаты показаны на рисунке справа.

Число Струхаля было практически постоянным в ограниченном диапазоне скоростей, что предполагает работу с дырочным тоном с обратной связью класса I или класса II. Их работа, как и следовало ожидать, указала на симметричное неустойчивое вихревое течение, но не было упоминания о стадиях. В исследовании Генри Вуда ^{[ нужна ссылка ]}было отмечено, что резонанс Гельмгольца может возникать на малых скоростях. Гибкость рта предполагает, что, хотя механизм обратной связи по дырочному тону весьма вероятен, возможность резонансов Гельмгольца в ротовой полости и асимметричное воздействие краевого тона на зубы считаются возможными.

Листовой свисток

Лист можно использовать как свисток, который может воспроизводить до трех октав. Это популярный инструмент во многих культурах: в Камбодже его называют slek , 木叶 (Mù yè) в Китае, жевательный лист в Австралии и Birkenblatt Blasen в Германии. С помощью высокоскоростной камеры можно увидеть, как лист отрывается от губ, когда игрок дует, и его эластичность возвращает его на губу. Это колебательное движение заставляет его вибрировать, создавая звук. Анализ серии обертонов, сравнивающий гобой и биркенблатт, играющие ноту F2, показывает, что они практически идентичны. ^[21]

Дипольные свистки

В этих свистках неустойчивость течения асимметрична, часто приводит к появлению рядов чередующихся вихрей, а генерация звука связана с колебаниями приложенной силы. Звуковое поле находится настолько близко к дипольному источнику, насколько это позволяет местная геометрия.

Эолийский тон

Устойчивый поток над цилиндром (или подобным объектом) создает вихри и, как следствие, звук. Ранние греки использовали это явление для создания арфы, и этот звук называли эоловым тоном в честь Эола , бога ветра.

Другими примерами этого тона являются свист телефонных проводов, автомобильных радиоантенн, передних решеток некоторых автомобилей и дымовых труб. При очень малых числах Рейнольдса обтекание цилиндра устойчиво, образуя за ним два неподвижных вихря. По мере увеличения скорости течение хотя и ламинарное, но становится неустойчивым, и вихри возникают попеременно .

Гидродинамическая обратная связь (класс I) влияет на образование новых вихрей и оказывает на цилиндр колебательную силу. Поле потока показано на верхнем рисунке справа (создано Гэри Купманом). Теодор фон Карман ^[22] идентифицировал и проанализировал течение за объектами, подобными цилиндру, и с тех пор этот особый поток получил название вихревой улицы Кармана . Винсент Струхаль был первым, кто научно исследовал звук, издаваемый обтеканием твердого цилиндра. При малых числах Рейнольдса тон был чистым, а частота была пропорциональна установившейся скорости потока U и обратно пропорциональна диаметру цилиндра d .

Во многих приложениях часто используется первое уравнение, приведенное ниже. Обзор литературы ^[23] создал рисунок справа для числа Струхаля. При низких числах Рейнольдса число Струхаля возрастает, поскольку инерционные эффекты начинают доминировать, а затем немного затухает при более высоких числах. Второе уравнение ниже лучше всего подходит для данных для 1000 < Re < 100 000 .

{\begin{aligned}{\text{St}}&={\frac {fd}{U}}\approx 0.2;\\{\text{St}}&=0.218\left({\frac {\text{Re}}{1000}}\right)^{-0.042}\end{aligned}}

Удивительно, как часто явления колебательного течения имеют числа Струхаля в этом диапазоне. Для сравнения формы число Струхаля для эллипса составило 0,218, цилиндра — 0,188, квадрата — 0,160 и треугольника — 0,214. Характерный размер - это размер объекта сбоку от потока, а характерная скорость - это скорость набегающего потока.

Второе уравнение предполагает, что число Струхаля является слабой отрицательной функцией числа Рейнольдса. Это говорит о том, что приближение динамического подобия является разумным. Колеблющаяся сила, действующая на цилиндр, является результатом циркуляции потока вокруг него, вызванной попеременным разделением вихрей, как показано на третьем рисунке. Тот факт, что вихри не находятся непосредственно за цилиндром, предполагает, что вектор силы имеет как подъемную силу, так и составляющую сопротивления, что приводит к появлению диполей подъемной силы и сопротивления.

Приблизительный способ связать генерируемый звук с характеристиками потока — это исказить стандартное уравнение сопротивления с помощью возмущений скорости, как показано в верхнем уравнении ниже (измерения подъемной силы для цилиндров обычно недоступны). Верхнее уравнение представляет собой модифицированное уравнение сопротивления, включающее как компонент сопротивления u, так и компонент подъемной силы v , а также площадь поперечного сечения dL , где d — диаметр цилиндра, а w — длина.

{\begin{aligned}F&=F_{d}+F'_{d}+F'_{l}={\frac {C_{d}\rho _{0}}{2}}(U+u'+v')^{2}\,dw\\W_{d}&={\frac {3\pi \rho _{0}}{c_{0}^{3}}}S^{2}U^{6}dwC_{d}^{2}{\overline {\left({\frac {u'}{U}}\right)^{2}}}\\W_{l}&={\frac {3\pi \rho _{0}}{c_{0}^{3}}}S^{2}U^{6}dwC_{d}^{2}{\overline {\left({\frac {v'}{U}}\right)^{2}}}\end{aligned}}

Манипулирование уравнением дает два нижних уравнения для дипольной звуковой мощности как подъемной силы, так и сопротивления. Каждый раз при срыве вихря колебание скорости сопротивления u имеет один и тот же знак, но колебание боковой скорости v имеет противоположные знаки, поскольку вихрь сбрасывается по разные стороны. В результате ожидается, что частота диполя сопротивления будет в два раза выше частоты подъемного диполя.

Филлипс ^[24] обнаружил, что флуктуации поперечной скорости на два порядка превышают продольные, поэтому подъемный диполь находится на 20 дБ выше диполя сопротивления. Он обнаружил, что диполь сопротивления действительно возникает на частоте вдвое большей, чем диполь подъемной силы. На более высоких скоростях разделение вихрей может не коррелировать по всей длине цилиндра, что приводит к появлению множества по существу независимых дипольных источников и снижению звуковой мощности. Нижний рисунок справа показывает коэффициент корреляции как функцию расстояния вдоль цилиндра и взят из работы Эткина и др. изучать. ^{[ нужна ссылка ]}

Задний тон

Пограничный слой на профиле планера ламинарный, а на задней кромке происходит вихреобразование, подобное цилиндру. Звук может быть почти чистым тоном.

На рисунке слева показан спектр третьоктавной полосы, полученный при пролете планера; тон на 15 дБ выше широкополосного звука. Скорость самолета U составляла 51 м/с (170 футов/с), а частота — около 1400 Гц.

На основании числа Струхаля, равного 0,20, было рассчитано, что характерный размер δ составляет около 0,25 дюйма (6,4 мм); толщина пограничного слоя. На задней кромке за счет действующей на нее флуктуирующей силы создавалось дипольное звуковое поле.

На более высоких скоростях самолетов с двигателем пограничный слой на аэродинамическом профиле является турбулентным, и наблюдаются более сложные схемы образования вихрей. Поскольку это трудно измерить в полете, Хейден ^[25] провел статические испытания.

На рисунке справа показан пример. Течение в пограничном слое создавалось с обеих сторон тонкой жесткой плоской пластины, оканчивающейся квадратной задней кромкой. Обратите внимание на почти чистый тон на частоте 2000 Гц с числом Струхаля 0,21, выступающий над турбулентным звуковым спектром. И снова появляется магическое число Струхаля. Характерной скоростью была средняя скорость U струи, а характерным размером была выбрана толщина задней кромки t . Лучшим характерным размером была бы толщина пограничного слоя, но, к счастью, эти два измерения были почти одинаковыми. Измеренное звуковое поле было явно дипольным (слегка измененным наличием пластины).

На нижнем рисунке справа показано несколько спектров турбулентного звука, измеренных на различных скоростях. ^[26] Частоты представляли собой число Струхаля, масштабированное с помощью U , а уровни звука были масштабированы с помощью правила дипольной звуковой мощности U. ⁶ в диапазоне скоростей от 3 до 1. Согласование данных было довольно хорошим, подтверждая динамическое подобие и дипольную модель. Небольшое расхождение в перекрытии уровней и частот позволяет предположить, что как безразмерная сила, так и число Струхаля слабо зависели от числа Рейнольдса.

Еще одним характерным размером является хорда профиля. В этих испытаниях ширина струи была достаточной, чтобы обеспечить равномерное распространение вихря поперек нее. На профиле крыла корреляционная длина будет меньше размаха крыла, что приведет к появлению нескольких независимых диполей, расположенных по бокам. Звуковая мощность несколько уменьшится. Поскольку модель диполя основана на скорости изменения силы во времени, уменьшение звуковой мощности может быть достигнуто за счет уменьшения этой скорости. Одним из возможных способов было бы постепенное пространственное обнаружение друг друга противоположными сторонами поверхности до задней кромки и, таким образом, снижение скорости на кромке. Это может быть сделано с помощью секции градуированных пористых или гибких материалов.

Свисток для циркулярной пилы

Краевой тон возникает, когда струя падает на неподвижную поверхность. Звук заднего фронта возникает, когда внешний поток проходит через задний фронт. Существует свист, который представляет собой комбинацию пограничного и заднего тона и может быть назван сигналом пробуждения . Он возникает во вращающихся циркулярных пилах на холостом ходу и может быть назван свистом циркулярной пилы . В условиях нагрузки играет роль вибрация лезвия, которая здесь не рассматривается.

Было проведено несколько исследований фундаментальных механизмов генерации звука этого свистка. ^[27]^[28]^[29]^[30]^[31]

Чертеж типичной конструкции лопасти показан на рисунке справа. Исследования показали, что звуковое поле является дипольным с первичной осью, перпендикулярной плоскости лопасти. Источниками являются колебательные силы, действующие на каждое режущее лезвие. Бис определил, что характеристической скоростью является скорость лезвия RΩ , а характерным размером является площадь зуба. Другие исследователи использовали толщину лезвия в качестве характерного размера. Чо и Мот обнаружили, что число Струхаля St = fh / U находится в диапазоне от 0,1 до 0,2, где h — толщина лезвия. Поблете и др. обнаружили числа Струхаля между 0,12 и 0,18. Если тон края имеет значение, возможно, характерным размером должен быть зазор между лезвиями.

Исследователи пришли к выводу, что колеблющаяся сила пропорциональна U. ², но оказалось, что звуковая мощность варьируется от U ^4.5 к тебе ^6.0. Если полоса измерения широка, а расстояние измерения находится за пределами ближнего поля, существуют два динамических фактора (число Струхаля и безразмерная сила), которые могут привести к тому, что показатель степени будет меньше 6. Данные дельтаметра и тона дырок показывают Число Струхаля представляет собой слабую отрицательную функцию числа Рейнольдса, возведенного в квадрат в уравнении звуковой мощности. Это приведет к уменьшению показателя скорости. Однако этот фактор вряд ли может объяснить значительное снижение показателя степени.

Геометрия лопасти сильно менялась в ходе испытаний, поэтому, вероятно, основным фактором является отрицательная зависимость безразмерной силы от числа Рейнольдса. Этот свисток имеет две особенности, которые отличают его от других описанных здесь свистков. Во-первых, существует множество этих дипольных источников, расположенных по периферии, которые, скорее всего, излучают одну и ту же частоту, но некогерентно. Во-вторых, движение лопастей создает устойчивое, но вращающееся поле давления на каждой лопасти. Вращающаяся постоянная сила создает вращающееся дипольное поле, которое оказывает влияние на геометрическое ближнее поле. Обратная связь относится к классу I (гидродинамическая), и нет никаких признаков возникновения других стадий, кроме стадии 1.

Мелодия звонка

Слово «кольцо» здесь относится к тороидальной форме. Поток из круглого отверстия, падающий на тороидальное кольцо того же диаметра, что и отверстие, приведет к появлению звука; это называется мелодия звонка . Он аналогичен описанному выше дырочному тону, за исключением того, что из-за замены пластины кольцом происходит фундаментальное изменение результирующего звукового поля. Небольшие возмущения в кольце возвращаются к отверстию и усиливаются нестабильностью потока (класс I). Неустойчивый поток создает набор симметричных (кольцевых) вихрей, которые впоследствии сталкиваются с физическим кольцом.

Прохождение вихря кольцом схематически показано на рисунке справа в три этапа. Векторы потока на рисунке лишь указывают на направление.

Когда два вихря равноудалены от кольца, один находится за его пределами, а другой приближается, чистая циркуляция вокруг кольца равна нулю; нулевая точка колебаний потока. Каждый вихрь создает круговое (кольцевое) поле потока, ось которого слегка отклоняется от вертикали при прохождении. Из рисунка видно, что основная составляющая силы, действующей на физическое кольцо, направлена по направлению струйного течения. Если вихрь представляет собой настоящее кольцо (все части находятся в фазе), создается дипольное звуковое поле, направленное вдоль оси струи.

Рисунок также предполагает наличие латеральной составляющей силы, которую можно интерпретировать только как слабый радиальный диполь. Были проведены эксперименты с мелодией звонка. ^[4] Нижний рисунок справа показывает связь частоты с числом Рейнольдса. Если бы вместо частоты было отображено число Струхаля, это показало бы, что контуры были достаточно постоянными, подобно контурам дырочного тона. Внимательное изучение данных на рисунке показало небольшую отрицательную зависимость числа Струхаля от числа Рейнольдса.

Оказывается, этот свисток имеет всего две ступени. Звуковое поле было измерено и четко обозначило диполь, ось которого совпадала с осью струи. Поскольку рядом с источником не было отражающих поверхностей, данные также указывали на существование более слабой радиальной дипольной компоненты. Такое поле может существовать только в том случае, если в удаленной точке между каждым из компонентов силы существует временная задержка.

Вихревой свисток

Когда закрученный поток внутри трубы достигает выхода, он может стать нестабильным. Пример исходной системы показан на рисунке слева. Неустойчивость возникает при наличии обратного течения на оси.

Сама ось вращения прецессирует вокруг оси трубы, что приводит к возникновению вращающей силы на выходе трубы и образованию вращающегося дипольного звукового поля. Исследования этого свистка ^[32]^[33] показали, что динамическое подобие, основанное на диаметре трубы d как характерном масштабе длины и средней скорости потока на входе U как характерной скорости, не было достигнуто, как показано на нижнем рисунке справа. Более правильной скоростью была бы та характеристика вихря fd , где f — частота прецессии (и звука), основанная на числе Россби . Чтобы проверить актуальность этой новой характеристики скорости, скорость потока была увеличена, а также измерены частота и уровень звука. Используя дипольную модель, было обнаружено, что рассчитанная сила почти пропорциональна ( fd ) ², подтверждая правильность новой характеристики скорости.

Измерения показали, что вихревой свист создавался вращающимся асимметричным вихрем, который создавал вращающийся вектор силы в плоскости выхода и вращающееся дипольное звуковое поле. Было показано, что явление вихревой неустойчивости имеет место и в других ситуациях. ^[34] Одним из них был отрыв потока на верхней стороне дельтовидных профилей высокоскоростных самолетов ( «Конкорд» ). Угол атаки передней кромки привел к возникновению закрученного потока, который стал неустойчивым. Другой — поток внутри циклонных сепараторов; там закрученный поток возникает в кольцевой области между двумя трубками. Поток меняет направление на закрытом конце внешней трубки и выходит через внутреннюю трубку. При определенных условиях поток в области разворота становится нестабильным, что приводит к возникновению периодической вращающей силы на внешней трубке.

Периодическая вибрация циклонного сепаратора будет указывать на нестабильность вихря. В больших центробежных вентиляторах иногда используются радиальные впускные лопасти, которые можно вращать, чтобы контролировать поток в вентилятор; они создают закрученный поток. При близком отключении, когда завихрение очень сильное, происходит срыв вращающихся лопастей вентилятора. Хотя это и не исследовано, весьма вероятно, что причиной является вихревая нестабильность. Обратная связь явно гидродинамическая (класс I), и нет никаких признаков того, что происходит более одной стадии.

Вихревой счетчик

Причиной отсутствия динамического подобия считался способ создания закрутки в вихревом свистке, поэтому закрутку создавали в трубе с сужением, имеющим завихрительные лопасти с последующим расширением для создания необходимого осевого противотока. Это был вихревой свист в трубе. Измерения, выполненные при такой геометрии, показаны на рисунке справа. Как видно, динамическое подобие было достигнуто как с воздухом, так и с водой. Этот свисток стал расходомером, названным вихревым измерителем . Его точность не уступает по точности измерителям вихреобразования, описанным выше, но имеет более высокий перепад давления. Обратная связь гидродинамическая (класс I), обнаружена только одна ступень.

Краевой тон

Когда прямоугольная струя падает на объект с острыми краями, например, на клин, может возникнуть петля обратной связи, что приводит к почти чистому звуку. На рисунке справа схематически показано движение двух вихрей при прохождении клина. Эта простая диаграмма предполагает, что к клину приложена сила, угол которой меняется по мере прохождения вихрей.

Как обнаружено в эоловом тоне, вертикальная составляющая (подъем) велика и приводит к дипольному звуковому полю на клине (показано на нижнем рисунке) и гораздо более слабой горизонтальной составляющей (сопротивление) на удвоенной частоте (не показано). ). Компонент сопротивления может выступать в качестве движущей силы музыкальных инструментов (обсуждается ниже). Основополагающее исследование Пауэлла ^[35] этого явления выявило многие детали явления краевого тона. Он показал, что этот свисток имеет три ступени, а петля обратной связи гидродинамическая (класс I). Полуэмпирическое уравнение для частоты, разработанное Керлом: ^[36] при преобразовании в число Струхаля

{\text{St}}_{n}={\frac {fh}{U}}=\left({\frac {4n+1}{8}}-{\frac {h}{60d}}\right).

Это уравнение, применимое для h / d > 10, показывает среднюю скорость U струи у отверстия как характерную скорость, а расстояние h от отверстия до края как характерный размер. Целое число n представляет различные режимы вихря. Это также предполагает, что динамическое подобие достигается в первом приближении; одно отклонение состоит в том, что характеристической скоростью должна быть скорость у клина, которая меньше скорости у отверстия. Вероятен слабый отрицательный эффект числа Рейнольдса. Ширина отверстия d также имеет некоторое влияние; это связано с размером вихря и латеральной корреляцией процесса срыва.

Наличие дипольного звукового поля и периодической силы, пропорциональной U ² было подтверждено Пауэллом. Численное моделирование краевого тона и обширные ссылки можно найти в отчете НАСА. ^[37] Нижний рисунок справа можно назвать сигналом пробуждения . Если предпочтительные частоты нестабильности заднего фронта совпадают с предпочтительными частотами тона свободного фронта, должен возникнуть более сильный дипольный звук. Похоже, что никаких исследований по этой конфигурации не проводилось.

Тон мелкой полости

Исследование звука, создаваемого обтеканием полостей на высокой скорости, хорошо финансировалось федеральным правительством, поэтому было приложено немало усилий. Проблема связана с обтеканием полостей самолета в полете, таких как бомбовые отсеки или ниши колес. Обтекание полости на поверхности может привести к возбуждению петли обратной связи и почти чистым звукам. В отличие от тона края, отмеченного выше, край полости обычно имеет квадратную форму, но также может быть краем как часть тонкой структурной оболочки. Полости можно разделить на мелкие и глубокие , с той разницей, что для глубоких полостей управляющим может быть канал обратной связи класса III (акустический). Здесь рассматриваются неглубокие полости, в которых длина полости L больше глубины D полости .

При больших скоростях U течение является турбулентным, а в некоторых исследованиях скорость может быть сверхзвуковой, а уровень генерируемого звука может быть достаточно высоким. Одно исследование ^[38] показал, что в неглубокой полости могут возникать несколько мод колебаний (стадий); числом вихрей на расстоянии L. моды связаны с Для более коротких полостей и меньших чисел Маха существует режим сдвигового слоя , а для более длинных полостей и более высоких чисел Маха существует режим следа . Режим сдвигового слоя хорошо характеризуется процессом обратной связи, описанным Росситером. Вместо этого режим следа характеризуется крупномасштабным вихревым выбросом с числом Струхаля, не зависящим от числа Маха. Для этих данных существует эмпирическое уравнение; это называется формулой Росситера .

Ли и другие ^[39]^[40] показали это в форме числа Струхаля как

{\text{St}}_{n}={\frac {f_{n}L}{U}}={\frac {n-\beta }{U\left({\frac {1}{c_{0}}}+{\frac {1}{u_{v}}}\right)}}

Термин в скобках включает в себя две скорости контура обратной связи: скорость нисходящего потока — это скорость вихрей u , а скорость восходящего потока — скорость звука c ₀ . Различные режимы описываются целым числом n с эмпирической константой задержки β (около 0,25). Целое число n тесно связано с количеством вихрей на пути к краю. Из теневых изображений ясно, что источником звука является колебательная сила вблизи нижнего края. Поскольку число Маха потока может быть значительным, рефракция затрудняет определение большой оси дипольного звукового поля. Предпочтительные частоты в неглубоких полостях отличаются от частот краевого тона.

Полицейский свисток

Его обычно используют для описания свистков, подобных тем, которые используются полицией в Америке и других странах. Существует ряд свистков, которые действуют так же, как полицейский свисток, а также ряд свистков, используемых полицией в других местах, которые действуют не так же, как полицейский свисток. Лондонская столичная полиция использует линейный свисток, больше похожий на небольшой диктофон. Полицейские свистки обычно используются судьями и судьями на спортивных мероприятиях.

Разрез обыкновенного свистка показан на рисунке справа. Полость представляет собой цилиндр закрытого типа ( 3 ⁄ дюйма диаметром (19 мм), но с осью цилиндра, расположенной сбоку от оси струи. Отверстие Ширина 1 ⁄ 16 дюйма (1,6 мм), острый край На расстоянии 1 ⁄ дюйма (6,4 мм) от форсуночного отверстия. При слабом продувании звук преимущественно широкополосный, со слабым тоном. При более сильном продувке устанавливается сильный тон около 2800 Гц, а соседние полосы понижаются как минимум на 20 дБ. Если свистнуть еще сильнее, уровень тона увеличится, а частота увеличится лишь незначительно, что предполагает гидродинамическую обратную связь I класса и работу только на I ступени.

Как представляется, никаких подробных исследований по использованию полицейских свистков не проводилось. Учитывая упомянутый выше краевой тон, можно было бы ожидать нескольких скачков частоты, но ничего не происходит. Это говорит о том, что если в нестабильной струе существует несколько вихрей, они не контролируют ее.

Схема справа предлагает правдоподобное объяснение работы свистка. Внутри полости находится нецентральный вихрь. На верхнем рисунке центр вихря находится вблизи струи; течение в близлежащей полости медленнее, а давление меньше атмосферного, поэтому струя направляется в полость. Когда струя движется к полости, внутреннему вертикальному потоку придается дополнительная тяга, который затем вращается вокруг края и обратно. В этот момент поток в полости и местное давление достаточны, чтобы заставить струю отойти от полости.

Внутренний вихрь такого типа мог бы объяснить, почему не происходит скачков частоты. Поскольку избыток жидкости в полости должен быть удален, боковое движение струи должно быть значительно больше, чем при краевом тоне; скорее всего, это причина высокого уровня звука. Поток через край приводит к возникновению приложенной силы и звукового поля, подобного диполю. Характеристическая скорость должна быть скоростью выхода U. струи соответствовать диаметру полости D. Характерный размер должен

Частота звука тесно связана со скоростью вращения вихря полости. При частоте около 2800 Гц внутренняя скорость вращения должна быть очень высокой. Вполне вероятно, что число Россби U /( fD ) будет ценным динамическим числом подобия. похожа Трубка боцмана на полицейский свисток, за исключением того, что полость имеет сферическую форму, что создает более сложный вихрь.

Гороховый свисток/судейский свисток

Гороховый свисток конструктивно идентичен «полицейскому свистку», но в камере находится небольшой шарик, известный как горох, но обычно из такого материала, как пластик или твердая резина. При выдувании горошина хаотично движется в камере, прерывая и модулируя поток воздуха, создавая типичный эффект трелей/визжа. Такие свистки традиционно используются судьями футбольных ассоциаций и судей других игр.

Самба свистит

Подобно гороховым свисткам, свистки для самбы имеют небольшой шарик или дюбель для создания такого же звука, но часто также имеют два удлинителя по обе стороны камеры. Ни один, один или оба из них могут быть заблокированы для создания «трехцветного» эффекта. Апито де самба — традиционный португальский свисток для самбы.

Свисток Левавассера

Этот свисток, по сути, представляет собой полицейский свисток, превращенный в тор, что увеличивает его звуковой потенциал. Поперечное сечение середины свистка показано на рисунке справа.

Кольцевой канал несет жидкость, которая создает кольцевую струю. Струя попадает в кольцо с острым концом и двумя тороидальными полостями с каждой стороны. В патенте Левавассера ^[41] После кольцевого отверстия добавляется конструкция, которая действует как соединительный рупор и направляет звук. Издаваемый звук очень интенсивный. Похоже, что не проводилось никаких научных исследований для выяснения подробных механизмов обратной связи его работы, хотя ясно, что этот свисток имеет механизм обратной связи класса I, аналогичный полицейскому свистку.

Характеристическая скорость U соответствует скорости кольцевой струи. Характерный размер D представляет собой диаметр полости, и оказывается, что обе полости имеют одинаковые размеры. Опять же, число Россби VU /( fD ), вероятно, будет важным динамическим числом, поскольку работа внутренней полости должна быть аналогична работе полицейского свистка. Вполне вероятно, что вихрь во внешней полости находится в противофазе с внутренней полостью, что усиливает смещение струи и, следовательно, выход звука.

Визговый тон

Сильные звуки могут возникать как в прямоугольных, так и в круглых струях, когда степень давления превышает критическую и поток на выходе становится сверхзвуковым, что приводит к последовательности повторяющихся ударных ячеек. Эти клетки можно увидеть в выхлопах ракет или самолетов, работающих на форсажной камере. Как и дозвуковые струи, эти течения могут быть неустойчивыми.

В прямоугольной струе нестабильность может проявляться в виде асимметричных искажений ячеек. Асимметрия отправляет волны обратно в сопло, что создает петлю обратной связи класса III и сильное периодическое дипольное звуковое поле; это называется визговый тон . Пауэлл ^[42]^[43] впервые описал это явление, и из-за его применения в военных самолетах и потенциальной усталости конструкции была проделана большая последующая работа. Звуковое поле достаточно интенсивно, чтобы появиться на теневой диаграмме, как показано на рисунке справа (от М.Г. Дэвиса ) для прямоугольной сверхзвуковой струи. Дипольная природа источника очевидна по обращению фазы по обе стороны струи. Существует боковое движение ударных ячеек, которое придает диполю его ось.

Сверхзвуковые потоки могут быть весьма сложными, и существуют некоторые предварительные объяснения. ^[39]^[44] Как и в случае с мелодиями и звонками, эти форсунки могут быть чувствительны к местным звукоотражающим поверхностям.

Характеристической скоростью U является скорость в выходной плоскости, а характерным размером L является ширина сопла, которой пропорциональны размеры ячейки. Круглые сверхзвуковые струи также издают визг. Однако в этом случае могут быть три режима движения: симметричный (тороидальный), асимметричный (извилистый) и винтовой. ^[45]^[46]^[47] Эти свистки не похожи на другие, перечисленные выше; звук генерируется без взаимодействия с твердым телом; это действительно аэродинамический свисток.

Гидравлические генераторы

Эти устройства представляют собой свистки, которые не излучают звук, но все же являются аэродинамическими свистками. На верхнем рисунке справа показано базовое устройство одного варианта устройства. Круг слева — источник жидкости (воздух или жидкость). Образуется струя, которая уходит либо в верхний, либо в нижний канал.

Черные линии — это пути обратной связи. Если жидкость находится в нижнем канале, некоторое количество жидкости возвращается к источнику струи через черную трубку и выталкивает струю в верхний канал.

Эти устройства получили значительное развитие от переключателей цепей, невосприимчивых к электромагнитным импульсам, до более современных применений.

Уникальность этого свистка по сравнению с другими описанными заключается в том, что длину пути обратной связи можно выбирать произвольно. Хотя каналы разделены клиновидной формой, использование краевых тонов предотвращается благодаря эффекту Коанды . На втором рисунке справа показаны результаты одного исследования. ^[48] что указывает на постоянное число Струхаля с числом Рейнольдса. Данные были нормализованы до эталонного значения.

В другом исследовании ^[49] один набор их частотных данных был пересчитан с точки зрения числа Струхаля, и было обнаружено, что оно медленно растет, а затем становится постоянным в диапазоне скоростей потока. Ким ^[50] обнаружили аналогичный результат: число Струхаля увеличивалось вместе с числом Рейнольдса, а затем оставалось постоянным, как показано на нижнем рисунке справа. Еще одна уникальность этого свистка заключается в том, что обратная связь достаточно сильна, чтобы струя отклонялась в сторону тела, а не зависела от развития вихрей нестабильности потока для управления ею. Геометрия устройства предполагает, что это по сути дипольный источник, работающий в I ступени с I класса (гидродинамической) обратной связью.

Монополь-дипольные свистки

Существует ряд свистков, обладающих характеристиками как монопольных, так и дипольных источников звука. В некоторых свистках, описанных ниже, источником возбуждения является диполь (обычно краевой тон), а отвечающим источником является монополь (обычно трубка или полость вблизи диполя).

Принципиальное отличие этих свистков от описанных выше состоит в том, что теперь имеется два набора характеристических переменных. движущего источника характерная скорость равна U , а характерный размер равен L1 _Для . Для реагирующего источника характерная скорость равна c ₀ , а характерный размер равен L ₂ , обычно это скорректированная глубина полости или длина трубки. Безразмерными дескрипторами каждого из них являются гидромеханическое число Струхаля и акустическое число Струхаля. Связь между этими двумя числами заключается в общности частоты.

Кувшинный свисток

Если дуть через край кувшина или бутылки, можно создать почти чистый низкочастотный звук. Движущей силой является поток через край кувшина, поэтому можно ожидать дипольного звукового поля краевого тона. В этом случае кривизна и закругленность края делают сильный тон края маловероятным. Любая периодичность на краю, скорее всего, заглушена обратной связью III класса от объема кувшина. Нестационарный краевой поток создает классический отклик резонатора Гельмгольца , в котором внутренняя геометрия и горлышко кувшина определяют результирующую частоту. Резонансное уравнение: ^[51]

{\begin{aligned}\cot(kL)&={\frac {A_{\text{c}}(L_{\text{o}}+\delta _{\text{e}}+\delta _{\text{i}})}{A_{\text{o}}}}kL\\kL&=2\pi {\frac {fL}{c_{0}}}=2\pi {\text{St}}\end{aligned}}

Это трансцендентное уравнение, где Ac _L. площадь поперечного сечения цилиндрической полости — глубиной A _o представляет собой площадь круглого отверстия глубиной L _o , δ _e представляет собой поправку на внешний конец, δ _i представляет собой поправку на внутренний конец и kL представляет собой число Гельмгольца (акустическое число Струхаля с добавлением 2 $π$ ). Цилиндрическая полость глубиной 9 дюймов (230 мм) и диаметром 4,25 дюйма (108 мм) была соединена с круглым отверстием диаметром 1,375 дюйма (34,9 мм) и глубиной 1,375 дюйма (34,9 мм). ^[52] Измеренная частота была близка к 140 Гц. Если бы резонатор действовал как четвертьволновой резонатор, частота была бы 377 Гц; явно не продольный резонанс.

В приведенном выше уравнении указана частота 146 Гц, а в уравнении Нильсена ^[53] указано 138 Гц. Очевидно, что свист приводился в движение резонансом полости. Это пример свистка, работающего в режиме краевого тона, но в результате получается монопольное звуковое поле.

Глубокий тон

Течение над полостью, которая считается глубокой, может создавать свист, аналогичный свисту над неглубокими полостями. Глубокую обычно отличают от мелкой тем, что глубина полости больше ширины. Были изучены две геометрии. Первая геометрия представляет собой поток снаружи полости, например, в самолете. ^[54]^[55]^[56]^[40]

Существует два характерных размера (ширина полости L , связанная с развитием вихря, и глубина полости D , связанная с акустическим откликом). Имеются две характерные скорости (скорость потока U , связанная с развитием вихря, и скорость звука c0 _, связанная с реакцией каверны). Было обнаружено, что обратная связь относится к классу III, а числа Струхаля в диапазоне от 0,3 до 0,4 связаны с одним вихревым рисунком (стадия I) через зазор, а числа Струхаля в диапазоне от 0,6 до 0,9 связаны с двумя вихрями через зазор. (II этап).

Вторая геометрия – течение в канале с боковым ответвлением. Селамет и его коллеги ^[57]^[58]^[59] провели обширные исследования свистовых явлений в каналах с закрытыми на одном конце боковыми ответвлениями. Для этих исследований глубина полости составляла L , а D — диаметр боковой ветви. Жидко -механические и акустические числа Струхаля составили:

{\begin{aligned}{\text{St}}&={\frac {fD}{U}}\\{\text{St}}_{\text{a}}&={\frac {fL_{1}}{c_{0}}}={\frac {2n+1}{4}}\\L_{1}&=L\left(1+\beta {\frac {D}{L}}\right)\end{aligned}}

произвольная константа β Для представления импеданса в месте соединения боковой ветви с воздуховодом использовалась . n было целым числом, представляющим номер этапа. Они отметили, что число Струхаля оставалось постоянным при увеличении скорости.

Орган

Орган — еще один пример потенциально дипольного источника звука, работающего как монопольный источник. Воздушная струя направляется на острую кромку, создавая колебания потока, как в кромочном тоне. Край является частью обычно цилиндрической трубки L. длиной Пример показан на рисунке справа. ^{[ где? ]} Нестабильная струя поочередно гонит жидкость в трубку и наружу. Линии тока явно искажены по сравнению с линиями свободного края. Напротив источника находится точка застоя. Пунктирные линии, окрашенные в красный цвет, представляют собой наиболее сильно измененные участки. Красные линии тока в трубке теперь дополняются колебательным потоком в трубке, суперпозицией резистивного и реактивного дипольного потока и резистивного акустического потока.

Длина трубки определяет, оказывает ли акустическое давление или скорость трубки доминирующее влияние на частоту трубки. Простые модели резонанса орган-труба основаны на резонансе открытой-открытой трубы ( λ = L /2), но необходимо внести поправки, чтобы принять во внимание, что один конец трубы излучает в окружающую среду, а другой излучает через щель струйным потоком. Бёлкес и Хоффманн ^[60] провели измерения торцевой поправки для трубок «открыто-открыто» и получили соотношение δ = 0,33 D . Это не может быть точным, поскольку приводной конец не открыт.

Излучение ± импеданс на ведущем конце должно привести трубку к состоянию λ /4, еще больше снижая частоту. Поскольку существуют две связанные системы, то и шкалы характеристик две. трубчатого компонента характерный размер равен L , а характерная скорость равна c0 _Для . отверстия до края Для компонента краевого тона характерным размером является расстояние h , а характеристической скоростью является скорость струи U. от Казалось бы, максимальный коэффициент усиления системы будет иметь место, когда предпочтительная частота трубы соответствует предпочтительной частоте краевого тона с подходящей фазой. Эта зависимость, выраженная через числа Струхаля, имеет вид:

{\begin{aligned}{\text{St}}_{\text{c}}&={\frac {fL_{1}}{c_{0}}}&&{\text{St}}_{e}={\frac {fh}{U}}\\{\text{St}}_{\text{c}}&={\text{St}}_{\text{e}}{\frac {L_{1}}{h}}M\end{aligned}}

Если динамическое сходство сохраняется для обоих резонансов, последнее уравнение показывает, как масштабируются органные трубы. За кажущейся простотой уравнения скрываются важные переменные факторы, такие как эффективная длина трубы L ₁ = L+ δ ₁ + δ ₂ , где δ ₁ — поправка для открытого конца, а δ ₂ — поправка для конца вблизи струи. Скорость возмущения струи (вихря) от отверстия до края будет варьироваться в зависимости от средней скорости U , расстояния до края h и ширины щели d , как указано в разделе «Тон грани» .

Соотношение Струхаля предполагает, что в первом приближении важны число Маха струи и отношение эффективной длины трубы к краевому расстоянию. При нормальной работе трубы будет использоваться монопольный источник звука на ступени I с обратной связью класса III.

Флейты, блокфлейты и пикколо

Ряд музыкальных инструментов, кроме органа, основаны на явлении краевого тона , наиболее распространенными из которых являются флейта, пикколо (уменьшенная версия флейты) и блокфлейта. На флейту можно дуть сбоку от инструмента или на конце, как и другие. На рисунке изображена родная флейта с выдувным концом.

Все они подвержены скачкам частоты при чрезмерном раздувании, что указывает на связь диполь-монополь. Аспекты монополя относительно фиксированы. Характерный размер L ₂ трубки фиксирован; характеристическая скорость c ₀ фиксирована. Эффективная длина трубки фиксирована, поскольку импедансы излучения на каждом конце фиксированы. Однако, в отличие от органа, эти инструменты имеют боковые порты для изменения резонансной частоты и, следовательно, акустического числа Струхаля.

Дипольные аспекты также относительно фиксированы. Размер отверстия струи и расстояние h до края фиксированы. Хотя скорость струи U может меняться, гидромеханическое число Струхаля относительно постоянно и обычно работает на стадии I. Когда имеется фазово-когерентное усиление двух аспектов, они работают как монопольные источники класса III. Эффективность излучения монополя значительно выше, чем у диполя, поэтому наблюдается дипольная картина. Детали усиления системы и взаимодействия между этими двумя динамическими системами еще полностью не раскрыты. То, что они смогли добиться правильных размеров и положения отверстий для данной банкноты без научных измерительных инструментов, является свидетельством мастерства первых производителей инструментов.

См. также

Ссылки

^ Jump up to: ^а ^б Уилсон, штат Калифорния; Бобры, ГС; ДеКостер, Массачусетс; Хольгер, ДК; Регенфусс, доктор медицины (1971). «Опыты по гидромеханике свиста». Журнал Акустического общества Америки . 50 (1Б). Акустическое общество Америки (ASA): 366–372. Бибкод : 1971ASAJ...50..366W . дои : 10.1121/1.1912641 . ISSN 0001-4966 .
^ Чано, Роберт К. (январь 1970 г.). «Аэродинамические свистки» . Научный американец . 222 (1): 40–47. Бибкод : 1970SciAm.222a..40C . doi : 10.1038/scientificamerican0170-40 .
^ Чано, Р.К., докторская диссертация, Калифорнийский университет, Лос-Анджелес, 1960.
^ Jump up to: ^а ^б Чано, Колорадо; Пауэлл, Алан (1965). «Некоторые эксперименты относительно отверстия и рингтона» . Журнал Акустического общества Америки . 37 (5). Акустическое общество Америки (ASA): 902–911. Бибкод : 1965ASAJ...37..902C . дои : 10.1121/1.1909476 . ISSN 0001-4966 .
^ Генривуд, Р.Х.; Агарвал, А. (2013). «Аэроакустика парового котла». Физика жидкостей . 25 (10). Издательство АИП: 107101–107101–23. Бибкод : 2013PhFl...25j7101H . дои : 10.1063/1.4821782 . ISSN 1070-6631 .
^ Стратт, Дж. В. Барон Рэлей, Теория звука, MacMillan and Co., 1877.
^ «Тентерфилдский лисий свисток — информационный бюллетень» .
^ Накибоглу, Гюнеш; Руденко, Олексис; Хиршберг, Авраам (2012). «Аэроакустика качающейся гофрированной трубы: голос дракона» . Журнал Акустического общества Америки . 131 (1). Акустическое общество Америки (ASA): 749–765. Бибкод : 2012 ЧЕТВЕРГ..131..749N . дои : 10.1121/1.3651245 . ISSN 0001-4966 . ПМИД 22280698 .
^ Раджавель, Б.; Прасад, МГ (1 июля 2014 г.). «Параметрические исследования акустики гофрированных труб с использованием моделирования больших вихрей (LES)». Инженерный журнал по контролю шума . 62 (4). Институт техники контроля шума (INCE): 218–231. дои : 10.3397/1/376222 . ISSN 0736-2501 .
^ Лиза Р., Тейлор, МЭ, «Экспериментальное исследование акустических характеристик гофрированных трубок», Лаборатория контроля шума и вибрации, Технологический институт Стивенса, Диссертация, 1994.
^ Картик, Б.; Чакраварти, СР; Суджит, Род-Айленд (2008). «Механизм возбуждения трубного тона потоком через отверстие в воздуховоде». Международный журнал аэроакустики . 7 (3–4). Публикации SAGE: 321–347. дои : 10.1260/1475-472x.7.3.321 . ISSN 1475-472X . S2CID 120954769 .
^ Андерсон, ABC (1952). «Зависимость частоты пфейфентона (трубного тона) от длины трубы, диаметра отверстия и давления нагнетания газа». Журнал Акустического общества Америки . 24 (6). Акустическое общество Америки (ASA): 675–681. Бибкод : 1952ASAJ...24..675A . дои : 10.1121/1.1906955 . ISSN 0001-4966 .
^ Андерсон, ABC (1953). «Число круглого отверстия, описывающее зависимость первичной частоты Пфейфентона от перепада давления, плотности газа и геометрии отверстия». Журнал Акустического общества Америки . 25 (4). Акустическое общество Америки (ASA): 626–631. Бибкод : 1953ASAJ...25..626A . дои : 10.1121/1.1907154 . ISSN 0001-4966 .
^ Андерсон, ABC (1955). «Структура и скорость периодического вихрево-кольцевого режима течения первичной струи Пфейфентона (Трубного тона)». Журнал Акустического общества Америки . 27 (6). Акустическое общество Америки (ASA): 1048–1053. Бибкод : 1955ASAJ...27.1048A . дои : 10.1121/1.1908112 . ISSN 0001-4966 .
^ Хартманн, июль (1 декабря 1922 г.). «О новом методе генерации звуковых волн» . Физический обзор . 20 (6). Американское физическое общество (APS): 719–727. Бибкод : 1922PhRv...20..719H . дои : 10.1103/physrev.20.719 . ISSN 0031-899X .
^ Раман, Ганеша; Сринивасан, К. (2009). «Резонансная трубка с приводом: от открытия Хартмана до современных приложений активного управления потоком». Прогресс аэрокосмических наук . 45 (4–5). Эльзевир Б.В.: 97–123. Бибкод : 2009ПрАэС..45...97Р . doi : 10.1016/j.paerosci.2009.05.001 . ISSN 0376-0421 .
^ Брун, Э.; Буше, RMG (1957). «Исследование акустического воздушно-реактивного генератора: новая разработка». Журнал Акустического общества Америки . 29 (5). Акустическое общество Америки (ASA): 573–583. Бибкод : 1957ASAJ...29..573B . дои : 10.1121/1.1908969 . ISSN 0001-4966 .
^ Савой, Л.Е., «Эксперименты с акустическим генератором Хартмана», Engineering, 170, 99–100, 136–138 (1950).
^ Матвеев К., «Термоакустические неустойчивости в трубке Рийке: эксперименты и моделирование». Диссертация, Калифорнийский институт. Тех., 2003.
^ Бакхаус, С., Свифт, Г., «Новые разновидности термоакустических двигателей», 9-й Международный конгресс по звуку и вибрации, 2002.
^ «Веет березовый лист в Гарце – Музыкальное дело Саксония-Анхальт» (на немецком языке) . Проверено 5 августа 2021 г.
^ фон Карман, Т. «Аэродинамика», McGraw-Hill, 1963.
^ Эткин, Б., Рибнер, Х. «Канадские исследования аэродинамического шума», Обзор 13, Институт физики, Univ. Торонто, 1958 год.
^ Филлипс, О.М. (1956). «Интенсивность эоловых тонов». Журнал механики жидкости . 1 (6). Издательство Кембриджского университета (CUP): 607–624. Бибкод : 1956JFM.....1..607P . дои : 10.1017/s0022112056000408 . ISSN 0022-1120 . S2CID 120551027 .
^ Хайден, Р.Э., Фокс, Х.Л., Чано, Р.К. «Некоторые факторы, влияющие на излучение от взаимодействия потока с краями конечных поверхностей», NASA CR-145073, 1976.
^ Рщевкин С.Н., «Теория звука», The MacMillan Company, 1963.
^ Бис, Д.А. (1992). «Аэродинамический шум циркулярной пилы». Журнал звука и вибрации . 154 (3). Эльзевир Б.В.: 495–513. Бибкод : 1992JSV...154..495B . дои : 10.1016/0022-460x(92)90782-s . ISSN 0022-460X .
^ Мартин, Британская Колумбия; Бис, Д.А. (1992). «О генерации аэродинамического шума при вихреобразовании во вращающихся лопастях». Журнал звука и вибрации . 155 (2). Эльзевир Б.В.: 317–324. Бибкод : 1992JSV...155..317M . дои : 10.1016/0022-460x(92)90514-x . ISSN 0022-460X .
^ Моте, компакт-диск; Чжу, Вэнь Хуа (1 июля 1984 г.). «Аэродинамический шум в дальней зоне при работе дисковых пил на холостом ходу». Журнал вибрации и акустики . 106 (3). ASME International: 441–446. дои : 10.1115/1.3269215 . ISSN 1048-9002 .
^ Райтер, ВФ; Келти, РФ (1976). «О природе шума холостого хода дисковых пил». Журнал звука и вибрации . 44 (4). Эльзевир Б.В.: 531–543. Бибкод : 1976JSV....44..531R . дои : 10.1016/0022-460x(76)90095-x . ISSN 0022-460X .
^ Поблете, В., Аренас, Дж. П., Риос, Р., Миллар, Э. «Вибрация и шум холостого хода в коммерческих циркулярных пилах», Fifth Inter. Конгресс по звуку и вибрации, 1997 г.
^ Воннегут, Бернард (1954). «Вихревой свисток» . Журнал Акустического общества Америки . 26 (1). Акустическое общество Америки (ASA): 18–20. Бибкод : 1954ASAJ...26...18В . дои : 10.1121/1.1907282 . ISSN 0001-4966 .
^ Чано, Роберт К. (1963). «Опыты с вихревым свистком». Журнал Акустического общества Америки . 35 (7). Акустическое общество Америки (ASA): 953–960. Бибкод : 1963ASAJ...35..953C . дои : 10.1121/1.1918639 . ISSN 0001-4966 .
^ Чано, Роберт К. (1965). «Наблюдения колебательного движения в некоторых закрученных потоках». Журнал механики жидкости . 21 (1). Издательство Кембриджского университета (CUP): 111–127. Бибкод : 1965JFM....21..111C . дои : 10.1017/s0022112065000083 . ISSN 0022-1120 . S2CID 120369503 .
^ Пауэлл, Алан (1961). «На Эджтоне» . Журнал Акустического общества Америки . 33 (4). Акустическое общество Америки (ASA): 395–409. Бибкод : 1961ASAJ...33..395P . дои : 10.1121/1.1908677 . ISSN 0001-4966 .
^ Керл, Н. «Механика краевых тонов», Proc. Рой. Соц. А231, 505 (1955 г.).
^ Догерти, Б.Л., О'Фаррелл, Дж.М., Численное моделирование явления краевого тона", Отчет подрядчика НАСА 4581, 1994.
^ Росситер, Дж. Э. «Эксперименты в аэродинамической трубе по обтеканию прямоугольных полостей на дозвуковых и околозвуковых скоростях», Отчет 3438, Совет авиационных исследований (Великобритания), 1964.
^ Jump up to: ^а ^б Ли, Д.Дж., Ли, И.К., Хео, Д.Н., Ким, Ю.Н., «Численный анализ аэродинамического шума в результате явлений обратной связи с использованием вычислительной аэроакустики (CAA)», Proc. 12-й Азиатский конгресс по механике жидкости, август 2008 г.
^ Jump up to: ^а ^б Роули, Кларенс В.; Колониус, Тим; Басу, Амит Дж. (25 марта 2002 г.). «О автоколебаниях в двумерном сжимаемом потоке над прямоугольными полостями» (PDF) . Журнал механики жидкости . 455 (1). Издательство Кембриджского университета (CUP): 315–346. Бибкод : 2002JFM...455..315R . дои : 10.1017/s0022112001007534 . ISSN 0022-1120 . S2CID 17963868 .
^ «Мощные генераторы звуков и ультразвуков» .
^ Пауэлл, А. (1953). «О механизме шума удушающей струи». Труды Физического общества. Раздел Б. 66 (12). Издательство ИОП: 1039–1056. Бибкод : 1953PPSB...66.1039P . дои : 10.1088/0370-1301/66/12/306 . ISSN 0370-1301 .
^ Пауэлл, Алан (1 апреля 1954 г.). «Уменьшение шума удушающей струи». Труды Физического общества. Раздел Б. 67 (4). Издательство ИОП: 313–327. Бибкод : 1954PPSB...67..313P . дои : 10.1088/0370-1301/67/4/306 . ISSN 0370-1301 .
^ Лин, Дэн; Пауэлл, Алан (1997). «Симметричные режимы колебаний в тонах задушенной струи и визге из прямоугольных сопел». Журнал Акустического общества Америки . 102 (2). Акустическое общество Америки (ASA): 1235–1238. Бибкод : 1997ASAJ..102.1235L . дои : 10.1121/1.419614 . ISSN 0001-4966 .
^ Дэвис, М.Г., Олдфилд, Д.Э.С., «Тоны задушенной осесимметричной струи. I. Структура ячейки, скорость вихря и расположение источников», Acta Acustica, 12, 257–276 (1962).
^ Дэвис, М.Г., Олдфилд, Д.Э.С. «Тоны задушенной осесимметричной струи. II. Автовозбуждающаяся петля и режим колебаний», Acta Acustica, 12, 267–277 (1962).
^ Пауэлл, Алан; Умеда, Ёсикуни; Она, Рюдзи (1992). «Наблюдения за режимами колебаний задушенных круглых струй». Журнал Акустического общества Америки . 92 (5). Акустическое общество Америки (ASA): 2823–2836. Бибкод : 1992ЧЕТВЕРГ...92.2823P . дои : 10.1121/1.404398 . ISSN 0001-4966 .
^ Карпентер, В.; Пешинский, К. (2013). Данчова, Петра; Новонтый, Петр (ред.). «Странно ведущий себя жидкостный осциллятор» . Сеть конференций EPJ . 45 . EDP Science: 01074. Бибкод : 2013EPJWC..4501074T . дои : 10.1051/epjconf/20134501074 . ISSN 2100-014X .
^ Грегори, Джеймс В.; Салливан, Джон П.; Раман, Ганеша; Рагху, Сурья (2007). «Характеристика микрофлюидного генератора». Журнал АИАА . 45 (3). Американский институт аэронавтики и астронавтики (AIAA): 568–576. Бибкод : 2007AIAAJ..45..568G . дои : 10.2514/1.26127 . ISSN 0001-1452 .
^ Ким, Г., «Исследование жидкостных осцилляторов как альтернативного импульсного вихревого струйного привода для разделения потока», магистерская диссертация, Манчестерский университет, 2011.
^ Чано, Р.К. (1994). «Влияние геометрии на резонансную частоту резонаторов Гельмгольца». Журнал звука и вибрации . 178 (3). Эльзевир Б.В.: 337–348. Бибкод : 1994JSV...178..337C . дои : 10.1006/jsvi.1994.1490 . ISSN 0022-460X .
^ Чано, RC, Неопубликованная работа.
^ Нильсен, А.К., «Акустические резонаторы круглого сечения и с осевой симметрией», Труды Датской академии технических наук, 1949.
^ Дургин, В.В., Граф, Х.Р. «Возбуждаемый акустический резонанс в глубокой полости: аналитическая модель», Синпозиум по вибрации и шуму, вызванным потоком, 7, 1992.
^ Восток, LF (1966). «Аэродинамический резонанс в прямоугольных полостях». Журнал звука и вибрации . 3 (3). Эльзевир Б.В.: 277–287. Бибкод : 1966JSV.....3..277E . дои : 10.1016/0022-460x(66)90096-4 . ISSN 0022-460X .
^ Форестье, Николя; Жакен, Лоран; Жеффруа, Филипп (25 января 2003 г.). «Слой смешения над глубокой полостью при высокой дозвуковой скорости». Журнал механики жидкости . 475 (1). Издательство Кембриджского университета (CUP): 101–145. Бибкод : 2003JFM...475..101F . дои : 10.1017/s0022112002002537 . ISSN 0022-1120 . S2CID 122749863 .
^ Селамет, А.; Курниаван, Д.; Ноттс, Б.Д.; Новак, Дж. М. (2002). «Свистки с общей боковой ветвью: производство и подавление». Журнал звука и вибрации . 250 (2). Эльзевир Б.В.: 277–298. Бибкод : 2002JSV...250..277S . дои : 10.1006/jsvi.2001.3869 . ISSN 0022-460X .
^ Ноттс, Б.Д.; Селамет, А. (2003). «Подавление акустической связи потока в боковых каналах путем модификации интерфейса». Журнал звука и вибрации . 265 (5). Эльзевир Б.В.: 1025–1045. Бибкод : 2003JSV...265.1025K . дои : 10.1016/s0022-460x(02)01254-3 . ISSN 0022-460X .
^ Радавич, Пол М.; Селамет, Ахмет; Новак, Джеймс М. (2001). «Вычислительный подход к гидроакустической связи потока в закрытых боковых ветвях». Журнал Акустического общества Америки . 109 (4). Акустическое общество Америки (ASA): 1343–1353. Бибкод : 2001ASAJ..109.1343R . дои : 10.1121/1.1350618 . ISSN 0001-4966 . ПМИД 11325106 .
^ http://www.isb/ac./HS/JoP/index.html ^{[ мертвая ссылка ]}

[Wilson1971-1] Jump up to: ^а ^б Уилсон, штат Калифорния; Бобры, ГС; ДеКостер, Массачусетс; Хольгер, ДК; Регенфусс, доктор медицины (1971). «Опыты по гидромеханике свиста». Журнал Акустического общества Америки . 50 (1Б). Акустическое общество Америки (ASA): 366–372. Бибкод : 1971ASAJ...50..366W . дои : 10.1121/1.1912641 . ISSN 0001-4966 .

[scientificamerican.com-2] Чано, Роберт К. (январь 1970 г.). «Аэродинамические свистки» . Научный американец . 222 (1): 40–47. Бибкод : 1970SciAm.222a..40C . doi : 10.1038/scientificamerican0170-40 .

[3] Чано, Р.К., докторская диссертация, Калифорнийский университет, Лос-Анджелес, 1960.

[Chanaud1965-4] Jump up to: ^а ^б Чано, Колорадо; Пауэлл, Алан (1965). «Некоторые эксперименты относительно отверстия и рингтона» . Журнал Акустического общества Америки . 37 (5). Акустическое общество Америки (ASA): 902–911. Бибкод : 1965ASAJ...37..902C . дои : 10.1121/1.1909476 . ISSN 0001-4966 .

[5] Генривуд, Р.Х.; Агарвал, А. (2013). «Аэроакустика парового котла». Физика жидкостей . 25 (10). Издательство АИП: 107101–107101–23. Бибкод : 2013PhFl...25j7101H . дои : 10.1063/1.4821782 . ISSN 1070-6631 .

[6] Стратт, Дж. В. Барон Рэлей, Теория звука, MacMillan and Co., 1877.

[7] «Тентерфилдский лисий свисток — информационный бюллетень» .

[8] Накибоглу, Гюнеш; Руденко, Олексис; Хиршберг, Авраам (2012). «Аэроакустика качающейся гофрированной трубы: голос дракона» . Журнал Акустического общества Америки . 131 (1). Акустическое общество Америки (ASA): 749–765. Бибкод : 2012 ЧЕТВЕРГ..131..749N . дои : 10.1121/1.3651245 . ISSN 0001-4966 . ПМИД 22280698 .

[9] Раджавель, Б.; Прасад, МГ (1 июля 2014 г.). «Параметрические исследования акустики гофрированных труб с использованием моделирования больших вихрей (LES)». Инженерный журнал по контролю шума . 62 (4). Институт техники контроля шума (INCE): 218–231. дои : 10.3397/1/376222 . ISSN 0736-2501 .

[10] Лиза Р., Тейлор, МЭ, «Экспериментальное исследование акустических характеристик гофрированных трубок», Лаборатория контроля шума и вибрации, Технологический институт Стивенса, Диссертация, 1994.

[11] Картик, Б.; Чакраварти, СР; Суджит, Род-Айленд (2008). «Механизм возбуждения трубного тона потоком через отверстие в воздуховоде». Международный журнал аэроакустики . 7 (3–4). Публикации SAGE: 321–347. дои : 10.1260/1475-472x.7.3.321 . ISSN 1475-472X . S2CID 120954769 .

[12] Андерсон, ABC (1952). «Зависимость частоты пфейфентона (трубного тона) от длины трубы, диаметра отверстия и давления нагнетания газа». Журнал Акустического общества Америки . 24 (6). Акустическое общество Америки (ASA): 675–681. Бибкод : 1952ASAJ...24..675A . дои : 10.1121/1.1906955 . ISSN 0001-4966 .

[13] Андерсон, ABC (1953). «Число круглого отверстия, описывающее зависимость первичной частоты Пфейфентона от перепада давления, плотности газа и геометрии отверстия». Журнал Акустического общества Америки . 25 (4). Акустическое общество Америки (ASA): 626–631. Бибкод : 1953ASAJ...25..626A . дои : 10.1121/1.1907154 . ISSN 0001-4966 .

[14] Андерсон, ABC (1955). «Структура и скорость периодического вихрево-кольцевого режима течения первичной струи Пфейфентона (Трубного тона)». Журнал Акустического общества Америки . 27 (6). Акустическое общество Америки (ASA): 1048–1053. Бибкод : 1955ASAJ...27.1048A . дои : 10.1121/1.1908112 . ISSN 0001-4966 .

[15] Хартманн, июль (1 декабря 1922 г.). «О новом методе генерации звуковых волн» . Физический обзор . 20 (6). Американское физическое общество (APS): 719–727. Бибкод : 1922PhRv...20..719H . дои : 10.1103/physrev.20.719 . ISSN 0031-899X .

[16] Раман, Ганеша; Сринивасан, К. (2009). «Резонансная трубка с приводом: от открытия Хартмана до современных приложений активного управления потоком». Прогресс аэрокосмических наук . 45 (4–5). Эльзевир Б.В.: 97–123. Бибкод : 2009ПрАэС..45...97Р . doi : 10.1016/j.paerosci.2009.05.001 . ISSN 0376-0421 .

[17] Брун, Э.; Буше, RMG (1957). «Исследование акустического воздушно-реактивного генератора: новая разработка». Журнал Акустического общества Америки . 29 (5). Акустическое общество Америки (ASA): 573–583. Бибкод : 1957ASAJ...29..573B . дои : 10.1121/1.1908969 . ISSN 0001-4966 .

[18] Савой, Л.Е., «Эксперименты с акустическим генератором Хартмана», Engineering, 170, 99–100, 136–138 (1950).

[19] Матвеев К., «Термоакустические неустойчивости в трубке Рийке: эксперименты и моделирование». Диссертация, Калифорнийский институт. Тех., 2003.

[20] Бакхаус, С., Свифт, Г., «Новые разновидности термоакустических двигателей», 9-й Международный конгресс по звуку и вибрации, 2002.

[Birkenblattblasen-21] «Веет березовый лист в Гарце – Музыкальное дело Саксония-Анхальт» (на немецком языке) . Проверено 5 августа 2021 г.

[22] фон Карман, Т. «Аэродинамика», McGraw-Hill, 1963.

[23] Эткин, Б., Рибнер, Х. «Канадские исследования аэродинамического шума», Обзор 13, Институт физики, Univ. Торонто, 1958 год.

[24] Филлипс, О.М. (1956). «Интенсивность эоловых тонов». Журнал механики жидкости . 1 (6). Издательство Кембриджского университета (CUP): 607–624. Бибкод : 1956JFM.....1..607P . дои : 10.1017/s0022112056000408 . ISSN 0022-1120 . S2CID 120551027 .

[25] Хайден, Р.Э., Фокс, Х.Л., Чано, Р.К. «Некоторые факторы, влияющие на излучение от взаимодействия потока с краями конечных поверхностей», NASA CR-145073, 1976.

[26] Рщевкин С.Н., «Теория звука», The MacMillan Company, 1963.

[27] Бис, Д.А. (1992). «Аэродинамический шум циркулярной пилы». Журнал звука и вибрации . 154 (3). Эльзевир Б.В.: 495–513. Бибкод : 1992JSV...154..495B . дои : 10.1016/0022-460x(92)90782-s . ISSN 0022-460X .

[28] Мартин, Британская Колумбия; Бис, Д.А. (1992). «О генерации аэродинамического шума при вихреобразовании во вращающихся лопастях». Журнал звука и вибрации . 155 (2). Эльзевир Б.В.: 317–324. Бибкод : 1992JSV...155..317M . дои : 10.1016/0022-460x(92)90514-x . ISSN 0022-460X .

[29] Моте, компакт-диск; Чжу, Вэнь Хуа (1 июля 1984 г.). «Аэродинамический шум в дальней зоне при работе дисковых пил на холостом ходу». Журнал вибрации и акустики . 106 (3). ASME International: 441–446. дои : 10.1115/1.3269215 . ISSN 1048-9002 .

[30] Райтер, ВФ; Келти, РФ (1976). «О природе шума холостого хода дисковых пил». Журнал звука и вибрации . 44 (4). Эльзевир Б.В.: 531–543. Бибкод : 1976JSV....44..531R . дои : 10.1016/0022-460x(76)90095-x . ISSN 0022-460X .

[31] Поблете, В., Аренас, Дж. П., Риос, Р., Миллар, Э. «Вибрация и шум холостого хода в коммерческих циркулярных пилах», Fifth Inter. Конгресс по звуку и вибрации, 1997 г.

[32] Воннегут, Бернард (1954). «Вихревой свисток» . Журнал Акустического общества Америки . 26 (1). Акустическое общество Америки (ASA): 18–20. Бибкод : 1954ASAJ...26...18В . дои : 10.1121/1.1907282 . ISSN 0001-4966 .

[33] Чано, Роберт К. (1963). «Опыты с вихревым свистком». Журнал Акустического общества Америки . 35 (7). Акустическое общество Америки (ASA): 953–960. Бибкод : 1963ASAJ...35..953C . дои : 10.1121/1.1918639 . ISSN 0001-4966 .

[34] Чано, Роберт К. (1965). «Наблюдения колебательного движения в некоторых закрученных потоках». Журнал механики жидкости . 21 (1). Издательство Кембриджского университета (CUP): 111–127. Бибкод : 1965JFM....21..111C . дои : 10.1017/s0022112065000083 . ISSN 0022-1120 . S2CID 120369503 .

[Powell_1961_395–409-35] Пауэлл, Алан (1961). «На Эджтоне» . Журнал Акустического общества Америки . 33 (4). Акустическое общество Америки (ASA): 395–409. Бибкод : 1961ASAJ...33..395P . дои : 10.1121/1.1908677 . ISSN 0001-4966 .

[36] Керл, Н. «Механика краевых тонов», Proc. Рой. Соц. А231, 505 (1955 г.).

[37] Догерти, Б.Л., О'Фаррелл, Дж.М., Численное моделирование явления краевого тона", Отчет подрядчика НАСА 4581, 1994.

[38] Росситер, Дж. Э. «Эксперименты в аэродинамической трубе по обтеканию прямоугольных полостей на дозвуковых и околозвуковых скоростях», Отчет 3438, Совет авиационных исследований (Великобритания), 1964.

[ReferenceA-39] Jump up to: ^а ^б Ли, Д.Дж., Ли, И.К., Хео, Д.Н., Ким, Ю.Н., «Численный анализ аэродинамического шума в результате явлений обратной связи с использованием вычислительной аэроакустики (CAA)», Proc. 12-й Азиатский конгресс по механике жидкости, август 2008 г.

[Rowley2002-40] Jump up to: ^а ^б Роули, Кларенс В.; Колониус, Тим; Басу, Амит Дж. (25 марта 2002 г.). «О автоколебаниях в двумерном сжимаемом потоке над прямоугольными полостями» (PDF) . Журнал механики жидкости . 455 (1). Издательство Кембриджского университета (CUP): 315–346. Бибкод : 2002JFM...455..315R . дои : 10.1017/s0022112001007534 . ISSN 0022-1120 . S2CID 17963868 .

[41] «Мощные генераторы звуков и ультразвуков» .

[42] Пауэлл, А. (1953). «О механизме шума удушающей струи». Труды Физического общества. Раздел Б. 66 (12). Издательство ИОП: 1039–1056. Бибкод : 1953PPSB...66.1039P . дои : 10.1088/0370-1301/66/12/306 . ISSN 0370-1301 .

[43] Пауэлл, Алан (1 апреля 1954 г.). «Уменьшение шума удушающей струи». Труды Физического общества. Раздел Б. 67 (4). Издательство ИОП: 313–327. Бибкод : 1954PPSB...67..313P . дои : 10.1088/0370-1301/67/4/306 . ISSN 0370-1301 .

[44] Лин, Дэн; Пауэлл, Алан (1997). «Симметричные режимы колебаний в тонах задушенной струи и визге из прямоугольных сопел». Журнал Акустического общества Америки . 102 (2). Акустическое общество Америки (ASA): 1235–1238. Бибкод : 1997ASAJ..102.1235L . дои : 10.1121/1.419614 . ISSN 0001-4966 .

[45] Дэвис, М.Г., Олдфилд, Д.Э.С., «Тоны задушенной осесимметричной струи. I. Структура ячейки, скорость вихря и расположение источников», Acta Acustica, 12, 257–276 (1962).

[46] Дэвис, М.Г., Олдфилд, Д.Э.С. «Тоны задушенной осесимметричной струи. II. Автовозбуждающаяся петля и режим колебаний», Acta Acustica, 12, 267–277 (1962).

[47] Пауэлл, Алан; Умеда, Ёсикуни; Она, Рюдзи (1992). «Наблюдения за режимами колебаний задушенных круглых струй». Журнал Акустического общества Америки . 92 (5). Акустическое общество Америки (ASA): 2823–2836. Бибкод : 1992ЧЕТВЕРГ...92.2823P . дои : 10.1121/1.404398 . ISSN 0001-4966 .

[48] Карпентер, В.; Пешинский, К. (2013). Данчова, Петра; Новонтый, Петр (ред.). «Странно ведущий себя жидкостный осциллятор» . Сеть конференций EPJ . 45 . EDP Science: 01074. Бибкод : 2013EPJWC..4501074T . дои : 10.1051/epjconf/20134501074 . ISSN 2100-014X .

[49] Грегори, Джеймс В.; Салливан, Джон П.; Раман, Ганеша; Рагху, Сурья (2007). «Характеристика микрофлюидного генератора». Журнал АИАА . 45 (3). Американский институт аэронавтики и астронавтики (AIAA): 568–576. Бибкод : 2007AIAAJ..45..568G . дои : 10.2514/1.26127 . ISSN 0001-1452 .

[50] Ким, Г., «Исследование жидкостных осцилляторов как альтернативного импульсного вихревого струйного привода для разделения потока», магистерская диссертация, Манчестерский университет, 2011.

[51] Чано, Р.К. (1994). «Влияние геометрии на резонансную частоту резонаторов Гельмгольца». Журнал звука и вибрации . 178 (3). Эльзевир Б.В.: 337–348. Бибкод : 1994JSV...178..337C . дои : 10.1006/jsvi.1994.1490 . ISSN 0022-460X .

[52] Чано, RC, Неопубликованная работа.

[53] Нильсен, А.К., «Акустические резонаторы круглого сечения и с осевой симметрией», Труды Датской академии технических наук, 1949.

[54] Дургин, В.В., Граф, Х.Р. «Возбуждаемый акустический резонанс в глубокой полости: аналитическая модель», Синпозиум по вибрации и шуму, вызванным потоком, 7, 1992.

[55] Восток, LF (1966). «Аэродинамический резонанс в прямоугольных полостях». Журнал звука и вибрации . 3 (3). Эльзевир Б.В.: 277–287. Бибкод : 1966JSV.....3..277E . дои : 10.1016/0022-460x(66)90096-4 . ISSN 0022-460X .

[56] Форестье, Николя; Жакен, Лоран; Жеффруа, Филипп (25 января 2003 г.). «Слой смешения над глубокой полостью при высокой дозвуковой скорости». Журнал механики жидкости . 475 (1). Издательство Кембриджского университета (CUP): 101–145. Бибкод : 2003JFM...475..101F . дои : 10.1017/s0022112002002537 . ISSN 0022-1120 . S2CID 122749863 .

[57] Селамет, А.; Курниаван, Д.; Ноттс, Б.Д.; Новак, Дж. М. (2002). «Свистки с общей боковой ветвью: производство и подавление». Журнал звука и вибрации . 250 (2). Эльзевир Б.В.: 277–298. Бибкод : 2002JSV...250..277S . дои : 10.1006/jsvi.2001.3869 . ISSN 0022-460X .

[58] Ноттс, Б.Д.; Селамет, А. (2003). «Подавление акустической связи потока в боковых каналах путем модификации интерфейса». Журнал звука и вибрации . 265 (5). Эльзевир Б.В.: 1025–1045. Бибкод : 2003JSV...265.1025K . дои : 10.1016/s0022-460x(02)01254-3 . ISSN 0022-460X .

[59] Радавич, Пол М.; Селамет, Ахмет; Новак, Джеймс М. (2001). «Вычислительный подход к гидроакустической связи потока в закрытых боковых ветвях». Журнал Акустического общества Америки . 109 (4). Акустическое общество Америки (ASA): 1343–1353. Бибкод : 2001ASAJ..109.1343R . дои : 10.1121/1.1350618 . ISSN 0001-4966 . ПМИД 11325106 .

[60] ttp://www.isb/ac./HS/JoP/index.html ^{[ мертвая ссылка ]}

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]