Модель Морриса – Лекара

Модель Морриса-Лекара — это модель биологического нейрона, разработанная Кэтрин Моррис и Гарольдом Лекаром для воспроизведения разнообразия колебательного поведения по отношению к Ca. ⁺⁺ и К ⁺ проводимость в мышечных волокнах гигантского ракушка . ^{[ 1 ]} Нейроны Морриса-Лекара обладают возбудимостью нейронов как класса I, так и класса II .

История

Кэтрин Моррис (род. 24 декабря 1949 г.) - канадский биолог. Она выиграла стипендию Содружества для обучения в Кембриджском университете , где в 1977 году получила докторскую степень. она стала профессором Оттавского университета В начале 1980-х годов . По состоянию на 2015 год она является почетным профессором Оттавского университета. Гарольд Лекар (18 октября 1935 — 4 февраля 2014) — американский профессор биофизики и нейробиологии Калифорнийского университета в Беркли . В 1963 году он получил докторскую степень по физике в Колумбийском университете .

Экспериментальный метод

Эксперименты Морриса-Лекара основывались на методе фиксации напряжения, установленном Кейнсом и др. (1973). ^{[ 2 ]}

крупные экземпляры ракушки Balanus nubilus Использовали (Pacific Bio-Marine Laboratories Inc., Венеция, Калифорния). Ракушку распиливали на боковые половины и осторожно обнажали мышцы depressor scutorum rostralis. Отдельные волокна рассекали, разрез начинали от сухожилия. Другой конец мышцы разрезали вблизи места прикрепления к оболочке и лигатурировали. Изолированные волокна либо использовали сразу, либо перед использованием выдерживали до 30 мин в стандартной искусственной морской воде (ASW; см. ниже). Эксперименты проводились при комнатной температуре 22 °С . ^{[ 1 ]}

Основные предположения, лежащие в основе модели Морриса – Лекара.

Среди основных предположений можно назвать следующие:

Уравнения применимы к пространственно изопотенциальному участку мембраны. Существуют два постоянных (неинактивирующих) потенциалзависимых тока с противоположно смещенными реверсивными потенциалами. Деполяризующий ток переносится ионами Na+ или Ca2+ (или ими обоими), в зависимости от моделируемой системы, а гиперполяризующий ток переносится K+.
Активационные ворота достаточно быстро следуют за изменениями мембранного потенциала, поэтому активирующая проводимость может мгновенно релаксировать до своего установившегося значения при любом напряжении.
Динамику восстанавливающей переменной можно аппроксимировать линейным дифференциальным уравнением первого порядка для вероятности открытия канала. ^{[ 3 ]}

Физиологическое описание

Модель Морриса-Лекара представляет собой двумерную систему нелинейных дифференциальных уравнений . Она считается упрощенной моделью по сравнению с четырехмерной моделью Ходжкина – Хаксли .

Качественно эта система уравнений описывает сложную взаимосвязь между мембранным потенциалом и активацией ионных каналов внутри мембраны: потенциал зависит от активности ионных каналов, а активность ионных каналов — от напряжения. При изменении параметров бифуркации проявляются разные классы поведения нейронов. $τ N$ связан с относительными временными масштабами динамики обжига, которая широко варьируется от ячейки к ячейке и демонстрирует значительную температурную зависимость. ^{[ 3 ]}

Количественно:

{\begin{aligned}C{\frac {dV}{dt}}&~=~I-g_{\mathrm {L} }(V-V_{\mathrm {L} })-g_{\mathrm {Ca} }M_{\mathrm {ss} }(V-V_{\mathrm {Ca} })-g_{\mathrm {K} }N(V-V_{\mathrm {K} })\\[5pt]{\frac {dN}{dt}}&~=~{\frac {N_{\mathrm {ss} }-N}{\tau _{N}}}\end{aligned}}

где

{\begin{aligned}M_{\mathrm {ss} }&~=~{\frac {1}{2}}\cdot \left(1+\tanh \left[{\frac {V-V_{1}}{V_{2}}}\right]\right)\\[5pt]N_{\mathrm {ss} }&~=~{\frac {1}{2}}\cdot \left(1+\tanh \left[{\frac {V-V_{3}}{V_{4}}}\right]\right)\\[5pt]\tau _{N}&~=~1/\left(\varphi \cosh \left[{\frac {V-V_{3}}{2V_{4}}}\right]\right)\end{aligned}}

Обратите внимание, что $уравнения M ss$ и $N ss$ также могут быть выражены как $M ss = (1 + exp[-2(V - V 1) / V 2]) -1$ и $N ss = (1 + exp[-2(V - V 3) / V 4]) -1$ , однако большинство авторов предпочитают форму с использованием гиперболических функций.

Переменные

$V$ : membrane potential
$N$ : переменная восстановления: вероятность того, что канал K+ проводит

Параметры и константы

$Я$ : приложенный ток
$C$ : емкость мембраны
$г L$ , $г Ca$ , $г K$ : утечка, Ca ⁺⁺и К ⁺ проводимость через мембранный канал
$V L$ , $V Ca$ , $V K$ : равновесный потенциал соответствующих ионных каналов.
$V 1$ , $V 2$ , $V 3$ , $V 4$ : параметры настройки для установившегося режима и постоянной времени.
$φ$ : опорная частота

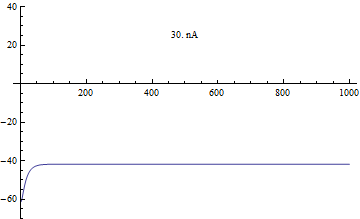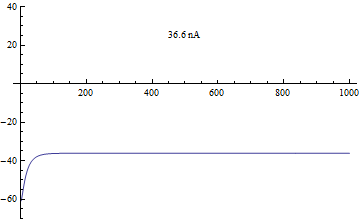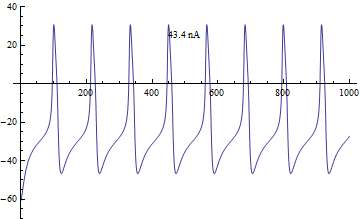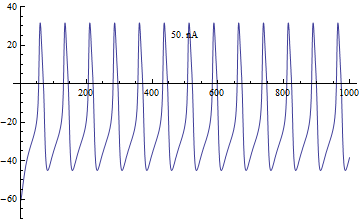
Бифуркации

Бифуркация в модели Морриса-Лекара анализировалась с приложенным током $I$ в качестве основного параметра бифуркации и $φ$ , $g Ca$ , $V 3$ , $V 4$ в качестве вторичных параметров для анализа фазовой плоскости . ^{[ 4 ]}

Возможные бифуркации

Бифуркация Хопфа

Бифуркация SNIC

Гомоклиническая бифуркация

Моделирование токового зажима модели Морриса – Лекара. Инжектируемый ток для бифуркации SNIC и гомоклинической бифуркации варьируется от 30 до 50 нА, тогда как ток для бифуркации Хопфа варьируется от 80 до 100 нА.

См. также

Ссылки

^ Перейти обратно: ^а ^б Моррис, Кэтрин; Лекар, Гарольд (июль 1981 г.), «Колебания напряжения в мышечных волокнах гигантских ракушек» , Biophys. J. , 35 (1): 193–213, Bibcode : 1981BpJ....35..193M , doi : 10.1016/S0006-3495(81)84782-0 , PMC 1327511 , PMID 7260316
^ Кейнс, РД ; Рохас, Э; Тейлор, Р.Э.; Вергара, Дж. (март 1973 г.), «Кальциевые и калиевые системы гигантского мышечного волокна ракушки под контролем мембранного потенциала» , The Journal of Physiology , 229 (2): 409–455, doi : 10.1113/jphysicalol.1973.sp010146 , PMC 1350315 , ПМИД 4724831 , заархивировано из оригинала 1 августа 2013 г.
^ Перейти обратно: ^а ^б Это предположение никогда не бывает полностью верным, поскольку белки каналов состоят из субъединиц, которые должны действовать согласованно, чтобы достичь открытого состояния. Несмотря на отсутствие задержек в начале восстановления, модель кажется адекватной для рассмотрения фазовой плоскости для многих возбудимых систем. Лекар, Гарольд (2007), «Модель Морриса-Лекара», Scholarpedia , 2 (10): 1333, Bibcode : 2007SchpJ...2.1333L , doi : 10.4249/scholarpedia.1333
^ Цумото, Куничика; Китаджимаб, Хироюки; Ёсинагак, Тецуя; Айхарад, Казуюки; Кавакамиф, Хироши (январь 2006 г.), «Бифуркации в модели нейронов Морриса-Лекара» (PDF) , Neurocomputing (на английском и японском языках), 69 (4–6): 293–316, doi : 10.1016/j.neucom.2005.03. 006 , заархивировано из оригинала (PDF) на 02 апреля 2012 г. , получено 10 сентября 2011 г.

Внешние ссылки

[ml81-1] Перейти обратно: ^а ^б Моррис, Кэтрин; Лекар, Гарольд (июль 1981 г.), «Колебания напряжения в мышечных волокнах гигантских ракушек» , Biophys. J. , 35 (1): 193–213, Bibcode : 1981BpJ....35..193M , doi : 10.1016/S0006-3495(81)84782-0 , PMC 1327511 , PMID 7260316

[2] Кейнс, РД ; Рохас, Э; Тейлор, Р.Э.; Вергара, Дж. (март 1973 г.), «Кальциевые и калиевые системы гигантского мышечного волокна ракушки под контролем мембранного потенциала» , The Journal of Physiology , 229 (2): 409–455, doi : 10.1113/jphysicalol.1973.sp010146 , PMC 1350315 , ПМИД 4724831 , заархивировано из оригинала 1 августа 2013 г.

[scholar-3] Перейти обратно: ^а ^б Это предположение никогда не бывает полностью верным, поскольку белки каналов состоят из субъединиц, которые должны действовать согласованно, чтобы достичь открытого состояния. Несмотря на отсутствие задержек в начале восстановления, модель кажется адекватной для рассмотрения фазовой плоскости для многих возбудимых систем. Лекар, Гарольд (2007), «Модель Морриса-Лекара», Scholarpedia , 2 (10): 1333, Bibcode : 2007SchpJ...2.1333L , doi : 10.4249/scholarpedia.1333

[4] Цумото, Куничика; Китаджимаб, Хироюки; Ёсинагак, Тецуя; Айхарад, Казуюки; Кавакамиф, Хироши (январь 2006 г.), «Бифуркации в модели нейронов Морриса-Лекара» (PDF) , Neurocomputing (на английском и японском языках), 69 (4–6): 293–316, doi : 10.1016/j.neucom.2005.03. 006 , заархивировано из оригинала (PDF) на 02 апреля 2012 г. , получено 10 сентября 2011 г.

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

v т и Нейронаука
Контур История
Базовый наука	Поведенческая эпигенетика Поведенческая генетика Картирование мозга Чтение мыслей Клеточная нейробиология Вычислительная нейробиология Коннектомика Визуализация генетики Интегративная нейробиология Молекулярная нейробиология Нейронное декодирование Нейронная инженерия Нейроанатомия Нейробиология Нейрохимия Нейроэндокринология Нейрогенетика Нейроинформатика Нейрометрика Нейроморфология Нейрофизика Нейрофизиология Системная нейробиология
Клинический нейробиология	Поведенческая неврология Клиническая нейрофизиология Эпилептология Нейрокардиология Нейроэпидемиология Нейрогастроэнтерология Нейроиммунология Нейроинтенсивная терапия Неврология Нейроонкология Нейроофтальмология Невропатология Нейрофармакология Нейропротезирование Нейропсихиатрия Нейрорадиология Нейрореабилитация Нейрохирургия Нейротология Нейровирусология Пищевая нейробиология Психиатрия
Когнитивный нейробиология	Аффективная нейробиология Поведенческая нейробиология Хронобиология Молекулярно-клеточное познание Управление двигателем Нейролингвистика Нейропсихология Сенсорная нейробиология Социальная когнитивная нейробиология
Междисциплинарный поля	Потребительская нейробиология Культурная нейробиология Образовательная нейробиология Эволюционная нейробиология Глобальная нейрохирургия Нейроантропология Нейронная инженерия Нейробиотики Нейрокриминология Нейроэкономика Нейроэпистемология Нейроэстетика Нейроэтика Нейроэтология Нейроистория Нейрозакон Нейромаркетинг Нейроморфная инженерия Нейрофеноменология Нейрофилософия Нейрополитика Нейробототехника Нейротеология Палеонейробиология Социальная нейробиология
Концепции	Интерфейс мозг-компьютер Развитие нервной системы Нейронная сеть (искусственная) Нейронная сеть (биологическая) Теория обнаружения Интраоперационный нейрофизиологический мониторинг Нейрочип Нейродегенеративное заболевание Нарушение нервно-психического развития Нейроразнообразие Нейрогенез Нейровизуализация Нейроиммунная система Нейроменеджмент Нейромодуляция Нейропластичность Нейротехнологии нейротоксин
Категория Коммонс