Гомоморфизм

В алгебре гомоморфизм группами — это сохраняющее структуру отображение между двумя алгебраическими структурами одного и того же типа (например, двумя , двумя кольцами или двумя векторными пространствами ). Слово гомоморфизм происходит от древнегреческого языка : ὁμός ( homos ) означает «тот же» и μορφή ( morphe ) означает «форма» или «форма». Однако это слово, по-видимому, было введено в математику из-за (неправильного) перевода немецкого слова ähnlich , означающего «похожий», на ὁμός, означающего «тот же самый». ^[1] Термин «гомоморфизм» появился еще в 1892 году, когда его приписали немецкому математику Феликсу Клейну (1849–1925). ^[2]

Гомоморфизмы векторных пространств называются также линейными отображениями , и их изучение составляет предмет линейной алгебры .

Понятие гомоморфизма было обобщено под названием морфизма на многие другие структуры, которые либо не имеют основного множества, либо не являются алгебраическими. Это обобщение является отправной точкой теории категорий .

Гомоморфизм может быть также изоморфизмом , эндоморфизмом , автоморфизмом и т. д. (см. ниже). Каждый из них можно определить таким образом, чтобы его можно было обобщить на любой класс морфизмов.

Определение

Гомоморфизм — это отображение между двумя алгебраическими структурами одного и того же типа (например, двумя группами, двумя полями, двумя векторными пространствами), которое сохраняет операции структур. Это означает карту $f:A\to B$ между двумя наборами $A$ , $B$ оснащен такой же конструкцией, что, если $\cdot$ — операция структуры (здесь для упрощения предполагается, что это бинарная операция ), то

f(x\cdot y)=f(x)\cdot f(y)

за каждую пару $x$ , $y$ элементов $A$ . ^{[примечание 1]} Часто говорят, что $f$ сохраняет операцию или совместим с ней.

Формально карта $f:A\to B$ сохраняет операцию $\mu$ арности $k$ , определенный на обоих $A$ и $B$ если

f(\mu _{A}(a_{1},\ldots ,a_{k}))=\mu _{B}(f(a_{1}),\ldots ,f(a_{k})),

для всех элементов $a_{1},...,a_{k}$ в $A$ .

Операции, которые должны сохраняться гомоморфизмом, включают 0-арные операции , то есть константы. В частности, когда элемент идентификации требуется для типа структуры, элемент идентификации первой структуры должен быть отображен на соответствующий элемент идентификации второй структуры.

Например:

— Гомоморфизм полугрупп это отображение между полугруппами , сохраняющее операцию полугруппы.
— Гомоморфизм моноида это отображение между моноидами , которое сохраняет операцию моноида и отображает единичный элемент первого моноида в элемент второго моноида (единичный элемент — это 0-арная операция ).
Групповой гомоморфизм — это отображение между группами , сохраняющее групповую операцию. Это означает, что групповой гомоморфизм отображает единичный элемент первой группы в единичный элемент второй группы и отображает обратный элемент первой группы в обратный образ этого элемента. Таким образом, полугрупповой гомоморфизм между группами обязательно является групповым гомоморфизмом.
Гомоморфизм колец — это отображение между кольцами , которое сохраняет сложение колец, умножение колец и мультипликативное тождество . Сохранится ли мультипликативная идентичность, зависит от определения кольца используемого . Если мультипликативное тождество не сохраняется, то имеется гомоморфизм rng .
Линейное отображение — это гомоморфизм векторных пространств ; то есть групповой гомоморфизм между векторными пространствами, который сохраняет структуру абелевой группы и скалярное умножение .
Гомоморфизм модулей , также называемый линейным отображением между модулями , определяется аналогично.
— Гомоморфизм алгебры это отображение, сохраняющее алгебраические операции.

Алгебраическая структура может иметь более одной операции, и для сохранения каждой операции требуется гомоморфизм. Таким образом, отображение, сохраняющее лишь некоторые операции, не является гомоморфизмом структуры, а лишь гомоморфизмом подструктуры, полученной при рассмотрении только сохранившихся операций. Например, отображение между моноидами, сохраняющее операцию моноида, а не единичный элемент, не является гомоморфизмом моноида, а только гомоморфизмом полугруппы.

Обозначения операций не обязательно должны быть одинаковыми в источнике и цели гомоморфизма. Например, действительные числа образуют группу для сложения, а положительные действительные числа образуют группу для умножения. Показательная функция

x\mapsto e^{x}

удовлетворяет

e^{x+y}=e^{x}e^{y},

и, таким образом, является гомоморфизмом между этими двумя группами. Это даже изоморфизм (см. ниже), поскольку его обратная функция , натуральный логарифм , удовлетворяет условию

\ln(xy)=\ln(x)+\ln(y),

и также является гомоморфизмом группы.

Примеры

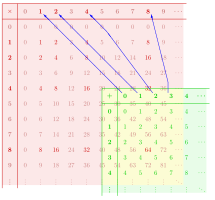
Действительные числа представляют собой кольцо , в котором есть как сложение, так и умножение. Множество всех матриц 2×2 также является кольцом при сложении и умножении матриц . Если мы определим функцию между этими кольцами следующим образом:

f(r)={\begin{pmatrix}r&0\\0&r\end{pmatrix}}

где $r$ — действительное число, то $f$ — гомоморфизм колец, поскольку $f$ сохраняет оба сложения:

f(r+s)={\begin{pmatrix}r+s&0\\0&r+s\end{pmatrix}}={\begin{pmatrix}r&0\\0&r\end{pmatrix}}+{\begin{pmatrix}s&0\\0&s\end{pmatrix}}=f(r)+f(s)

и умножение:

f(rs)={\begin{pmatrix}rs&0\\0&rs\end{pmatrix}}={\begin{pmatrix}r&0\\0&r\end{pmatrix}}{\begin{pmatrix}s&0\\0&s\end{pmatrix}}=f(r)\,f(s).

Другой пример: ненулевые комплексные числа образуют группу при операции умножения, как и ненулевые действительные числа. (Ноль необходимо исключить из обеих групп, поскольку он не имеет мультипликативного обратного значения , которое требуется для элементов группы.) Определите функцию $f$ от ненулевых комплексных чисел к ненулевым действительным числам с помощью

f(z)=|z|.

То есть, $f$ - абсолютное значение (или модуль) комплексного числа $z$ . Затем $f$ является гомоморфизмом групп, так как сохраняет умножение:

f(z_{1}z_{2})=|z_{1}z_{2}|=|z_{1}||z_{2}|=f(z_{1})f(z_{2}).

Обратите внимание, что $f$ нельзя расширить до гомоморфизма колец (от комплексных чисел до действительных чисел), поскольку он не сохраняет сложение:

|z_{1}+z_{2}|\neq |z_{1}|+|z_{2}|.

В качестве другого примера на диаграмме показан моноида . гомоморфизм $f$ из моноида $(\mathbb {N} ,+,0)$ к моноиду $(\mathbb {N} ,\times ,1)$ . Из-за разных названий соответствующих операций свойства сохранения структуры, удовлетворяемые $f$ составлять $f(x+y)=f(x)\times f(y)$ и $f(0)=1$ .

Композиционная алгебра $A$ над полем $F$ имеет квадратичную форму , называемую нормой , $N:A\to F$ , который является групповым гомоморфизмом мультипликативной группы $A$ в мультипликативную группу $F$ .

Специальные гомоморфизмы

Некоторые виды гомоморфизмов имеют особое название, которое также определено для общих морфизмов .

изоморфизм

Изоморфизм одного и между алгебраическими структурами того же типа обычно определяется как биективный гомоморфизм. ^[3]^: 134 ^[4]^: 28

В более общем контексте теории категорий изоморфизм определяется как морфизм , который имеет обратный, который также является морфизмом. В конкретном случае алгебраических структур эти два определения эквивалентны, хотя они могут различаться для неалгебраических структур, имеющих базовый набор.

Точнее, если

f:A\to B

является (гомо)морфизмом, он имеет обратный, если существует гомоморфизм

g:B\to A

такой, что

f\circ g=\operatorname {Id} _{B}\qquad {\text{and}}\qquad g\circ f=\operatorname {Id} _{A}.

Если $A$ и $B$ иметь базовые наборы и $f:A\to B$ имеет обратную $g$ , затем $f$ является биективным. Фактически, $f$ является инъективным , так как $f(x)=f(y)$ подразумевает $x=g(f(x))=g(f(y))=y$ , и $f$ сюръективен , как и любой $x$ в $B$ , у одного есть $x=f(g(x))$ , и $x$ это изображение элемента $A$ .

И наоборот, если $f:A\to B$ является биективным гомоморфизмом между алгебраическими структурами, пусть $g:B\to A$ быть картой такой, что $g(y)$ это уникальный элемент $x$ из $A$ такой, что $f(x)=y$ . У одного есть $f\circ g=\operatorname {Id} _{B}{\text{ and }}g\circ f=\operatorname {Id} _{A},$ и осталось только показать, что $g$ — гомоморфизм. Если $*$ — бинарная операция структуры, для каждой пары $x$ , $y$ элементов $B$ , у одного есть

g(x*_{B}y)=g(f(g(x))*_{B}f(g(y)))=g(f(g(x)*_{A}g(y)))=g(x)*_{A}g(y),

и $g$ таким образом, совместим с $*.$ Поскольку доказательство аналогично для любой арности , это показывает, что $g$ является гомоморфизмом.

Это доказательство не работает для неалгебраических структур. Например, для топологических пространств морфизм является непрерывным отображением , а обратное биективному непрерывному отображению не обязательно является непрерывным. Таким образом, изоморфизм топологических пространств, называемый гомеоморфизмом или бинепрерывным отображением , является биективным непрерывным отображением, обратное к которому также непрерывно.

эндоморфизм

Эндоморфизм равна — это гомоморфизм, область определения которого кодомену , или , в более общем смысле, морфизм , источник которого равен его цели. ^[3]^: 135

Эндоморфизмы алгебраической структуры или объекта категории образуют моноид при композиции.

Эндоморфизмы векторного пространства или модуля образуют кольцо . В случае векторного пространства или свободного модуля конечной размерности выбор базиса индуцирует кольцевой изоморфизм между кольцом эндоморфизмов и кольцом квадратных матриц той же размерности.

Автоморфизм

Автоморфизм — это эндоморфизм, который также является изоморфизмом. ^[3]^: 135

Автоморфизмы алгебраической структуры или объекта категории образуют группу по композиции, которая называется группой автоморфизмов структуры.

Многие группы, получившие название, представляют собой группы автоморфизмов некоторой алгебраической структуры. Например, общая линейная группа $\operatorname {GL} _{n}(k)$ — группа автоморфизмов векторного пространства размерности $n$ над полем $k$ .

Группы автоморфизмов были введены Эваристом Галуа для изучения корней многочленов полей и являются основой теории Галуа .

Мономорфизм

Для алгебраических структур мономорфизмы обычно определяются как инъективные гомоморфизмы. ^[3]^: 134 ^[4]^: 29

В более общем контексте теории категорий мономорфизм определяется как морфизм, который можно сократить слева . ^[5] Это означает, что (гомо)морфизм $f:A\to B$ является мономорфизмом, если для любой пары $g$ , $h$ морфизмов любого другого объекта $C$ к $A$ , затем $f\circ g=f\circ h$ подразумевает $g=h$ .

Эти два определения мономорфизма эквивалентны для всех обычных алгебраических структур. Точнее, они эквивалентны для полей , для которых всякий гомоморфизм является мономорфизмом, и для многообразий универсальной алгебры , то есть алгебраических структур, для которых операции и аксиомы (тождества) определены без каких-либо ограничений (поля не образуют многообразия, поскольку мультипликативная обратная операция определяется либо как унарная операция , либо как свойство умножения, которые в обоих случаях определяются только для ненулевых элементов).

В частности, два определения мономорфизма эквивалентны для множеств , магм , полугрупп , моноидов , групп , колец , полей , векторных пространств и модулей .

Расщепляемый мономорфизм — это гомоморфизм, который имеет левый обратный и, следовательно, сам является правым обратным этому другому гомоморфизму. То есть гомоморфизм $f\colon A\to B$ является расщепляемым мономорфизмом, если существует гомоморфизм $g\colon B\to A$ такой, что $g\circ f=\operatorname {Id} _{A}.$ Расщепляемый мономорфизм всегда является мономорфизмом для обоих значений мономорфизма . Для множеств и векторных пространств каждый мономорфизм является расщепляемым мономорфизмом, но это свойство не выполняется для большинства распространенных алгебраических структур.

Доказательство эквивалентности двух определений мономорфизмов.

An injective homomorphism is left cancelable: If $f\circ g=f\circ h,$ one has $f(g(x))=f(h(x))$ for every $x$ in $C$ , the common source of $g$ and $h$ . If $f$ is injective, then $g(x)=h(x)$ , and thus $g=h$ . This proof works not only for algebraic structures, but also for any category whose objects are sets and arrows are maps between these sets. For example, an injective continuous map is a monomorphism in the category of topological spaces.

For proving that, conversely, a left cancelable homomorphism is injective, it is useful to consider a free object on $x$ . Given a variety of algebraic structures a free object on $x$ is a pair consisting of an algebraic structure $L$ of this variety and an element $x$ of $L$ satisfying the following universal property: for every structure $S$ of the variety, and every element $s$ of $S$ , there is a unique homomorphism $f:L\to S$ such that $f(x)=s$ . For example, for sets, the free object on $x$ is simply $\{x\}$ ; for semigroups, the free object on $x$ is $\{x,x^{2},\ldots ,x^{n},\ldots \},$ which, as, a semigroup, is isomorphic to the additive semigroup of the positive integers; for monoids, the free object on $x$ is $\{1,x,x^{2},\ldots ,x^{n},\ldots \},$ which, as, a monoid, is isomorphic to the additive monoid of the nonnegative integers; for groups, the free object on $x$ is the infinite cyclic group $\{\ldots ,x^{-n},\ldots ,x^{-1},1,x,x^{2},\ldots ,x^{n},\ldots \},$ which, as, a group, is isomorphic to the additive group of the integers; for rings, the free object on $x$ is the polynomial ring $\mathbb {Z} [x];$ for vector spaces or modules, the free object on $x$ is the vector space or free module that has $x$ as a basis.

If a free object over $x$ exists, then every left cancelable homomorphism is injective: let $f\colon A\to B$ be a left cancelable homomorphism, and $a$ and $b$ be two elements of $A$ such $f(a)=f(b)$ . By definition of the free object $F$ , there exist homomorphisms $g$ and $h$ from $F$ to $A$ such that $g(x)=a$ and $h(x)=b$ . As $f(g(x))=f(h(x))$ , one has $f\circ g=f\circ h,$ by the uniqueness in the definition of a universal property. As $f$ is left cancelable, one has $g=h$ , and thus $a=b$ . Therefore, $f$ is injective.

Existence of a free object on $x$ for a variety (see also Free object § Existence): For building a free object over $x$ , consider the set $W$ of the well-formed formulas built up from $x$ and the operations of the structure. Two such formulas are said equivalent if one may pass from one to the other by applying the axioms (identities of the structure). This defines an equivalence relation, if the identities are not subject to conditions, that is if one works with a variety. Then the operations of the variety are well defined on the set of equivalence classes of $W$ for this relation. It is straightforward to show that the resulting object is a free object on $x$ .

Эпиморфизм

В алгебре эпиморфизмы сюръективные часто определяются как гомоморфизмы . ^[3]^: 134^[4]^: 43 С другой стороны, в теории категорий эпиморфизмы определяются как сокращаемые справа морфизмы . ^[5] Это означает, что (гомо)морфизм $f:A\to B$ является эпиморфизмом, если для любой пары $g$ , $h$ морфизмов из $B$ к любому другому объекту $C$ , равенство $g\circ f=h\circ f$ подразумевает $g=h$ .

Сюръективный гомоморфизм всегда сокращаем справа, но обратное не всегда верно для алгебраических структур. Однако два определения эпиморфизма эквивалентны для множеств , векторных пространств , абелевых групп , модулей (доказательство см. ниже) и групп . ^[6] Важность этих структур во всей математике, особенно в линейной алгебре и гомологической алгебре , может объяснить сосуществование двух неэквивалентных определений.

Алгебраические структуры, для которых существуют несюръективные эпиморфизмы, включают полугруппы и кольца . Самый простой пример — включение целых чисел в рациональные числа , что является гомоморфизмом колец и мультипликативных полугрупп. Для обеих структур это мономорфизм и несюръективный эпиморфизм, но не изоморфизм. ^[5]^[7]

Широким обобщением этого примера является локализация кольца мультипликативным множеством. Каждая локализация представляет собой кольцевой эпиморфизм, который, вообще говоря, не является сюръективным. Поскольку локализации являются фундаментальными в коммутативной алгебре и алгебраической геометрии , это может объяснить, почему в этих областях обычно предпочтительнее определение эпиморфизмов как сокращаемых справа гомоморфизмов.

Расщепляемый эпиморфизм — это гомоморфизм, который имеет правый обратный и, следовательно, сам является левым обратным этому другому гомоморфизму. То есть гомоморфизм $f\colon A\to B$ является расщепляемым эпиморфизмом, если существует гомоморфизм $g\colon B\to A$ такой, что $f\circ g=\operatorname {Id} _{B}.$ Расщепляемый эпиморфизм всегда является эпиморфизмом для обоих значений эпиморфизма . Для множеств и векторных пространств каждый эпиморфизм является расщепляемым эпиморфизмом, но это свойство не выполняется для большинства распространенных алгебраических структур.

Таким образом, у человека есть

{\text{split epimorphism}}\implies {\text{epimorphism (surjective)}}\implies {\text{epimorphism (right cancelable)}};

последнее импликация — это эквивалентность множеств, векторных пространств, модулей, абелевых групп и групп; первое следствие — это эквивалентность множеств и векторных пространств.

Эквивалентность двух определений эпиморфизма

Let $f\colon A\to B$ be a homomorphism. We want to prove that if it is not surjective, it is not right cancelable.

In the case of sets, let $b$ be an element of $B$ that not belongs to $f(A)$ , and define $g,h\colon B\to B$ such that $g$ is the identity function, and that $h(x)=x$ for every $x\in B,$ except that $h(b)$ is any other element of $B$ . Clearly $f$ is not right cancelable, as $g\neq h$ and $g\circ f=h\circ f.$

In the case of vector spaces, abelian groups and modules, the proof relies on the existence of cokernels and on the fact that the zero maps are homomorphisms: let $C$ be the cokernel of $f$ , and $g\colon B\to C$ be the canonical map, such that $g(f(A))=0$ . Let $h\colon B\to C$ be the zero map. If $f$ is not surjective, $C\neq 0$ , and thus $g\neq h$ (one is a zero map, while the other is not). Thus $f$ is not cancelable, as $g\circ f=h\circ f$ (both are the zero map from $A$ to $C$ ).

Ядро

Любой гомоморфизм $f:X\to Y$ определяет отношение эквивалентности $\sim$ на $X$ к $a\sim b$ тогда и только тогда, когда $f(a)=f(b)$ . Отношение $\sim$ называется ядром $f$ . Это отношение конгруэнтности на $X$ . Набор факторов $X/{\sim }$ тогда можно задать структуру того же типа, что и $X$ естественным образом, определяя операции фактормножества по $[x]\ast [y]=[x\ast y]$ , для каждой операции $\ast$ из $X$ . В этом случае изображение $X$ в $Y$ при гомоморфизме $f$ обязательно изоморфен $X/\!\sim$ ; этот факт является одной из теорем изоморфизма .

Когда алгебраическая структура представляет собой группу для некоторой операции, класс эквивалентности $K$ единичного элемента этой операции достаточно, чтобы охарактеризовать отношение эквивалентности. В этом случае фактор по отношению эквивалентности обозначается через $X/K$ (обычно читается как « $X$ против $K$ "). Также в данном случае это $K$ , скорее, чем $\sim$ называется ядром , которое $f$ . Ядра гомоморфизмов данного типа алгебраической структуры естественным образом наделены некоторой структурой. Этот тип структуры ядер такой же, как и рассматриваемая структура, в случае абелевых групп , векторных пространств и модулей , но отличается и получил конкретное название в других случаях, например нормальная подгруппа для ядер групповых гомоморфизмов и идеалов. для ядер кольцевых гомоморфизмов (в случае некоммутативных колец ядрами являются двусторонние идеалы ).

Реляционные структуры

В теории моделей понятие алгебраической структуры обобщается на структуры, включающие как операции, так и отношения. Пусть L — сигнатура, состоящая из символов функции и отношения, а A , B — две L -структуры. Тогда гомоморфизм из A в B — это отображение h из области определения A в область определения B такое, что

ч ( Ф ^А( а ₁ ,…, а _п )) = F ^Б( h ( a ₁ ),…, h ( an ₎ ) для каждого n -арного функционального символа F в L ,
Р ^А( a ₁ …, an _, ) влечет R ^Б( h ( a ₁ ),…, h ( an ₎ ) для каждого n -арного символа отношения R в L .

В частном случае всего с одним бинарным отношением мы получаем понятие гомоморфизма графа . ^[8]

Формальная теория языка

Гомоморфизмы также используются при изучении формальных языков. ^[9] и их часто кратко называют морфизмами . ^[10] Данные алфавиты $\Sigma _{1}$ и $\Sigma _{2}$ , функция $h\colon \Sigma _{1}^{*}\to \Sigma _{2}^{*}$ такой, что $h(uv)=h(u)h(v)$ для всех $u,v\in \Sigma _{1}$ называется гомоморфизмом на $\Sigma _{1}^{*}$ . ^{[примечание 2]} Если $h$ является гомоморфизмом на $\Sigma _{1}^{*}$ и $\varepsilon$ обозначает пустую строку, тогда $h$ называется $\varepsilon$ -свободный гомоморфизм, когда $h(x)\neq \varepsilon$ для всех $x\neq \varepsilon$ в $\Sigma _{1}^{*}$ .

Гомоморфизм $h\colon \Sigma _{1}^{*}\to \Sigma _{2}^{*}$ на $\Sigma _{1}^{*}$ это удовлетворяет $|h(a)|=k$ для всех $a\in \Sigma _{1}$ называется $k$ -равномерный гомоморфизм. ^[11] Если $|h(a)|=1$ для всех $a\in \Sigma _{1}$ (то есть, $h$ является 1-равномерным), то $h$ также называется кодированием или проекцией . ^{[ нужна ссылка ]}

Набор $\Sigma ^{*}$ слов, составленных из алфавита $\Sigma$ можно рассматривать как свободный моноид, порожденный $\Sigma$ . Здесь операция моноида — это конкатенация , а единичный элемент — пустое слово. С этой точки зрения языковой гомоморфизм — это в точности моноидный гомоморфизм. ^{[примечание 3]}

См. также

Диффеоморфизм
Гомоморфное шифрование
Гомоморфное разделение секретов – упрощенный протокол децентрализованного голосования
Морфизм
Квазиморфизм

Примечания

^ Как это часто бывает, но не всегда, один и тот же символ для обозначения работы обоих $A$ и $B$ здесь использовался.
^ Символ ∗ обозначает операцию звезды Клини , а Σ ^∗ обозначает набор слов, образованных из алфавита Σ, включая пустое слово. Сопоставление терминов означает конкатенацию . Например, h ( u ) h ( v ) обозначает объединение h ( u ) с h ( v ).
^ Нас уверяют, что языковой гомоморфизм h отображает пустое слово ε в пустое слово. Поскольку час ( ε ) = час ( ε ) = час ( ε ) час ( ε ), количество w символов в h ( ε ) равно числу 2 w символов в h ( ε ) h ( ε ). Следовательно, w = 0 и h ( ε ) имеет нулевую длину.

Цитаты

^ Фрике, Роберт (1897–1912). Лекции по теории автоморфных функций . Б. Г. Тойбнер. ОСЛК 29857037 .
^
См.:
- Риттер, Эрнст (1892). «Уникальные автоморфные формы нулевого пола, пересмотр и расширение теоремы Пуанкаре » . Математические анналы (на немецком языке). 41 :1-82. дои : 10.1007/BF01443449 . S2CID 121524108 . Из сноски на стр. 22 : «Я хочу следовать предложению проф. Клейна вместо громоздких и не всегда достаточных терминов: «голоэдрический, или. гемиэдрические и т. д. изоморфные» ограничивают обозначение «изоморфные» случаем голоэдрического изоморфизма двух групп, а в противном случае говорят о «гомоморфизме»,...» (Следуя предложению проф. Клейна, вместо громоздкого и не громоздкого всегда удовлетворительные обозначения «голоэдрический, или полуэдрический и т. д. изоморфный», я ограничу наименование «изоморфный» случаем голоэдрического изоморфизма двух групп, однако в противном случае [я буду] говорить о «гомоморфизме»,…)
- Фрике, Роберт (1892). «Об арифметическом характере функций треугольника, принадлежащих точкам ветвления (2,3,7) и (2,4,7)». Математические анналы (на немецком языке). 41 (3): 443–468. дои : 10.1007/BF01443421 . S2CID 120022176 . Из стр. 466: «Как видно непосредственно, это устанавливает гомоморфное*) отношение группы Г ₍₆₃₎ к группе мод. п неконгруэнтных замен с целыми рациональными коэффициентами определителя 1». (Таким образом, как сразу видно, гомоморфное отношение группы Г ₍₆₃₎ основано на группе неконгруэнтных по модулю n подстановок с целыми рациональными коэффициентами определителя 1.) Из сноски на с. 466: «*) Следуя обычаю, введенному г-ном Клейном в его последних лекциях, я пишу более подходящий «гомоморфизм» вместо прежнего термина «мероэдральный изоморфизм».» (Следуя использованию, введенному г-ном Кляйном в его последних лекциях, я пишу вместо прежнего обозначения «мероэдральный изоморфизм» более логичное «гомоморфизм».)
^ Jump up to: ^а ^б ^с ^д ^и Биркгоф, Гарретт (1967) [1940], Теория решетки , Публикации коллоквиума Американского математического общества, том. 25 (3-е изд.), Провиденс, Род-Айленд: Американское математическое общество , ISBN. 978-0-8218-1025-5 , МР 0598630
^ Jump up to: ^а ^б ^с Стэнли Н. Беррис; HP Санкаппанавар (2012). Курс универсальной алгебры (PDF) . С. Беррис и Х. П. Санкаппанавар. ISBN 978-0-9880552-0-9 .
^ Jump up to: ^а ^б ^с Мак Лейн, Сондерс (1971). Категории для работающего математика . Тексты для аспирантов по математике . Том. 5. Шпрингер-Верлаг . Упражнение 4 в разделе I.5. ISBN 0-387-90036-5 . Збл 0232.18001 .
^ Линдерхольм, CE (1970). Групповой эпиморфизм сюръективен. Американский математический ежемесячник , 77 (2), 176–177.
^ Даскалеску, Сорин; Нэстасеску, Константин; Райану, Шербан (2001). Алгебра Хопфа: Введение . Чистая и прикладная математика. Том 235. Нью-Йорк, Нью-Йорк: Марсель Деккер. стр. 363. ISBN 0824704819 . Збл 0962.16026 .
^ Подробное обсуждение реляционных гомоморфизмов и изоморфизмов см. в разделе 17.3, в Gunther Schmidt , 2010. Relational Mathematics . Издательство Кембриджского университета, ISBN 978-0-521-76268-7
^ Сеймур Гинзбург , Алгебраические и теоретико-автоматные свойства формальных языков , Северная Голландия, 1975, ISBN 0-7204-2506-9 ,
^ Т. Харью, Дж. Кархумеки, Морфизмы в Справочнике по формальным языкам , Том I, под редакцией Г. Розенберга, А. Саломаа, Springer, 1997, ISBN 3-540-61486-9 .
^ Воин (2006) с. 287

Ссылки

Кригер, Далия (2006). «О критических показателях в неподвижных точках нестирающихся морфизмов». В Ибарре, Оскар Х.; Данг, Чжэ (ред.). Развитие теории языка: 10-я международная конференция, DLT 2006, Санта-Барбара, Калифорния, США, 26–29 июня 2006 г.: материалы . Берлин: Шпрингер. стр. 280–291. ISBN 978-3-540-35430-7 . OCLC 262693179 .
Стэнли Н. Беррис; HP Санкаппанавар (2012). Курс универсальной алгебры (PDF) . С. Беррис и Х. П. Санкаппанавар. ISBN 978-0-9880552-0-9 .
Мак Лейн, Сондерс (1971), Категории для работающего математика , Тексты для выпускников по математике , том. 5, Шпрингер-Верлаг , ISBN 0-387-90036-5 , Збл 0232.18001
Фрели, Джон Б.; Кац, Виктор Дж. (2003), Первый курс абстрактной алгебры , Аддисон-Уэсли, ISBN 978-1-292-02496-7

[3] Как это часто бывает, но не всегда, один и тот же символ для обозначения работы обоих $A$ и $B$ здесь использовался.

[12] Символ ∗ обозначает операцию звезды Клини , а Σ ^∗ обозначает набор слов, образованных из алфавита Σ, включая пустое слово. Сопоставление терминов означает конкатенацию . Например, h ( u ) h ( v ) обозначает объединение h ( u ) с h ( v ).

[14] Нас уверяют, что языковой гомоморфизм h отображает пустое слово ε в пустое слово. Поскольку час ( ε ) = час ( ε ) = час ( ε ) час ( ε ), количество w символов в h ( ε ) равно числу 2 w символов в h ( ε ) h ( ε ). Следовательно, w = 0 и h ( ε ) имеет нулевую длину.

[1] Фрике, Роберт (1897–1912). Лекции по теории автоморфных функций . Б. Г. Тойбнер. ОСЛК 29857037 .

[2] См.:
Риттер, Эрнст (1892). «Уникальные автоморфные формы нулевого пола, пересмотр и расширение теоремы Пуанкаре » . Математические анналы (на немецком языке). 41 :1-82. дои : 10.1007/BF01443449 . S2CID 121524108 . Из сноски на стр. 22 : «Я хочу следовать предложению проф. Клейна вместо громоздких и не всегда достаточных терминов: «голоэдрический, или. гемиэдрические и т. д. изоморфные» ограничивают обозначение «изоморфные» случаем голоэдрического изоморфизма двух групп, а в противном случае говорят о «гомоморфизме»,...» (Следуя предложению проф. Клейна, вместо громоздкого и не громоздкого всегда удовлетворительные обозначения «голоэдрический, или полуэдрический и т. д. изоморфный», я ограничу наименование «изоморфный» случаем голоэдрического изоморфизма двух групп, однако в противном случае [я буду] говорить о «гомоморфизме»,…)
Фрике, Роберт (1892). «Об арифметическом характере функций треугольника, принадлежащих точкам ветвления (2,3,7) и (2,4,7)». Математические анналы (на немецком языке). 41 (3): 443–468. дои : 10.1007/BF01443421 . S2CID 120022176 . Из стр. 466: «Как видно непосредственно, это устанавливает гомоморфное*) отношение группы Г ₍₆₃₎ к группе мод. п неконгруэнтных замен с целыми рациональными коэффициентами определителя 1». (Таким образом, как сразу видно, гомоморфное отношение группы Г ₍₆₃₎ основано на группе неконгруэнтных по модулю n подстановок с целыми рациональными коэффициентами определителя 1.) Из сноски на с. 466: «*) Следуя обычаю, введенному г-ном Клейном в его последних лекциях, я пишу более подходящий «гомоморфизм» вместо прежнего термина «мероэдральный изоморфизм».» (Следуя использованию, введенному г-ном Кляйном в его последних лекциях, я пишу вместо прежнего обозначения «мероэдральный изоморфизм» более логичное «гомоморфизм».)

[6] Риттер, Эрнст (1892). «Уникальные автоморфные формы нулевого пола, пересмотр и расширение теоремы Пуанкаре » . Математические анналы (на немецком языке). 41 :1-82. дои : 10.1007/BF01443449 . S2CID 121524108 . Из сноски на стр. 22 : «Я хочу следовать предложению проф. Клейна вместо громоздких и не всегда достаточных терминов: «голоэдрический, или. гемиэдрические и т. д. изоморфные» ограничивают обозначение «изоморфные» случаем голоэдрического изоморфизма двух групп, а в противном случае говорят о «гомоморфизме»,...» (Следуя предложению проф. Клейна, вместо громоздкого и не громоздкого всегда удовлетворительные обозначения «голоэдрический, или полуэдрический и т. д. изоморфный», я ограничу наименование «изоморфный» случаем голоэдрического изоморфизма двух групп, однако в противном случае [я буду] говорить о «гомоморфизме»,…)

[7] Фрике, Роберт (1892). «Об арифметическом характере функций треугольника, принадлежащих точкам ветвления (2,3,7) и (2,4,7)». Математические анналы (на немецком языке). 41 (3): 443–468. дои : 10.1007/BF01443421 . S2CID 120022176 . Из стр. 466: «Как видно непосредственно, это устанавливает гомоморфное*) отношение группы Г ₍₆₃₎ к группе мод. п неконгруэнтных замен с целыми рациональными коэффициентами определителя 1». (Таким образом, как сразу видно, гомоморфное отношение группы Г ₍₆₃₎ основано на группе неконгруэнтных по модулю n подстановок с целыми рациональными коэффициентами определителя 1.) Из сноски на с. 466: «*) Следуя обычаю, введенному г-ном Клейном в его последних лекциях, я пишу более подходящий «гомоморфизм» вместо прежнего термина «мероэдральный изоморфизм».» (Следуя использованию, введенному г-ном Кляйном в его последних лекциях, я пишу вместо прежнего обозначения «мероэдральный изоморфизм» более логичное «гомоморфизм».)

[Birkhoff.1967-4] Jump up to: ^а ^б ^с ^д ^и Биркгоф, Гарретт (1967) [1940], Теория решетки , Публикации коллоквиума Американского математического общества, том. 25 (3-е изд.), Провиденс, Род-Айленд: Американское математическое общество , ISBN. 978-0-8218-1025-5 , МР 0598630

[Burris.Sankappanavar.2012-5] Jump up to: ^а ^б ^с Стэнли Н. Беррис; HP Санкаппанавар (2012). Курс универсальной алгебры (PDF) . С. Беррис и Х. П. Санкаппанавар. ISBN 978-0-9880552-0-9 .

[workmath-6] Jump up to: ^а ^б ^с Мак Лейн, Сондерс (1971). Категории для работающего математика . Тексты для аспирантов по математике . Том. 5. Шпрингер-Верлаг . Упражнение 4 в разделе I.5. ISBN 0-387-90036-5 . Збл 0232.18001 .

[7] Линдерхольм, CE (1970). Групповой эпиморфизм сюръективен. Американский математический ежемесячник , 77 (2), 176–177.

[8] Даскалеску, Сорин; Нэстасеску, Константин; Райану, Шербан (2001). Алгебра Хопфа: Введение . Чистая и прикладная математика. Том 235. Нью-Йорк, Нью-Йорк: Марсель Деккер. стр. 363. ISBN 0824704819 . Збл 0962.16026 .

[9] Подробное обсуждение реляционных гомоморфизмов и изоморфизмов см. в разделе 17.3, в Gunther Schmidt , 2010. Relational Mathematics . Издательство Кембриджского университета, ISBN 978-0-521-76268-7

[10] Сеймур Гинзбург , Алгебраические и теоретико-автоматные свойства формальных языков , Северная Голландия, 1975, ISBN 0-7204-2506-9 ,

[11] Т. Харью, Дж. Кархумеки, Морфизмы в Справочнике по формальным языкам , Том I, под редакцией Г. Розенберга, А. Саломаа, Springer, 1997, ISBN 3-540-61486-9 .

[13] Воин (2006) с. 287

[1]

[2]

[примечание 1]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[примечание 2]

[11]

[примечание 3]