Аналитическое продолжение

В комплексном анализе , разделе математики , аналитическое продолжение — это метод расширения области определения данной аналитической функции . Аналитическое продолжение часто позволяет определить дальнейшие значения функции, например, в новой области, где представление бесконечной серии , первоначально определявшей функцию, начинает расходиться .

Однако метод поэтапного продолжения может столкнуться с трудностями. Они могут иметь по существу топологическую природу, что приводит к несогласованности (определению более одного значения). Альтернативно они могут быть связаны с наличием сингулярностей . Случай нескольких комплексных переменных совершенно иной, поскольку тогда особенности не обязательно должны быть изолированными точками, и его исследование было основной причиной развития пучковых когомологий .

Первоначальное обсуждение

Аналитическое продолжение натурального логарифма (мнимая часть)

Предположим, f — аналитическая функция , определенная на непустом открытом подмножестве U комплексной плоскости. $\mathbb {C}$. Если V — большее открытое подмножество $\mathbb {C}$, содержащий U , и F — аналитическая функция, определенная на V такая, что

$F(z)=f(z)\qquad \forall z\in U,$

тогда F называется аналитическим продолжением f . Другими словами, ограничение F с на U — это функция f, которой мы начали.

Аналитические продолжения единственны в следующем смысле: если V — связная область определения двух аналитических функций F ₁ и F ₂ такая, что U содержится в V и для всех z в U

$F_{1}(z)=F_{2}(z)=f(z),$

затем

$F_{1}=F_{2}$

всём В. на Это связано с тем, что F ₁ − F ₂ — аналитическая функция, которая обращается в нуль в открытой связной области U функции f и, следовательно, должна обращаться в нуль во всей своей области. Это следует непосредственно из теоремы тождества для голоморфных функций .

Приложения

Обычный способ определения функций в комплексном анализе заключается в том, что сначала указывается функция только в небольшой области, а затем расширяется ее путем аналитического продолжения.

На практике это продолжение часто осуществляется путем установления некоторого функционального уравнения в небольшой области, а затем использования этого уравнения для расширения области. Примерами являются дзета-функция Римана и гамма-функция .

Концепция универсального накрытия была впервые разработана для определения естественной области аналитического продолжения аналитической функции . Идея найти максимальное аналитическое продолжение функции, в свою очередь, привела к развитию идеи римановых поверхностей .

Аналитическое продолжение используется в римановых многообразиях , решениях уравнений Эйнштейна . Например, аналитическое продолжение координат Шварцшильда в координаты Крускала – Секереса .

Рабочий пример

Аналитическое продолжение от U (с центром 1) до V (с центром a=(3+i)/2)

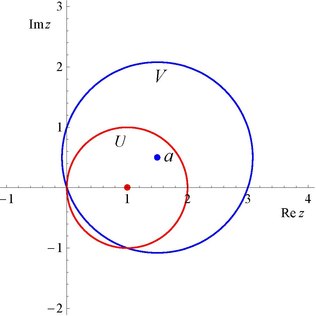
Начните с конкретной аналитической функции $f$. В данном случае он задается степенным рядом с центром в точке. $z=1$:

$$f(z)=\sum _{k=0}^{\infty }(-1)^{k}(z-1)^{k}.$$

По теореме Коши–Адамара его радиус сходимости равен 1. То есть, $f$ определен и аналитичен на открытом множестве $U=\{|z-1|<1\}$ который имеет границу $\partial U=\{|z-1|=1\}$. Действительно, ряд расходится при $z=0\in \partial U$.

Притворись, что мы этого не знаем $f(z)=1/z$и сосредоточимся на центрировании степенного ряда в другой точке $a\in U$:

$$f(z)=\sum _{k=0}^{\infty }a_{k}(z-a)^{k}.$$

Мы рассчитаем $a_{k}$и определим, сходится ли этот новый степенной ряд в открытом множестве $V$ который не содержится в $U$. Если да, то мы аналитически продолжим $f$ в регион $U\cup V$ что строго больше, чем $U$.

Расстояние от $a$ к $\partial U$ является $\rho =1-|a-1|>0$. Брать $0<r<\rho$; позволять $D$ быть диском радиуса $r$ вокруг $a$; и пусть $\partial D$ быть его границей. Затем $D\cup \partial D\subset U$. Используя формулу дифференцирования Коши для расчета новых коэффициентов, имеем $${\begin{aligned}a_{k}&={\frac {f^{(k)}(a)}{k!}}\\&={\frac {1}{2\pi i}}\int _{\partial D}{\frac {f(\zeta )d\zeta }{(\zeta -a)^{k+1}}}\\&={\frac {1}{2\pi i}}\int _{\partial D}{\frac {\sum _{n=0}^{\infty }(-1)^{n}(\zeta -1)^{n}d\zeta }{(\zeta -a)^{k+1}}}\\&={\frac {1}{2\pi i}}\sum _{n=0}^{\infty }(-1)^{n}\int _{\partial D}{\frac {(\zeta -1)^{n}d\zeta }{(\zeta -a)^{k+1}}}\\&={\frac {1}{2\pi i}}\sum _{n=0}^{\infty }(-1)^{n}\int _{0}^{2\pi }{\frac {(a+re^{i\theta }-1)^{n}rie^{i\theta }d\theta }{(re^{i\theta })^{k+1}}}\\&={\frac {1}{2\pi }}\sum _{n=0}^{\infty }(-1)^{n}\int _{0}^{2\pi }{\frac {(a-1+re^{i\theta })^{n}d\theta }{(re^{i\theta })^{k}}}\\&={\frac {1}{2\pi }}\sum _{n=0}^{\infty }(-1)^{n}\int _{0}^{2\pi }{\frac {\sum _{m=0}^{n}{\binom {n}{m}}(a-1)^{n-m}(re^{i\theta })^{m}d\theta }{(re^{i\theta })^{k}}}\\&={\frac {1}{2\pi }}\sum _{n=0}^{\infty }(-1)^{n}\sum _{m=0}^{n}{\binom {n}{m}}(a-1)^{n-m}r^{m-k}\int _{0}^{2\pi }e^{i(m-k)\theta }d\theta \\&={\frac {1}{2\pi }}\sum _{n=k}^{\infty }(-1)^{n}{\binom {n}{k}}(a-1)^{n-k}\int _{0}^{2\pi }d\theta \\&=\sum _{n=k}^{\infty }(-1)^{n}{\binom {n}{k}}(a-1)^{n-k}\\&=(-1)^{k}\sum _{m=0}^{\infty }{\binom {m+k}{k}}(1-a)^{m}\\&=(-1)^{k}a^{-k-1}\end{aligned}}.$$

Последнее суммирование является результатом k- го вывода геометрической прогрессии , что дает формулу $${\frac {1}{(1-x)^{k+1}}}=\sum _{m=0}^{\infty }{\binom {m+k}{k}}x^{m}.$$

Затем, $${\begin{aligned}f(z)&=\sum _{k=0}^{\infty }a_{k}(z-a)^{k}\\&=\sum _{k=0}^{\infty }(-1)^{k}a^{-k-1}(z-a)^{k}\\&={\frac {1}{a}}\sum _{k=0}^{\infty }\left(1-{\frac {z}{a}}\right)^{k}\\&={\frac {1}{a}}{\frac {1}{1-\left(1-{\frac {z}{a}}\right)}}\\&={\frac {1}{z}}\\&={\frac {1}{(z+a)-a}}\end{aligned}}$$

который имеет радиус сходимости $|a|$ вокруг $0$. Если мы выберем $a\in U$ с $|a|>1$, затем $V$ не является подмножеством $U$ и на самом деле больше по площади, чем $U$. На графике показан результат для $a={\tfrac {1}{2}}(3+i).$

Можем продолжить процесс: выбираем $b\in U\cup V$, отцентрируйте степенной ряд в $b$и определите, где сходится новый степенной ряд. Если в регионе есть точки, не входящие в $U\cup V$, то мы аналитически продолжим $f$ даже дальше. Этот конкретный $f$ можно аналитически продолжить на всю проколотую комплексную плоскость $\mathbb {C} \setminus \{0\}.$

В данном конкретном случае полученные значения $f(-1)$ одинаковы, когда последовательные центры имеют положительную мнимую часть или отрицательную мнимую часть. Это не всегда так; в частности, это не относится к комплексному логарифму , первообразной вышеуказанной функции.

Формальное определение микроба

Определенный ниже степенной ряд обобщается идеей ростка . Общая теория аналитического продолжения и ее обобщения известны как теория пучков . Позволять

$f(z)=\sum _{k=0}^{\infty }\alpha _{k}(z-z_{0})^{k}$

— степенной ряд , сходящийся в круге D _r ( z ₀ ), r > 0, определяемый формулой

$D_{r}(z_{0})=\{z\in \mathbb {C} :|z-z_{0}|<r\}$.

максимальное такое r Заметим, что без ограничения общности здесь и далее мы всегда будем считать, что выбрано , даже если оно равно ∞. Также обратите внимание, что было бы эквивалентно начать с аналитической функции, определенной на некотором небольшом открытом множестве. Мы говорим, что вектор

$g=(z_{0},\alpha _{0},\alpha _{1},\alpha _{2},\ldots )$

является зародышем f ​ . Основание вершина g ₀ группы g — это z ₀ , основа g это — это (α ₀ , α ₁ , α ₂ , ...), а g 1 _группы g — α ₀ . Вершина g — это значение f в точке z ₀ .

Любой вектор g = ( z ₀ , α ₀ , α ₁ , ...) является ростком, если он представляет собой степенной ряд аналитической функции вокруг z ₀ с некоторым радиусом сходимости r > 0. Поэтому можно смело говорить о набор микробов ${\mathcal {G}}$.

Топология множества ростков

Пусть g и h — ростки . Если $|h_{0}-g_{0}|<r$ где r — радиус сходимости g , и если степенной ряд, определенный g и h, задает идентичные функции на пересечении двух областей, то мы говорим, что h порождается g (или совместим с ним) , и пишем g ≥ ч . Это условие совместимости не является ни транзитивным, ни симметричным, ни антисимметричным. Если мы расширим отношение за счет транзитивности , мы получим симметричное отношение, которое, следовательно, также является отношением эквивалентности на ростках (но не упорядочиванием). Это расширение посредством транзитивности является одним из определений аналитического продолжения. Отношение эквивалентности будем обозначать $\cong$.

Мы можем определить топологию на ${\mathcal {G}}$. Пусть r > 0 и пусть

$U_{r}(g)=\{h\in {\mathcal {G}}:g\geq h,|g_{0}-h_{0}|<r\}.$

Множества U _r ( g ) для всех r > 0 и $g\in {\mathcal {G}}$ определить основу открытых множеств для топологии на ${\mathcal {G}}$.

компонент Связный ​ ${\mathcal {G}}$ (т. е. класс эквивалентности) называется пучком . Отметим также, что отображение, определяемое формулой $\phi _{g}(h)=h_{0}:U_{r}(g)\to \mathbb {C} ,$ где r — радиус схождения g , — карта . Набор таких диаграмм атлас образует ${\mathcal {G}}$, следовательно ${\mathcal {G}}$ является римановой поверхностью . ${\mathcal {G}}$ иногда называют универсальной аналитической функцией .

Примеры аналитического продолжения

$L(z)=\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}}{k}}(z-1)^{k}$

представляет собой степенной ряд, соответствующий натуральному логарифму вблизи z = 1. Этот степенной ряд можно превратить в росток

$g=\left(1,0,1,-{\frac {1}{2}},{\frac {1}{3}},-{\frac {1}{4}},{\frac {1}{5}},-{\frac {1}{6}},\ldots \right)$

Этот росток имеет радиус сходимости 1, поэтому пучок S. ему соответствует Это пучок функции логарифма.

Теорема единственности аналитических функций распространяется и на пучки аналитических функций: если пучок аналитической функции содержит нулевой росток (т. е. пучок равномерно равен нулю в некоторой окрестности), то весь пучок равен нулю. Вооружившись этим результатом, мы можем увидеть, что если мы возьмем любой росток g пучка S функции логарифма, как описано выше, и превратим его в степенной ряд f ( z ), то эта функция будет обладать свойством, что exp( f ( z )) знак равно z . Если бы мы решили использовать версию теоремы об обратной функции для аналитических функций, мы могли бы построить множество обратных для экспоненциального отображения, но мы бы обнаружили, что все они представлены некоторым ростком S. из В этом смысле S является «единственной истинной инверсией» экспоненциального отображения.

В более старой литературе пучки аналитических функций назывались многозначными функциями . См. связку для получения общей концепции.

Урочище

Предположим, что степенной ряд имеет радиус сходимости r и определяет аналитическую функцию f внутри этого круга. Рассмотрим точки на окружности сходимости. Точка, для которой существует окрестность, на которой f имеет аналитическое расширение, является регулярной , в противном случае сингулярной . Окружность является естественной границей, если все ее точки особые.

В более общем смысле, мы можем применить это определение к любой открытой связной области, в которой f является аналитической, и классифицировать точки границы области как регулярные или особые: тогда граница области является естественной границей, если все точки являются особыми, в которых случае, когда область является областью голоморфности .

Пример I: функция с естественной границей в нуле (простая дзета-функция).

Для $\Re (s)>1$ мы определяем так называемую простую дзета-функцию , $P(s)$, быть

$P(s):=\sum _{p\ {\text{ prime}}}p^{-s}.$

Эта функция аналогична суммирующей форме дзета-функции Римана, когда $\Re (s)>1$ поскольку это та же самая суммирующая функция, что и $\zeta (s)$, за исключением индексов, ограниченных только простыми числами, вместо суммирования всех положительных натуральных чисел . Простая дзета-функция имеет аналитическое продолжение на все комплексные s такие, что $0<\Re (s)<1$, что следует из выражения $P(s)$ логарифмами дзета-функции Римана как

$P(s)=\sum _{n\geq 1}\mu (n){\frac {\log \zeta (ns)}{n}}.$

С $\zeta (s)$ имеет простой несъемный шест на $s:=1$, тогда можно увидеть, что $P(s)$ имеет простой полюс в $s:={\tfrac {1}{k}},\forall k\in \mathbb {Z} ^{+}$. Поскольку множество точек

$\operatorname {Sing} _{P}:=\left\{k^{-1}:k\in \mathbb {Z} ^{+}\right\}=\left\{1,{\frac {1}{2}},{\frac {1}{3}},{\frac {1}{4}},\ldots \right\}$

имеет точку накопления 0 (предел последовательности как $k\mapsto \infty$), мы видим, что ноль образует естественную границу для $P(s)$. Это означает, что $P(s)$ не имеет аналитического продолжения для s слева от нуля (или в точке), т.е. продолжение невозможно для $P(s)$ когда $0\geq \Re (s)$. В качестве примечания: этот факт может быть проблематичным, если мы выполняем комплексный контурный интеграл на интервале, действительные части которого симметричны относительно нуля, скажем $I_{F}\subseteq \mathbb {C} \ {\text{such that}}\ \Re (s)\in (-C,C),\forall s\in I_{F}$ для некоторых $C>0$, где подынтегральная функция — функция, знаменатель которой зависит от $P(s)$ существенным образом.

Пример II: Типичный лакунарный ряд (естественная граница как подмножества единичного круга)

Для целых чисел $c\geq 2$, определим лакунарный ряд порядка c разложением в степенной ряд

${\mathcal {L}}_{c}(z):=\sum _{n\geq 1}z^{c^{n}},|z|<1.$

Очевидно, поскольку $c^{n+1}=c\cdot c^{n}$ существует функциональное уравнение для ${\mathcal {L}}_{c}(z)$ для любого z, удовлетворяющего $|z|<1$ данный ${\mathcal {L}}_{c}(z)=z^{c}+{\mathcal {L}}_{c}(z^{c})$. Также нетрудно видеть, что для любого целого числа $m\geq 1$, мы имеем еще одно функциональное уравнение для ${\mathcal {L}}_{c}(z)$ данный

${\mathcal {L}}_{c}(z)=\sum _{i=0}^{m-1}z^{c^{i}}+{\mathcal {L}}_{c}(z^{c^{m}}),\forall |z|<1.$

Для любых положительных натуральных чисел c функция лакунарного ряда расходится при $z=1$. Рассмотрим вопрос об аналитическом продолжении ${\mathcal {L}}_{c}(z)$ к другому комплексному z такому, что $|z|>1.$ Как мы увидим, для любого $n\geq 1$, функция ${\mathcal {L}}_{c}(z)$ расходится втот $c^{n}$-ые корни единства. Следовательно, поскольку множество, образованное всеми такими корнями, плотно на границе единичного круга, аналитического продолжения не существует. ${\mathcal {L}}_{c}(z)$ к комплексу z, модуль которого больше единицы.

Доказательство этого факта обобщается из стандартного рассуждения для случая, когда $c:=2.$ А именно, для целых чисел $n\geq 1$, позволять

${\mathcal {R}}_{c,n}:=\left\{z\in \mathbb {D} \cup \partial {\mathbb {D} }:z^{c^{n}}=1\right\},$

где $\mathbb {D}$ обозначает открытый единичный диск в комплексной плоскости и $|{\mathcal {R}}_{c,n}|=c^{n}$, то есть существуют $c^{n}$ различные комплексные числа z , лежащие на единичном круге или внутри него, такие, что $z^{c^{n}}=1$. Теперь ключевой частью доказательства является использование функционального уравнения для ${\mathcal {L}}_{c}(z)$ когда $|z|<1$ чтобы показать это

$\forall z\in {\mathcal {R}}_{c,n},\qquad {\mathcal {L}}_{c}(z)=\sum _{i=0}^{c^{n}-1}z^{c^{i}}+{\mathcal {L}}_{c}(z^{c^{n}})=\sum _{i=0}^{c^{n}-1}z^{c^{i}}+{\mathcal {L}}_{c}(1)=+\infty .$

Таким образом, для любой дуги на границе единичной окружности существует бесконечное число точек z внутри этой дуги таких, что ${\mathcal {L}}_{c}(z)=\infty$. Это условие эквивалентно утверждению, что окружность $C_{1}:=\{z:|z|=1\}$ образует естественную границу для функции ${\mathcal {L}}_{c}(z)$ для любого фиксированного выбора $c\in \mathbb {Z} \quad c>1.$ Следовательно, аналитического продолжения этих функций за пределы единичного круга не существует.

Теорема о монодромии

Основная статья: Теорема монодромии

Теорема монодромии дает достаточное условие существования прямого аналитического продолжения (т. е. продолжения аналитической функции до аналитической функции на большем множестве).

Предполагать $D\subset \mathbb {C}$ — открытое множество, а f — функция на D. аналитическая Если G — односвязная область, содержащая D , такая, что f имеет аналитическое продолжение вдоль каждого пути в G начиная с некоторой фиксированной точки a в D , то f имеет прямое аналитическое продолжение в G. ,

На приведенном выше языке это означает, что если G — односвязная область, а S пучок, множество базовых точек которого содержит G , то существует аналитическая функция f на G , ростки которой принадлежат S. —

Теорема Адамара о разрыве

Основная статья: Теорема Островского – Адамара о разрыве

Для степенного ряда

$f(z)=\sum _{k=0}^{\infty }a_{k}z^{n_{k}}$

с

$\liminf _{k\to \infty }{\frac {n_{k+1}}{n_{k}}}>1$

круг схождения является естественной границей. Такой степенной ряд называется лакунарным .Эта теорема была существенно обобщена Ойгеном Фабри (см. теорему о пробеле Фабри ) и Джорджем Полиа .

Теорема Полиа

Позволять

$f(z)=\sum _{k=0}^{\infty }\alpha _{k}(z-z_{0})^{k}$

— степенной ряд, то существует ε _k ∈ {−1, 1} такое, что

$f(z)=\sum _{k=0}^{\infty }\varepsilon _{k}\alpha _{k}(z-z_{0})^{k}$

имеет диск сходимости f вокруг z ₀ в качестве естественной границы.

Доказательство этой теоремы использует теорему Адамара о разрыве.

Полезная теорема: достаточное условие аналитического продолжения до неположительных целых чисел.

В большинстве случаев, если существует аналитическое продолжение комплексной функции, оно задается интегральной формулой. Следующая теорема, при условии выполнения ее гипотез, дает достаточное условие, при котором мы можем продолжить аналитическую функцию от ее точек схождения вдоль положительных действительных чисел до произвольной $s\in \mathbb {C}$ (за исключением конечного числа полюсов). Более того, формула дает явное представление значений продолжения неположительных целых чисел, выраженных точно через производные более высокого порядка (целые) исходной функции, оцененной в нуле.

Гипотезы теоремы

Мы требуем, чтобы функция $F:\mathbb {R} ^{+}\to \mathbb {C}$ удовлетворяет следующим условиям для применения сформулированной ниже теоремы о продолжении этой функции:

• (Т-1). Функция должна иметь непрерывные производные всех порядков, т. е. $F\in {\mathcal {C}}^{\infty }(\mathbb {R} ^{+})$. Другими словами, для любых целых чисел $j\geq 1$, интегральный порядок $j^{th}$ производная $F^{(j)}(x)={\frac {d^{(j)}}{dx^{(j)}}}[F(x)]$ должен существовать, быть непрерывным $\mathbb {R} ^{+}$, и сам быть дифференцируемым , так что все производные высшего порядка от F являются гладкими функциями x на положительных действительных числах;
• (Т-2). Потребуем, чтобы функция F , быстро убывала т.е. для всех $n\in \mathbb {Z} ^{+}$ мы получаем предельное поведение, которое $t^{n}F(t)\to 0$ поскольку t становится неограниченным, стремясь к бесконечности;
• (Т-3). обратное гамма-масштабирование) Преобразование Меллина ( F существует для всех комплексов s таких, что $\Re (s)>0$ за исключением $s\in \{\zeta _{1}(F),\zeta _{2}(F),\ldots ,\zeta _{k}(F)\}$ (или для всех s с положительными действительными частями, за исключением, возможно, конечного числа исключительных полюсов):

${\widetilde {\mathcal {M}}}[F](s):={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }t^{s}F(t){\frac {dt}{t}},\qquad \left|{\widetilde {\mathcal {M}}}[F](s)\right|\in (-\infty ,+\infty ),\forall s\in \{z\in \mathbb {C} :\Re (z)>0\}\setminus \{\zeta _{1}(F),\ldots ,\zeta _{k}(F)\}.$

Заключение теоремы

Пусть F — любая функция, определенная на положительных числах, которая удовлетворяет всем условиям (T1)–(T3), указанным выше. Тогда интегральное представление масштабированного преобразования Меллина F в точке s , обозначаемое ${\widetilde {\mathcal {M}}}[F](s)$, имеет мероморфное продолжение на комплексную плоскость $\mathbb {C} \setminus \{\zeta _{1}(F),\ldots ,\zeta _{k}(F)\}$. Более того, мы имеем это для любого неотрицательного $n\in \mathbb {Z}$, продолжение F в точке $s:=-n$ задается явно формулой

${\widetilde {\mathcal {M}}}[F](-n)=(-1)^{n}\times F^{(n)}(0)\equiv (-1)^{n}\times {\frac {\partial ^{n}}{{\partial x}^{n}}}\left[F(x)\right]|_{x=0}.$

Примеры

Пример I: Связь дзета-функции Римана с числами Бернулли.

Мы можем применить теорему к функции

$F_{\zeta }(x):={\frac {x}{e^{x}-1}}=\sum _{n\geq 0}B_{n}{\frac {x^{n}}{n!}},$

что соответствует экспоненциальной производящей функции чисел Бернулли , $B_{n}$. Для $\Re (s)>1$, мы можем выразить $\zeta (s)={\widetilde {\mathcal {M}}}[F_{\zeta }](s)$, поскольку мы можем вычислить, что следующая интегральная формула для обратных степеней целых чисел $n\geq 1$ справедливо для s в этом диапазоне:

${\frac {1}{n^{s}}}={\frac {1}{\Gamma (s)}}\int _{0}^{+\infty }t^{s-1}e^{-nt}dt,\Re (s)>1.$

Теперь, поскольку подынтегральная функция последнего уравнения является равномерно непрерывной функцией t для каждого положительного целого числа n , у нас есть интегральное представление для $\zeta (s)$ в любое время $\Re (s)>1$ данный

$\zeta (s)=\sum _{n\geq 1}n^{-s}={\frac {1}{\Gamma (s)}}\int _{0}^{+\infty }\left(\sum _{n\geq 1}e^{-nt}\right)t^{s-1}dt={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }t^{s-1}{\frac {F_{\zeta }(t)}{t}}dt.$

Когда мы выполним интегрирование по частям в интеграл преобразования Меллина для этого $F_{\zeta }(x)$, мы также получаем соотношение, что

$\zeta (s)={\frac {1}{(s-1)}}{\widetilde {\mathcal {M}}}[F_{\zeta }](s-1).$

Более того, поскольку $e^{t}\gg t^{n}$ для любой фиксированной целочисленной степени полинома t мы удовлетворяем условию теоремы, которое требует, чтобы $\lim _{t\to +\infty }t^{n}\cdot F_{\zeta }(t),\forall n\in \mathbb {Z} ^{+}$. Стандартное применение теоремы Тейлора к обычной производящей функции чисел Бернулли показывает, что $F_{\zeta }^{(n)}(0)={\frac {B_{n}}{n!}}\times n!=B_{n}$. В частности, по сделанному выше наблюдению о смещении $s\mapsto s-1$и этих замечаний мы можем вычислить значения так называемых тривиальных нулей дзета ( -функции Римана для $\zeta (-2n)$) и рациональные отрицательные константы нечетного целого порядка, $\zeta (-(2n+1)),n\geq 0$, по формуле

$\zeta (-n)=-{\frac {1}{n+1}}{\widetilde {\mathcal {M}}}[F_{\zeta }](-n-1)={\frac {(-1)^{n}}{n+1}}F_{\zeta }^{(n+1)}(0)={\begin{cases}-{\frac {1}{2}},&n=0;\\\infty ,&n=1;\\(-1)^{n}{\frac {B_{n+1}}{n+1}},&n\geq 2.\end{cases}}$

Пример II: Интерпретация F как суммирующей функции некоторой арифметической последовательности.

Предположим, что F — гладкая, достаточно убывающая функция на положительных действительных числах, удовлетворяющая дополнительному условию

$\Delta [F](x-1)=F(x)-F(x-1)=:f(x),\forall x\in \mathbb {Z} ^{+}.$

Применительно к контексту теории чисел мы рассматриваем такой F как суммирующую функцию арифметической функции f ,

$F(x):={\sum _{n\geq x}}^{\prime }f(n)$

где мы берем $F(x)=0,\forall 0<x<1$ и штриховое обозначение предыдущей суммы соответствует стандартным соглашениям, используемым для формулировки теоремы Перрона :

$F_{f}(x):={\sum _{n\leq x}}^{\prime }f(n)={\begin{cases}\sum _{n\leq [x]}f(n),&x\in \mathbb {R} ^{+}\setminus \mathbb {Z} ;\\\sum _{n\leq x}f(n)-{\frac {f(x)}{2}},&x\in \mathbb {R} ^{+}\cap \mathbb {Z} .\end{cases}}$

Нас интересует аналитическое продолжение ДГФ функции f или, что то же самое, ряда Дирихле по f в точке s :

$D_{f}(s):=\sum _{n\geq 1}{\frac {f(n)}{n^{s}}}.$

Обычно мы имеем определенное значение абсциссы сходимости , $\sigma _{0,f}>0$, определенный так, что $D_{f}(s)$ абсолютно сходится для всех комплексов , удовлетворяющих $\Re (s)>\sigma _{0,f}$, и где $D_{f}(s)$ предполагается, что он имеет полюс $s:=\pm \sigma _{0,f}$ и так что исходный ряд Дирихле для $D_{f}(s)$ расходится для всех s таких, что $\Re (s)\leq \sigma _{0,f}$. Известно, что существует связь преобразования Меллина сумматорной функции любого f с продолжением его ДФР при $s\mapsto -s$ формы:

$D_{f}(s)={\mathcal {M}}[F](-s)=\int _{1}^{\infty }{\frac {F_{f}(s)}{x^{s+1}}}dx$

То есть при условии $D_{f}(s)$ имеет продолжение в комплексную плоскость слева от начала координат, мы можем выразить суммирующую функцию любого f с помощью обратного преобразования Меллина DGF f, продолженного до s с действительными частями меньше нуля, как:

$F_{f}(x)={\mathcal {M}}^{-1}\left[{\mathcal {M}}[F_{f}](-s)\right](x)={\mathcal {M}}^{-1}[D_{f}(-s)](x).$

Мы можем сформировать DGF, или производящую функцию Дирихле , любого предписанного f, учитывая нашу гладкую целевую функцию F, выполняя суммирование по частям как

${\begin{aligned}D_{f}(s)&={\frac {1}{\Gamma (s)}}\int _{0}^{+\infty }\left(\sum _{n\geq 1}(F(n)-F(n-1))e^{-nt}\right)t^{s}dt\\&={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }\lim _{N\to \infty }\left[F(N)e^{-Nt}+\sum _{k=0}^{N-1}F(k)e^{-kt}\left(1-e^{-t}\right)\right]dt\\&={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }t^{s-1}(1-e^{-t})\int _{0}^{\infty }F(r/t)e^{-r}drdt\\&={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }t^{s-1}\left(1-e^{-t}\right){\widetilde {F}}\left({\frac {1}{t}}\right)dt\\&={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }{\frac {\left(1-e^{-1/u}\right)}{u^{s}(1-u)}}F\left({\frac {u}{1-u}}\right)du,\end{aligned}}$

где ${\hat {F}}(x)\equiv {\mathcal {L}}[F](x)$ является преобразованием Лапласа-Бореля , которое F , если

$F(z):=\sum _{n\geq 0}{\frac {f_{n}}{n!}}z^{n}$

соответствует экспоненциальной производящей функции некоторой последовательности, нумерованной $f_{n}/n!=F^{(n)}(0)/n!$ (как предписано в ряд Тейлора разложением F около нуля), тогда

${\widetilde {F}}(z)=\sum _{n\geq 0}f_{n}z^{n}$

- это его обычная форма производящей функции над последовательностью, коэффициенты которой нумеруются как $[z^{n}]{\widetilde {F}}(z)\equiv f_{n}=F^{(n)}(0)$.

Отсюда следует, что если мы напишем

$G_{F}(x):={\frac {x}{1-x}}F\left({\frac {x}{1-x}}\right)=\sum _{n\geq 0}\left(\sum _{k=0}^{n}{\binom {n}{k}}[z^{k}]F(z)\right)x^{n+1},$

поочередно интерпретируется как знаковый вариант биномиального преобразования F , тогда мы можем выразить DGF как следующее преобразование Меллина в $-s$:

${\begin{aligned}D_{f}(s)&={\mathcal {M}}[G_{F}](-s){\mathcal {M}}\left[1-e^{-1/x}\right](-s)\\&={\frac {{\mathcal {M}}[G_{F}](-s)}{s-1}}\left(1-\Gamma (s)\right)\end{aligned}}$

Наконец, поскольку гамма-функция имеет мероморфное продолжение в $\mathbb {C} \setminus \mathbb {N}$, для всех $s\in \mathbb {C} \setminus \{0,1,2,\ldots \},$ мы имеем аналитическое продолжение ДГФ для f в -s вида

$D_{f}(-s)=-{\frac {1-\Gamma (-s)}{s+1}}{\mathcal {M}}[G_{F}](s),$

где формула для $D_{f}(-n)$ для целых неотрицательных чисел n определяется по формуле теоремы как

$D_{f}(-n)=(-1)^{n}{\frac {d^{n}}{{dx}^{n}}}\left[\left(1-e^{-1/x}\right){\frac {x}{1-x}}F\left({\frac {x}{1-x}}\right)\right]{\Biggr |}_{x=0}.$

Более того, при условии, что арифметическая функция f удовлетворяет условию $f(1)\neq 1$ так что существует его обратная функция Дирихле, ДФР $f^{-1}$ продолжается до любого $s\in \mathbb {C} \cap \{z:\Re (z)\in (-\infty ,-\sigma _{0,f})\cup (\sigma _{0,f},+\infty )\}$, то есть любой комплексный s, за исключением s в f -определенной или зависящей от приложения f -специфичной, так называемой критической полосе между вертикальными линиями $z=\pm \sigma _{0,f}$, и значение этой обратной функции DGF, когда $\Re (s)<-\sigma _{0,f}$ дается

$D_{f^{-1}}(-s)={\begin{cases}0,&n\in \mathbb {N} ;\\-{\frac {s+1}{1-\Gamma (-s)}}{\mathcal {M}}[G_{F}^{-1}](s),&{\text{otherwise.}}\end{cases}}$

Чтобы продолжить ДГФ функции Дирихле, обратной к s внутри этой f -определенной критической полосы , нам необходимо некоторое знание функционального уравнения для ДФР: $D_{f}(s)$, что позволяет связать s так, что ряд Дирихле , определяющий эту функцию, изначально абсолютно сходится к значениям s внутри этой полосы — по сути, формула, обеспечивающая, что $D_{f}(s)=\xi _{f}(s)\times D_{f}(\sigma _{0,f}-s)$ необходимо определить ДГФ в этой полосе.

См. также

• Звезда Миттаг-Леффлера
• Голоморфное функциональное исчисление
• Численное аналитическое продолжение

Ссылки

• Ларс Альфорс (1979). Комплексный анализ (3-е изд.). МакГроу-Хилл. стр. 172, 284.
• Людвиг Бибербах (1955). Аналитическое продолжение . Издательство Спрингер.
• П. Динес (1957). Ряд Тейлора: введение в теорию функций комплексной переменной . Нью-Йорк: Dover Publications, Inc.

Внешние ссылки

• «Аналитическое продолжение» , Энциклопедия Математики , EMS Press , 2001 [1994]
• Аналитическое продолжение на MathPages
• Вайсштейн, Эрик В. «Аналитическое продолжение» . Математический мир .