Механизм

Шестерня ^{[ 1 ]}^{[ 2 ]} или шестерня ^{[ 3 ]}^{[ 4 ]}^{[ 5 ]} представляет собой вращающуюся часть машины, обычно используемую для передачи вращательного движения и/или крутящего момента посредством ряда зубьев, которые входят в зацепление с совместимыми зубьями другой шестерни или другой детали. Зубья могут представлять собой цельные выступы или полости, обработанные на детали, либо отдельные штифты, вставленные в нее. В последнем случае шестерню обычно называют зубчатой . Шестигранник колышков может быть одним из тех ^{[ 6 ]}^{[ 7 ]}^{[ 8 ]} или весь механизм. ^{[ 9 ]}^{[ 6 ]}^{[ 8 ]} Две или более шестерни, находящиеся в зацеплении, называются зубчатой передачей .

Меньший элемент пары зацепляющихся шестерен часто называют шестерней . Чаще всего шестерни и зубчатые передачи могут использоваться для обмена крутящего момента на скорость вращения между двумя осями или другими вращающимися частями и/или для изменения оси вращения и/или для изменения направления вращения. Зубчатое колесо также может использоваться для передачи линейной силы и/или линейного движения на рейку , прямой стержень с рядом совместимых зубьев.

Шестерни относятся к числу наиболее распространенных механических деталей. Они бывают самых разных форм и материалов и используются для множества различных функций и применений. могут варьироваться от нескольких мкм Диаметры в микромашинах . ^{[ 10 ]} от нескольких мм в часах и игрушках до более 10 метров в некотором горнодобывающем оборудовании. ^{[ 11 ]} Другие типы деталей, которые по форме и функциям чем-то похожи на шестерни, включают звездочку , которая предназначена для взаимодействия со звеньевой цепью вместо другой шестерни, и шкив ГРМ , предназначенный для сцепления с ремнем ГРМ . Большинство шестерен имеют круглую форму и одинаковые зубья, что обеспечивает максимально плавную работу; но есть несколько применений некруглых шестерен , а женевский привод по своей конструкции имеет крайне неравномерную работу.

Видны шестерни, представляющие собой экземпляры основного рычага «автомата». ^{[ 12 ]} Когда маленькая шестерня приводит в движение большую, механическое преимущество этого идеального рычага приводит крутящего момента T к увеличению скорости вращения ω , но к уменьшению . Противоположный эффект получается, когда большая шестерня приводит в движение маленькую. Изменения пропорциональны передаточному числу r , имеет значение передаточное число зубьев. а именно, T ₂ / T ₁ = r = N ₂ / N ₁ и ω ₂ / ω ₁ = 1/ r = N ₁ / N ₂ . В зависимости от геометрии пары направление вращения также может быть обратным (с по часовой стрелке на против часовой стрелки или наоборот).

Большинство транспортных средств имеют трансмиссию или «коробку передач», содержащую набор шестерен, которые могут соединяться в различных конфигурациях. Коробка передач позволяет оператору изменять крутящий момент, прикладываемый к колесам, без изменения частоты вращения двигателя. Редукторы используются также во многих других машинах, таких как токарные станки и ленточные конвейеры . Во всех этих случаях такие термины, как «первая передача», «высокая передача» и «задняя передача», относятся к общим передаточным числам крутящих моментов различных конфигураций зацепления, а не к конкретным физическим передачам. Эти термины могут применяться даже тогда, когда транспортное средство фактически не имеет передач, как в бесступенчатой трансмиссии . ^{[ 13 ]}

История

Самые ранние сохранившиеся шестерни датируются 4 веком до нашей эры в Китае. ^{[ 14 ]} (времена Чжань Го — Поздняя династия Восточного Чжоу ), которые сохранились в Лоянском музее провинции Хэнань, Китай .

В Европе Аристотель упоминает шестерни около 330 г. до н. э. в качестве колесных приводов в лебедках. Он заметил, что направление вращения меняется на противоположное, когда одно зубчатое колесо приводит в движение другое зубчатое колесо. Филон Византийский был одним из первых, кто применил шестерни в водоподъёмных устройствах. ^{[ 15 ]} Шестерни появляются в произведениях, связанных с Героем Александрийским , в Римском Египте около 50 г. н.э. ^{[ 16 ]} но их можно проследить до механики Александрийской библиотеки в III веке до н.э. в Птолемеевском Египте , и они были значительно развиты греческим эрудитом Архимедом (287–212 до н.э.). ^{[ 17 ]} Самые ранние сохранившиеся шестерни в Европе были найдены в Антикиферском механизме , примере очень раннего и сложного устройства с зубчатой передачей, предназначенного для расчета астрономических положений Солнца, Луны и планет, а также для предсказания затмений . Время его строительства сейчас оценивается между 150 и 100 годами до нашей эры. ^{[ 18 ]}^{[ 19 ]}^{[ 20 ]}

Китайский инженер Ма Цзюнь (ок. 200–265 гг. н. э.) описал колесницу, указывающую на юг . Набор дифференциальных шестерен, соединенных с колесами и указателем наверху колесницы, сохранял неизменным направление последней при повороте колесницы. ^{[ 21 ]}

Еще один ранний сохранившийся пример зубчатого механизма — сложное календарное устройство, показывающее фазу Луны, день месяца и места Солнца и Луны в Зодиаке, было изобретено в Византийской империи в начале VI века нашей эры. ^{[ 22 ]}^{[ 23 ]}

с редуктором Механические водяные часы были построены в Китае в 725 году нашей эры. ^{[ нужна ссылка ]}

Около 1221 года нашей эры астролябия была построена в Исфахане с приводом, показывающая положение Луны в зодиаке и ее фазу , а также количество дней после новолуния. ^{[ 24 ]}

Червячная передача была изобретена на Индийском субконтиненте для использования в роликовых хлопкоочистительных машинах где-то в XIII–XIV веках. ^{[ 25 ]}

Сложные астрономические часы, получившие название Астрариум , были построены между 1348 и 1364 годами Джованни Донди дель Орологио . У него было семь граней и 107 движущихся частей; на нем были показаны положения Солнца, Луны и пяти известных тогда планет, а также дни религиозных праздников. ^{[ 26 ]} Часы Солсберийского собора , построенные в 1386 году, являются старейшими в мире механическими часами с приводом, которые до сих пор работают.

Дифференциальные передачи были использованы британским часовщиком Джозефом Уильямсоном в 1720 году. ^{[ нужна ссылка ]}

Однако самые старые функционирующие механизмы были созданы природой и обнаружены в задних лапах нимф цикадки Issus coleoptratus .

Этимология

Слово снаряжение , вероятно, происходит от древнескандинавского gørvi (множественное число gørvar ) «одежда, снаряжение», связанного с gøra , gørva «изготовлять, строить, строить»; «навести порядок, подготовиться», распространенный глагол на древнескандинавском языке, «используется в самых разных ситуациях, от написания книги до разделки мяса». В этом контексте значение слова «зубчатое колесо в машинах» впервые появилось в 1520-х годах; конкретное механическое значение термина «части, с помощью которых двигатель передает движение» датируется 1814 годом; конкретно транспортного средства (велосипеда, автомобиля и т. д.) к 1888 г. ^{[ 27 ]}

Зубец – это зуб на колесе. От среднеанглийского cogge, от древнескандинавского (сравните норвежское kugg («шестеренка»), шведского kugg , kugge («шестеренка, зуб»)), от протогерманского * kuggō (сравните голландское kogge (« шестеренка »), немецкого Kock ) , от праиндоевропейского * gugā («горб, шар») (ср. литовское gugà («навершие, горб, холм»), от PIE * gēw- («сгибаться, выгибаться»). ^{[ 28 ]} Впервые использован c. 1300 в смысле «колесо с зубьями или зубцами»; конец 14 в., «зуб на колесе»; зубчатое колесо, начало 15в. ^{[ 29 ]}

Материалы

Шестерни антикиферского механизма изготовлены из бронзы , а самые ранние сохранившиеся китайские шестерни сделаны из железа. Эти металлы, а также олово , по сей день обычно используются для изготовления часов и подобных механизмов.

Исторически большие шестерни, например, используемые на мельницах , обычно делались из дерева, а не из металла. Это были зубчатые колеса, сделанные путем вставки ряда деревянных колышков или зубцов по ободу колеса. Зубцы часто делались из клена .

Деревянные шестерни постепенно были заменены изготовленными или металлическими, например, чугунными сначала , затем стальными и алюминиевыми . Чаще всего используется сталь из-за ее высокого соотношения прочности к весу и низкой стоимости. Алюминий не так прочен, как сталь при той же геометрии, но легче и его легче обрабатывать. порошковая металлургия может использоваться со сплавами, которые нелегко отлить или обработать.

Тем не менее, из-за стоимости или других соображений некоторые ранние металлические шестерни имели деревянные шестерни, каждый зуб образул своего рода специализированный «сквозной» паз и шиповое соединение. ^{[ 30 ]}

В последнее время конструкционные пластмассы и композитные материалы стали заменять металлы во многих областях применения, особенно при умеренных скоростях и крутящих моментах. Они не так прочны, как сталь, но дешевле, могут производиться серийно методом литья под давлением. ^{[ 31 ]} не нуждаются в смазке. Пластиковые шестерни могут даже быть намеренно спроектированы так, чтобы быть самой слабой частью механизма, чтобы в случае заклинивания они выйдут из строя первыми и, таким образом, избежат повреждения более дорогих деталей. Такие жертвенные шестерни могут быть более простой альтернативой другим устройствам защиты от перегрузки, таким как муфты и двигатели с ограничением крутящего момента или тока.

Несмотря на преимущества металла и пластика, дерево продолжало использоваться для изготовления больших шестерен еще пару столетий назад из-за стоимости, веса, традиций или других соображений. В 1967 году компания Thompson Manufacturing Company из Ланкастера, штат Нью-Гэмпшир, все еще вела очень активный бизнес по поставке десятков тысяч кленовых зубьев шестерен в год, в основном для использования на бумажных фабриках и мельницах , некоторые из которых были созданы более 100 лет назад. ^{[ 32 ]}

Производство

Наиболее распространенными методами изготовления зубчатых колес являются штампы , пескоструйное и литье по выплавляемым моделям ; литье под давлением ; порошковая металлургия ; гашение ; и зуборезка .

По состоянию на 2014 год около 80% всех зубчатых передач, производимых в мире, производится методом сетчатого формования. Литая зубчатая передача обычно изготавливается методом порошковой металлургии, литья пластмасс под давлением или литья под давлением металла. ^{[ 33 ]} Зубчатые колеса, изготовленные методом порошковой металлургии, часто требуют этапа спекания после извлечения из формы. Литые шестерни требуют зуборезки или другой механической обработки для придания зубцам необходимой точности. Наиболее распространенной формой зубонарезания является червячная обработка , но зубодолбежную обработку , фрезерование и протяжку вместо нее можно использовать .

Металлические шестерни, предназначенные для работы в тяжелых условиях, например, в трансмиссиях легковых и грузовых автомобилей, зубья подвергаются термической обработке , чтобы сделать их более твердыми и износостойкими, при этом сердечник остается мягким, но прочным . Для больших зубчатых колес, склонных к короблению, закалочный пресс применяют .

Шестерни можно изготовить с помощью 3D-печати ; однако этот вариант обычно используется только для прототипов или очень ограниченных производственных партий из-за его высокой стоимости, низкой точности и относительно низкой прочности получаемой детали.

Сравнение с другими механизмами привода

Помимо зубчатых передач, другие альтернативные методы передачи крутящего момента между несоосными деталями включают звенья цепей , приводимые в движение звездочками, фрикционные приводы , ремни и шкивы , гидравлические муфты и зубчатые ремни .

Одним из основных преимуществ зубчатых передач является то, что их жесткий корпус и плотное зацепление зубьев обеспечивают точное отслеживание вращения зубчатой передачи, ограниченное только люфтом и другими механическими дефектами. По этой причине их предпочитают в точных устройствах, таких как часы. Зубчатые передачи также могут иметь меньшее количество отдельных деталей (всего две) и иметь минимальные потери мощности, минимальный износ и длительный срок службы. Зубчатые передачи также часто являются наиболее эффективным и компактным способом передачи крутящего момента между двумя непараллельными осями.

С другой стороны, шестерни более дороги в производстве, могут требовать периодической смазки и могут иметь большую массу и инерцию вращения, чем эквивалентные шкивы. Что еще более важно, расстояние между осями согласованных шестерен ограничено и не может быть изменено после их изготовления. Существуют также приложения, в которых проскальзывание при перегрузке или переходных процессах (как это происходит с ремнями, гидравликой и фрикционными колесами) не только приемлемо, но и желательно.

Идеальная модель шестерни

Для целей базового анализа каждую шестерню можно идеализировать как абсолютно жесткое тело , которое при нормальной работе вращается вокруг оси вращения неподвижной в пространстве , не скользя вдоль нее. Таким образом, каждая точка шестерни может двигаться только по окружности, перпендикулярной ее оси и центрированной на ней. В любой момент t все точки шестерни будут вращаться вокруг этой оси с одинаковой угловой скоростью ω ( t ) в одном и том же смысле. Скорость не обязательно должна быть постоянной во времени.

Рабочая поверхность шестерни состоит из всех точек ее поверхности, которые при нормальной работе могут контактировать с согласующей шестерней с положительным давлением . Все остальные части поверхности не имеют значения (за исключением того, что их не может пересечь ни одна часть соответствующей шестерни). В шестерне с N зубьями рабочая поверхность имеет N -кратную вращательную симметрию относительно оси, то есть она конгруэнтна сама себе, когда шестерня поворачивается на 1/ N оборота.

Если передача предназначена для передачи или приема крутящего момента только в определенном направлении (по часовой стрелке или против часовой стрелки относительно некоторой исходной точки зрения), рабочая поверхность состоит из N отдельных участков, поверхности зубьев ; которые имеют одинаковую форму и одинаково расположены относительно оси, на расстоянии 1/ N оборота друг от друга.

Если крутящий момент на каждой шестерне может иметь оба направления, рабочая поверхность будет иметь два набора N зубьев; каждый набор будет эффективен только в том случае, если крутящий момент имеет одно конкретное значение, и два набора можно анализировать независимо от другого. Однако в этом случае шестерня обычно также имеет «перевернутую» симметрию, так что два набора поверхностей зубьев конгруэнтны после переворота шестерни. Такое расположение гарантирует, что две шестерни всегда надежно зафиксированы вместе, без люфта .

Во время работы каждая точка p каждой поверхности зуба в какой-то момент будет контактировать с поверхностью зуба согласующего колеса в некоторой точке q одной из его поверхностей зуба. В этот момент и в этих точках две грани должны иметь одинаковое перпендикулярное направление, но противоположную ориентацию. Но поскольку две шестерни вращаются вокруг разных осей, точки p и q движутся по разным окружностям; следовательно, контакт не может длиться более одного мгновения, и тогда p либо соскользнет по другой грани, либо вообще перестанет с ней контактировать.

С другой стороны, в любой данный момент существует по крайней мере одна такая пара точек контакта; обычно более одной, даже целой линии или поверхности контакта.

Реальные шестерни во многом отличаются от этой модели: они не являются идеально жесткими, их крепление не обеспечивает идеальной фиксации оси вращения в пространстве, зубья могут иметь несколько другую форму и расстояние, грани зубьев не идеально гладкие, и так далее. Тем не менее, эти отклонения от идеальной модели можно игнорировать при базовом анализе работы зубчатой передачи.

Относительное положение оси

Одним из критериев классификации шестерен является относительное положение и направление осей или вращения шестерен, которые должны быть зацеплены друг с другом.

Параллельно

В наиболее распространенной конфигурации оси вращения двух шестерен параллельны, и обычно их размеры таковы, что они соприкасаются вблизи точки между двумя осями. В этой конфигурации две шестерни вращаются в противоположных направлениях.

Иногда оси параллельны, но одна шестерня вложена в другую. В этой конфигурации обе шестерни вращаются в одном и том же направлении.

Если две шестерни пересечены воображаемой плоскостью, перпендикулярной осям, каждая секция одной шестерни будет взаимодействовать только с соответствующей секцией другой шестерни. Таким образом, трехмерную зубчатую передачу можно понимать как набор плоских и бесконечно тонких шестерен, то есть по существу двумерных.

Перекрещенный

В скрещенном расположении оси вращения двух шестерен не параллельны, а пересекаются под произвольным углом, кроме нуля или 180 градусов.

Для наилучшей работы каждое колесо должно представлять собой коническую шестерню , общая форма которой напоминает срез ( усеченный конус ) конуса , вершина которого является точкой встречи двух осей.

Конические шестерни с одинаковым количеством зубьев и осями вала, расположенными под углом 90 градусов, называются угловыми (США) или угловыми (Великобритания).

Независимо от угла между осями большее из двух неравных совмещенных конических колес может быть внутренним или внешним, в зависимости от желаемого относительного направления вращения. ^{[ 34 ]}

Если две шестерни разделены воображаемой сферой, центром которой является точка пересечения двух осей, каждая секция останется на поверхности этой сферы при вращении шестерни, а секция одной шестерни будет взаимодействовать только с соответствующей секцией шестерни. другая шестерня. Таким образом, пару зацепленных трехмерных шестерен можно понимать как стопку вложенных друг в друга бесконечно тонких чашеобразных шестерен.

Перекос

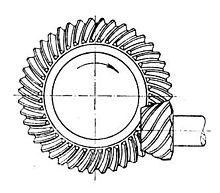
Шестерни в соответствующей паре называются перекошенными , если их оси вращения представляют собой косые линии — не параллельные и не пересекающиеся.

В этом случае наилучшей формой каждой шаговой поверхности является не цилиндрическая и не коническая, а часть гиперболоида вращения . ^{[ 35 ]}^{[ 36 ]} называются гипоидными Такие передачи сокращенно . Гипоидные передачи чаще всего встречаются с валами под углом 90 градусов.

Контакт между зубьями гипоидной шестерни может быть даже более плавным и постепенным, чем у зубьев спирально-конической шестерни, но также иметь скользящее действие вдоль зацепляющихся зубьев при вращении, и поэтому обычно требуются некоторые из наиболее вязких типов трансмиссионного масла, чтобы избежать его выдавливания. с сопрягаемых поверхностей зубьев масло обычно обозначается HP (от гипоидного масла), за которым следует число, обозначающее вязкость. Кроме того, шестерня может иметь меньше зубьев, чем спирально-коническая шестерня, в результате чего передаточное число 60:1 и выше становится возможным при использовании одного набора гипоидных шестерен. ^{[ 37 ]} Этот тип передачи наиболее распространен в трансмиссиях автомобилей вместе с дифференциалом . Хотя обычный (негипоидный) зубчатый венец подходит для многих применений, он не идеален для трансмиссии транспортных средств, поскольку создает больше шума и вибрации, чем гипоидный механизм. Вывод на рынок гипоидных передач для массового производства стал техническим достижением 1920-х годов.

Ориентация зубов

Внутренний и внешний

Зубчатое колесо называется внешним , если его зубья направлены вообще от оси вращения, и внутренним в противном случае. ^{[ 34 ]} В паре совпадающих колес только одно из них (большое) может быть внутренним.

Корона

Коронная шестерня или контратная шестерня — это шестерня, зубья которой выступают под прямым углом к плоскости. Коронная шестерня также иногда входит в зацепление со спусковым механизмом , например, в механических часах.

Направление резания зуба

Зубья шестерни обычно проходят по всей толщине шестерни. Еще одним критерием классификации шестерен является общее направление зубьев по этому измерению. На этот атрибут влияет относительное положение и направление осей или вращение шестерен, которые должны быть связаны друг с другом.

Прямой

В цилиндрической цилиндрической шестерне или прямозубой шестерне поверхности зубьев прямые в направлении, параллельном оси вращения. Любой воображаемый цилиндр с той же осью будет резать зубья по параллельным прямым.

Зубы могут быть как внутренними, так и внешними. Две цилиндрические шестерни правильно зацепляются друг с другом только в том случае, если они установлены на параллельных валах. ^{[ 38 ]} Нагрузки на зубья не создают осевого давления. Зубчатые передачи превосходны на умеренных скоростях, но имеют тенденцию быть шумными на высоких скоростях. ^{[ 39 ]}

Для устройств со скрещенными непараллельными осями грани в прямозубой передаче представляют собой части общей конической поверхности , образующие которой ( образующие ) проходят через точку встречи двух осей, в результате чего получается коническая передача . Такие передачи обычно используются только на скоростях ниже 5 м/с (1000 футов/мин) или, для небольших передач, 1000 об/мин. ^{[ 40 ]}

спиральный

В косозубой или сухой неподвижной передаче стенки зубьев не параллельны оси вращения, а расположены под углом. Воображаемая делительная поверхность (цилиндр, конус или гиперболоид, в зависимости от положения относительных осей) пересекает каждую грань зуба по дуге спирали . Косозубые шестерни могут зацепляться параллельно или в разных направлениях. Первое относится к тому, когда валы параллельны друг другу; это самая распространенная ориентация. В последнем валы непараллельны, и в этой конфигурации шестерни иногда называют «косыми шестернями».

Наклонные зубья входят в зацепление более плавно, чем зубья прямозубой шестерни, заставляя их работать более плавно и тихо. ^{[ 41 ]} В параллельных косозубых передачах каждая пара зубьев сначала входит в контакт в одной точке на одной стороне зубчатого колеса; движущаяся кривая контакта затем постепенно увеличивается по поверхности зуба до максимума, затем отступает до тех пор, пока зубы не нарушат контакт в одной точке на противоположной стороне. В прямозубых шестернях зубья внезапно встречаются на линии контакта по всей своей ширине, вызывая напряжение и шум. Прямозубые шестерни издают характерный визг на высоких оборотах. По этой причине прямозубые шестерни используются в низкоскоростных приложениях и в ситуациях, когда контроль шума не является проблемой, а косозубые шестерни используются в высокоскоростных приложениях, при передаче большой мощности или там, где снижение шума . важно ^{[ 42 ]} Скорость считается высокой, если скорость по тангажной линии превышает 25 м/с. ^{[ 43 ]}

Недостатком косозубых передач является результирующая тяга вдоль оси шестерни, которую необходимо компенсировать соответствующими упорными подшипниками . Однако эту проблему можно обойти, используя шестерню «елочка» или двойную косозубую передачу , которая не имеет осевой тяги – а также обеспечивает самовыравнивание шестерен. Это приводит к меньшему осевому усилию, чем у сопоставимой прямозубой шестерни.

Вторым недостатком косозубых передач также является более высокая степень трения скольжения между зацепляющимися зубьями, которую часто устраняют добавками в смазку.

При «перекрещенной» или «косой» конфигурации шестерни должны иметь одинаковый угол нажима и нормальный шаг; однако угол и направление спирали могут быть разными. Взаимосвязь между двумя валами фактически определяется углом(ами) спирали двух валов и направлением вращения, как определено: ^{[ 44 ]}

E=\beta _{1}+\beta _{2}

для шестерен одной руки,

E=\beta _{1}-\beta _{2}

для шестерен противоположного направления,

где $\beta$ - угол спирали зубчатого колеса. Скрещенная конфигурация менее механически надежна, поскольку между шестернями имеется только точечный контакт, тогда как в параллельной конфигурации имеется линейный контакт. ^{[ 44 ]}

Довольно часто используются косозубые шестерни, угол винтовой линии одной из которых отрицателен по сравнению с углом винтовой линии другой; такую пару можно также назвать имеющей правостороннюю спираль и левую спираль с равными углами. Два равных, но противоположных угла в сумме дают ноль: угол между валами равен нулю, то есть валы параллельны . Если сумма или разность (как описано в приведенных выше уравнениях) не равна нулю, валы пересекаются . Для валов, пересекающихся под прямым углом, углы спирали одинаковы, поскольку их сумма должна составлять 90 градусов. (Это относится к шестерням на рисунке выше: они правильно зацепляются в скрещенной конфигурации: для параллельной конфигурации один из углов винтовой линии должен быть изменен на противоположный. Показанные шестерни не могут зацепляться с параллельными валами.)

Двойная спираль

Двойные косозубые шестерни решают проблему осевого давления, возникающую в одинарных косозубых шестернях, за счет использования двойного набора зубьев, наклоненных в противоположных направлениях. Двойную косозубую шестерню можно представить как две зеркально расположенные косозубые шестерни, установленные близко друг к другу на общей оси. Такое расположение компенсирует чистую осевую силу, поскольку каждая половина шестерни действует в противоположном направлении, в результате чего чистая осевая сила равна нулю. Такое расположение также может устранить необходимость в упорных подшипниках. Однако двухкосозубые шестерни сложнее изготовить из-за их более сложной формы.

Шестерни «елочка» представляют собой особый тип косозубых передач. У них нет канавки посередине, как у некоторых других двухспиральных шестерен; две зеркально расположенные косозубые шестерни соединены так, что их зубья образуют V-образную форму. Это также может быть применено к коническим шестерням , как, например, в главной передаче Citroën Type A. Другой тип двойной косозубой передачи — это шестерня Вюста .

Для обоих возможных направлений вращения существуют два возможных варианта расположения противоположно ориентированных косозубых колес или поверхностей шестерен. Одно устройство называется стабильным, а другое неустойчивым. В стабильном расположении поверхности косозубого колеса ориентированы так, что каждая осевая сила направлена к центру колеса. В неустойчивой конструкции обе осевые силы направлены от центра шестерни. В любом случае общая (или чистая ) осевая сила на каждой шестерне равна нулю, если шестерни выровнены правильно. Если шестерни смещаются в осевом направлении, нестабильное устройство создает результирующую силу, которая может привести к разборке зубчатой передачи, тогда как стабильное устройство создает чистую корректирующую силу. Если направление вращения меняется на противоположное, направление осевых усилий также меняется на противоположное, поэтому стабильная конфигурация становится неустойчивой, и наоборот.

Стабильные двойные косозубые шестерни можно напрямую заменять прямозубыми без необходимости использования других подшипников.

Червь

Черви напоминают винты . Червяк находится в зацеплении с червячным колесом , которое похоже на прямозубую шестерню .

Червячные передачи — это простой и компактный способ добиться высокого крутящего момента при низкой скорости передачи. Например, косозубые передачи обычно ограничены передаточными числами менее 10:1, тогда как червячные передачи варьируются от 10:1 до 500:1. ^{[ 45 ]} Недостатком является возможность значительного скольжения, что приводит к низкой эффективности. ^{[ 46 ]}

Червячная передача — это разновидность косозубой передачи, но угол ее винтовой линии обычно несколько велик (около 90 градусов), а тело обычно довольно длинное в осевом направлении. Эти атрибуты придают ему качества, напоминающие винт. Разница между червяком и косозубой передачей заключается в том, что по крайней мере один зуб сохраняется для полного вращения вокруг спирали. Если это происходит, то это «червь»; если нет, то это «косозубая шестерня». У червя может быть всего один зуб. Если этот зуб сохраняется в течение нескольких оборотов вокруг спирали, на первый взгляд кажется, что у червя более одного зуба, но на самом деле мы видим один и тот же зуб, появляющийся через определенные промежутки времени по длине червя. Применяется обычная номенклатура винтов: однозубый червяк называется однозаходным или однозаходным ; червяк, имеющий более одного зуба, называется многозаходным или многозаходным . Угол спирали червяка обычно не указывается. Вместо этого дан угол подъема, равный 90 градусам минус угол винтовой линии.

В червячной передаче червяк всегда может приводить в движение шестерню. Однако, если шестерня попытается привести червяка в движение, это может или не удастся . В частности, если угол опережения мал, зубья шестерни могут просто зацепиться за зубья червяка, поскольку компонента силы по окружности червяка недостаточно для преодоления трения. Однако в традиционных музыкальных шкатулках шестерня приводит в движение червяк, имеющий большой угол спирали. Эта сетка приводит в движение лопатки ограничителя скорости, установленные на червячном валу.

Комплекты червячных передач, которые блокируются, называются самоблокирующимися , и это можно использовать с пользой, например, когда требуется установить положение механизма путем поворота червяка, а затем заставить механизм удерживать это положение. Примером может служить головка механизма , встречающаяся на некоторых типах струнных инструментов .

Если шестерня в червячном наборе представляет собой обычную косозубую передачу, достигается только одна точка контакта. ^{[ 37 ]}^{[ 47 ]} Если требуется передача мощности от средней до высокой, форма зубьев шестерни изменяется для достижения более тесного контакта за счет частичного охвата обеих шестерен друг друга. Это делается путем создания вогнутых частей и соединения их в седловой точке ; это называется конусный привод ^{[ 48 ]} или «Двойное конвертирование».

Червячные передачи могут быть правосторонними или левосторонними, следуя давно сложившейся практике для винтовой резьбы. ^{[ 34 ]}

Профиль зуба

Другим критерием классификации зубчатых колес является профиль зуба , форма поперечного сечения поверхности зуба воображаемым разрезом, перпендикулярным поверхности делителя, например, поперечная, нормальная или осевая плоскость.

Профиль зуба имеет решающее значение для плавности и равномерности движения соответствующих шестерен, а также для трения и износа.

кустарный

Зубья античных или кустарных шестерен, вырезанных вручную из листового материала, как и в антихитерском механизме, обычно имели простые профили, например треугольники. ^{[ 49 ]} Зубья более крупных шестерен, например, используемых в ветряных мельницах, обычно представляли собой колышки простой формы, такие как цилиндры, параллелепипеды или треугольные призмы, вставленные в гладкое деревянное или металлическое колесо; или же в таком колесе были вырезаны отверстия столь же простой формы.

Из-за неоптимального профиля эффективное передаточное число таких кустарных согласующих шестерен не было постоянным, а колебалось в течение каждого цикла зубьев, что приводило к вибрациям, шуму и ускоренному износу.

Клетка

, Зубчатая шестерня также называемая фонарной шестерней или фонарной шестерней, представляет собой одну из тех кустарных шестерен, которые имеют цилиндрические стержни вместо зубьев, параллельные оси и расположенные по кругу вокруг нее, так же, как стержни на круглой птичьей клетке или фонаре. Сборка скрепляется дисками на каждом конце, в которые установлены зубчатые стержни и ось. Шестерни с коробкой более эффективны, чем цельные шестерни. ^{[ нужна ссылка ]} и грязь может проваливаться сквозь стержни, а не застревать и увеличивать износ. Их можно изготовить с помощью очень простых инструментов, поскольку зубья формируются не путем резки или фрезерования, а путем сверления отверстий и вставки стержней.

Зубчатая передача, иногда используемая в часах, всегда должна приводиться в движение зубчатым колесом, а не использоваться в качестве привода. Консервативные производители часов изначально не одобряли зубчатый механизм. Он стал популярным в револьверных часах, где грязные условия труда были наиболее обычным явлением. Их часто использовали в отечественных американских часовых механизмах. ^{[ нужна ссылка ]}

Математический

В большинстве современных передач профиль зуба обычно не прямой и не круглый, а специальной формы, предназначенной для достижения постоянного передаточного числа угловых скоростей.

Существует бесконечное разнообразие профилей зубов, которые помогут достичь этой цели. Фактически, учитывая достаточно произвольную форму зуба, можно разработать профиль зуба для сопряженной шестерни, которая будет это делать.

Параллельные и скрещенные оси

Однако в настоящее время для зубчатых колес с параллельными или скрещенными осями чаще всего используются два профиля зубьев с постоянной скоростью, основанные на циклоидной и эвольвентной кривых.

Циклоидные шестерни были более распространены до конца 1800-х годов. С тех пор эвольвента во многом вытеснила ее, особенно в трансмиссиях. Циклоида в некотором смысле является более интересной и гибкой формой; однако эвольвента имеет два преимущества: ее проще изготовить и она позволяет изменять межцентровое расстояние шестерен в некотором диапазоне, не нарушая постоянства передаточного отношения. Циклоидные шестерни работают правильно только в том случае, если расстояние между центрами точно правильное. Циклоидные шестерни до сих пор широко используются в механических часах.

Перекос осей

Для непараллельных осей с непрямыми вырезами зубьев лучшим профилем зубьев является одна из нескольких форм спирально-конических зубчатых колес . К ним относятся типы Глисона (дуга окружности с непостоянной глубиной зубца), типы Эрликона и Curvex (дуга окружности с постоянной глубиной зубца), Цикло-Паллоид Клингельнберга (Эпициклоида с постоянной глубиной зубца) или Паллоид Клингельнберга. ^{[ 40 ]}

Торцы зубьев в этих типах передач представляют собой не эвольвентные цилиндры или конусы, а участки октоидальных поверхностей . ^{[ 50 ]} Для изготовления таких поверхностей зубьев может потребоваться 5-осевой фрезерный станок .

Спирально-конические шестерни имеют те же преимущества и недостатки по сравнению со своими прямыми собратьями, что и косозубые шестерни с прямозубыми, например, более низкий уровень шума и вибрации. ^{[ 40 ]} Упрощенно рассчитанные конические передачи на основе эквивалентной цилиндрической передачи нормального сечения с эвольвентной формой зуба демонстрируют отклоняющуюся форму зуба с пониженной прочностью зуба на 10-28 % без вылета и на 45 % со вылетом. ^{[ 51 ]}

Специальные зубчатые передачи

Рейка и шестерня

Рейка представляет собой зубчатый стержень или стержень, который можно рассматривать как секторную шестерню с бесконечно большим радиусом кривизны . Крутящий момент можно преобразовать в линейную силу путем зацепления рейки с круглой шестерней, называемой шестерней : шестерня вращается, а рейка движется по прямой. Такой механизм используется в рулевом управлении автомобилей для преобразования вращения рулевого колеса (тяг) слева направо, в движение рулевой тяги прикрепленных к передним колесам.

Зубчатые рейки также фигурируют в теории геометрии зубчатых колес, где, например, форма зубьев сменного набора шестерен может быть задана для рейки (бесконечный радиус), а затем из этого выводятся формы зубьев для шестерен с определенными фактическими радиусами. . Реечный тип передачи также используется в зубчатой железной дороге .

Эпициклическая зубчатая передача

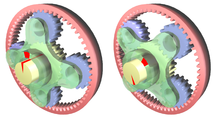
шестерни одна или несколько осей В планетарной передаче перемещается . Примерами являются солнечная и планетарная передача (см. ниже), циклоидальный привод , автоматические коробки передач и механические дифференциалы .

Солнце и планета

Солнечная и планетарная передача — это метод преобразования возвратно-поступательного движения во вращательное , который использовался в паровых двигателях . Джеймс Уатт использовал его в своих первых паровых двигателях, чтобы обойти патент на кривошип , но это также давало преимущество увеличения скорости маховика, поэтому Уатт мог использовать более легкий маховик.

На иллюстрации солнце желтое, планета красная, рычаг возвратно-поступательного движения синий, маховик зеленый, а карданный вал серый.

Некруглые шестерни

Некруглые шестерни предназначены для специальных целей. В то время как обычная передача оптимизирована для передачи крутящего момента на другой задействованный элемент с минимальным шумом и износом и максимальной эффективностью , основной целью некруглой передачи могут быть изменения передаточного числа смещения оси , колебания и многое другое. Общие области применения включают текстильные машины, потенциометры и бесступенчатые трансмиссии .

Нежесткие шестерни

Большинство зубчатых колес представляют собой идеально жесткие тела, которые передают крутящий момент и движение посредством принципа рычага и сил контакта между зубьями. А именно, крутящий момент, приложенный к одной шестерне, заставляет ее вращаться как твердое тело, так что ее зубья прижимаются к зубцам соответствующей шестерни, которая, в свою очередь, вращается как твердое тело, передавая крутящий момент на свою ось. Однако некоторые специализированные устройства избегают этой закономерности.

Гармонический механизм

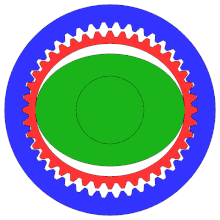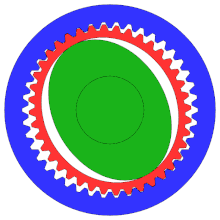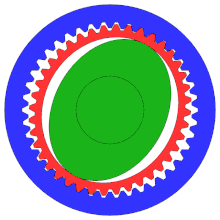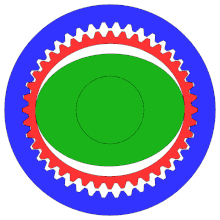
Гармоническая передача или передача волны деформации — это специализированный зубчатый механизм, часто используемый в промышленном управлении движением , робототехнике и аэрокосмической промышленности из-за его преимуществ перед традиционными системами зубчатых передач, включая отсутствие люфта, компактность и высокие передаточные числа.

Хотя на схеме не показана правильная конфигурация, это «распределительный механизм», обычно имеющий гораздо больше зубьев, чем традиционная шестерня, чтобы обеспечить более высокую степень точности.

Магнитная передача

В паре магнитных передач между двумя элементами нет контакта; вместо этого крутящий момент передается через магнитные поля. Зубцы каждой шестерни представляют собой постоянные магниты с периодическим чередованием противоположных магнитных полюсов на сопрягаемых поверхностях. Компоненты зубчатой передачи установлены с возможностью люфта, как и в других механических зубчатых передачах. Хотя они не могут оказывать такое же усилие, как традиционная шестерня, из-за ограничений по напряженности магнитного поля, такие шестерни работают без соприкосновения и поэтому невосприимчивы к износу, имеют очень низкий уровень шума, минимальные потери мощности от трения и могут скользить без повреждений, что делает их очень надежными. . ^{[ 52 ]} Их можно использовать в конфигурациях, которые невозможны для зубчатых передач, которые должны физически соприкасаться, и могут работать с неметаллическим барьером, полностью отделяющим движущую силу от нагрузки. Магнитная муфта может передавать усилие в герметичный корпус без использования радиального уплотнения вала , которое может протекать.

Номенклатура

Общий

вращения Частота , н

Измеряется во вращении с течением времени, например, в оборотах в минуту (об/мин или об/мин).

Угловая частота , ω

Измеряется в радианах/секунду . 1 об/мин = 2π рад/минута = π/30 рад/секунда.

Количество зубьев, Н

Сколько зубьев у шестерни, целое число . В случае с червями это количество запусков потоков, которые имеет червь.

Шестерня, колесо

Большая из двух взаимодействующих шестерен или отдельная шестерня.

Шестерня

Меньшая из двух взаимодействующих шестерен.

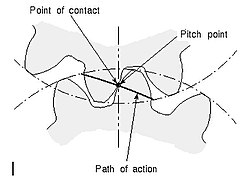
Путь контакта

Путь, по которому проходит точка контакта двух сцепившихся зубьев шестерни.

Линия действия, линия давления

Линия, вдоль которой направлена сила между двумя зацепляющимися зубьями шестерни. Он имеет то же направление, что и вектор силы. Вообще линия действия меняется от момента к моменту в период смыкания пары зубов. Однако для эвольвентных передач сила между зубьями всегда направлена по одной и той же линии, т. е. линия действия постоянна. Это означает, что для эвольвентных передач путь контакта также представляет собой прямую линию, совпадающую с линией действия, что действительно так.

Ось

Ось вращения шестерни; центральная линия вала.

Точка тангажа

Точка, в которой линия действия пересекает линию, соединяющую две оси шестерен.

Питч-круг, делительная линия

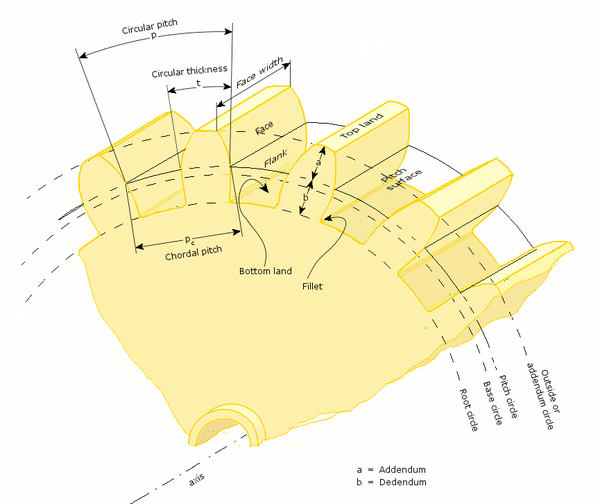
Окружность с центром и перпендикуляром к оси, проходящая через точку тангажа. Заранее определенное диаметральное положение на шестерне, где определяются толщина кругового зуба, угол давления и углы винтовой линии.

Делительный диаметр, d

Заранее определенное диаметральное положение на шестерне, где определяются толщина кругового зуба, угол давления и углы винтовой линии. Стандартный делительный диаметр является расчетным размером и не может быть измерен, но является местом, где проводятся другие измерения. Его значение основано на количестве зубьев ( N ), нормальном модуле ( m _n ; или нормальном диаметральном шаге, P _d ) и угле спирали (

\psi

):

d={\frac {Nm_{n}}{\cos \psi }}

в метрических единицах или

d={\frac {N}{P_{d}\cos \psi }}

в имперских единицах. ^{[ 53 ]}

Модуль или модуль, м

Поскольку непрактично рассчитывать круговой шаг с помощью иррациональных чисел , инженеры-механики обычно используют вместо этого масштабный коэффициент, который заменяет его обычным значением. Это известно как модуль или модуль колеса и определяется просто как:

m={\frac {p}{\pi }}

где m — модуль, а p — круговой шаг. Единицами являются модуля обычно миллиметры ; иногда Английский модуль используется с единицами измерения в дюймах . Если диаметральный шаг DP указан в английских единицах измерения,

m={\frac {25.4}{DP}}

в обычных метрических единицах.

Расстояние между двумя осями становится:

a={\frac {m}{2}}(z_{1}+z_{2})

где a — расстояние по оси, z ₁ и z ₂ — количество зубьев (зубьев) каждого из двух колес (шестерен). Эти числа (или хотя бы одно из них) часто выбирают среди простых чисел, чтобы обеспечить равномерный контакт между каждой шестерней обоих колес и тем самым избежать ненужного износа и повреждений. Равномерный износ шестерен достигается за счет того, что количество зубьев двух сцепляющихся друг с другом шестерен относительно одинаковое ; это происходит, когда наибольший общий делитель (НОД) каждого числа зубьев шестерни равен 1, например НОД(16,25)=1; если желательно передаточное число 1:1, между двумя шестернями можно вставить относительно основную передачу; при этом сохраняется соотношение 1:1, но меняется направление передачи; также может быть вставлена вторая относительно основная шестерня, чтобы восстановить исходное направление вращения, сохраняя при этом равномерный износ всех четырех шестерен. Инженеры-механики, по крайней мере в континентальной Европе, обычно используют модуль вместо кругового шага. Модуль, как и круговой шаг, можно использовать для всех типов шестерен, а не только Прямые шестерни на основе эвольвента . ^{[ 54 ]}

Диаметр рабочего шага

Диаметры определяются по количеству зубьев и межосевому расстоянию, на котором работают шестерни. ^{[ 34 ]} Пример для шестерни:

d_{w}={\frac {2a}{u+1}}={\frac {2a}{{\frac {z_{2}}{z_{1}}}+1}}.

Поверхность поля

В цилиндрических передачах цилиндр образован проекцией делительной окружности в осевом направлении. В более общем смысле, поверхность, образованная суммой всех начальных окружностей при движении вдоль оси. Для конических передач это конус.

Угол действия

Угол с вершиной в центре шестерни, одна сторона в точке первого контакта сопрягаемых зубьев, другая часть в точке, где они выходят из зацепления.

Арка действия

Сегмент основной окружности, образуемый углом действия.

Угол давления , $\theta$

Дополнение угла между направлением, в котором зубья оказывают силу друг на друга, и линией, соединяющей центры двух шестерен. У эвольвентных передач зубья всегда оказывают усилие по линии действия, которая у эвольвентных передач представляет собой прямую линию; и, таким образом, для эвольвентных передач угол давления постоянный.

Внешний диаметр, $D_{o}$

Диаметр шестерни, измеренный от вершин зубьев.

Диаметр корня

Диаметр шестерни, измеренный у основания зуба.

добавить, Чтобы

Радиальное расстояние от делительной поверхности до крайней точки зуба.

a={\frac {1}{2}}(D_{o}-D)

Чтобы дать, б

Радиальное расстояние от глубины впадины зуба до поверхности шага.

b={\frac {1}{2}}(D-{\text{root diameter}})

Вся глубина, $h_{t}$

Расстояние от верхушки зуба до корня; она равна сумме придатка плюс дедендум или рабочей глубине плюс зазор.

Распродажа

Расстояние между корневой окружностью шестерни и дополнительной окружностью сопряженной детали.

Рабочая глубина

Глубина зацепления двух передач, то есть сумма их рабочих дополнений.

Круговой шаг, п

Расстояние от одной поверхности зуба до соответствующей поверхности соседнего зуба на той же шестерне, измеренное вдоль делительной окружности.

Диаметральный шаг, DP

DP={\frac {N}{d}}={\frac {\pi }{p}}

Отношение количества зубьев к делительному диаметру. Может измеряться в зубах на дюйм или зубах на сантиметр, но обычно имеет единицы измерения на дюйм диаметра. Где модуль m находится в метрических единицах

DP={\frac {25.4}{m}}

в английских единицах

Базовый круг: В эвольвентных передачах профиль зуба создается эвольвентой базовой окружности. Радиус базовой окружности несколько меньше радиуса основной окружности.
Базовый шаг, нормальный шаг, $p_{b}$: В эвольвентных передачах расстояние от одной грани зуба до соответствующей грани соседнего зуба той же шестерни, измеренное по базовой окружности.
Помехи: Контакт между зубами, кроме предусмотренных частей их поверхностей.
Сменный комплект: Набор шестерен, каждая из которых правильно сопрягается с любой другой.

Винтовая передача

Угол спирали, $\psi$: Угол между касательной к винтовой линии и осью шестерни. В предельном случае прямозубого колеса он равен нулю, хотя его также можно рассматривать как угол гипотенузы.
Нормальный круговой шаг, $p_{n}$: Круговой шаг в плоскости, нормальной к зубьям.
Поперечный круговой шаг, п: Круговой шаг в плоскости вращения шестерни. Иногда его называют просто «круговым шагом». $p_{n}=p\cos(\psi )$

Некоторые другие параметры спирали можно просмотреть как в нормальной, так и в поперечной плоскостях. Индекс n обычно указывает на нормальное состояние.

Червячная передача

Вести: Расстояние от любой точки резьбы до соответствующей точки на следующем витке той же резьбы, измеренное параллельно оси.
Линейный шаг, п: Расстояние от любой точки резьбы до соответствующей точки соседней резьбы, измеренное параллельно оси. У однозаходного червяка шаг и линейный шаг одинаковы.
Угол подъема, $\lambda$: Угол между касательной к спирали и плоскостью, перпендикулярной оси. Обратите внимание, что для косозубых передач обычно указывается дополнение угла винтовой линии.
Диаметр шага, $d_{w}$: То же, что описано ранее в этом списке. Обратите внимание, что для червяка оно по-прежнему измеряется в плоскости, перпендикулярной оси шестерни, а не в наклонной плоскости.

Индекс w обозначает червяк, индекс g обозначает шестерню.

Контакт зуба

Линия контакта
Путь действия
Линия действия
Плоскость действия
Линии контакта (косозубая передача)
Арка действия
Продолжительность действия
Предельный диаметр
Лицо заранее
Зона действия

Контактное лицо

Любая точка, в которой два профиля зубьев касаются друг друга.

Линия контакта

Линия или кривая, вдоль которой две поверхности зуба касаются друг друга.

Путь действия

Место последовательных точек контакта между парой зубьев шестерни во время фазы зацепления. Для сопряженных зубьев шестерен путь действия проходит через точку шага. Это след поверхности действия в плоскости вращения.

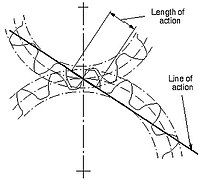
Линия действия

Путь действия эвольвентных передач. Это прямая линия, проходящая через точку тангажа и касающаяся обеих базовых окружностей.

Поверхность действия

Воображаемая поверхность, на которой происходит контакт между двумя контактирующими поверхностями зубьев. Это сумма путей действия во всех отделах сцепляющихся зубьев.

Плоскость действия

Рабочая поверхность эвольвентных параллельных передач с прямозубыми или косозубыми зубьями. Он касается основных цилиндров.

Зона действия (зона контакта)

Для эвольвентных параллельных зубчатых колес с прямозубыми или косозубыми зубьями - это прямоугольная площадь в плоскости действия, ограниченная длиной действия и эффективной шириной поверхности .

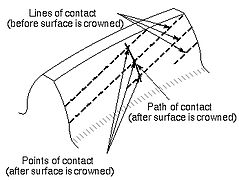
Путь контакта

Кривая на любой поверхности зуба, вдоль которой происходит теоретический одноточечный контакт во время зацепления шестерен с корончатыми поверхностями зубьев или шестерен, которые обычно входят в зацепление только с одноточечным контактом.

Продолжительность действия

Расстояние на линии действия, на которое перемещается точка контакта при действии профиля зуба.

Дуга действия, Q _t

Дуга делительной окружности, по которой движется профиль зуба от начала до конца контакта с сопрягаемым профилем.

Дуга подхода, Q _a

Дуга делительной окружности, по которой профиль зуба движется от начала контакта до тех пор, пока точка контакта не достигнет точки делителя.

Дуга впадины, Q _r

Дуга делительной окружности, по которой профиль зуба движется от контакта в делительной точке до момента прекращения контакта.

Коэффициент контакта, м _c , ε

Число угловых шагов, на которые поворачивается поверхность зуба от начала до конца контакта. Упрощенно его можно определить как меру среднего числа зубьев, находящихся в контакте за период, в течение которого зуб входит и выходит из контакта с сопряженной шестерней.

Коэффициент поперечного контакта, м _п , ε _α

Коэффициент контакта в поперечной плоскости. Это отношение угла действия к угловому шагу. Для эвольвентных передач его наиболее непосредственно можно получить как отношение длины действия к базовому шагу.

Коэффициент контакта грани, м _F , e _b

Коэффициент контакта в осевой плоскости или отношение ширины торца к осевому шагу. Для конических и гипоидных передач это отношение выдвижения торца к круговому шагу.

Общий коэффициент контакта, m _t , ε _γ

Сумма коэффициента поперечного контакта и коэффициента контакта торца.

\epsilon _{\gamma }=\epsilon _{\alpha }+\epsilon _{\beta }

m_{\rm {t}}=m_{\rm {p}}+m_{\rm {F}}

Модифицированный коэффициент контакта, м _о

Для конических передач – квадратный корень из суммы квадратов передаточных чисел поперечного и торцового контакта.

m_{\rm {o}}={\sqrt {m_{\rm {p}}^{2}+m_{\rm {F}}^{2}}}

Предельный диаметр: Диаметр шестерни, при котором линия действия пересекает максимальную (или минимальную для внутренней шестерни) дополнительную окружность сопряженной шестерни. Это также называется началом активного профиля, началом контакта, окончанием контакта или концом активного профиля.
Запуск активного профиля (SAP): Пересечение предельного диаметра и эвольвентного профиля.
Лицо заранее: Расстояние на делительной окружности, на которое винтовой или спиральный зуб перемещается от положения, в котором начинается контакт на одном конце следа зуба на делительной поверхности, до положения, в котором контакт прекращается на другом конце.

Толщина зуба

Толщина зуба
Отношения толщины
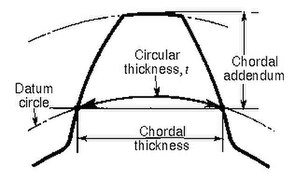
Толщина хорды
Измерение толщины зуба на штифтах
Измерение диапазона
Длинные и короткие придаточные зубы

Толщина круга: Длина дуги между двумя сторонами зуба шестерни на указанной базовой окружности .
Поперечная круговая толщина: Толщина круга в поперечной плоскости.
Нормальная круглая толщина: Толщина круга в нормальной плоскости. В косозубой передаче ее можно рассматривать как длину дуги нормальной винтовой линии.
Осевая толщина: В косозубых передачах и червяках толщина зуба в осевом сечении при стандартном делительном диаметре.
Базовая круглая толщина: В эвольвентных зубьях — длина дуги базовой окружности между двумя эвольвентными кривыми, образующими профиль зуба.
Нормальная толщина хорд: Длина хорды, образующей дугу окружности толщиной в плоскости, нормальной к основной спирали. Можно выбрать любой удобный измерительный диаметр, не обязательно стандартный делительный диаметр.
Хордальное дополнение (высота хорды): Высота от вершины зуба до хорды, образующей дугу толщины окружности. Можно выбрать любой удобный измерительный диаметр, не обязательно стандартный делительный диаметр.
Сдвиг профиля: Смещение базовой линии стойки от эталонного цилиндра, сделанное безразмерным путем деления на нормальный модуль. Он используется для указания толщины зуба, часто для нулевого люфта.
Смена стойки: Смещение базовой линии инструмента от эталонного цилиндра, сделанное безразмерным путем деления на нормальный модуль. Он используется для указания толщины зуба.
Измерение через штифты: Измерение расстояния между штифтом, расположенным в пространстве зуба, и базовой поверхностью. Базовой поверхностью может быть базовая ось зубчатого колеса, базовая поверхность или один или два штифта, расположенных в пространстве зубьев или пространствах напротив первого. Это измерение используется для определения толщины зуба.
Измерение диапазона: Измерение расстояния поперек нескольких зубов в нормальной плоскости. Пока измерительное устройство имеет параллельные измерительные поверхности, которые контактируют с неизмененной частью эвольвенты, измерение производится вдоль линии, касательной к базовому цилиндру. Используется для определения толщины зуба.
Модифицированные дополнительные зубы: Зубья шестерен включения, одна или обе из которых имеют нестандартную приставку.
Зубы на всю глубину: Зубья, у которых рабочая глубина равна 2000, разделенному на нормальный диаметральный шаг.
Короткие зубы: Зубья, у которых рабочая глубина меньше 2000, разделенных на нормальный диаметральный шаг.
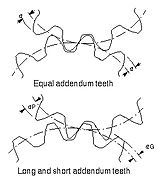
Равные дополнительные зубы: Зубья, у которых две зацепляющие шестерни имеют одинаковые придатки.
Длинные и короткие придаточные зубы: Зубья, у которых сростки двух зацепляющих шестерен неравны.

Подрез: Подрез — это состояние сформированных зубьев шестерни, когда любая часть кривой скругления лежит внутри линии, проведенной по касательной к рабочему профилю в точке его соединения с скруглением. Подрез может быть введен намеренно для облегчения чистовых операций. При подрезе кривая скругления пересекает рабочий профиль. Без подреза кривая скругления и рабочий профиль имеют общую касательную.
Корневое филе: или кривая скругления, вогнутая часть профиля зуба, где он соединяется с нижней частью зубного пространства. ²

Подача

Шаг — это расстояние между точкой на одном зубе и соответствующей точкой на соседнем зубе. ^{[ 34 ]} Это размер, измеренный вдоль линии или кривой в поперечном, нормальном или осевом направлениях. Использование одного слова «шаг» без уточнений может быть неоднозначным, и по этой причине предпочтительно использовать конкретные обозначения, такие как поперечный круговой шаг, нормальный базовый шаг, осевой шаг.

Подача
Шаг зубьев
Отношения базовой подачи
Основные передачи

Круговой шаг, п

Расстояние по дуге вдоль заданной делительной окружности или делительной линии между соответствующими профилями соседних зубьев.

Поперечный круговой шаг, p _t

Круговой шаг в поперечной плоскости.

Нормальный круговой шаг, p _n , p _e

Круговой шаг в нормальной плоскости, а также длина дуги по спирали с нормальным шагом между винтовыми зубьями или резьбами.

Осевой шаг, п _х

Линейный шаг в осевой плоскости и на поверхности шага. В косозубых передачах и червяках осевой шаг имеет одинаковое значение на всех диаметрах. В зубчатых передачах других типов осевой шаг может ограничиваться поверхностью шага и может иметь круговое измерение. Термин «осевой шаг» предпочтительнее термина «линейный шаг». Осевой шаг винтового червяка и круговой шаг его червячной передачи одинаковы.

Нормальный базовый шаг, p _N , p _bn

Эвольвентная косозубая передача представляет собой базовый шаг в нормальной плоскости. Это нормальное расстояние между параллельными винтовыми эвольвентными поверхностями в плоскости действия в нормальной плоскости или длина дуги нормальной базовой спирали. Это постоянное расстояние в любой косозубой эвольвентной передаче.

Поперечный шаг основания, p _b , p _bt

В эвольвентной передаче шаг находится на базовой окружности или по линии действия. Соответствующие стороны зубьев эвольвентного колеса представляют собой параллельные кривые, а базовый шаг представляет собой постоянное и фундаментальное расстояние между ними по общей нормали в поперечной плоскости.

Диаметральный шаг (поперечный), Р _д

Отношение количества зубьев к стандартному делительному диаметру в дюймах.

P_{\rm {d}}={\frac {N}{d}}={\frac {25.4}{m}}={\frac {\pi }{p}}

Нормальный диаметральный шаг, P _nd

Значение диаметрального шага в нормальной плоскости косозубого колеса или червяка.

P_{\rm {nd}}={\frac {P_{\rm {d}}}{\cos \psi }}

Угловой шаг, θ _N , τ

Угол, образуемый круглым шагом, обычно выражается в радианах.

\tau ={\frac {360}{z}}

градусов или

{\frac {2\pi }{z}}

радианы

Люфт

Люфт – это ошибка в движении, возникающая при изменении направления шестерен. Это существует потому, что между задней поверхностью ведущего зуба и передней поверхностью зуба позади него на ведомой шестерне всегда существует некоторый зазор, и этот зазор должен быть закрыт, прежде чем сила сможет быть передана в новом направлении. Термин «обратная реакция» также может использоваться для обозначения размера разрыва, а не только явления, которое он вызывает; таким образом, можно говорить о паре шестерен, имеющей, например, «люфт 0,1 мм». Пара шестерен может быть спроектирована так, чтобы иметь нулевой люфт, но это предполагает совершенство производства, одинаковые характеристики теплового расширения во всей системе и отсутствие смазки. Поэтому зубчатые пары спроектированы так, чтобы иметь некоторый люфт. Обычно это достигается за счет уменьшения толщины зубьев каждой шестерни на половину желаемого зазора. Однако в случае большой шестерни и маленькой шестерни люфт обычно полностью устраняется, и шестерня получает полноразмерные зубья. Люфт также можно обеспечить, раздвинув шестерни дальше друг от друга. Обратная реакция зубчатая передача равна сумме люфта каждой пары шестерен, поэтому в длинных передачах люфт может стать проблемой.

В ситуациях, требующих точности, таких как контрольно-измерительные приборы и контроль, люфт можно минимизировать с помощью одного из нескольких методов. Например, шестерню можно разделить в плоскости, перпендикулярной оси, при этом одна половина будет прикреплена к валу обычным способом, а другая половина будет размещена рядом с ним, свободно вращаясь вокруг вала, но с пружинами между двумя половинами, обеспечивающими относительный крутящий момент между ними, так что фактически получается одна шестерня с расширяющимися зубьями. Другой метод заключается в сужении зубьев в осевом направлении и обеспечении скольжения шестерни в осевом направлении для устранения провисания.

Стандартные площадки и модульная система

Хотя шестерни могут быть изготовлены с любым шагом, для удобства и взаимозаменяемости часто используются стандартные шаги. Шаг — это свойство, связанное с линейными размерами , поэтому оно различается в зависимости от того, указаны ли стандартные значения в британских (дюймах) или метрических системах. Используя дюймовые измерения, выбираются стандартные значения диаметрального шага с единицами измерения «на дюйм»; Диаметральный шаг — это количество зубьев на шестерне с диаметром шага в один дюйм. Общие стандартные значения для прямозубых шестерен: 3, 4, 5, 6, 8, 10, 12, 16, 20, 24, 32, 48, 64, 72, 80, 96, 100, 120 и 200. ^{[ 55 ]} Определенные стандартные шаги, такие как 1/10 и 1/20 дюйма, которые соответствуют линейной стойке, на самом деле представляют собой (линейные) значения кругового шага с единицами измерения «дюймы». ^{[ 55 ]}

Когда размеры шестерни указаны в метрической системе, характеристика шага обычно выражается в модуле или модуле , который фактически представляет собой измерение длины по делительному диаметру . Под модулем понимают средний диаметр в миллиметрах, разделенный на количество зубьев. Если модуль основан на дюймовых измерениях, его называют английским модулем, чтобы избежать путаницы с метрическим модулем. Модуль представляет собой прямой размер («миллиметры на зуб»), в отличие от диаметрального шага, который является обратным размером («зубьев на дюйм»). Таким образом, если делительный диаметр шестерни 40 мм и количество зубьев 20, то модуль равен 2, что означает, что на каждый зуб приходится 2 мм делительного диаметра. ^{[ 56 ]} Предпочтительные значения стандартных модулей: 0,1, 0,2, 0,3, 0,4, 0,5, 0,6, 0,8, 1,0, 1,25, 1,5, 2,0, 2,5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40 и 50. ^{[ 57 ]}

Модель шестерни в современной физике

Современная физика по-разному восприняла модель шестерни. В девятнадцатом веке Джеймс Клерк Максвелл разработал модель электромагнетизма , в которой силовые линии магнитного поля представляют собой вращающиеся трубки несжимаемой жидкости. Максвелл использовал зубчатое колесо и назвал его «холостым колесом», чтобы объяснить электрический ток как вращение частиц в направлениях, противоположных направлению вращающихся силовых линий. ^{[ 58 ]}

Совсем недавно квантовая физика использовала в своей модели «квантовые шестерни». Группа шестерен может служить моделью для нескольких различных систем, например, искусственно созданного наномеханического устройства или группы кольцевых молекул. ^{[ 59 ]}

сравнивает Трехволновая гипотеза корпускулярно -волновой дуализм с конической передачей. ^{[ 60 ]}

Механизм зубчатой передачи в мире природы

Зубчатый механизм раньше считался исключительно искусственным, но уже в 1957 году шестерни были обнаружены в задних лапах различных видов цикадок. ^{[ 61 ]} а ученые из Кембриджского университета в 2013 году охарактеризовали их функциональное значение, выполнив высокоскоростную фотографию нимф Issus coleoptratus в Кембриджском университете. ^{[ 62 ]}^{[ 63 ]} Эти шестерни встречаются только у нимф всех цикадок и теряются во время финальной линьки на взрослую стадию. ^{[ 64 ]} У I. coleoptratus каждая нога имеет полосу зубьев шириной 400 микрометров, радиус шага 200 микрометров, с 10–12 полностью переплетенными прямозубыми зубьями, включая скругленные кривые у основания каждого зуба для уменьшения риска сдвига. ^{[ 65 ]} Сустав вращается, как механические шестерни, и синхронизирует задние ноги Иссуса , когда он прыгает с точностью до 30 микросекунд, предотвращая вращение рыскания. ^{[ 66 ]}^{[ 67 ]}^{[ 62 ]} Шестерни не всегда подключаются. По одному расположено на каждой задней ноге молодого насекомого, и когда оно готовится к прыжку, два набора зубов смыкаются вместе. В результате ноги двигаются почти идеально синхронно, давая насекомому больше силы, поскольку шестерни вращаются до точки остановки, а затем разблокируются. ^{[ 66 ]}

См. также

Ссылки

^ Определение слова «снаряжение» в онлайн- словаре Merriam-Webster , смысл (6a). Доступ осуществлен 20 сентября 2018 г.
^ Определение слова «снаряжение» в Оксфордском онлайн-словаре для учащихся . Доступ осуществлен 27 июля 2024 г.
^ Определение слова «шестеренка» в онлайн- словаре английского языка Коллинза . Доступ осуществлен 27 июля 2024 г.
^ Определение слова «шестерня» в онлайн-словаре Merriam-Webster. Доступ осуществлен 20 сентября 2018 г.
^ Определение слова «шестерня» в Оксфордском онлайн-словаре для учащихся . Доступ осуществлен 27 июля 2024 г.
^ Jump up to: ^а ^б Определение слова «винтик» в Оксфордском онлайн-словаре для учащихся . Доступ осуществлен 29 июля 2024 г.
^ Определение слова «винтик» в онлайн- словаре Merriam-Webster . Доступ осуществлен 29 июля 2024 г.
^ Jump up to: ^а ^б Определение слова «винтик» в онлайн- кембриджском словаре Plus . Доступ осуществлен 29 июля 2024 г.
^ Определение слова «винтик» в онлайн- словаре английского языка Коллинза . Доступ осуществлен 29 июля 2024 г.
^ Шуайлонг Чжан, Мохамед Эльсаед, Ран Пэн, Юцзе Чен (2021): «Реконфигурируемые многокомпонентные микромашины, приводимые в движение оптоэлектронными пинцетами». Nature Communications , том 12, выпуск 1. два : 10.1038/s41467-021-25582-8
^ Мэтью Джастер (2013): [ https://www.geartechnology.com/ext/resources/issues/0313x/worlds_largest_gears.pdf «МОЕ МЕХАНИЗМ больше, чем ВАШЕ МЕХАНИЗМ: Индустрия борется за звание крупнейшего в мире оборудования»]. Интернет-статья из Gear Technology журнала . Архивировано 30 июля 2024 г.
^ «Рычаги - Моменты, рычаги и шестерни - AQA - Версия GCSE Physics (Single Science) - AQA - BBC Bitesize» . BBC.co.uk. 1 января 1970 года . Проверено 16 марта 2022 г.
^ «Основы передачи» . Как все работает . 27 апреля 2005 г.
^ Дерек Дж. де Солла Прайс , О происхождении часового механизма, вечных двигателей и компаса , стр.84
^ «Шестерни от Архимеда, Герона и Дионисия» . www.hellenicaworld.com . Проверено 21 ноября 2023 г.
^ Нортон 2004 , с. 462
^ Льюис, MJT (1993). «Передача в древнем мире». Стараться . 17 (3): 110–115. дои : 10.1016/0160-9327(93)90099-О .
^ «Проект исследования антикитерского механизма: почему это так важно?» . Архивировано из оригинала 4 мая 2012 года . Проверено 10 января 2011 г. Считается, что этот механизм возник между 150 и 100 годами до нашей эры.
^ Оуэн Джарус (14 апреля 2022 г.). «Первый в мире компьютер, Антикитерский механизм, «запустился» в 178 году до нашей эры, утверждают ученые» . www.livscience.com . Проверено 5 июня 2022 г.
^ Фрит, Тони. «Древнегреческая астрономическая вычислительная машина раскрывает новые тайны» . Научный американец . Проверено 5 июня 2022 г.
^ Джозеф Нидэм (1986). Наука и цивилизация в Китае: Том 4, Часть 2 , стр. 298. Тайбэй: Caves Books, Ltd.
^ «вертикальный циферблат | Британский музей» . Британский музей . Проверено 5 июня 2022 г.
^ «Портативный византийский календарь солнечных часов: второй древнейший из существующих механизмов с приводом» . www.thearchaeological.org . Проверено 5 июня 2022 г.
^ «Астролябия Мухаммада ибн Аби Бакра аль-Исфахани» .
^ Ирфан Хабиб , Экономическая история средневековой Индии, 1200-1500 , стр. 53 , Pearson Education
^ «Астрариум Джованни Донди, 1364 год | кабинет» . www.cabinet.ox.ac.uk . Проверено 5 июня 2022 г.
^ «шестеренка (сущ.)» . Этимонлин . Проверено 13 февраля 2020 г. .
^ «Этимология 1: Зубец (существительное)» . Викисловарь . Проверено 29 июля 2019 г.
^ "винтик (существительное) " Этимология Проверено 13 февраля 2020 г. .
^ Грант, Джордж Б. (1893). Трактат о зубчатых колесах (6-е, илл. изд.). Лексингтон, Массачусетс; Филадельфия, Пенсильвания: Джордж Б. Грант. п. 21 .
^ Смит, Зан (2000): «Пластиковые шестерни становятся более надежными, если при проектировании инженеры учитывают свойства материала и производственные процессы». , Motion System Design , архивировано из оригинала 14 июля 2011 года , получено 7 января 2011 года .
^ Радзевич, Стивен П. (2012). Справочник Дадли по практическому проектированию и производству зубчатого оборудования (PDF) (2-е изд.). Бока-Ратон, Флорида: CRC Press, издательство Taylor & Francisco Group. стр. 691, 702.
^ Фред Эберле (август 2014 г.). «Материалы имеют значение» . Решения для передач : 22.
^ Jump up to: ^а ^б ^с ^д ^и Американская ассоциация производителей зубчатого оборудования ; Американский национальный институт стандартов, Номенклатура зубчатых передач, Определения терминов с символами (издание ANSI/AGMA 1012-G05), Американская ассоциация производителей зубчатых передач
^ Кэнфилд, Стивен (1997), «Типы передач» , Динамика машин , Технологический университет Теннесси, факультет машиностроения, ME 362 конспекта лекций, заархивировано из оригинала 29 августа 2008 г.
^ Гильберт, Дэвид ; Кон-Воссен, Стефан (1952), Геометрия и воображение (2-е изд.), Нью-Йорк: Челси, с. 287, ISBN 978-0-8284-1087-8 .
^ Jump up to: ^а ^б МакГроу-Хилл 2007 , с. 743.
^ «Как работают шестерни» . Howstuffworks.com . 16 ноября 2000 г. Проверено 20 сентября 2018 г.
^ Справочник машиниста . Нью-Йорк: Промышленная пресса. 2012. С. 2125 . ISBN 978-0-8311-2900-2 .
^ Jump up to: ^а ^б ^с МакГроу-Хилл 2007 , с. 742.
^ Хурми Р.С., Теория машин , С.ЧАНД
^ Шунк, Ричард, «Минимизация шума коробки передач внутри и снаружи коробки» , Motion System Design . ^{[ постоянная мертвая ссылка ]}
^ Валланс и Даути 1964 , с. 281
^ Jump up to: ^а ^б Косозубые шестерни , заархивировано из оригинала 26 июня 2009 года , получено 15 июня 2009 года .
^ Валланс и Даути 1964 , с. 287.
^ Vallance & Doughtie 1964 , стр. 280, 296.
^ Валланс и Даути 1964 , с. 290.
^ МакГроу-Хилл 2007 , с. 744
^ Фрит, Тони; Джонс, Александр (февраль 2012 г.). «Космос в Антикитерском механизме» . Документы ISAW (4). Институт изучения древнего мира – через Нью-Йоркский университет .
^ Джорджио Фильолини, Хорхе Анхелес (2005): «Алгоритмы для создания эвольвентных и октоидальных конических шестерен». Журнал механического проектирования , том 127, выпуск 4. дои : 10.1115/1.1900147
^ Дисс. Хюнеке, Технический университет Дрездена.
^ Кравченко А.И., Бовда А.М. Механизм с магнитной парой. Пэт. Украины № 56700 – Бюл. № 2, 2011 г. – F16H 49/00.
^ ISO / DIS 21771: 2007: «Шестерни — цилиндрические эвольвентные шестерни и пары шестерен — концепции и геометрия», Международная организация по стандартизации , (2007).
^ Гуннар Дальвиг (1982), «Элементы конструкции и машиностроение», Konstruktionselement och машиностроение (на шведском языке), 7, ISBN 978-9140115546
^ Jump up to: ^а ^б «Справочное руководство по оборудованию WM Berg» (PDF) . Архивировано из оригинала (PDF) 21 апреля 2015 года.
^ Оберг, Э.; Джонс, Флорида; Хортон, Х.Л.; Риффелл, Х.Х. (2000), Справочник по машинному оборудованию (26-е изд.), Industrial Press, стр. 2649, ISBN 978-0-8311-2666-7 .
^ «Элементы технологии метрических передач» (PDF) .
^ Сигел, Дэниел М. (1991). Инновации в электромагнитной теории Максвелла: молекулярные вихри, ток смещения и свет . Издательство Чикагского университета. ISBN 978-0521353656 .
^ Маккиннон, Ангус (2002). «Квантовые механизмы: простая механическая система в квантовом режиме». Нанотехнологии . 13 (5): 678–681. arXiv : cond-mat/0205647 . Бибкод : 2002Nanot..13..678M . дои : 10.1088/0957-4484/13/5/328 . S2CID 14994774 .
^ Сандук, Мичиган (2007). «Подразумевает ли гипотеза трех волн скрытую структуру?» (PDF) . Апейрон . 14 (2): 113–125. Бибкод : 2007Apei...14..113S .
^ Сандер, К. (1957), «Строение и функции прыжкового аппарата Pyrilla perpusilla WALKER (Homoptera - Fulgoridae)», Zool. Иб. Йена (Анат.) (на немецком языке), 75 : 383–388.
^ Jump up to: ^а ^б Берроуз, Малькольм; Саттон, Грегори (13 сентября 2013 г.). «Взаимодействующие шестерни синхронизируют движения ног прыгающего насекомого» . Наука . 341 (6151): 1254–1256. Бибкод : 2013Sci...341.1254B . дои : 10.1126/science.1240284 . hdl : 1983/69cf1502-217a-4dca-a0d3-f8b247794e92 . ПМИД 24031019 . S2CID 24640726 .
^ Херкевиц, Уильям (12 сентября 2013 г.), «Первая шестерня, обнаруженная в природе» , «Популярная механика».
^ Ли, Джейн Дж. (12 сентября 2013 г.), «Насекомые используют шестерни на задних лапах, чтобы прыгать» , National Geographic , заархивировано из оригинала 13 сентября 2013 г.
^ Стромберг, Джозеф (12 сентября 2013 г.), «У этого насекомого единственные механические механизмы, когда-либо найденные в природе» , журнал Smithsonian Magazine , получено 18 ноября 2020 г.
^ Jump up to: ^а ^б Робертсон, Ади (12 сентября 2013 г.). «Первые в природе шестеренки обнаружены на ногах насекомых» . Грань . Проверено 14 сентября 2013 г.
^ Функционирующие «механические шестерни» впервые замечены в природе , PHYS.ORG, Кембриджский университет

Библиография

McGraw-Hill (2007), Энциклопедия науки и технологий McGraw-Hill (10-е изд.), McGraw-Hill Professional, ISBN 978-0-07-144143-8 .
Нортон, Роберт Л. (2004), Проектирование машин (3-е изд.), McGraw-Hill Professional, ISBN 978-0-07-121496-4 .
Валланс, Алекс; Даути, Вентон Леви (1964), Проектирование элементов машины (4-е изд.), McGraw-Hill.
Industrial Press (2012), Справочник машинного оборудования (29-е изд.), ISBN 978-0-8311-2900-2
Engineers Edge, проектирование зубчатых передач и инженерные данные .

Дальнейшее чтение

Американская ассоциация производителей зубчатого оборудования ; Американский национальный институт стандартов (2005 г.), Номенклатура зубчатых передач: определения терминов с символами (изд. ANSI/AGMA 1012-F90), Американская ассоциация производителей зубчатых передач, ISBN 978-1-55589-846-5 .
Бэкингем, Эрл (1949), Аналитическая механика зубчатых передач , McGraw-Hill Book Co..
Кой, Джон Дж.; Таунсенд, Деннис П.; Зарецкий, Эрвин В. (1985), Гиринг (PDF) , НАСА Отдел научно-технической информации , NASA-RP-1152; Технический отчет AVSCOM 84-C-15.
Кравченко А.И., Бовда А.М. Передача с магнитной парой. Пэт. Украины № 56700 – Бюл. № 2, 2011 г. – F16H 49/00.
Склейтер, Нил. (2011). «Передачи: устройства, приводы и механизмы». Справочник по механизмам и механическим устройствам. 5-е изд. Нью-Йорк: МакГроу Хилл. стр. 131–174. ISBN 9780071704427 . Чертежи и конструкции различных зубчатых передач.
«Колеса, которые не могут скользить». Popular Science , февраль 1945 г., стр. 120–125.

Внешние ссылки

Гиарариум. Музей шестерен и зубчатых колес - старинные и старинные шестерни, звездочки, трещотки и другие предметы, связанные с шестернями.
Цифровая библиотека кинематических моделей для проектирования (KMODDL) - фильмы и фотографии сотен рабочих моделей в Корнельском университете.
Краткий исторический отчет о применении аналитической геометрии к форме зубьев шестерен.
Математический учебник по зубчатым передачам (относящийся к робототехнике)
Американская ассоциация производителей зубчатого оборудования
Gear Technology, журнал по производству зубчатых передач

[1] Определение слова «снаряжение» в онлайн- словаре Merriam-Webster , смысл (6a). Доступ осуществлен 20 сентября 2018 г.

[2] Определение слова «снаряжение» в Оксфордском онлайн-словаре для учащихся . Доступ осуществлен 27 июля 2024 г.

[3] Определение слова «шестеренка» в онлайн- словаре английского языка Коллинза . Доступ осуществлен 27 июля 2024 г.

[4] Определение слова «шестерня» в онлайн-словаре Merriam-Webster. Доступ осуществлен 20 сентября 2018 г.

[5] Определение слова «шестерня» в Оксфордском онлайн-словаре для учащихся . Доступ осуществлен 27 июля 2024 г.

[oxfoCOG-6] Jump up to: ^а ^б Определение слова «винтик» в Оксфордском онлайн-словаре для учащихся . Доступ осуществлен 29 июля 2024 г.

[merrCOG-7] Определение слова «винтик» в онлайн- словаре Merriam-Webster . Доступ осуществлен 29 июля 2024 г.

[cambCOG-8] Jump up to: ^а ^б Определение слова «винтик» в онлайн- кембриджском словаре Plus . Доступ осуществлен 29 июля 2024 г.

[collGOG-9] Определение слова «винтик» в онлайн- словаре английского языка Коллинза . Доступ осуществлен 29 июля 2024 г.

[zhan2021-10] Шуайлонг Чжан, Мохамед Эльсаед, Ран Пэн, Юцзе Чен (2021): «Реконфигурируемые многокомпонентные микромашины, приводимые в движение оптоэлектронными пинцетами». Nature Communications , том 12, выпуск 1. два : 10.1038/s41467-021-25582-8

[jast2013-11] Мэтью Джастер (2013): [ https://www.geartechnology.com/ext/resources/issues/0313x/worlds_largest_gears.pdf «МОЕ МЕХАНИЗМ больше, чем ВАШЕ МЕХАНИЗМ: Индустрия борется за звание крупнейшего в мире оборудования»]. Интернет-статья из Gear Technology журнала . Архивировано 30 июля 2024 г.

[12] «Рычаги - Моменты, рычаги и шестерни - AQA - Версия GCSE Physics (Single Science) - AQA - BBC Bitesize» . BBC.co.uk. 1 января 1970 года . Проверено 16 марта 2022 г.

[13] «Основы передачи» . Как все работает . 27 апреля 2005 г.

[Derek-14] Дерек Дж. де Солла Прайс , О происхождении часового механизма, вечных двигателей и компаса , стр.84

[15] «Шестерни от Архимеда, Герона и Дионисия» . www.hellenicaworld.com . Проверено 21 ноября 2023 г.

[16] Нортон 2004 , с. 462

[17] Льюис, MJT (1993). «Передача в древнем мире». Стараться . 17 (3): 110–115. дои : 10.1016/0160-9327(93)90099-О .

[18] «Проект исследования антикитерского механизма: почему это так важно?» . Архивировано из оригинала 4 мая 2012 года . Проверено 10 января 2011 г. Считается, что этот механизм возник между 150 и 100 годами до нашей эры.

[19] Оуэн Джарус (14 апреля 2022 г.). «Первый в мире компьютер, Антикитерский механизм, «запустился» в 178 году до нашей эры, утверждают ученые» . www.livscience.com . Проверено 5 июня 2022 г.

[20] Фрит, Тони. «Древнегреческая астрономическая вычислительная машина раскрывает новые тайны» . Научный американец . Проверено 5 июня 2022 г.

[21] Джозеф Нидэм (1986). Наука и цивилизация в Китае: Том 4, Часть 2 , стр. 298. Тайбэй: Caves Books, Ltd.

[vertical_dial_{{!}}_British_Museum-22] «вертикальный циферблат | Британский музей» . Британский музей . Проверено 5 июня 2022 г.

[23] «Портативный византийский календарь солнечных часов: второй древнейший из существующих механизмов с приводом» . www.thearchaeological.org . Проверено 5 июня 2022 г.

[24] «Астролябия Мухаммада ибн Аби Бакра аль-Исфахани» .

[india-25] Ирфан Хабиб , Экономическая история средневековой Индии, 1200-1500 , стр. 53 , Pearson Education

[26] «Астрариум Джованни Донди, 1364 год | кабинет» . www.cabinet.ox.ac.uk . Проверено 5 июня 2022 г.

[27] «шестеренка (сущ.)» . Этимонлин . Проверено 13 февраля 2020 г. .

[28] «Этимология 1: Зубец (существительное)» . Викисловарь . Проверено 29 июля 2019 г.

[29] "винтик (существительное) " Этимология Проверено 13 февраля 2020 г. .

[30] Грант, Джордж Б. (1893). Трактат о зубчатых колесах (6-е, илл. изд.). Лексингтон, Массачусетс; Филадельфия, Пенсильвания: Джордж Б. Грант. п. 21 .

[31] Смит, Зан (2000): «Пластиковые шестерни становятся более надежными, если при проектировании инженеры учитывают свойства материала и производственные процессы». , Motion System Design , архивировано из оригинала 14 июля 2011 года , получено 7 января 2011 года .

[32] Радзевич, Стивен П. (2012). Справочник Дадли по практическому проектированию и производству зубчатого оборудования (PDF) (2-е изд.). Бока-Ратон, Флорида: CRC Press, издательство Taylor & Francisco Group. стр. 691, 702.

[33] Фред Эберле (август 2014 г.). «Материалы имеют значение» . Решения для передач : 22.

[ansiagma-34] Jump up to: ^а ^б ^с ^д ^и Американская ассоциация производителей зубчатого оборудования ; Американский национальный институт стандартов, Номенклатура зубчатых передач, Определения терминов с символами (издание ANSI/AGMA 1012-G05), Американская ассоциация производителей зубчатых передач

[35] Кэнфилд, Стивен (1997), «Типы передач» , Динамика машин , Технологический университет Теннесси, факультет машиностроения, ME 362 конспекта лекций, заархивировано из оригинала 29 августа 2008 г.

[36] Гильберт, Дэвид ; Кон-Воссен, Стефан (1952), Геометрия и воображение (2-е изд.), Нью-Йорк: Челси, с. 287, ISBN 978-0-8284-1087-8 .

[hypoidgears-37] Jump up to: ^а ^б МакГроу-Хилл 2007 , с. 743.

[38] «Как работают шестерни» . Howstuffworks.com . 16 ноября 2000 г. Проверено 20 сентября 2018 г.

[39] Справочник машиниста . Нью-Йорк: Промышленная пресса. 2012. С. 2125 . ISBN 978-0-8311-2900-2 .

[straightbevel-40] Jump up to: ^а ^б ^с МакГроу-Хилл 2007 , с. 742.

[41] Хурми Р.С., Теория машин , С.ЧАНД

[42] Шунк, Ричард, «Минимизация шума коробки передач внутри и снаружи коробки» , Motion System Design . ^{[ постоянная мертвая ссылка ]}

[pitchlinespeed-43] Валланс и Даути 1964 , с. 281

[roymech-44] Jump up to: ^а ^б Косозубые шестерни , заархивировано из оригинала 26 июня 2009 года , получено 15 июня 2009 года .

[wormgears1-45] Валланс и Даути 1964 , с. 287.

[wormgears2-46] Vallance & Doughtie 1964 , стр. 280, 296.

[wormgears4-47] Валланс и Даути 1964 , с. 290.

[wormgears5-48] МакГроу-Хилл 2007 , с. 744

[free2012-49] Фрит, Тони; Джонс, Александр (февраль 2012 г.). «Космос в Антикитерском механизме» . Документы ISAW (4). Институт изучения древнего мира – через Нью-Йоркский университет .

[figl2005-50] Джорджио Фильолини, Хорхе Анхелес (2005): «Алгоритмы для создания эвольвентных и октоидальных конических шестерен». Журнал механического проектирования , том 127, выпуск 4. дои : 10.1115/1.1900147

[51] Дисс. Хюнеке, Технический университет Дрездена.

[52] Кравченко А.И., Бовда А.М. Механизм с магнитной парой. Пэт. Украины № 56700 – Бюл. № 2, 2011 г. – F16H 49/00.

[Standardization,_2007-53] ISO / DIS 21771: 2007: «Шестерни — цилиндрические эвольвентные шестерни и пары шестерен — концепции и геометрия», Международная организация по стандартизации , (2007).

[54] Гуннар Дальвиг (1982), «Элементы конструкции и машиностроение», Konstruktionselement och машиностроение (на шведском языке), 7, ISBN 978-9140115546

[Berg-55] Jump up to: ^а ^б «Справочное руководство по оборудованию WM Berg» (PDF) . Архивировано из оригинала (PDF) 21 апреля 2015 года.

[MH26-56] Оберг, Э.; Джонс, Флорида; Хортон, Х.Л.; Риффелл, Х.Х. (2000), Справочник по машинному оборудованию (26-е изд.), Industrial Press, стр. 2649, ISBN 978-0-8311-2666-7 .

[57] «Элементы технологии метрических передач» (PDF) .

[58] Сигел, Дэниел М. (1991). Инновации в электромагнитной теории Максвелла: молекулярные вихри, ток смещения и свет . Издательство Чикагского университета. ISBN 978-0521353656 .

[59] Маккиннон, Ангус (2002). «Квантовые механизмы: простая механическая система в квантовом режиме». Нанотехнологии . 13 (5): 678–681. arXiv : cond-mat/0205647 . Бибкод : 2002Nanot..13..678M . дои : 10.1088/0957-4484/13/5/328 . S2CID 14994774 .

[60] Сандук, Мичиган (2007). «Подразумевает ли гипотеза трех волн скрытую структуру?» (PDF) . Апейрон . 14 (2): 113–125. Бибкод : 2007Apei...14..113S .

[61] Сандер, К. (1957), «Строение и функции прыжкового аппарата Pyrilla perpusilla WALKER (Homoptera - Fulgoridae)», Zool. Иб. Йена (Анат.) (на немецком языке), 75 : 383–388.

[Burrows-62] Jump up to: ^а ^б Берроуз, Малькольм; Саттон, Грегори (13 сентября 2013 г.). «Взаимодействующие шестерни синхронизируют движения ног прыгающего насекомого» . Наука . 341 (6151): 1254–1256. Бибкод : 2013Sci...341.1254B . дои : 10.1126/science.1240284 . hdl : 1983/69cf1502-217a-4dca-a0d3-f8b247794e92 . ПМИД 24031019 . S2CID 24640726 .

[pop-63] Херкевиц, Уильям (12 сентября 2013 г.), «Первая шестерня, обнаруженная в природе» , «Популярная механика».

[natgeo-64] Ли, Джейн Дж. (12 сентября 2013 г.), «Насекомые используют шестерни на задних лапах, чтобы прыгать» , National Geographic , заархивировано из оригинала 13 сентября 2013 г.

[Smithsonian-65] Стромберг, Джозеф (12 сентября 2013 г.), «У этого насекомого единственные механические механизмы, когда-либо найденные в природе» , журнал Smithsonian Magazine , получено 18 ноября 2020 г.

[Verge-66] Jump up to: ^а ^б Робертсон, Ади (12 сентября 2013 г.). «Первые в природе шестеренки обнаружены на ногах насекомых» . Грань . Проверено 14 сентября 2013 г.

[phys.org-67] Функционирующие «механические шестерни» впервые замечены в природе , PHYS.ORG, Кембриджский университет

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]

[ 28 ]

[ 29 ]

[ 30 ]

[ 31 ]

[ 32 ]

[ 33 ]

[ 34 ]

[ 35 ]

[ 36 ]

[ 37 ]

[ 38 ]

[ 39 ]

[ 40 ]

[ 41 ]

[ 42 ]

[ 43 ]

[ 44 ]

[ 45 ]

[ 46 ]

[ 47 ]

[ 48 ]

[ 49 ]

[ 50 ]

[ 51 ]

[ 52 ]

[ 53 ]

[ 54 ]

[ 55 ]

[ 56 ]

[ 57 ]

[ 58 ]

[ 59 ]

[ 60 ]

[ 61 ]

[ 62 ]

[ 63 ]

[ 64 ]

[ 65 ]

[ 66 ]

[ 67 ]

v т и Кинематическая пара
Lower pairs	Revolute Prismatic Cylindrical Screw Planar Spherical (ball)
Higher pairs	Cam Gears