Критическая точка (термодинамика)

Субкритический этан , жидкая и газовая фазы сосуществуют.
Критическая точка (32,17 °C, 48,72 бар), опалесценция.
Сверхкритический этан, жидкость . ^{[ 1 ]}

В термодинамике ( критическая точка или критическое состояние ) — это конечная точка кривой фазового равновесия . Одним из примеров является критическая точка жидкость-пар, конечная точка кривой давление-температура, которая обозначает условия, при которых жидкость и ее пар могут сосуществовать. При более высоких температурах газ переходит в сверхкритическую фазу и поэтому не может быть сжижен только за счет давления. В критической точке, определяемой критической температурой T _c и критическим давлением p _c , фазовые границы исчезают. Другие примеры включают критические точки жидкость-жидкость в смесях и переход ферромагнетик-парамагнетик ( температура Кюри ) в отсутствие внешнего магнитного поля. ^{[ 2 ]}

Критическая точка жидкость-пар

Обзор

Для простоты и ясности общее понятие критической точки лучше всего представить путем обсуждения конкретного примера — критической точки пар-жидкость. Это была первая обнаруженная критическая точка, и она до сих пор остается самой известной и наиболее изученной.

На рисунке показана схематическая PT -диаграмма ( чистого вещества в отличие от смесей, которые имеют дополнительные переменные состояния и более богатые фазовые диаграммы, обсуждаемые ниже). Общеизвестные фазы: твердая , жидкая и паровая, разделены фазовыми границами, т.е. комбинациями давления и температуры, при которых две фазы могут сосуществовать. В тройной точке все три фазы могут сосуществовать. Однако граница жидкость-пар заканчивается в конечной точке при некоторой критической температуре T _c и критическом давлении p _c . Это критическая точка .

Критическая точка воды наблюдается при температуре 647,096 К (373,946 ° C; 705,103 ° F) и 22,064 мегапаскаля (3200,1 фунта на квадратный дюйм; 217,75 атм; 220,64 бар). ^{[ 3 ]}

Вблизи . критической точки физические свойства жидкости и пара резко изменяются, причем обе фазы становятся еще более схожими Например, жидкая вода при нормальных условиях практически несжимаема, имеет низкий коэффициент теплового расширения, высокую диэлектрическую проницаемость и является отличным растворителем электролитов. Вблизи критической точки все эти свойства изменяются на прямо противоположные: вода становится сжимаемой, расширяемой, плохим диэлектриком , плохим растворителем для электролитов и легче смешивается с неполярными газами и органическими молекулами. ^{[ 4 ]}

В критической точке существует только одна фаза. Теплота парообразования равна нулю. имеется стационарная точка перегиба на линии постоянной температуры ( критическая изотерма На PV-диаграмме ) . Это означает, что в критической точке: ^{[ 5 ]}^{[ 6 ]}^{[ 7 ]}

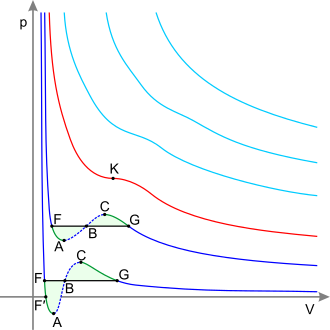
\left({\frac {\partial p}{\partial V}}\right)_{T}=0,

\left({\frac {\partial ^{2}p}{\partial V^{2}}}\right)_{T}=0.

Выше критической точки существует состояние вещества, которое непрерывно связано (может переходить без фазового перехода) как с жидким, так и с газообразным состоянием. Ее называют сверхкритической жидкостью . Распространенное из учебников знание о том, что все различия между жидкостью и паром исчезают за пределами критической точки, было оспорено Фишером и Уидомом . ^{[ 8 ]} который определил линию p – T , разделяющую состояния с разными асимптотическими статистическими свойствами ( линия Фишера – Уидома ).

Иногда ^{[ двусмысленный ]} критическая точка не проявляется в большинстве термодинамических или механических свойств, а «скрыта» и проявляется в возникновении неоднородностей модулей упругости, заметных изменениях внешнего вида и локальных свойств неаффинных капель, внезапном усилении дефектности. парная концентрация. ^{[ 9 ]}

История

Существование критической точки впервые обнаружил Шарль Каньяр де ла Тур в 1822 году. ^{[ 10 ]}^{[ 11 ]} и назван Дмитрием Менделеевым в 1860 году. ^{[ 12 ]}^{[ 13 ]} и Томас Эндрюс в 1869 году. ^{[ 14 ]} Каньяр показал, что CO ₂ можно сжижать при температуре 31°C и давлении 73 атм, но не при несколько более высокой температуре, даже при давлении до 3000 атм.

Теория

Решение вышеуказанного условия $(\partial p/\partial V)_{T}=0$ для уравнения Ван-дер-Ваальса критическую точку можно вычислить как ^{[ 5 ]}

T_{\text{c}}={\frac {8a}{27Rb}},\quad V_{\text{c}}=3nb,\quad p_{\text{c}}={\frac {a}{27b^{2}}}.

Однако уравнение Ван-дер-Ваальса, основанное на теории среднего поля , не выполняется вблизи критической точки. В частности, он предсказывает неправильные законы масштабирования .

Для анализа свойств жидкостей вблизи критической точки иногда определяются приведенные переменные состояния относительно критических свойств. ^{[ 15 ]}

T_{\text{r}}={\frac {T}{T_{\text{c}}}},\quad p_{\text{r}}={\frac {p}{p_{\text{c}}}},\quad V_{\text{r}}={\frac {V}{RT_{\text{c}}/p_{\text{c}}}}.

Принцип соответствующих состояний указывает на то, что вещества при одинаковых приведенных давлениях и температурах имеют равные приведенные объемы. Эта зависимость приблизительно верна для многих веществ, но становится все более неточной при больших значениях p _r .

Для некоторых газов существует дополнительный поправочный коэффициент, называемый поправкой Ньютона , который добавляется к рассчитанным таким образом критической температуре и критическом давлению. Это значения, полученные эмпирическим путем, и они варьируются в зависимости от интересующего диапазона давления. ^{[ 16 ]}

Таблица критической температуры и давления жидкость–пар для некоторых веществ

Вещество ^{[ 17 ]}^{[ 18 ]}	Критическая температура	Критическое давление (абсолютное)
Аргон	−122,4 ° С (150,8 К)	48,1 атм (4870 кПа)
Аммиак (NH ₃ ) ^{[ 19 ]}	132,4 °С (405,5 К)	111,3 атм (11280 кПа)
Р-134а	101,06 ° С (374,21 К)	40,06 атм (4059 кПа)
Р-410А	72,8 °С (345,9 К)	47,08 атм (4770 кПа)
Бром	310,8 °С (584,0 К)	102 атм (10300 кПа)
Цезий	1664,85 ° C (1938,00 К)	94 атм (9500 кПа)
хлор	143,8 °С (416,9 К)	76,0 атм (7700 кПа)
Этан ( C ₂ H ₆ )	31,17 °С (304,32 К)	48,077 атм (4871,4 кПа)
Этанол ( C ₂ H ₅ OH )	241 °С (514 К)	62,18 атм (6300 кПа)
Фтор	−128,85 ° С (144,30 К)	51,5 атм (5220 кПа)
Гелий	−267,96 ° С (5,19 К)	2,24 атм (227 кПа)
Водород	−239,95 ° С (33,20 К)	12,8 атм (1300 кПа)
Криптон	−63,8 ° С (209,3 К)	54,3 атм (5500 кПа)
Метан (CH ₄ )	−82,3 ° С (190,8 К)	45,79 атм (4640 кПа)
Неон	−228,75 ° С (44,40 К)	27,2 атм (2760 кПа)
Азот	−146,9 ° С (126,2 К)	33,5 атм (3390 кПа)
Кислород (О ₂ )	−118,6 ° С (154,6 К)	49,8 атм (5050 кПа)
Углекислый газ (CO ₂ )	31,04 °С (304,19 К)	72,8 атм (7380 кПа)
Закись азота (N ₂ O)	36,4 °С (309,5 К)	71,5 атм (7240 кПа)
Серная кислота (H ₂ SO ₄ )	654 °С (927 К)	45,4 атм (4600 кПа)
Ксенон	16,6 °С (289,8 К)	57,6 атм (5840 кПа)
Литий	2950 ° С (3220 К)	652 атм (66100 кПа)
Меркурий	1476,9 ° С (1750,1 К)	1720 атм (174 000 кПа)
сера	1040,85 ° C (1314,00 К)	207 атм (21000 кПа)
Железо	8227 ° С (8500 К)
Золото	6977 ° С (7250 К)	5000 атм (510 000 кПа)
Алюминий	7577 ° С (7850 К)
Вода (Н ₂ О) ^{[ 3 ]}^{[ 20 ]}	373,946 °С (647,096 К)	217,7 атм (22060 кПа)

Смеси: критическая точка жидкость-жидкость

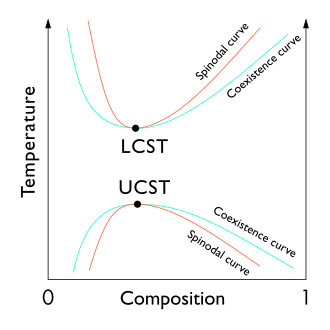
Критическая точка жидкость -жидкость раствора, возникающая при критической температуре раствора , находится на границе двухфазной области фазовой диаграммы. Другими словами, это точка, в которой бесконечно малое изменение некоторой термодинамической переменной (например, температуры или давления) приводит к разделению смеси на две отдельные жидкие фазы, как показано на фазовой диаграмме полимер-растворитель справа. Двумя типами критических точек жидкость-жидкость являются верхняя критическая температура растворения (UCST), которая является самой горячей точкой, при которой охлаждение вызывает разделение фаз, и нижняя критическая температура растворения (LCST), которая является самой холодной точкой, при которой нагревание вызывает фазовое разделение. разлука.

Математическое определение

С теоретической точки зрения критическая точка жидкость-жидкость представляет собой экстремум температуры-концентрации спинодальной кривой (как видно на рисунке справа). Таким образом, критическая точка жидкость–жидкость в двухкомпонентной системе должна удовлетворять двум условиям: условию спинодальной кривой ( вторая производная свободной энергии по концентрации должна равняться нулю) и условию экстремума ( третья производная свободной энергии по концентрации также должна быть равна нулю или производная спинодальной температуры по концентрации должна равняться нулю).

См. также

Конформная теория поля
Критический показатель
Критические явления (более продвинутая статья)
Критические точки элементов (страница данных)
Точка Кюри
Метод Джобака , метод Клинцевича , метод Лидерсена (оценка критической температуры, давления и объема по молекулярной структуре)
Критическая точка жидкость-жидкость
Более низкая критическая температура раствора
Нил-пойнт
Пороги перколяции
Фазовый переход
Неравенство Рашбрука
Масштабная инвариантность
Самоорганизованная критичность
Сверхкритическая жидкость , Сверхкритическая сушка , Сверхкритическое водное окисление , Сверхкритическая жидкостная экстракция
Трикритическая точка
Тройная точка
Верхняя критическая температура раствора
Масштабирование Видома

Ссылки

^ Хорстманн, Свен (2000). смесей жидкостей при высоком давлении для расширения уравнения группы ПСРК ] Теоретические и экспериментальные исследования фазового равновесия состояния вклада (доктор философии) (на немецком языке). Ольденбург, Германия: Ольденбургский университет Карла фон Осецкого . ISBN 3-8265-7829-5 . OCLC 76176158 .
^ Стэнли, Х. Юджин (1987). Введение в фазовые переходы и критические явления . Нью-Йорк: Издательство Оксфордского университета. ISBN 0-19-505316-8 . OCLC 15696711 .
^ Перейти обратно: ^а ^б Вагнер, В.; Прусс, А. (июнь 2002 г.). «Формулировка IAPWS 1995 года для термодинамических свойств обычного водного вещества для общего и научного использования». Журнал физических и химических справочных данных . 31 (2): 398. дои : 10.1063/1.1461829 .
^ Анисимов, Сенгерс , Левелт Сенгерс (2004): Околокритическое поведение водных систем. Глава 2 в Водная система при повышенных температурах и давлениях Палмер и др., ред. Эльзевир.
^ Перейти обратно: ^а ^б П. Аткинс и Дж. де Паула, Физическая химия, 8-е изд. (WH Freeman 2006), с. 21.
^ К.Дж. Лейдлер и Дж.Х. Мейзер, Физическая химия (Бенджамин/Каммингс 1982), стр. 27.
^ П.А. Рок, Химическая термодинамика (MacMillan 1969), стр. 123.
^ Фишер, Майкл Э.; Видом, Б. (1969). «Распад корреляций в линейных системах» . Журнал химической физики . 50 (9): 3756. Бибкод : 1969JChPh..50.3756F . дои : 10.1063/1.1671624 . Проверено 9 января 2023 г.
^ Дас, Тамогна; Гангули, Сасвати; Сенгупта, Сураджит; Рао, Мадан (3 июня 2015 г.). «Неаффинные флуктуации перед выходом и скрытая критическая точка в напряженных кристаллах» . Научные отчеты . 5 (1): 10644. Бибкод : 2015НатСР...510644Д . дои : 10.1038/srep10644 . ПМЦ 4454149 . ПМИД 26039380 .
^ Шарль Каньяр де ла Тур (1822 г.). «Изложение некоторых результатов, полученных совместным действием тепла и сжатия на некоторые жидкости, например воду, спирт, серный эфир и петролейный спирт» [Изложение некоторых результатов, полученных совместным действием тепла и сжатия на некоторые жидкости, такие как как вода, спирт, серный эфир (т.е. диэтиловый эфир) и дистиллированный петролейный спирт]. Анналы химии и физики (на французском языке). 21 : 127–132.
^ Берш, Б., Хенкель, М., Кенна, Р. (2009) Критические явления: 150 лет со дня Каньяра де ла Тура. Журнал физических исследований 13 (3), стр. 3001-1–3001-4.
^
Mendeleev called the critical point the "absolute temperature of boiling" ( Russian : абсолютная температура кипения ; German : absolute Siedetemperatur ).
- Менделеев, Д. (1861). "О расширении жидкостей от нагревания выше температуры кипения" [On the expansion of liquids from heating above the temperature of boiling]. Горный Журнал [Mining Journal] (in Russian). 4 : 141–152. The "absolute temperature of boiling" is defined on p. 151. Available at Wikimedia
- Немецкий перевод: Менделеев, Д. (1861). «О расширении жидкостей при нагревании выше температуры кипения» . Анналы химии и фармации (на немецком языке). 119 : 1–11. дои : 10.1002/jlac.18611190102 . «Абсолютная температура кипения» определена на стр. 11: « В качестве абсолютной температуры кипения мы должны считать точку, при которой 1) сцепление жидкости = 0° и ² = 0, при котором 2) скрытая теплота парообразования также = 0 и при котором 3) жидкость превращается в пар независимо от давления и объёма». (Под «абсолютной температурой кипения» следует понимать точку, при которой (1) сцепление жидкости равно 0° и a ² = 0 [ где ² – коэффициент капиллярности, р. 6], при котором (2) скрытая теплота парообразования также равна нулю и при котором (3) жидкость превращается в пар независимо от давления и объема.)
- В 1870 году Менделеев заявил против Томаса Эндрюса о своем приоритете в определении критической точки: Менделеев, Д. (1870). «Комментарии к исследованиям Эндрюса по сжимаемости углекислого газа». Анналы физики . 2-я серия (на немецком языке). 141 (12): 618–626. Бибкод : 1870АнП...217..618М . дои : 10.1002/andp.18702171218 .
^ Ландау, Лифшиц, Теоретическая физика, Том. V: Статистическая физика, Гл. 83 [немецкое издание 1984 г.].
^ Эндрюс, Томас (1869). «Бекеровская лекция: О непрерывности газообразного и жидкого состояний вещества» . Философские труды Королевского общества . 159 . Лондон: 575–590. дои : 10.1098/rstl.1869.0021 . S2CID 96898875 . Термин «критическая точка» появляется на странице 588.
^ Ценгель, Юнус А.; Болес, Майкл А. (2002). Термодинамика: инженерный подход . Бостон: МакГроу-Хилл. стр. 91–93. ISBN 978-0-07-121688-3 .
^ Маслан, Фрэнк Д.; Литтман, Теодор М. (1953). «Диаграмма сжимаемости водорода и инертных газов». Индийский англ. Хим . 45 (7): 1566–1568. дои : 10.1021/ie50523a054 .
^ Эмсли, Джон (1991). Элементы (Второе изд.). Издательство Оксфордского университета . ISBN 978-0-19-855818-7 .
^ Ценгель, Юнус А.; Болес, Майкл А. (2002). Термодинамика: инженерный подход (Четвертое изд.). МакГроу-Хилл . стр. 824 . ISBN 978-0-07-238332-4 .
^ «Аммиак – NH3 – Термодинамические свойства» . www.engineeringtoolbox.com . Проверено 7 апреля 2017 г.
^ «Критическая температура и давление» . Университет Пердью . Проверено 19 декабря 2006 г.

Дальнейшее чтение

«Пересмотренный выпуск промышленной формулы IAPWS 1997 г. для термодинамических свойств воды и пара» (PDF) . Международная ассоциация свойств воды и пара. Август 2007 года . Проверено 9 июня 2009 г.

«Критические точки для некоторых распространенных растворителей» . ПроНаукаТех. Архивировано из оригинала 31 января 2008 г.
«Критическая температура и давление» . Кафедра химии . Университет Пердью . Проверено 3 декабря 2006 г.

[1] Хорстманн, Свен (2000). смесей жидкостей при высоком давлении для расширения уравнения группы ПСРК ] Теоретические и экспериментальные исследования фазового равновесия состояния вклада (доктор философии) (на немецком языке). Ольденбург, Германия: Ольденбургский университет Карла фон Осецкого . ISBN 3-8265-7829-5 . OCLC 76176158 .

[2] Стэнли, Х. Юджин (1987). Введение в фазовые переходы и критические явления . Нью-Йорк: Издательство Оксфордского университета. ISBN 0-19-505316-8 . OCLC 15696711 .

[IAPWS95-3] Перейти обратно: ^а ^б Вагнер, В.; Прусс, А. (июнь 2002 г.). «Формулировка IAPWS 1995 года для термодинамических свойств обычного водного вещества для общего и научного использования». Журнал физических и химических справочных данных . 31 (2): 398. дои : 10.1063/1.1461829 .

[4] Анисимов, Сенгерс , Левелт Сенгерс (2004): Околокритическое поведение водных систем. Глава 2 в Водная система при повышенных температурах и давлениях Палмер и др., ред. Эльзевир.

[Atkins-5] Перейти обратно: ^а ^б П. Аткинс и Дж. де Паула, Физическая химия, 8-е изд. (WH Freeman 2006), с. 21.

[6] К.Дж. Лейдлер и Дж.Х. Мейзер, Физическая химия (Бенджамин/Каммингс 1982), стр. 27.

[7] П.А. Рок, Химическая термодинамика (MacMillan 1969), стр. 123.

[8] Фишер, Майкл Э.; Видом, Б. (1969). «Распад корреляций в линейных системах» . Журнал химической физики . 50 (9): 3756. Бибкод : 1969JChPh..50.3756F . дои : 10.1063/1.1671624 . Проверено 9 января 2023 г.

[9] Дас, Тамогна; Гангули, Сасвати; Сенгупта, Сураджит; Рао, Мадан (3 июня 2015 г.). «Неаффинные флуктуации перед выходом и скрытая критическая точка в напряженных кристаллах» . Научные отчеты . 5 (1): 10644. Бибкод : 2015НатСР...510644Д . дои : 10.1038/srep10644 . ПМЦ 4454149 . ПМИД 26039380 .

[10] Шарль Каньяр де ла Тур (1822 г.). «Изложение некоторых результатов, полученных совместным действием тепла и сжатия на некоторые жидкости, например воду, спирт, серный эфир и петролейный спирт» [Изложение некоторых результатов, полученных совместным действием тепла и сжатия на некоторые жидкости, такие как как вода, спирт, серный эфир (т.е. диэтиловый эфир) и дистиллированный петролейный спирт]. Анналы химии и физики (на французском языке). 21 : 127–132.

[11] Берш, Б., Хенкель, М., Кенна, Р. (2009) Критические явления: 150 лет со дня Каньяра де ла Тура. Журнал физических исследований 13 (3), стр. 3001-1–3001-4.

[12] Mendeleev called the critical point the "absolute temperature of boiling" ( Russian : абсолютная температура кипения ; German : absolute Siedetemperatur ).
Менделеев, Д. (1861). "О расширении жидкостей от нагревания выше температуры кипения" [On the expansion of liquids from heating above the temperature of boiling]. Горный Журнал [Mining Journal] (in Russian). 4 : 141–152. The "absolute temperature of boiling" is defined on p. 151. Available at Wikimedia

Немецкий перевод: Менделеев, Д. (1861). «О расширении жидкостей при нагревании выше температуры кипения» . Анналы химии и фармации (на немецком языке). 119 : 1–11. дои : 10.1002/jlac.18611190102 . «Абсолютная температура кипения» определена на стр. 11: « В качестве абсолютной температуры кипения мы должны считать точку, при которой 1) сцепление жидкости = 0° и ² = 0, при котором 2) скрытая теплота парообразования также = 0 и при котором 3) жидкость превращается в пар независимо от давления и объёма». (Под «абсолютной температурой кипения» следует понимать точку, при которой (1) сцепление жидкости равно 0° и a ² = 0 [ где ² – коэффициент капиллярности, р. 6], при котором (2) скрытая теплота парообразования также равна нулю и при котором (3) жидкость превращается в пар независимо от давления и объема.)

В 1870 году Менделеев заявил против Томаса Эндрюса о своем приоритете в определении критической точки: Менделеев, Д. (1870). «Комментарии к исследованиям Эндрюса по сжимаемости углекислого газа». Анналы физики . 2-я серия (на немецком языке). 141 (12): 618–626. Бибкод : 1870АнП...217..618М . дои : 10.1002/andp.18702171218 .

[13] Менделеев, Д. (1861). "О расширении жидкостей от нагревания выше температуры кипения" [On the expansion of liquids from heating above the temperature of boiling]. Горный Журнал [Mining Journal] (in Russian). 4 : 141–152. The "absolute temperature of boiling" is defined on p. 151. Available at Wikimedia

[14] Немецкий перевод: Менделеев, Д. (1861). «О расширении жидкостей при нагревании выше температуры кипения» . Анналы химии и фармации (на немецком языке). 119 : 1–11. дои : 10.1002/jlac.18611190102 . «Абсолютная температура кипения» определена на стр. 11: « В качестве абсолютной температуры кипения мы должны считать точку, при которой 1) сцепление жидкости = 0° и ² = 0, при котором 2) скрытая теплота парообразования также = 0 и при котором 3) жидкость превращается в пар независимо от давления и объёма». (Под «абсолютной температурой кипения» следует понимать точку, при которой (1) сцепление жидкости равно 0° и a ² = 0 [ где ² – коэффициент капиллярности, р. 6], при котором (2) скрытая теплота парообразования также равна нулю и при котором (3) жидкость превращается в пар независимо от давления и объема.)

[15] В 1870 году Менделеев заявил против Томаса Эндрюса о своем приоритете в определении критической точки: Менделеев, Д. (1870). «Комментарии к исследованиям Эндрюса по сжимаемости углекислого газа». Анналы физики . 2-я серия (на немецком языке). 141 (12): 618–626. Бибкод : 1870АнП...217..618М . дои : 10.1002/andp.18702171218 .

[13] Ландау, Лифшиц, Теоретическая физика, Том. V: Статистическая физика, Гл. 83 [немецкое издание 1984 г.].

[14] Эндрюс, Томас (1869). «Бекеровская лекция: О непрерывности газообразного и жидкого состояний вещества» . Философские труды Королевского общества . 159 . Лондон: 575–590. дои : 10.1098/rstl.1869.0021 . S2CID 96898875 . Термин «критическая точка» появляется на странице 588.

[15] Ценгель, Юнус А.; Болес, Майкл А. (2002). Термодинамика: инженерный подход . Бостон: МакГроу-Хилл. стр. 91–93. ISBN 978-0-07-121688-3 .

[16] Маслан, Фрэнк Д.; Литтман, Теодор М. (1953). «Диаграмма сжимаемости водорода и инертных газов». Индийский англ. Хим . 45 (7): 1566–1568. дои : 10.1021/ie50523a054 .

[17] Эмсли, Джон (1991). Элементы (Второе изд.). Издательство Оксфордского университета . ISBN 978-0-19-855818-7 .

[18] Ценгель, Юнус А.; Болес, Майкл А. (2002). Термодинамика: инженерный подход (Четвертое изд.). МакГроу-Хилл . стр. 824 . ISBN 978-0-07-238332-4 .

[19] «Аммиак – NH3 – Термодинамические свойства» . www.engineeringtoolbox.com . Проверено 7 апреля 2017 г.

[20] «Критическая температура и давление» . Университет Пердью . Проверено 19 декабря 2006 г.

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

v т и Состояния материи ( список )
Состояние	Твердый Жидкость Газ / Пар Сверхкритическая жидкость Плазма
Низкая энергия	Конденсат Бозе – Эйнштейна Фермионный конденсат Вырожденная материя Квантовый зал дело Ридберга Странное дело сверхтекучий Супертвердый Фотонная молекула
Высокая энергия	КХД имеет значение Кварк-глюонная плазма Конденсат цветного стекла
Другие штаты	Коллоид Кристалл Жидкий кристалл Кристалл времени Квантовая спиновая жидкость Экзотическая материя Программируемая материя Темная материя Антиматерия Магнитно упорядоченный Антиферромагнетик Ферримагнетик Ферромагнетик Струнная сетка жидкость Суперстекло
Фазовые переходы	Кипение Точка кипения Конденсат Критическая линия Критическая точка Кристаллизация Депонирование Испарение Мгновенное испарение Замораживание Химическая ионизация Ионизация Лямбда-точка плавление Температура плавления Рекомбинация Регулирование Насыщенная жидкость Сублимация Переохлаждение Тройная точка Испарение Витрификация
Количества	Энтальпия плавления Энтальпия сублимации Энтальпия испарения Скрытое тепло Скрытая внутренняя энергия Правило Траутона Волатильность
Концепции	Барионная материя Бинодал Сжатая жидкость Кривая охлаждения Уравнение состояния Эффект Лейденфроста Макроскопические квантовые явления Эффект Мпембы Порядок и беспорядок (физика) Спинодаль Сверхпроводимость Перегретый пар Перегрев Термодиэлектрический эффект