Моделирование атмосферной дисперсии
| Часть серии о |
| Загрязнение |
|---|
 |
Моделирование атмосферного рассеяния — это математическое моделирование того, как загрязнители воздуха рассеиваются в окружающей атмосфере . Это выполняется с помощью компьютерных программ, которые включают алгоритмы для решения математических уравнений, управляющих рассеиванием загрязняющих веществ. Модели дисперсии используются для оценки концентрации загрязнителей воздуха или токсинов в окружающей среде с подветренной стороны, выделяемых из таких источников, как промышленные предприятия, транспортное движение или случайные выбросы химических веществ. Их также можно использовать для прогнозирования будущих концентраций при конкретных сценариях (т.е. при изменении источников выбросов). Таким образом, они являются доминирующим типом модели, используемой при разработке политики в области качества воздуха. Они наиболее полезны для загрязнителей, которые рассеиваются на большие расстояния и могут вступать в реакцию в атмосфере. Для загрязнителей, которые имеют очень высокую пространственно-временную изменчивость (т.е. имеют очень большое расстояние до источника распада, такого как черный углерод ), а также для эпидемиологических исследований также используются статистические регрессионные модели землепользования.
Модели рассеивания важны для правительственных учреждений, которым поручено защищать и контролировать качество окружающего воздуха . Модели обычно используются для определения того, соответствуют ли существующие или предлагаемые новые промышленные объекты Национальным стандартам качества окружающего воздуха (NAAQS) в США и других странах. Модели также помогают в разработке эффективных стратегий контроля, направленных на сокращение выбросов вредных загрязнителей воздуха. В конце 1960-х годов Управление по контролю за загрязнением воздуха Агентства по охране окружающей среды США инициировало исследовательские проекты, которые привели к разработке моделей для использования градостроителями и транспортными планировщиками. [1] Основное и важное применение модели дисперсии дорог, ставшей результатом таких исследований, было применено к скоростной автомагистрали Спадина в Канаде в 1971 году.
Модели рассеяния в воздухе также используются службами общественной безопасности и персоналом по управлению чрезвычайными ситуациями для аварийного планирования аварийных выбросов химических веществ. Модели используются для определения последствий случайных выбросов опасных или токсичных материалов. Случайные выбросы могут привести к пожарам, разливам или взрывам, связанным с опасными материалами, такими как химические вещества или радионуклиды. Результаты моделирования рассеяния с использованием условий источника аварийного выброса в наихудшем случае и метеорологических условий могут дать оценку территорий, подвергшихся воздействию, концентраций в окружающей среде и использоваться для определения соответствующих защитных мер в случае возникновения выброса. Соответствующие защитные меры могут включать эвакуацию или укрытие людей с подветренной стороны. На промышленных объектах такая оценка последствий или планирование действий в чрезвычайных ситуациях требуется в соответствии с Законом США о чистом воздухе (CAA), закрепленным в Части 68 Раздела 40 Свода федеральных правил .
Модели дисперсии различаются в зависимости от математических методов, использованных для разработки модели, но все они требуют ввода данных, которые могут включать:
- Метеорологические условия, такие как скорость и направление ветра, степень атмосферной турбулентности (которая характеризуется так называемым «классом устойчивости» ), температура окружающего воздуха, высота до нижней точки любой инверсии наверху, которая может присутствовать, облачный покров и солнечное излучение.
- Условия источника (концентрация или количество токсинов в терминах источника выбросов или случайных выбросов ) и температура материала.
- Параметры выбросов или выбросов, такие как местоположение и высота источника, тип источника (т. е. пожар, бассейн или вентиляционная труба) и скорость на выходе , температура на выходе и массовый расход или скорость выброса.
- Высота местности в месте источника и в месте(ах)-рецепторе, например, близлежащие дома, школы, предприятия и больницы.
- Расположение, высота и ширина любых препятствий (таких как здания или другие конструкции) на пути выбрасываемого газового шлейфа, шероховатость поверхности или использование более общего параметра «сельская» или «городская» местность.
Многие современные программы моделирования рассеяния включают в себя модуль препроцессора для ввода метеорологических и других данных, а многие также включают модуль постпроцессора для построения графиков выходных данных и/или построения площадей, подвергшихся воздействию загрязнителей воздуха. карты. Участки затронутых территорий могут также включать изоплеты , показывающие области от минимальной до высокой концентрации, которые определяют области наибольшего риска для здоровья. Изоплетные графики полезны при определении защитных мер для населения и лиц, принимающих меры реагирования.
Модели атмосферной дисперсии также известны как модели атмосферной диффузии, модели дисперсии воздуха, модели качества воздуха и модели дисперсии загрязнения воздуха.
Слои атмосферы [ править ]
Обсуждение слоев земной атмосферы необходимо, чтобы понять, где в атмосфере рассеиваются переносимые по воздуху загрязнители. Слой, ближайший к поверхности Земли, известен как тропосфера . Он простирается от уровня моря до высоты около 18 км (11 миль) и содержит около 80 процентов массы всей атмосферы. Стратосфера . является следующим слоем и простирается от 18 км (11 миль) до примерно 50 км (31 миль) Третий слой — это мезосфера , простирающаяся от 50 км (31 мили) до примерно 80 км (50 миль). Есть и другие слои выше 80 км, но они несущественны с точки зрения моделирования атмосферной дисперсии.
Самая нижняя часть тропосферы называется пограничным слоем атмосферы (ABL) или планетарным пограничным слоем (PBL). Температура воздуха в атмосфере снижается с увеличением высоты, пока не достигает так называемого инверсионного слоя (где температура увеличивается с увеличением высоты), который ограничивает конвективный пограничный слой , обычно до высоты примерно от 1,5 до 2 км (от 0,93 до 1,24 мили). . Верхняя часть тропосферы (т. е. над инверсионным слоем) называется свободной тропосферой и простирается до тропопаузы (границы в атмосфере Земли между тропосферой и стратосферой). В тропических и средних широтах в дневное время слой свободной конвекции может охватывать всю тропосферу, которая составляет от 10 до 18 км (от 6,2 до 11,2 миль) в зоне внутритропической конвергенции .
ABL имеет наиболее важное значение с точки зрения выбросов, переноса и рассеивания загрязняющих веществ в воздухе. Часть АПС между поверхностью Земли и нижней частью инверсионного слоя известна как слой смешения. Практически все переносимые по воздуху загрязняющие вещества, выбрасываемые в окружающую атмосферу, переносятся и рассеиваются в слое смешения. Часть выбросов проникает через инверсионный слой и попадает в свободную тропосферу над АПС.
Таким образом, слоями земной атмосферы от поверхности земли вверх являются: ABL, состоящий из слоя смешения, перекрытого инверсионным слоем; свободная тропосфера; стратосфера; мезосфера и другие. Многие модели атмосферной дисперсии называются моделями пограничного слоя , поскольку они в основном моделируют дисперсию загрязнителей воздуха в пределах административной границы. Чтобы избежать путаницы, модели, называемые мезомасштабными моделями, имеют возможности моделирования дисперсии, простирающиеся по горизонтали до нескольких сотен километров. Это не означает, что они моделируют дисперсию в мезосфере.
загрязнителей воздуха Гауссово уравнение дисперсии
Техническая литература по рассеиванию загрязнения воздуха довольно обширна и датируется 1930-ми годами и ранее. Одно из первых уравнений дисперсии шлейфа загрязнителей воздуха было получено Бозанке и Пирсоном. [2] Их уравнение не предполагало гауссово распределение и не учитывало эффект отражения шлейфа загрязняющих веществ от земли.
Сэр Грэм Саттон вывел уравнение дисперсии шлейфа загрязнителей воздуха в 1947 году. [3] который действительно включал предположение о гауссовском распределении вертикального и бокового рассеяния шлейфа, а также учитывал эффект отражения шлейфа от земли.
Благодаря появлению строгих правил экологического контроля , в период с конца 1960-х годов по настоящее время произошел огромный рост использования расчетов рассеивания шлейфа загрязнителей воздуха. В этот период было разработано множество компьютерных программ для расчета рассеивания выбросов загрязняющих веществ в воздух, получивших название «модели рассеивания воздуха». Основой для большинства этих моделей было полное уравнение для моделирования гауссовой дисперсии непрерывных плавучих шлейфов загрязнения воздуха, показанное ниже: [4] [5]
| где: | |
| = параметр дисперсии бокового ветра | |
| = | |
| = параметр вертикальной дисперсии = | |
| = вертикальная дисперсия без отражений | |
| = | |
| = вертикальная дисперсия при отражении от земли | |
| = | |
| = вертикальная дисперсия для отражения от инверсии вверху | |
| = | |
| = концентрация выбросов, г/м³, на любом рецепторе, расположенном: | |
| x метров по ветру от точки источника выбросов | |
| y метров при боковом ветре от центральной линии шлейфа выбросов | |
| z метров над уровнем земли | |
| = интенсивность выбросов загрязняющих веществ от источника, г/с | |
| = горизонтальная скорость ветра вдоль оси шлейфа, м/с | |
| = высота осевой линии шлейфа выбросов над уровнем земли, м | |
| = вертикальное стандартное отклонение распределения выбросов, м | |
| = горизонтальное стандартное отклонение распределения выбросов, м | |
| = высота от уровня земли до нижней точки инверсии вверху, м | |
| = показательная функция |
Приведенное выше уравнение включает не только отражение вверх от земли, но также включает отражение вниз от нижней части любой инверсионной крышки, присутствующей в атмосфере.
Сумма четырех экспоненциальных членов в довольно быстро сходится к конечному значению. В большинстве случаев суммирование рядов с m = 1, m = 2 и m = 3 даст адекватное решение.
и являются функциями класса устойчивости атмосферы (т. е. меры турбулентности в окружающей атмосфере) и расстояния по ветру до объекта воздействия. Двумя наиболее важными переменными, влияющими на полученную степень дисперсии выбросов загрязняющих веществ, являются высота точки источника выбросов и степень атмосферной турбулентности. Чем больше турбулентность, тем лучше степень дисперсии.
Уравнения [6] [7] для и являются:
(x) = exp(I y + J y ln(x) + K y [ln(x)] 2 )
(x) = exp(I z + J z ln(x) + K z [ln(x)] 2 )
(единицы , и , и x указаны в метрах)
| Коэффициент | А | Б | С | Д | И | Ф |
|---|---|---|---|---|---|---|
| я да | -1.104 | -1.634 | -2.054 | -2.555 | -2.754 | -3.143 |
| да да | 0.9878 | 1.0350 | 1.0231 | 1.0423 | 1.0106 | 1.0148 |
| К й | -0.0076 | -0.0096 | -0.0076 | -0.0087 | -0.0064 | -0.0070 |
| I z | 4.679 | -1.999 | -2.341 | -3.186 | -3.783 | -4.490 |
| Дж З | -1.7172 | 0.8752 | 0.9477 | 1.1737 | 1.3010 | 1.4024 |
| К з | 0.2770 | 0.0136 | -0.0020 | -0.0316 | -0.0450 | -0.0540 |
Классификацию классов устойчивости предложил Ф. Паскиль. [8] К шести классам устойчивости относятся:А-крайне неустойчивБ-умеренно нестабильныйC-слегка нестабильныйD-нейтральныйE-слегка стабильныйF-умеренно стабильный
Полученные в результате расчеты концентраций загрязнителей воздуха часто выражаются в виде загрязнителей воздуха концентрации контурной карты , чтобы показать пространственные вариации уровней загрязнения на обширной исследуемой территории. Таким образом, контурные линии могут перекрывать чувствительные местоположения рецепторов и выявлять пространственное соотношение загрязнителей воздуха с интересующими областями.
В то время как более старые модели полагаются на классы устойчивости (см. терминологию рассеивания загрязнения воздуха ) для определения и Более поздние модели все чаще полагаются на теорию подобия Монина-Обухова для получения этих параметров.
подъема Уравнения шлейфа Бриггса
Гауссово уравнение дисперсии загрязнителей воздуха (обсуждаемое выше) требует ввода H , который представляет собой высоту центральной линии шлейфа загрязняющих веществ над уровнем земли, а H представляет собой сумму H s (фактическая физическая высота точки источника выбросов шлейфа загрязняющих веществ) плюс Δ H. (шлейм поднимается из-за плавучести шлейфа).
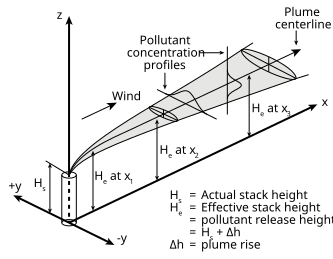
Для определения Δ H во многих, если не в большинстве моделей рассеивания воздуха, разработанных в период с конца 1960-х по начало 2000-х годов, использовались так называемые уравнения Бриггса. Г. А. Бриггс впервые опубликовал свои наблюдения и сравнения подъема шлейфа в 1965 году. [9] В 1968 году на симпозиуме, спонсируемом CONCAWE (голландская организация), он сравнил многие модели подъема шлейфа, доступные тогда в литературе. [10] В том же году Бриггс также написал раздел публикации под редакцией Слэйда. [11] занимается сравнительным анализом моделей подъема шлейфа. За этим последовал в 1969 году его классический критический обзор всей литературы о подъеме шлейфа: [12] в котором он предложил набор уравнений подъема шлейфа, которые стали широко известны как «уравнения Бриггса». Впоследствии Бриггс модифицировал свои уравнения подъема шлейфа 1969 года в 1971 и 1972 годах. [13] [14]
Бриггс разделил шлейфы загрязнения воздуха на четыре основные категории:
- Холодные струи шлейфов в условиях спокойного окружающего воздуха
- Шлейфы холодных струй в ветреных условиях окружающего воздуха
- Горячие плавучие шлейфы в условиях спокойного окружающего воздуха.
- Горячие плавучие шлейфы в ветреных условиях
Бриггс считал, что в траектории шлейфов холодных струй доминирует их начальный импульс скорости, а в траектории горячих плавучих шлейфов доминирует их плавучий импульс до такой степени, что их начальный импульс скорости был относительно неважен. Хотя Бриггс предложил уравнения подъема шлейфа для каждой из вышеупомянутых категорий шлейфа, важно подчеркнуть, что «уравнения Бриггса», которые стали широко использоваться, - это те, которые он предложил для наклоненных, горячих плавучих шлейфов.
В целом, уравнения Бриггса для изогнутых горячих плавучих шлейфов основаны на наблюдениях и данных, касающихся шлейфов от типичных источников горения, таких как дымовые трубы паровых котлов, сжигающих ископаемое топливо на крупных электростанциях. Таким образом, скорости на выходе из дымохода, вероятно, находились в диапазоне от 20 до 100 футов/с (от 6 до 30 м/с), а температура на выходе - от 250 до 500 °F (от 120 до 260 °C).
Логическая схема использования уравнений Бриггса [4] для получения траектории подъема загнутых плавучих шлейфов представлена ниже:
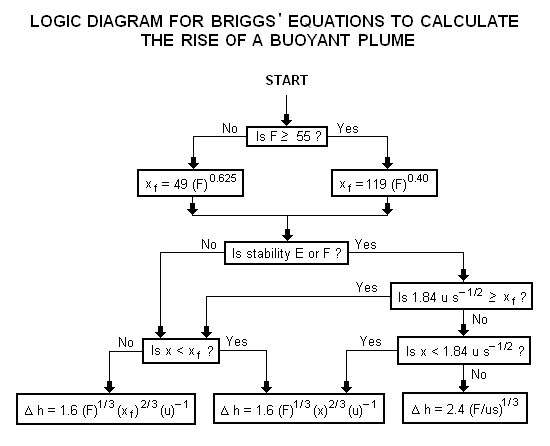
где: Δh = высота шлейфа, м Ф = коэффициент плавучести, м 4 с −3 х = расстояние по ветру от источника шлейфа, м х ж = расстояние по ветру от источника шлейфа до точки максимального подъема шлейфа, м в = скорость ветра на фактической высоте штабеля, м/с с = параметр устойчивости, с −2
Вышеуказанные параметры, используемые в уравнениях Бриггса, обсуждаются в книге Бейчка. [4]
См. также [ править ]
Модели дисперсии атмосферной
Список моделей атмосферной дисперсии представляет собой более полный список моделей, чем приведенный ниже. В нем содержится очень краткое описание каждой модели.


Организации [ править ]
- Группа моделирования качества воздуха
- Лаборатория воздушных ресурсов
- Финский метеорологический институт
- KNMI, Королевский голландский метеорологический институт
- Национальный институт экологических исследований Дании
- Шведский метеорологический и гидрологический институт
- СДЕЛАЙТЕ ДЫХАНИЕ
- Комитет по связи Великобритании по моделированию атмосферной дисперсии
- Британское бюро моделирования дисперсии
- Институт исследования пустынь
- VITO (институт) Бельгия; https://vito.be/en
- Шведское агентство оборонных исследований , FOI
Другие [ править ]
- Терминология рассеивания загрязнения воздуха
- Список моделей атмосферной дисперсии
- Портативная система измерения выбросов (PEMS)
- Моделирование рассеивания воздуха на проезжей части
- Полезные преобразования и формулы для моделирования рассеивания воздуха.
- Прогнозирование загрязнения воздуха
Ссылки [ править ]
- ^ Фенстерсток, Дж. К. и др., «Снижение потенциального загрязнения воздуха посредством экологического планирования» [ постоянная мертвая ссылка ] , JAPCA, Том 21, № 7, 1971.
- ^ Босанке, Ч. Х. и Пирсон, Дж. Л., «Распространение дыма и газов из дымоходов», Пер. Фарадей Соц., 32:1249, 1936 г.
- ^ Саттон, О.Г., «Проблема диффузии в нижних слоях атмосферы», QJRMS, 73:257, 1947 и «Теоретическое распределение переносимых по воздуху загрязнений из фабричных дымоходов», QJRMS, 73:426, 1947.
- ↑ Перейти обратно: Перейти обратно: а б с Бейчок, Милтон Р. (2005). Основы рассеивания дымовых газов (4-е изд.). опубликовано автором. ISBN 0-9644588-0-2 .
- ^ Тернер, Д.Б. (1994). Справочник по оценкам атмосферной дисперсии: введение в моделирование дисперсии (2-е изд.). ЦРК Пресс. ISBN 1-56670-023-Х .
- ^ Сейнфельд, Джон Х. (2006). «Глава 18». Химия и физика атмосферы: от загрязнения воздуха до изменения климата . Уайли. ISBN 9780471720171 .
- ^ Ханна, Стивен (1982). «Справочник по атмосферной диффузии» . Отчет Министерства энергетики США .
- ^ В. Клюг (апрель 1984 г.). Атмосферная диффузия (3-е издание). Ф. Паскуилл и Ф. Б. Смит. Эллис Хорвуд, (John Wiley & Sons) Чичестер, 1983 (3-е изд.). Нью-Йорк: Ежеквартальный журнал Королевского метеорологического общества.
- ^ Бриггс, Джорджия, «Модель подъема шлейфа по сравнению с наблюдениями», JAPCA, 15: 433–438, 1965.
- ^ Бриггс, Джорджия, «Встреча CONCAWE: обсуждение сравнительных последствий различных формул повышения шлейфа», Atmos. Окружающая среда, 2: 228–232, 1968 г.
- ^ Слэйд, Д.Х. (редактор), «Метеорология и атомная энергия, 1968 г.», Лаборатория воздушных ресурсов, Министерство торговли США, 1968 г.
- ^ Бриггс, Джорджия, "Подъем шлейфа", Серия критических обзоров USAEC, 1969.
- ^ Бриггс, Джорджия, «Некоторые недавние анализы наблюдения за подъемом шлейфа», Proc. Второй Интернационал. Конгресс чистого воздуха, Academic Press, Нью-Йорк, 1971 г.
- ^ Бриггс, Джорджия, «Дискуссия: шлейфы дымохода в нейтральной и стабильной среде», Atmos. Окружающая среда, 6:507–510, 1972.
Дальнейшее чтение [ править ]
Книги [ править ]
- Вводный
- Бейчок, Милтон Р. (2005). Основы рассеивания дымовых газов (4-е изд.). опубликовано автором. ISBN 0-9644588-0-2 .
- Центр безопасности химических процессов (1999). Руководство по количественному анализу рисков химических процессов (2-е изд.). Американский институт инженеров-химиков, Нью-Йорк, штат Нью-Йорк. ISBN 978-0-8169-0720-5 .
- Центр безопасности химических процессов (1996). Рекомендации по использованию моделей облаков паров и источников дисперсии с рабочими примерами (2-е изд.). Американский институт инженеров-химиков, Нью-Йорк, штат Нью-Йорк. ISBN 978-0-8169-0702-1 .
- Шнелле, Карл Б. и Дей, Парта Р. (1999). Руководство по соблюдению требований к моделированию атмосферной дисперсии (1-е изд.). МакГроу-Хилл Профессионал. ISBN 0-07-058059-6 .
- Тернер, Д.Б. (1994). Рабочая тетрадь по оценкам атмосферной дисперсии: введение в моделирование дисперсии (2-е изд.). ЦРК Пресс. ISBN 1-56670-023-Х .
- Передовой
- Арья, С. Пал (1998). Метеорология и дисперсия загрязнения воздуха (1-е изд.). Издательство Оксфордского университета. ISBN 0-19-507398-3 .
- Баррат, Род (2001). Моделирование атмосферной дисперсии (1-е изд.). Публикации Earthscan. ISBN 1-85383-642-7 .
- Коллс, Джереми (2002). Загрязнение воздуха (1-е изд.). Спон Пресс (Великобритания). ISBN 0-415-25565-1 .
- Купер-младший, Рэндл К., Сох Р.Г. (2003). Радиоактивные выбросы в окружающую среду (1-е изд.). Джон Уайли и сыновья. ISBN 0-471-89924-0 .
- Европейский центр технологической безопасности (1999). Атмосферная дисперсия (1-е изд.). Регби: Институт инженеров-химиков. ISBN 0-85295-404-2 .
- Годиш, Тад (2003). Качество воздуха (4-е изд.). ЦРК Пресс. ISBN 1-56670-586-Х .
- Ханна, С.Р. и Дривас, Д.Г. (1996). Руководство по использованию моделей дисперсии облаков пара (2-е изд.). Уайли-Американский институт инженеров-химиков. ISBN 0-8169-0702-1 .
- Ханна, С.Р. и Стримайтис, Д.Г. (1989). Сборник тестовых примеров для моделей дисперсии источников облаков пара (1-е изд.). Центр безопасности химических процессов, Американский институт инженеров-химиков. ISBN 0-8169-0455-3 .
- Ханна, SR и Бриттер, RE (2002). Ветровой поток и рассеивание паровых облаков на промышленных и городских объектах (1-е изд.). Уайли-Американский институт инженеров-химиков. ISBN 0-8169-0863-Х .
- Перианез, Рауль (2005). Моделирование рассеяния радионуклидов в морской среде: введение (1-е изд.). Спрингер. ISBN 3-540-24875-7 .
- Пилке, Роджер А. (2001). Мезомасштабное моделирование (2-е изд.). Эльзевир. ISBN 0-12-554766-8 .
- Заннетти, П. (1990). Моделирование загрязнения воздуха: теории, вычислительные методы и доступное программное обеспечение . Ван Ностранд Рейнхольд. ISBN 0-442-30805-1 .
Материалы [ править ]
- Фораго И., Георгиев К., Хаваси А., ред. (2004). Достижения в моделировании загрязнения воздуха для экологической безопасности (семинар НАТО) . Спрингер, 2005. ISSN 0957-4352 .
- Кречмар Дж.Г., Коземанс Г., ред. (1996). Гармонизация моделирования атмосферной дисперсии для целей регулирования (4-й семинар) . Международный журнал окружающей среды и загрязнения, том. 8 нет. 3–6, Interscience Enterprises, 1997. ISSN 0957-4352 .
- Барцис, Дж. Г., изд. (1998). Гармонизация моделирования атмосферной дисперсии для целей регулирования (5-й семинар) . Международный журнал окружающей среды и загрязнения, том. 14 нет. 1–6, Interscience Enterprises, 2000. ISSN 0957-4352 .
- Коппалле, А., изд. (1999). Гармонизация моделирования атмосферной дисперсии для целей регулирования (6-й семинар) . Международный журнал окружающей среды и загрязнения, том. 16 нет. 1–6, Inderscience Enterprises, 2001. ISSN 0957-4352 .
- Бачварова Е., изд. (2002). Гармонизация моделирования атмосферной дисперсии для целей регулирования (8-й семинар) . Международный журнал окружающей среды и загрязнения, том. 20 нет. 1–6, Inderscience Enterprises, 2003. ISSN 0957-4352 .
- Суппан, П., изд. (2004). Гармонизация моделирования атмосферной дисперсии для целей регулирования (8-й семинар) . Международный журнал окружающей среды и загрязнения, том. 24 нет. 1–6 и том 25 нет. 1–6, Inderscience Enterprises, 2005. ISSN 0957-4352 .
- Занетти, П., изд. (1993). Международная конференция по загрязнению воздуха (1-я, Мехико) . Вычислительная механика, 1993. ISBN. 1-56252-146-2 .
- Де Виспелер, К., изд. (1980). Международное техническое совещание по моделированию загрязнения воздуха и его применению (11-е) . Пленум Пресс, 1981. ISBN. 0-306-40820-1 .
- Де Виспелер, К., изд. (1982). Международное техническое совещание по моделированию загрязнения воздуха и его применению (13-е) . Комитет НАТО по вызовам современного общества [от] Plenum Press, 1984. ISBN 0-306-41491-0 .
- Грининг, С.; Ширмейр, Ф.А., ред. (1995). Международное техническое совещание по моделированию загрязнения воздуха и его применению (21-е) . Комитет НАТО по вызовам современного общества [от] Plenum Press, 1996. ISBN 0-306-45381-9 .
- Грининг, С.; Шомерлиак, Н., ред. (1997). Международное техническое совещание по моделированию загрязнения воздуха и его применению (22-е) . Комитет НАТО по вызовам современного общества [от] Plenum Press, 1998. ISBN 0-306-45821-7 .
- Грининг, С.; Бачварова Е., ред. (1998). Международное техническое совещание по моделированию загрязнения воздуха и его применению (23-е) . Комитет НАТО по вызовам современного общества [автор] Kluwer Academic/Plenum Press, 2000. ISBN 0-306-46188-9 .
- Грининг, С.; Ширмейр, Ф.А., ред. (2000). Международное техническое совещание по моделированию загрязнения воздуха и его применению (24-е) . Комитет НАТО по вызовам современного общества [автор] Kluwer Academic, 2001. ISBN 0-306-46534-5 .
- Боррего, К.; Шайес, Г., ред. (2000). Международное техническое совещание по моделированию загрязнения воздуха и его применению (25-е) . Комитет НАТО по вызовам современного общества [автор] Kluwer Academic, 2002. ISBN 0-306-47294-5 .
- Боррего, К.; Инчечик С., ред. (2003). Международное техническое совещание по моделированию загрязнения воздуха и его применению (26-е) . Комитет НАТО по вызовам современного общества [автор] Kluwer Academic/Plenum Press, 2004. ISBN 0-306-48464-1 .
- Комитет по атмосферному рассеянию выбросов опасных материалов, Национальный исследовательский совет, изд. (2002). Отслеживание и прогнозирование атмосферного рассеяния выбросов опасных материалов (семинар) . Издательство национальных академий, 2003. ISBN. 0-309-08926-3 .
Руководство [ править ]
- Ханна, СР; Бриггс, Г.А. и Хоскер, Р.П. (1982). Справочник по атмосферной диффузии . Министерство энергетики США, Центр технической информации. DOE/TIC-11223. ОСТИ 5591108 .
- Агентство по охране окружающей среды США (1993). Руководство по применению уточненных моделей дисперсии опасных/токсичных выбросов в воздух . Управление планирования и стандартов качества воздуха, EPA-454/R-93-002.
- Агентство по охране окружающей среды США (1999). Руководство по программе управления рисками для анализа последствий за пределами площадки (приложения) (PDF) . Управление по твердым отходам и реагированию на чрезвычайные ситуации, EPA 550-B-99-009. Архивировано из оригинала (PDF) 17 апреля 2010 г. Проверено 9 апреля 2010 г.
- Агентство по охране окружающей среды США (1999). Технический справочный документ для анализа последствий за пределами объекта для безводного аммиака, водного аммиака, хлора и диоксида серы (PDF) . Управление готовности и предотвращения химических аварий.
- Агентство по охране окружающей среды США (2009 г.). Глава 4: Анализ последствий за пределами объекта. В Общем руководстве по программам управления рисками для предотвращения химических аварий (40 CFR, часть 68) (PDF) . Управление по твердым отходам и реагированию на чрезвычайные ситуации, EPA 555-B-04-001.
Внешние ссылки [ править ]
- Центр поддержки нормативного моделирования атмосферы Агентства по охране окружающей среды
- Группа моделирования качества воздуха Агентства по охране окружающей среды (AQMG)
- Лаборатория воздушных ресурсов NOAA (ARL)
- Веб-сайт Комитета по связи Великобритании по моделированию атмосферной дисперсии
- Веб-сайт Британского бюро моделирования дисперсии
- Транспортная модель химии атмосферы LOTOS-EUROS
- Модель OPS по оперативным приоритетным веществам (на голландском языке)
- HAMS-GPS Дисперсионное моделирование
- Wiki по моделированию атмосферной дисперсии . Адресуется международному сообществу разработчиков моделей атмосферной дисперсии – в первую очередь исследователям, но также и пользователям моделей. Его цель – объединить опыт, полученный разработчиками моделей дисперсии в ходе их работы.


![{\displaystyle \exp \;[-\,y^{2}/\,(2\;\sigma _{y}^{2}\;)\;]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8925630e3b8de6be025fb258aa809189a852082)



![{\displaystyle \;\exp \;[-\,(zH)^{2}/\,(2\;\sigma _{z}^{2}\;)\;]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32be81e17b8659fb72ef85e886a95c57401160bd)

![{\displaystyle \;\exp \;[-\,(z+H)^{2}/\,(2\;\sigma _{z}^{2}\;)\;]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8359e355bf985dc7714abecb7a250155e07b62f)

![{\displaystyle \sum _{m=1}^{\infty }\;{\big \{}\exp \;[-\,(zH-2mL)^{2}/\,(2\;\sigma _{z}^{2}\;)\;]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37cb296347f56a0618c59d247cbf00125fc3de8c)
![{\displaystyle +\,\exp \;[-\,(z+H+2mL)^{2}/\,(2\;\sigma _{z}^{2}\;)\;]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8546ac2627ada5bfebad51a692c902206a5efa2c)
![{\displaystyle +\,\exp \;[-\,(z+H-2mL)^{2}/\,(2\;\sigma _{z}^{2}\;)\;]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fe6a89e17f16835d86e8d9a8971a74db46d1e4b)
![{\displaystyle +\,\exp \;[-\,(z-H+2mL)^{2}/\,(2\;\sigma _{z}^{2}\;)\;]{\ большой \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ff94c96673914895d6e0a6d2643dca0e9e4bc77)









