Управляемый

В математике операда , каждая из которых имеет фиксированное конечное число входов ( — это структура, состоящая из абстрактных операций аргументов) и один выход, а также спецификацию того, как составлять эти операции. Учитывая операду $O$, определяется алгебра над $O$ быть множеством вместе с конкретными операциями над этим множеством, которые ведут себя точно так же, как абстрактные операции $O$. Например, есть операда Лия $L$ такие, что алгебры над $L$ являются в точности алгебрами Ли ; в некотором смысле $L$ абстрактно кодирует операции, общие для всех алгебр Ли. Операда относится к своим алгебрам так же, как группа относится к своим групповым представлениям .

История

Операды происходят из алгебраической топологии ; они были введены для характеристики итерированных пространств петель Дж . Майклом Бордманом и Райнером М. Фогтом в 1968 году. и Дж. Питера Мэя в 1972 году.

Мартин Маркл, Стив Шнайдер и Джим Сташефф пишут в своей книге об операдах:

«Имя операда и формальное определение впервые появляются в начале 1970-х годов в книге Дж. Питера Мэя «Геометрия итерированных пространств циклов», но годом или более ранее Бордман и Фогт описали ту же концепцию под названием категорий операторов в стандарте. form , вдохновленный PROP и PACT Адамса и Мак Лейна. На самом деле, существует множество предыстории. Вейбель [Вэй] указывает, что эта концепция впервые возникла сто лет назад в А. Н. Уайтхеда «Трактате об универсальной алгебре» . 1898 год».

Слово «операда» было создано Мэем как сочетание слов «операции» и « монада » (а также потому, что его мать была оперной певицей).

Интерес к операдам значительно возобновился в начале 90-х годов, когда на основе ранних идей Максима Концевича Виктор Гинзбург и Михаил Капранов обнаружили, что некоторые двойственности явления в теории рациональной гомотопии можно объяснить с помощью Кошуля . двойственности операд Операды с тех пор нашли множество применений, таких как деформационное квантование многообразий Пуассона , гипотеза Делиня , или графов гомологии в работах Максима Концевича и Томаса Вильвахера .

Интуиция

Предполагать $X$ это набор и для $n\in \mathbb {N}$ мы определяем

$P(n):=\{f:X^{n}\to X\}$,

набор всех функций из декартова произведения $n$ копии $X$ к $X$.

Мы можем составить эти функции: учитывая $f\in P(n)$, $f_{1}\in P(k_{1}),\ldots ,f_{n}\in P(k_{n})$, функция

$f\circ (f_{1},\ldots ,f_{n})\in P(k_{1}+\cdots +k_{n})$

определяется следующим образом: учитывая $k_{1}+\cdots +k_{n}$ аргументы от $X$, мы разделим их на $n$ блоки, первый из которых имеет $k_{1}$ аргументы, второй $k_{2}$ аргументы и т. д., а затем применить $f_{1}$ до первого блока, $f_{2}$ ко второму блоку и т. д. Затем мы применяем $f$ в список $n$ значения, полученные из $X$ таким образом.

Мы также можем переставлять аргументы, т.е. у нас есть правильное действие. $*$ симметрической группы $S_{n}$ на $P(n)$, определяемый

$(f*s)(x_{1},\ldots ,x_{n})=f(x_{s^{-1}(1)},\ldots ,x_{s^{-1}(n)})$

для $f\in P(n)$, $s\in S_{n}$ и $x_{1},\ldots ,x_{n}\in X$.

Приведенное ниже определение симметричной операды отражает основные свойства этих двух операций. $\circ$ и $*$.

Определение

Несимметричная операда

Несимметричная операда (иногда называемая операдой без перестановок или несимметричной операдой). $\Sigma$ или простая операда) состоит из следующего:

• последовательность $(P(n))_{n\in \mathbb {N} }$ множеств, элементы которых называются $n$и операции ,
• элемент $1$ в $P(1)$ называется личностью ,
• для всех положительных целых чисел $n$, ${\textstyle k_{1},\ldots ,k_{n}}$, композиции функция

${\begin{aligned}\circ :P(n)\times P(k_{1})\times \cdots \times P(k_{n})&\to P(k_{1}+\cdots +k_{n})\\(\theta ,\theta _{1},\ldots ,\theta _{n})&\mapsto \theta \circ (\theta _{1},\ldots ,\theta _{n}),\end{aligned}}$

удовлетворяющие следующим аксиомам когерентности:

• личность : $\theta \circ (1,\ldots ,1)=\theta =1\circ \theta$
• ассоциативность :

${\begin{aligned}&\theta \circ {\Big (}\theta _{1}\circ (\theta _{1,1},\ldots ,\theta _{1,k_{1}}),\ldots ,\theta _{n}\circ (\theta _{n,1},\ldots ,\theta _{n,k_{n}}){\Big )}\\={}&{\Big (}\theta \circ (\theta _{1},\ldots ,\theta _{n}){\Big )}\circ (\theta _{1,1},\ldots ,\theta _{1,k_{1}},\ldots ,\theta _{n,1},\ldots ,\theta _{n,k_{n}})\end{aligned}}$

Симметричная операда

Симметричная операда (часто называемая просто операдой ) — это несимметричная операда. $P$ как и выше, вместе с правым действием симметрической группы $S_{n}$ на $P(n)$ для $n\in \mathbb {N}$, обозначенный $*$ и удовлетворение

• эквивариантность : учитывая перестановку $t\in S_{n}$,

$(\theta *t)\circ (\theta _{1},\ldots ,\theta _{n})=(\theta \circ (\theta _{t(1)},\ldots ,\theta _{t(n)}))*t'$

(где $t'$ в правой части относится к элементу $S_{k_{1}+\dots +k_{n}}$ который действует на съемочной площадке $\{1,2,\dots ,k_{1}+\dots +k_{n}\}$ разбив его на $n$ блоки, первые по размеру $k_{1}$, второй по размеру $k_{2}$, через $n$размер блока $k_{n}$, а затем переставляет их местами $n$ блокирует по $t$, сохраняя каждый блок нетронутым)

и учитывая $n$ перестановки $s_{i}\in S_{k_{i}}$,

$\theta \circ (\theta _{1}*s_{1},\ldots ,\theta _{n}*s_{n})=(\theta \circ (\theta _{1},\ldots ,\theta _{n}))*(s_{1},\ldots ,s_{n})$

(где $(s_{1},\ldots ,s_{n})$ обозначает элемент $S_{k_{1}+\dots +k_{n}}$ который переставляет первый из этих блоков на $s_{1}$, второй по $s_{2}$и т. д. и сохраняет их общий порядок).

Действия перестановки в этом определении жизненно важны для большинства приложений, включая исходное приложение для зацикливания пространств.

Морфизмы

Морфизм операд $f:P\to Q$ состоит из последовательности

$(f_{n}:P(n)\to Q(n))_{n\in \mathbb {N} }$

что:

• сохраняет идентичность: $f(1)=1$
• сохраняет композицию: для каждой n -арной операции $\theta$ и операции $\theta _{1},\ldots ,\theta _{n}$,

$f(\theta \circ (\theta _{1},\ldots ,\theta _{n}))=f(\theta )\circ (f(\theta _{1}),\ldots ,f(\theta _{n}))$

• сохраняет действия перестановки: $f(x*s)=f(x)*s$.

Таким образом, операды образуют категорию , обозначаемую ${\mathsf {Oper}}$.

В других категориях

До сих пор операды рассматривались только в категории множеств. можно определить операды в любой симметричной моноидальной категории C. В более общем смысле , В этом случае каждый $P(n)$ является объектом C , композиция $\circ$ является морфизмом $P(n)\otimes P(k_{1})\otimes \cdots \otimes P(k_{n})\to P(k_{1}+\cdots +k_{n})$ в C (где $\otimes$ обозначает тензорное произведение моноидальной категории), а действия элементов симметрической группы задаются изоморфизмами в C .

Типичным примером является категория топологических пространств и непрерывных карт, где моноидальное произведение задается декартовым произведением . В этом случае топологическая операда задается последовательностью пространств (а не множеств) $\{P(n)\}_{n\geq 0}$. Структурные отображения операды (состав и действия симметрических групп) при этом считаются непрерывными. Результат называется топологической операдой . Аналогично, при определении морфизма операд необходимо было бы предположить, что рассматриваемые отображения непрерывны.

Другие общие настройки для определения операд включают, например, модули над коммутативным кольцом , цепные комплексы , группоиды (или даже сами категории категорий), коалгебры и т. д.

Алгебраистское определение

Для коммутативного кольца R рассмотрим категорию $R{\text{-}}{\mathsf {Mod}}$ модулей над R . Операду . над R можно определить как моноидный объект $(T,\gamma ,\eta )$ в моноидальной категории эндофункторов на $R{\text{-}}{\mathsf {Mod}}$ (это монада ), удовлетворяющая некоторому условию конечности.

Например, моноидный объект в категории «полиномиальные эндофункторы» на $R{\text{-}}{\mathsf {Mod}}$ это операда. Аналогично, симметричную операду можно определить как моноидный объект в категории $\mathbb {S}$-объекты , где $\mathbb {S}$ означает симметричную группу. Моноидный объект в категории комбинаторных видов — это операда в конечных множествах.

Операду в указанном выше смысле иногда рассматривают как обобщенное кольцо . Например, Николай Дуров определяет свои обобщенные кольца как моноидные объекты в моноидальной категории эндофункторов на ${\textbf {Set}}$ которые коммутируют с отфильтрованными копределами. Это обобщение кольца, поскольку каждое обычное кольцо R определяет монаду $\Sigma _{R}:{\textbf {Set}}\to {\textbf {Set}}$ который отправляет набор X в базовый набор свободного R -модуля $R^{(X)}$ созданный X. ​

Понимание аксиом

Аксиома ассоциативности

«Ассоциативность» означает, что композиция операций ассоциативна. (функция $\circ$ ассоциативен), аналогичный аксиоме теории категорий, согласно которой $f\circ (g\circ h)=(f\circ g)\circ h$; это не операции означает, что сами ассоциативны как операции. Сравните с ассоциативной операдой ниже.

Ассоциативность в теории операд означает, что выражения могут быть написаны с использованием операций без двусмысленности из пропущенных составов, точно так же, как ассоциативность операций позволяет записывать продукты без двусмысленности из опущенных скобок.

Например, если $\theta$ — это бинарная операция, которая записывается как $\theta (a,b)$ или $(ab)$. Так что $\theta$ может быть или не быть ассоциативным.

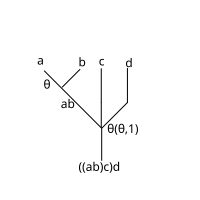
Тогда то, что обычно пишут $((ab)c)$ однозначно записывается операдически как $\theta \circ (\theta ,1)$ . Это отправляет $(a,b,c)$ к $(ab,c)$ (применять $\theta$ на первых двух и тождество на третьем), а затем $\theta$ слева "умножается" $ab$ к $c$. Это становится яснее, если изобразить его в виде дерева:

что дает 3-арную операцию:

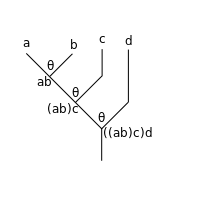
Однако выражение $(((ab)c)d)$ неоднозначно априори : это может означать $\theta \circ ((\theta ,1)\circ ((\theta ,1),1))$, если сначала исполняются внутренние композиции, или это может означать $(\theta \circ (\theta ,1))\circ ((\theta ,1),1)$, если первыми выполняются внешние композиции (операции читаются справа налево). Письмо $x=\theta ,y=(\theta ,1),z=((\theta ,1),1)$, Это $x\circ (y\circ z)$ против $(x\circ y)\circ z$. То есть в дереве отсутствуют «вертикальные скобки»:

Если первыми составляются две верхние строки операций (ставится верхняя скобка в начале $(ab)c\ \ d$ линия; сначала выполняет внутреннюю композицию), следующие результаты:

который затем однозначно оценивается и дает 4-арную операцию. В качестве аннотированного выражения:

$\theta _{(ab)c\cdot d}\circ ((\theta _{ab\cdot c},1_{d})\circ ((\theta _{a\cdot b},1_{c}),1_{d}))$

Если первыми составляются две нижние строки операций (ставится нисходящая скобка в начале $ab\quad c\ \ d$ линия; сначала делает внешнюю композицию), следующие результаты:

который затем однозначно вычисляет 4-арную операцию:

Аксиома операды ассоциативности состоит в том, что они дают один и тот же результат , и, следовательно, выражение $(((ab)c)d)$ является однозначным.

Аксиома тождества

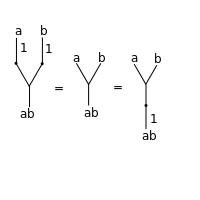
Аксиому идентичности (для бинарной операции) можно представить в виде дерева как:

это означает, что три полученные операции равны: до- или пост-компоновка с идентификатором не имеет значения. Что касается категорий, $1\circ 1=1$ является следствием аксиомы тождества.

Примеры

Операда эндоморфизмов в множествах и операдных алгебрах

Самые основные операды приведены выше в разделе «Интуиция». Для любого набора $X$, получаем операду эндоморфизма ${\mathcal {End}}_{X}$ состоящий из всех функций $X^{n}\to X$. Эти операды важны, поскольку они служат для определения операдных алгебр . Если ${\mathcal {O}}$ является операдой, операдной алгеброй над ${\mathcal {O}}$ дано набором $X$ и операдный морфизм ${\mathcal {O}}\to {\mathcal {End}}_{X}$. Интуитивно такой морфизм превращает каждую «абстрактную» операцию ${\mathcal {O}}(n)$ в «бетон» $n$-арная операция на множестве $X$. Оперированная алгебра над ${\mathcal {O}}$ таким образом, состоит из набора $X$ вместе с конкретными операциями по $X$ которые следуют правилам, абстрактно заданным операдой ${\mathcal {O}}$.

Операда эндоморфизмов в векторных пространствах и операдных алгебрах

Если k — поле , мы можем рассмотреть категорию конечномерных векторных пространств над k ; это становится моноидальной категорией, используя обычное тензорное произведение по k. Затем мы можем определить операды эндоморфизмов в этой категории следующим образом. Пусть V — конечномерное векторное пространство. Операда эндоморфизма ${\mathcal {End}}_{V}=\{{\mathcal {End}}_{V}(n)\}$ из V состоит

1. ${\mathcal {End}}_{V}(n)$ = пространство линейных отображений $V^{\otimes n}\to V$,
2. (состав) дано $f\in {\mathcal {End}}_{V}(n)$, $g_{1}\in {\mathcal {End}}_{V}(k_{1})$, ..., $g_{n}\in {\mathcal {End}}_{V}(k_{n})$, их состав задан картой $V^{\otimes k_{1}}\otimes \cdots \otimes V^{\otimes k_{n}}\ {\overset {g_{1}\otimes \cdots \otimes g_{n}}{\longrightarrow }}\ V^{\otimes n}\ {\overset {f}{\to }}\ V$,
3. (идентичность) Элемент идентификации в ${\mathcal {End}}_{V}(1)$ это карта личности $\operatorname {id} _{V}$,
4. (симметричное групповое действие) $S_{n}$ действует на ${\mathcal {End}}_{V}(n)$ переставляя компоненты тензоров в $V^{\otimes n}$.

Если ${\mathcal {O}}$ — операда, k -линейная операдная алгебра над ${\mathcal {O}}$ задается конечномерным векторным пространством V над k и операдным морфизмом ${\mathcal {O}}\to {\mathcal {End}}_{V}$; это равносильно указанию конкретных полилинейных операций над V , которые ведут себя как операции ${\mathcal {O}}$. (Обратите внимание на аналогию между операдами и операдными алгебрами и кольцами и модулями: модуль над кольцом R задается абелевой группой M вместе с кольцевым гомоморфизмом $R\to \operatorname {End} (M)$.)

В зависимости от приложений возможны вариации вышеизложенного: например, в алгебраической топологии вместо векторных пространств и тензорных произведений между ними используются (разумные) топологические пространства и декартовы произведения между ними.

Операды «Кое-что»

Оперная композиция в небольшой двухдисковой операде, поясненная в тексте.

Маленькая двухдисковая операда — это топологическая операда, в которой $P(n)$ состоит из упорядоченных списков из n непересекающихся дисков внутри диска единичного $\mathbb {R} ^{2}$ сосредоточено в начале координат. Симметричная группа действует на такие конфигурации, переставляя список маленьких дисков. Оперная композиция для дисков изображена на рисунке справа, где элемент $\theta \in P(3)$ состоит из элемента $(\theta _{1},\theta _{2},\theta _{3})\in P(2)\times P(3)\times P(4)$ чтобы получить элемент $\theta \circ (\theta _{1},\theta _{2},\theta _{3})\in P(9)$ полученный путем сжатия конфигурации $\theta _{i}$ и вставив его в i-й диск $\theta$, для $i=1,2,3$.

Аналогично можно определить маленькую операду из n-дисков , рассматривая конфигурации непересекающихся n -шаров внутри единичного шара $\mathbb {R} ^{n}$.

Первоначально операда маленьких n-кубов или операда маленьких интервалов (первоначально называвшаяся маленькими n -кубами PROP ) была определена Майклом Бордманом и Райнером Фогтом аналогичным образом в терминах конфигураций непересекающихся, выровненных по осям n -мерных гиперкубов (n- размерные интервалы ) внутри единичного гиперкуба . Позже это было обобщено Мэем. к маленьким выпуклым телам операд , а «диски» — это случай «фольклора», происходящего от «маленьких выпуклых тел».

Деревья с корнями

В теории графов корневые деревья образуют естественную операду. Здесь, $P(n)$ — множество всех корневых деревьев с n листьями, где листья пронумерованы от 1 до n. Группа $S_{n}$ работает с этим набором, переставляя метки листьев. Оперная композиция $T\circ (S_{1},\ldots ,S_{n})$ дается заменой i -го листа $T$ по корню i -го дерева $S_{i}$, для $i=1,\ldots ,n$, таким образом присоединяя n деревьев к $T$ и образуя большее дерево, корень которого считается таким же, как корень $T$ и чьи листья пронумерованы по порядку.

Швейцарско-сырная операда

Швейцарская сырная операда .

Операда « швейцарский сыр» — это двухцветная топологическая операда, определенная в терминах конфигураций непересекающихся n -мерных дисков внутри единичного n -полудиска и n -мерных полудисков, центрированных в основании единичного полудиска и находящихся внутри него. Оператическая композиция получается путем склеивания конфигураций «маленьких» дисков внутри единичного полудиска с «маленькими» дисками в другом единичном полудиске и конфигураций «маленьких» дисков и полудисков внутри единичного полудиска с другим единичным полудиском.

Швейцарскую сырную операду определил Александр А. Воронов . Его использовал Максим Концевич для формулировки сырной версии гипотезы Делиня о когомологиях Хохшильда. Kontsevich's conjecture was proven partly by Po Hu , Igor Kriz , and Alexander A. Voronov а затем полностью Джастином Томасом .

Ассоциативная операда

Другой класс примеров операд — это те, которые отражают структуры алгебраических структур, таких как ассоциативные алгебры, коммутативные алгебры и алгебры Ли. Каждый из них может быть представлен как конечно представленная операда, каждая из которых генерируется бинарными операциями.

Например, ассоциативная операда — это симметричная операда, созданная бинарной операцией. $\psi$, при условии лишь того, что

$\psi \circ (\psi ,1)=\psi \circ (1,\psi ).$

Это условие соответствует ассоциативности бинарной операции $\psi$; письмо $\psi (a,b)$ мультипликативно, вышеуказанное условие $(ab)c=a(bc)$. Эту ассоциативность операции не следует путать с ассоциативностью композиции , которая имеет место в любой операде; см. аксиому ассоциативности выше.

В ассоциативной операде каждый $P(n)$ задается симметрической группой $S_{n}$, на котором $S_{n}$ действует путем правильного умножения. Композитный $\sigma \circ (\tau _{1},\dots ,\tau _{n})$ переставляет свои входы в блоки в соответствии с $\sigma$, а внутри блоков согласно соответствующему $\tau _{i}$.

Алгебры над ассоциативной операдой представляют собой в точности полугруппы : множества, объединенные одной бинарной ассоциативной операцией. -линейные алгебры k над ассоциативной операдой являются в точности ассоциативными k- алгебрами .

Терминальная симметричная операда

Терминальная симметричная операда — это операда, которая имеет одну n -арную операцию для каждого n , причем каждая $S_{n}$ действует банально. Алгебры над этой операдой являются коммутативными полугруппами; k -алгебрами -линейные алгебры являются коммутативными ассоциативными k .

Операды из групп кос

Аналогично, существует не- $\Sigma$ операда, для которой каждая $P(n)$ задается группой кос Артина $B_{n}$. Более того, это не- $\Sigma$ операда имеет структуру косой операды, которая обобщает понятие операды от симметричных групп кос к группам кос.

Линейная алгебра

В линейной алгебре вещественные векторные пространства можно рассматривать как алгебры над операдой. $\mathbb {R} ^{\infty }$ всех линейных комбинаций . Эта операда определяется $\mathbb {R} ^{\infty }(n)=\mathbb {R} ^{n}$ для $n\in \mathbb {N}$, с очевидным действием $S_{n}$ перестановка компонентов и композиция ${\vec {x}}\circ ({\vec {y_{1}}},\ldots ,{\vec {y_{n}}})$ задается конкатенацией векторов $x^{(1)}{\vec {y_{1}}},\ldots ,x^{(n)}{\vec {y_{n}}}$, где ${\vec {x}}=(x^{(1)},\ldots ,x^{(n)})\in \mathbb {R} ^{n}$. Вектор ${\vec {x}}=(2,3,-5,0,\dots )$ например представляет собой операцию формирования линейной комбинации с коэффициентами 2,3,-5,0,...

Эта точка зрения формализует представление о том, что линейные комбинации являются наиболее общим видом операций над векторным пространством. Сказать, что векторное пространство является алгеброй над операдой линейных комбинаций, — это в точности утверждение, что все возможные алгебраические операции в векторном пространстве являются линейные комбинации. Основные операции сложения векторов и скалярного умножения являются порождающим набором операды всех линейных комбинаций, тогда как операда линейных комбинаций канонически кодирует все возможные операции в векторном пространстве.

Точно так же можно считать, что аффинные комбинации , конические комбинации и выпуклые комбинации соответствуют субоперадам, где члены вектора ${\vec {x}}$ если сумма равна 1, то все члены неотрицательны или оба соответственно. Графически это бесконечная аффинная гиперплоскость, бесконечный гипероктант и бесконечный симплекс. Это формализует то, что подразумевается под $\mathbb {R} ^{n}$ будучи или стандартный симплекс, являющийся модельным пространством, и такие наблюдения, как то, что каждый ограниченный выпуклый многогранник является образом симплекса. Здесь субоперады соответствуют более ограниченным операциям и, следовательно, более общим теориям.

Коммутативно-кольцевая операда и операда Ли

Операда коммутативных колец — это операда , алгебрами которой являются коммутативные кольца. Это определяется $P(n)=\mathbb {Z} [x_{1},\ldots ,x_{n}]$, с очевидным действием $S_{n}$ и операдическая композиция, задаваемая заменой переменных полиномами (с перенумерованными переменными). Можно определить аналогичную операду, алгебры которой являются ассоциативными коммутативными алгебрами над некоторым фиксированным базовым полем. Кошул -двойственной этой операде является операда Ли (алгебры которой являются алгебрами Ли), и наоборот.

Бесплатные операды

Типичные алгебраические конструкции (например, конструкции свободной алгебры) могут быть распространены на операды. Позволять $\mathbf {Set} ^{S_{n}}$ обозначают категорию, объектами которой являются множества, на которых группа $S_{n}$ действует. Тогда существует забывчивый функтор ${\mathsf {Oper}}\to \prod _{n\in \mathbb {N} }\mathbf {Set} ^{S_{n}}$, который просто забывает оперную композицию. Можно построить левый сопряженный $\Gamma :\prod _{n\in \mathbb {N} }\mathbf {Set} ^{S_{n}}\to {\mathsf {Oper}}$ этому забывчивому функтору (это обычное определение свободного функтора ). Учитывая набор операций E , $\Gamma (E)$ является свободной операдой на языке E.

Подобно группе или кольцу, свободная конструкция позволяет выразить операду через образующие и отношения. Путем свободного представления операды ${\mathcal {O}}$мы имеем в виду написание ${\mathcal {O}}$ как частное свободной операды ${\mathcal {F}}=\Gamma (E)$ где E описывает генераторы ${\mathcal {O}}$ и ядро ​​эпиморфизма ${\mathcal {F}}\to {\mathcal {O}}$ описывает отношения.

(симметричная) операда ${\mathcal {O}}=\{{\mathcal {O}}(n)\}$ называется квадратичным, если оно имеет свободное представление такое, что $E={\mathcal {O}}(2)$ является генератором, а отношение содержится в $\Gamma (E)(3)$.

Клоны

Клоны — это частный случай операд, которые также закрываются при совместном определении аргументов («повторное использование» некоторых данных). Клоны можно эквивалентно определить как операды, которые также являются миньонами (или клоноидами ).

Операды в теории гомотопий

В Сташефф (2004) Сташефф пишет:

Операды особенно важны и полезны в категориях с хорошим понятием «гомотопия», где они играют ключевую роль в организации иерархий высших гомотопий.

См. также

• ПРО (теория категорий)
• Алгебра над операдой
• Операда высшего порядка
• E∞-операда
• Псевдоалгебра
• Мультикатегория

Ссылки

• Том Ленстер (2004). Высшие операды, высшие категории . Издательство Кембриджского университета. arXiv : math/0305049 . Бибкод : 2004hohc.book.....L . ISBN  978-0-521-53215-0 .
• Мартин Маркл, Стив Шнайдер , Джим Сташефф (2002). Операды в алгебре, топологии и физике . Американское математическое общество. ISBN  978-0-8218-4362-8 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
• Маркл, Мартин (июнь 2006 г.). «Операды и реквизит». arXiv : math/0601129 .
• Сташефф, Джим (июнь – июль 2004 г.). «Что такое... операда?» (PDF) . Уведомления Американского математического общества . 51 (6): 630–631 . Проверено 17 января 2008 г.
• Лоде, Жан Луи ; Валлетт, Бруно (2012), Алгебраические операды (PDF) , Основы математических наук, том. 346, Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-3-642-30361-6
• Зинбиэль, Гийом В. (2012), «Энциклопедия типов алгебр 2010», в Бай, Ченгмин; Го, Ли; Лоде, Жан-Луи (ред.), Операды и универсальная алгебра , Серия Нанкай в чистом виде, Прикладная математика и теоретическая физика, том. 9, стр. 217–298, arXiv : 1101.0267 , Bibcode : 2011arXiv1101.0267Z , ISBN  9789814365116
• Фрессе, Бенуа (17 мая 2017 г.), Гомотопия операд и групп Гротендика-Тейхмюллера , Математические обзоры и монографии, Американское математическое общество , ISBN  978-1-4704-3480-9 , МР   3643404 , Збл   1373.55014
• Мигель А. Мендес (2015). Установить операды в комбинаторике и информатике . SpringerBriefs по математике. ISBN   978-3-319-11712-6 .
• Самуэле Жиродо (2018). Несимметричные операды в комбинаторике . Международное издательство Спрингер. ISBN   978-3-030-02073-6 .

Внешние ссылки

• операция в n лаборатории
• https://golem.ph.utexas.edu/category/2011/05/an_operadic_introduction_to_en.html