спираль

Правая спираль $(cos t, sin t, t)$ для $0 \leq t \leq 4 π$ со стрелками, показывающими направление увеличения $t.$

Спираль спирали ( / ˈ h iː l ɪ k s / ; мн. ) представляет собой форму , подобную цилиндрической пружине или резьбе машинного винта . Это тип гладкой пространственной кривой с касательными линиями, расположенными под постоянным углом к фиксированной оси. Спирали играют важную роль в биологии , поскольку молекула ДНК формируется в виде двух переплетенных спиралей , а многие белки имеют спиральные подструктуры, известные как альфа-спирали . Слово спираль происходит от греческого слова ἕλιξ , «скрученный, изогнутый». ^[1] «Заполненная» спираль – например, «спиральный» (винтовой) пандус – представляет собой поверхность, называемую геликоидом . ^[2]

Свойства и типы

Шаг спирали — это высота одного полного витка спирали , измеренная параллельно оси спирали.

состоит Двойная спираль из двух (обычно конгруэнтных ) спиралей с одной и той же осью, различающихся перемещением вдоль оси. ^[3]

Круговая спираль (т.е. спираль с постоянным радиусом) имеет постоянную кривизну ленты и постоянное кручение .

Коническая спираль , также известная как коническая спираль , может быть определена как спираль на конической поверхности, причем расстояние до вершины является экспоненциальной функцией угла, указывающего направление от оси.

Кривая называется общей спиралью или цилиндрической спиралью. ^[4] если его касательная составляет постоянный угол с фиксированной линией в пространстве. Кривая является общей спиралью тогда и только тогда, когда отношение кривизны к кручению постоянно. ^[5]

Кривая называется наклонной спиралью , если ее главная нормаль образует постоянный угол с фиксированной линией в пространстве. ^[6] Его можно построить, применив преобразование к движущейся системе отсчета общей спирали. ^[7]

Более общие спиралевидные пространственные кривые можно найти в разделе « Пространственная спираль» ; например, сферическая спираль .

Рукава

Спирали могут быть как правосторонними, так и левосторонними. При луче зрения вдоль оси спирали, если завинчивающее движение по часовой стрелке отодвигает спираль от наблюдателя, то это называется правосторонней спиралью; если к наблюдателю, то это левая спираль. Направленность (или хиральность ) — это свойство спирали, а не перспективы: правую спираль нельзя повернуть так, чтобы она выглядела как левая, если ее не посмотреть в зеркало, и наоборот.

Математическое описание

В математике спираль — это кривая в трехмерном пространстве . Следующая параметризация в декартовых координатах определяет конкретную спираль; ^[8] возможно, самое простое уравнение для одного:

{\begin{aligned}x(t)&=\cos(t),\\y(t)&=\sin(t),\\z(t)&=t.\end{aligned}}

По мере увеличения параметра $t$ точка $(x (t), y (t), z (t))$ описывает правую спираль с шагом $2 π$ (или наклоном 1) и радиусом 1 вокруг $оси z$ , в правая система координат.

В цилиндрических координатах $(r, θ, h)$ одна и та же спираль параметризуется следующим образом:

{\begin{aligned}r(t)&=1,\\\theta (t)&=t,\\h(t)&=t.\end{aligned}}

Круговая спираль радиуса $a$ и наклона $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ a / b ⁠$ (или шаг $2 πb$ ) описывается следующей параметризацией:

{\begin{aligned}x(t)&=a\cos(t),\\y(t)&=a\sin(t),\\z(t)&=bt.\end{aligned}}

Другой способ математического построения спирали — построить график комплексной функции $e xi$ как функция действительного числа $x$ (см. формулу Эйлера ).Значение $x$ , а также действительная и мнимая части значения функции придают этому графику три действительных измерения.

За исключением вращений , перемещений и изменений масштаба, все правые спирали эквивалентны спирали, определенной выше. Эквивалентную левую спираль можно построить несколькими способами, самый простой из которых — отрицание любого из $компонентов x$ , $y$ или $z$ .

Длина дуги, кривизна и кручение

Круговая спираль радиуса $a$ и наклона $⁠ a / b ⁠$ (или шаг $2 πb$ ), выраженный в декартовых координатах как параметрическое уравнение

t\mapsto (a\cos t,a\sin t,bt),t\in [0,T]

имеет дуги длину

A=T\cdot {\sqrt {a^{2}+b^{2}}},

кривизна

{\frac {|a|}{a^{2}+b^{2}}},

и перекручивание

{\frac {b}{a^{2}+b^{2}}}.

Спираль имеет постоянную ненулевую кривизну и кручение.

Спираль — это векторная функция

${\begin{aligned}\mathbf {r} &=a\cos t\mathbf {i} +a\sin t\mathbf {j} +bt\mathbf {k} \\[6px]\mathbf {v} &=-a\sin t\mathbf {i} +a\cos t\mathbf {j} +b\mathbf {k} \\[6px]\mathbf {a} &=-a\cos t\mathbf {i} -a\sin t\mathbf {j} +0\mathbf {k} \\[6px]|\mathbf {v} |&={\sqrt {(-a\sin t)^{2}+(a\cos t)^{2}+b^{2}}}={\sqrt {a^{2}+b^{2}}}\\[6px]|\mathbf {a} |&={\sqrt {(-a\sin t)^{2}+(a\cos t)^{2}}}=a\\[6px]s(t)&=\int _{0}^{t}{\sqrt {a^{2}+b^{2}}}d\tau ={\sqrt {a^{2}+b^{2}}}t\end{aligned}}$

Таким образом, спираль можно перепараметризовать как функцию $s$ , которая должна иметь единичную скорость:

$\mathbf {r} (s)=a\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} +a\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +{\frac {bs}{\sqrt {a^{2}+b^{2}}}}\mathbf {k}$

Единичный касательный вектор

${\frac {d\mathbf {r} }{ds}}=\mathbf {T} ={\frac {-a}{\sqrt {a^{2}+b^{2}}}}\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} +{\frac {a}{\sqrt {a^{2}+b^{2}}}}\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +{\frac {b}{\sqrt {a^{2}+b^{2}}}}\mathbf {k}$

Нормальный вектор

${\frac {d\mathbf {T} }{ds}}=\kappa \mathbf {N} ={\frac {-a}{a^{2}+b^{2}}}\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} +{\frac {-a}{a^{2}+b^{2}}}\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +0\mathbf {k}$

Его кривизна

$\kappa =\left|{\frac {d\mathbf {T} }{ds}}\right|={\frac {|a|}{a^{2}+b^{2}}}$ .

Единичный вектор нормали

$\mathbf {N} =-\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} -\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +0\mathbf {k}$

Бинормальный вектор

${\begin{aligned}\mathbf {B} =\mathbf {T} \times \mathbf {N} &={\frac {1}{\sqrt {a^{2}+b^{2}}}}\left(b\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} -b\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +a\mathbf {k} \right)\\[12px]{\frac {d\mathbf {B} }{ds}}&={\frac {1}{a^{2}+b^{2}}}\left(b\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} +b\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +0\mathbf {k} \right)\end{aligned}}$

Его кручение $\tau =\left|{\frac {d\mathbf {B} }{ds}}\right|={\frac {b}{a^{2}+b^{2}}}.$

Примеры

Примером двойной спирали в молекулярной биологии является двойная спираль нуклеиновой кислоты .

Примером конической спирали являются американские горки «Штопор» в парке развлечений Сидар-Пойнт .

Некоторые кривые, встречающиеся в природе, состоят из множества спиралей разной направленности, соединенных между собой переходами, известными как перверсии усиков .

Большинство аппаратных винтовых резьб имеют правую спираль. Альфа-спираль в биологии, а также формы ДНК A и B также являются правосторонними спиралями. ДНК Z-форма является левосторонней.

В музыке часто моделируется с помощью спиралей или двойных спиралей , пространство высоты тона чаще всего выходящих за пределы круга, такого как круг квинт , чтобы представить октавную эквивалентность .

В авиации геометрический шаг — это расстояние, на которое элемент винта самолета продвинулся бы за один оборот, если бы он двигался по спирали, имеющей угол, равный углу между хордой элемента и плоскостью, перпендикулярной оси винта; см. также: угол тангажа (авиационный) .

Кристаллическая структура свернутой молекулярной спирали, о которой сообщили Лен и др. ^[9]
Естественная левая спираль, образованная вьющимся растением.
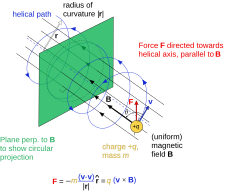
Заряженная частица в однородном магнитном поле движется по винтовой траектории.
Винтовая пружина

См. также

Ссылки

^ ἕλιξ. Архивировано 16 октября 2012 г. в Wayback Machine , Генри Джордж Лидделл, Роберт Скотт, Греко-английский лексикон , о Персее.
^ Вайсштейн, Эрик В. «Геликоид» . Математический мир .
^ « Двойная спираль, архивировано 30 апреля 2008 г. в Wayback Machine », Шандор Кабай, Демонстрационный проект Wolfram .
^ О'Нил, Б. Элементарная дифференциальная геометрия, 1961, стр. 72.
^ О'Нил, Б. Элементарная дифференциальная геометрия, 1961, стр. 74.
^ Изумия, С. и Такеучи, Н. (2004) Новые специальные кривые и развертывающиеся поверхности. Turk J Math. Архивировано 4 марта 2016 г. в Wayback Machine , 28:153–163.
^ Меннингер, Т. (2013), Явная параметризация аппарата Френе наклонной спирали . arXiv:1302.3175. Архивировано 5 февраля 2018 г. в Wayback Machine .
^ Вайсштейн, Эрик В. «Спираль» . Математический мир .
^ Шмитт, Ж.-Л.; Стадлер, А.-М.; Кирицакас, Н.; Лен, Ж.-М. (2003). «Молекулярные нити, закодированные спиральностью: эффективный доступ по гидразонному маршруту и структурные особенности». Helvetica Chimica Acta . 86 : 1598–1624. дои : 10.1002/hlca.200390137 .

[1] ἕλιξ. Архивировано 16 октября 2012 г. в Wayback Machine , Генри Джордж Лидделл, Роберт Скотт, Греко-английский лексикон , о Персее.

[2] Вайсштейн, Эрик В. «Геликоид» . Математический мир .

[3] « Двойная спираль, архивировано 30 апреля 2008 г. в Wayback Machine », Шандор Кабай, Демонстрационный проект Wolfram .

[4] О'Нил, Б. Элементарная дифференциальная геометрия, 1961, стр. 72.

[5] О'Нил, Б. Элементарная дифференциальная геометрия, 1961, стр. 74.

[6] Изумия, С. и Такеучи, Н. (2004) Новые специальные кривые и развертывающиеся поверхности. Turk J Math. Архивировано 4 марта 2016 г. в Wayback Machine , 28:153–163.

[7] Меннингер, Т. (2013), Явная параметризация аппарата Френе наклонной спирали . arXiv:1302.3175. Архивировано 5 февраля 2018 г. в Wayback Machine .

[8] Вайсштейн, Эрик В. «Спираль» . Математический мир .

[9] Шмитт, Ж.-Л.; Стадлер, А.-М.; Кирицакас, Н.; Лен, Ж.-М. (2003). «Молекулярные нити, закодированные спиральностью: эффективный доступ по гидразонному маршруту и структурные особенности». Helvetica Chimica Acta . 86 : 1598–1624. дои : 10.1002/hlca.200390137 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]