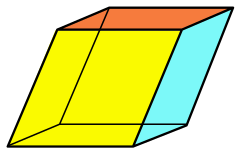
Ромбоэдр

Ромбоэдр
Тип	призма
Лица	6 ромбов
Края	12
Вершины	8
Группа симметрии	С я , [2 + ,2 + ], (×), порядок 2
Характеристики	выпуклый , равносторонний , зоноэдр , параллелоэдр

В геометрии ромбоэдр ) (также называемый ромб-шестигранником или, неточно, ромб ) — частный случай параллелепипеда , у которого все шесть граней — конгруэнтные ромбы . Его можно использовать для определения ромбоэдрической решетчатой ​​системы , сот с ромбоэдрическими ячейками. У ромбоэдра есть две противоположные вершины, у которых все углы граней равны; у вытянутого ромбоэдра этот общий угол острый, а у сплюснутого ромбоэдра - тупой угол в этих вершинах. Куб стороны — это частный случай ромбоэдра, у которого все квадратные .

Особые случаи

Общий угол между двумя вершинами здесь определяется как $\theta$.Существует две основные формы ромбоэдра: сплюснутая (сплющенная) и вытянутая (вытянутая).

Сплющенный ромбоэдр	Вытянутый ромбоэдр

В сжатом случае $\theta >90^{\circ }$ и в расширенном случае $\theta <90^{\circ }$. Для $\theta =90^{\circ }$ фигура представляет собой куб.

Определенные пропорции ромбов приводят к некоторым хорошо известным частным случаям. Обычно они встречаются как в вытянутой, так и в сплюснутой формах.

Форма	Куб	√2 Ромбоэдр	Золотой ромбоэдр
Угол ограничения	$\theta =90^{\circ }$
Соотношение диагоналей	1	√2	Золотое сечение
возникновение	Обычный твердый	Рассечение ромбододекаэдра	Рассечение ромботриаконтаэдра

Твердая геометрия

Для единичного (т. е. с длиной стороны 1) ромбоэдра с ромбическим острым углом $\theta ~$, с одной вершиной в начале координат (0, 0, 0) и с одним ребром, лежащим вдоль оси x, три порождающих вектора:

и ₁ : ${\biggl (}1,0,0{\biggr )},$

е2 : ${\biggl (}\cos \theta ,\sin \theta ,0{\biggr )},$

е ₃ : ${\biggl (}\cos \theta ,{\cos \theta -\cos ^{2}\theta \over \sin \theta },{{\sqrt {1-3\cos ^{2}\theta +2\cos ^{3}\theta }} \over \sin \theta }{\biggr )}.$

Остальные координаты можно получить сложением векторов. трех e1 _​ + e2 _​ , e1 _e3 + из _​ , e2 _e3 + ​ _​ и e1 ₊ . e2 _e3 + : _{векторов} направления

Объем $V$ ромбоэдра по длине его стороны $a$ и его ромбический острый угол $\theta ~$, является упрощением объема параллелепипеда и определяется выражением

$V=a^{3}(1-\cos \theta ){\sqrt {1+2\cos \theta }}=a^{3}{\sqrt {(1-\cos \theta )^{2}(1+2\cos \theta )}}=a^{3}{\sqrt {1-3\cos ^{2}\theta +2\cos ^{3}\theta }}~.$

Мы можем выразить объем $V$ другой способ:

$V=2{\sqrt {3}}~a^{3}\sin ^{2}\left({\frac {\theta }{2}}\right){\sqrt {1-{\frac {4}{3}}\sin ^{2}\left({\frac {\theta }{2}}\right)}}~.$

Поскольку площадь (ромбического) основания определяется выражением $a^{2}\sin \theta ~$, а поскольку высота ромбоэдра определяется его объемом, деленным на площадь его основания, то высота $h$ ромбоэдра по длине его стороны $a$ и его ромбический острый угол $\theta$ дается

$h=a~{(1-\cos \theta ){\sqrt {1+2\cos \theta }} \over \sin \theta }=a~{{\sqrt {1-3\cos ^{2}\theta +2\cos ^{3}\theta }} \over \sin \theta }~.$

Примечание:

$h=a~z$₃ , где $z$₃ — третья координата e ₃ .

Диагональ тела между остроугольными вершинами самая длинная. Благодаря вращательной симметрии относительно этой диагонали все остальные три диагонали тела между тремя парами противоположных тупоугольных вершин имеют одинаковую длину.

Связь с ортоцентрическими тетраэдрами

Четыре точки, образующие несмежные вершины ромбоэдра, обязательно образуют четыре вершины ортоцентрического тетраэдра , и таким способом можно образовать все ортоцентрические тетраэдры.

Ромбоэдрическая решетка

Основная статья: Ромбоэдрическая решетка

Система ромбоэдрической решетки имеет ромбоэдрические ячейки с 6 конгруэнтными ромбическими гранями, образующими тригональный трапецоэдр. :

См. также

• Списки фигур

Внешние ссылки

• Вайсштейн, Эрик В. «Ромбоэдр» . Математический мир .
• Калькулятор объема https://rechneronline.de/pi/rhombohedron.php