Гармонический

Эта статья о компонентах периодических сигналов. Чтобы узнать о других значениях, см. Гармоника (значения) .

Узлы . колеблющейся струны являются гармониками

Два разных обозначения натуральных гармоник на виолончели. Сначала как звучит (чаще), затем как на ощупь (легче читается с листа).

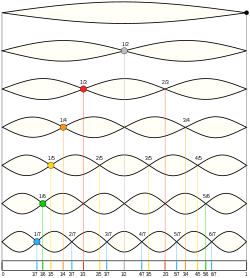
В физике , акустике и телекоммуникациях гармоника с — это синусоидальная волна частотой , которая является целым положительным кратным основной частоты сигнала периодического . Основная частота также называется 1-й гармоникой ; остальные гармоники известны как высшие гармоники . Поскольку все гармоники являются периодическими на основной частоте, сумма гармоник также является периодической на этой частоте. Совокупность гармоник образует гармонический ряд .

Этот термин используется в различных дисциплинах, включая музыку, физику, акустику , электронную передачу энергии, радиотехнологии и другие области. Например, если основная частота составляет 50 Гц (обычная частота источника переменного тока ), частоты первых трех высших гармоник составляют 100 Гц (2-я гармоника), 150 Гц (3-я гармоника), 200 Гц (4-я гармоника) и любое дополнение. волн с этими частотами является периодическим с частотой 50 Гц.

И н ^й Характерный режим при n > 1 будет иметь узлы, которые не колеблются. Например, 3-я характеристическая мода будет иметь узлы в точках ${\tfrac {1}{3}}$Земля ​ ${\tfrac {2}{3}}$L , где L — длина строки. Фактически, каждое n ^й характерный режим, для n, не кратного 3, не будет иметь узлов в этих точках. Эти другие характерные моды будут вибрировать в положениях ${\tfrac {1}{3}}$Земля ​ ${\tfrac {2}{3}}$Л. ​Если игрок осторожно коснется одной из этих позиций, то остальные характерные режимы будут подавлены. Тональные гармоники этих других характеристических мод также будут подавлены. Следовательно, тональные гармоники из n ^й характерные моды, где n кратно 3, станут относительно более заметными.

В музыке гармоники используются на струнных и духовых инструментах как способ создания звука на инструменте, особенно для воспроизведения более высоких нот, а с помощью струнных - для получения нот, которые имеют уникальное качество звука или «цвет тона». На струнных смычковые гармоники имеют «стеклянный», чистый тон. На струнных инструментах гармоники воспроизводятся путем прикосновения (но не полного нажатия) к определенной точке струны во время звучания струны (щипка, смычка и т. д.); это позволяет звучать гармонике, высота которой всегда выше основной частоты струны.

Терминология

Гармоники можно называть «обертонами», «частичными» или «верхними частичными», а в некоторых музыкальных контекстах термины «гармоника», «обертон» и «частичный» используются довольно взаимозаменяемо. Но точнее, термин «гармоника» включает в себя все звуки гармонического ряда (включая основную частоту), тогда как термин «обертон» включает только звуки выше основной частоты.

Характеристики

Свистящий, свистящий тональный характер отличает все гармоники, как естественные, так и искусственные, от твердо остановившихся интервалов; поэтому их применение в связи с последними всегда должно быть тщательно продумано.

— Рихард Шольц ( ок. 1888-1912 )

Большинство акустических инструментов издают сложные тоны, содержащие множество отдельных частей (простые составляющие тонов или синусоидальные волны), но нетренированное человеческое ухо обычно не воспринимает эти частичные звуки как отдельные явления. Скорее, музыкальная нота воспринимается как один звук, качество или тембр этого звука являются результатом относительной силы отдельных частей. Многие акустические осцилляторы , такие как человеческий голос или смычковая струна скрипки , производят сложные тона, которые являются более или менее периодическими и, таким образом, состоят из частичных звуков, которые почти соответствуют целым кратным основной частоте и, следовательно, напоминают идеальные гармоники и являются не совсем точно » (хотя называть частичную гармоникой для удобства называются «гармоническими частичными» или просто « гармониками , первая из которых является фактической, а вторая — теоретической).

Генераторы, которые производят гармонические частичные звуки, ведут себя как одномерные резонаторы и часто бывают длинными и тонкими, например, гитарная струна или столб воздуха, открытый с обоих концов (как в случае с металлической современной оркестровой поперечной флейтой ). Духовые инструменты, столб воздуха у которых открыт только с одного конца, например трубы и кларнеты , также производят частичные звуки, напоминающие гармоники. Однако они производят только частичные, соответствующие нечетным гармоникам — по крайней мере, теоретически. При практическом использовании ни один реальный акустический инструмент не ведет себя так идеально, как предсказывают упрощенные физические модели; например, инструменты, сделанные из нелинейно- упругого дерева, а не из металла, или нанизанные на жилы вместо латунных или стальных струн , как правило, имеют не совсем целые частичные числа.

Частичные частицы, частоты которых не кратны основной частоте, называются негармоничными частичными частотами . Некоторые акустические инструменты излучают смесь гармонических и негармонических частей, но все же производят на ухо определенный основной тон, например фортепиано , пиццикато с перещипыванием струн , вибрафоны, маримбы и некоторые чисто звучащие колокольчики или колокольчики. Антикварные поющие чаши известны тем, что создают несколько гармонических частей или мультифонику . Другие осцилляторы, такие как тарелки , пластики барабанов и большинство ударных инструментов, естественным образом производят множество негармонических партий и не подразумевают какой-либо определенной высоты тона, и поэтому не могут использоваться мелодически или гармонически так же, как другие инструменты.

Основываясь на Сетаресе (2004), Динамическая тональность вводит понятие псевдогармонических партий, в которых частота каждой партии выравнивается так, чтобы соответствовать высоте соответствующей ноты в псевдоточной настройке, тем самым максимизируя созвучие этого псевдогармонического тембра с нотами этого псевдогармонического тембра. -просто тюнинг.

Партии, обертоны и гармоники

Обертон – это любая частичка выше самой низкой части сложного тона. Относительная сила и частотные соотношения составляющих определяют тембр инструмента. Сходство между терминами «обертон» и «частичный» иногда приводит к тому, что они широко используются как взаимозаменяемые в музыкальном контексте, но они считаются по-разному, что приводит к некоторой возможной путанице. В особом случае инструментальных тембров, чьи частичные составляющие близко соответствуют гармоническому ряду (например, у большинства струнных и духовых инструментов), а не являются негармоничными частичными звуками (например, у большинства ударных инструментов), составляющие частичные части также удобно называть «гармониками». ", но это не совсем правильно, поскольку гармоники нумеруются одинаково, даже если они отсутствуют, тогда как частичные и обертоны учитываются только при их наличии. Эта диаграмма демонстрирует, как подсчитываются три типа имен (частичные, обертоновые и гармонические) (при условии присутствия гармоник):

Частота	Заказ ( н )	Имя 1	Имя 2	Имя 3	стоячей волны Представление	продольных волн Представление
1 × f = 0 440 Гц	п = 1	1-я частичная	основной тон	1-я гармоника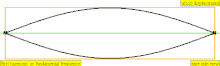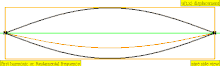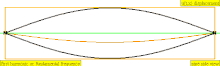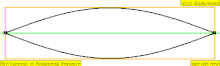
2 × f = 0880 Гц	п = 2	2-я частичная	1-й обертон	2-я гармоника
3 × f = 1320 Гц	п = 3	3-я частичная	2-й обертон	3-я гармоника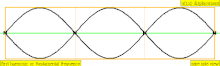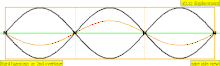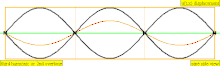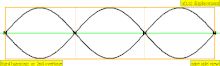
4 × f = 1760 Гц	п = 4	4-я частичная	3-й обертон	4-я гармоника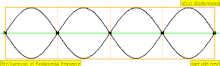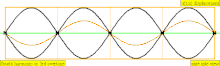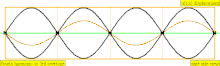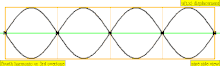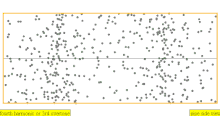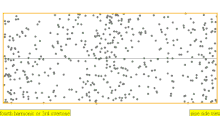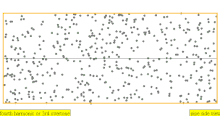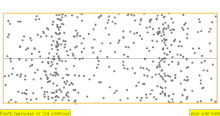

Во многих музыкальных инструментах можно играть верхние гармоники без присутствия основной ноты. В простом случае (например, блокфлейта ) это приводит к повышению высоты ноты на октаву , но в более сложных случаях получается множество других вариаций высоты звука. В некоторых случаях это также меняет тембр ноты. Это часть обычного метода получения более высоких нот в духовых инструментах , где это называется передутием . игры Расширенная техника на мультифонике также производит гармоники. На струнных инструментах можно воспроизводить очень чистые звучащие ноты, называемые струнными музыкантами гармониками или флажолетами , которые имеют жуткое качество, а также имеют высокую высоту звука. Гармоники можно использовать для проверки унисон настройки струн, которые не настроены в , в унисон. Например, легкое нажатие на узел, расположенный посередине самой высокой струны виолончели, дает ту же высоту звука, что и легкое нажатие на узел. ⁠ 1/3 струне ⁠ . пути вниз по второй по высоте Чтобы узнать о человеческом голосе, см. Обертоновое пение , в котором используются гармоники.

Хотя это правда, что периодические тоны, создаваемые электроникой (например, прямоугольные волны или другие несинусоидальные волны), имеют «гармоники», кратные основной частоте, не все практические инструменты обладают этой характеристикой. Например, высшие «гармоники» фортепианных нот не являются истинными гармониками, а являются «обертонами» и могут быть очень резкими, то есть более высокой частотой, чем дается чистым гармоническим рядом . Это особенно верно для других инструментов, кроме струнных , медных или деревянных духовых инструментов . Примерами этих «других» инструментов являются ксилофоны, барабаны, колокольчики, колокольчики и т. д.; не все их обертоновые частоты составляют простое целое числовое отношение к основной частоте. ( Основная частота является обратной величиной самого длительного периода времени совокупности вибраций в каком-то одном периодическом явлении. )

На струнных инструментах

Игра гармоники на струне

Основная статья: Струнная гармоника

Гармоники могут быть созданы по отдельности [на струнных инструментах] (1) путем изменения точки контакта со смычком или (2) путем легкого надавливания струны в узлах или деления ее кратных частей ( ${\tfrac {\ 1\ }{2}}$, ${\tfrac {\ 1\ }{3}}$, ${\tfrac {\ 1\ }{4}}$, и т. д.). (1) В первом случае, продвигая смычок от обычного места, где издается основная нота, к мосту, можно последовательно воспроизвести всю гамму гармоник на старом и очень резонансном инструменте. Применение этого средства производит эффект, называемый « sul ponticello ». (2) Более полезно создавать гармоники легким нажатием пальца на открытую струну. Когда они производятся легким нажатием на различные узлы открытых струн, они называются «естественными гармониками». ... Скрипачи хорошо знают, что чем длиннее струна по отношению к ее толщине, тем большее количество верхних гармоник она может воспроизвести.

- Словарь музыки и музыкантов Гроува (1879 г.)

В следующей таблице показаны точки остановки струнного инструмента, в которых легкое прикосновение к струне переводит ее в гармонический режим при вибрации. Струнные гармоники (тоны флажолета) описываются как имеющие «флейтоподобное, серебристое качество», которое может быть очень эффективным в качестве особого цвета или цвета тона ( тембра ) при использовании и прослушивании в оркестровке . Необычно встретить естественные гармоники выше пятой части на любом струнном инструменте, кроме контрабаса, из-за его гораздо более длинных струн.

Гармонический	Стоп-нота	Нота прозвучала (относительно открытая строка)	Звуковая частота ( Гц )	центов выше основной (смещение на октаву)	Аудио (сдвинута октава)
1	фундаментальный , идеальный унисон	П1	600	0.0
2	первая идеальная октава	Р8	1,200	0.0
3	идеальная пятая часть	П8 + П5	1,800	702.0
4	удвоенная идеальная октава	2·П8	2,400	0.0
5	просто мажорная треть , главная треть	2·П8+М3	3,000	386.3
6	идеальная пятая часть	2·П8 + П5	3,600	702.0
7	гармоническая седьмая , септимальная минорная седьмая («потерянный аккорд»)	2·П8 + м7↓	4,200	968.8
8	третья идеальная октава	3·П8	4,800	0.0
9	Пифагорейская мажорная секунда девятая гармония	3·П8 + М2	5,400	203.9
10	просто главная треть	3·П8+М3	6,000	386.3
11	меньший недесятичный тритон , недесятичная полурасширенная четвертая	3·P8 + a4	6,600	551.3
12	идеальная пятая часть	3·П8 + П5	7,200	702.0
13	трехзначный нейтральный шестой	3·П8 + n6 ↓	7,800	840.5
14	гармоническая седьмая , септимальная минорная седьмая («потерянный аккорд»)	3·П8 + м7⤈	8,400	968.8
15	просто мажорный седьмой	3 Р8 + М7	9,000	1,088.3
16	четвертая идеальная октава	4·П8	9,600	0.0
17	семидесятичный полутон	4·P8 + м2⇟	10,200	105.0
18	Пифагорейская мажорная секунда	4·П8 + М2	10,800	203.9
19	нанодесятичная малая треть	4·П8+м3	11,400	297.5
20	просто главная треть	4·П8+М3	12,000	386.3

Искусственные гармоники

Иногда в партитуре требуется искусственная гармоника , создаваемая игрой обертона на уже остановленной струне. В качестве техники исполнения это достигается использованием двух пальцев на грифе: первый укорачивает струну до желаемой основной тональности, а второй касается узла, соответствующего соответствующей гармонике.

Другая информация

Гармоники могут либо использоваться, либо рассматриваться как основа интонационных систем. Композитор Арнольд Дрейблатт способен добиться различных гармоник на одной струне своего модифицированного контрабаса , слегка изменив свою уникальную технику смычка на полпути между ударом по струнам и смычком. Композитор Лоуренс Болл использует гармоники для создания музыки в электронном виде.

См. также

• Аристоксен
• Электронный тюнер
• Форманта
• ряд Фурье
• Гитарная гармоника
• Гармонический анализ
• Гармоники (электрическая мощность)
• Гармоническая генерация
• Гармонический осциллятор
• Гармония
• Чистый тон
• Пифагорова настройка
• Шкала гармоник
• Сферические гармоники
• Растянутая октава
• Субгармоника
• Ксенгармоническая музыка

Внешние ссылки

• Фейнмановские лекции по физике: гармоники
• Гармоники, частичные и обертоны основной частоты
• Чисхолм, Хью , изд. (1911). «Гармоничный» . Британская энциклопедия (11-е изд.). Издательство Кембриджского университета.
• Гармоники
• Слушайте и смотрите гармоники на фортепиано