Планирование движения

Планирование движения , также планирование пути (также известное как проблема навигации или проблема перемещения пианино ) — это вычислительная задача , позволяющая найти последовательность допустимых конфигураций, которая перемещает объект от источника к месту назначения. Этот термин используется в вычислительной геометрии , компьютерной анимации , робототехнике и компьютерных играх .

Например, рассмотрим навигацию мобильного робота внутри здания к удаленной путевой точке. Он должен выполнить эту задачу, избегая стен и не падая с лестницы. Алгоритм планирования движения будет принимать описание этих задач в качестве входных данных и генерировать команды скорости и поворота, отправляемые на колеса робота. Алгоритмы планирования движения могут быть ориентированы на роботов с большим количеством соединений (например, промышленные манипуляторы), более сложными задачами (например, манипулирование объектами), различными ограничениями (например, автомобиль, который может двигаться только вперед) и неопределенностью (например, несовершенные модели окружающая среда или робот).

Планирование движения имеет несколько приложений в робототехнике, таких как автономность , автоматизация и проектирование роботов в программном обеспечении САПР , а также приложения в других областях, таких как анимация цифровых персонажей , видеоигры , архитектурное проектирование , роботизированная хирургия и исследование биологических молекул .

Концепции

Пример рабочего пространства

Конфигурационное пространство точечного робота. Белый = C _{бесплатно} , серый = C _obs .

Конфигурационное пространство для прямоугольного робота-переводчика (на фото красным). Белый = C _free , серый = C _obs , где тёмно-серый = объекты, светло-серый = конфигурации, в которых робот коснётся объекта или покинет рабочую область.

Пример допустимого пути

Пример неверного пути

Пример дорожной карты

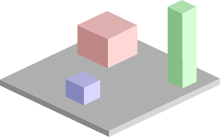
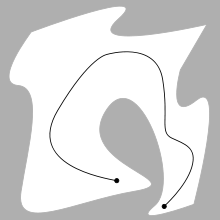
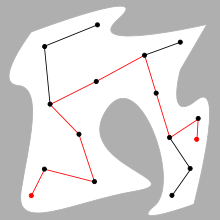
Основная задача планирования движения состоит в вычислении непрерывного пути, который соединяет начальную конфигурацию S и целевую конфигурацию G, избегая при этом столкновений с известными препятствиями. Геометрия робота и препятствий описывается в 2D или 3D рабочем пространстве , а движение представляется как путь в (возможно, многомерном) конфигурационном пространстве .

Конфигурационное пространство

Конфигурация описывает положение робота, а пространство конфигурации C представляет собой набор всех возможных конфигураций. Например:

• Если робот представляет собой одну точку (нулевого размера), перемещающуюся в двумерной плоскости (рабочее пространство), C является плоскостью, и конфигурация может быть представлена ​​с использованием двух параметров (x, y).
• Если робот представляет собой двумерную фигуру, которая может перемещаться и вращаться, рабочее пространство по-прежнему остается двухмерным. Однако C — специальная евклидова группа SE (2) = R ² $\times$ SO (2) (где SO (2) — специальная ортогональная группа двумерных вращений), а конфигурацию можно представить с помощью трех параметров (x, y, θ).
• Если робот представляет собой твердую трехмерную форму, которая может перемещаться и вращаться, рабочее пространство является трехмерным, но C — это специальная евклидова группа SE (3) = R. ³ $\times$ SO (3), а конфигурация требует 6 параметров: (x, y, z) для перемещения и углы Эйлера (α, β, γ).
• Если робот представляет собой манипулятор с фиксированной базой и N вращающимися соединениями (и без замкнутых контуров), C является N-мерным.

Свободное место

Набор конфигураций, позволяющий избежать столкновения с препятствиями, называется свободным пространством C _free . Дополнение C, _{свободное} в C, называется препятствием или запрещенной областью.

Часто бывает непомерно сложно явно вычислить форму C _free . Однако проверка того, является ли данная конфигурация _{свободной} от C , эффективна. Во-первых, прямая кинематика определяет положение геометрии робота, а обнаружение столкновений проверяет, сталкивается ли геометрия робота с геометрией окружающей среды.

Целевое пространство

Целевое пространство — это подпространство свободного пространства, которое обозначает, куда мы хотим, чтобы робот переместился. При глобальном планировании движения целевое пространство наблюдается с помощью датчиков робота. Однако при планировании локального движения в некоторых состояниях робот не может наблюдать целевое пространство. Для решения этой задачи робот проходит несколько виртуальных целевых пространств, каждое из которых находится в пределах наблюдаемой области (вокруг робота). Виртуальное целевое пространство называется подцелью.

Пространство препятствий

Пространство препятствий — это пространство, куда робот не может переместиться. Пространство препятствий не является противоположностью свободного пространства.

Алгоритмы

Задачи малой размерности можно решать с помощью сеточных алгоритмов, которые накладывают сетку поверх конфигурационного пространства, или геометрических алгоритмов, вычисляющих форму и связность C _free .

Точное планирование движения для многомерных систем при сложных ограничениях вычислительно сложно . Алгоритмы потенциального поля эффективны, но становятся жертвой локальных минимумов (исключением являются гармонические потенциальные поля). Алгоритмы, основанные на выборке, избегают проблемы локальных минимумов и решают многие проблемы довольно быстро. Они не могут определить, что пути не существует, но у них есть вероятность неудачи, которая уменьшается до нуля по мере того, как тратится больше времени.

Алгоритмы, основанные на выборке, в настоящее время считаются самыми современными для планирования движения в многомерных пространствах и применяются к задачам, имеющим десятки или даже сотни измерений (роботы-манипуляторы, биологические молекулы, анимированные цифровые персонажи и ноги). роботы ).

Поиск по сетке

Подходы, основанные на сетке, накладывают сетку на пространство конфигурации и предполагают, что каждая конфигурация идентифицируется точкой сетки. В каждой точке сетки роботу разрешено перемещаться к соседним точкам сетки, пока линия между ними полностью содержится в пределах C _free (это проверяется с помощью обнаружения столкновений). Это дискретизирует набор действий, и алгоритмы поиска (например, A* ) используются для поиска пути от начала до цели.

Эти подходы требуют установки разрешения сетки. Поиск выполняется быстрее с более грубой сеткой, но алгоритм не сможет найти пути через узкие участки C _free . Более того, количество точек на сетке растет экспоненциально в размерности конфигурационного пространства, что делает их непригодными для задач большой размерности.

Традиционные подходы, основанные на сетке, создают пути, изменения курса которых ограничены кратностью заданного базового угла, что часто приводит к неоптимальным путям. Подходы к планированию пути под любым углом находят более короткие пути, распространяя информацию вдоль краев сетки (для быстрого поиска), не ограничивая их пути краями сетки (для поиска коротких путей).

Подходы, основанные на сетке, часто требуют многократного поиска, например, когда знания робота о пространстве конфигурации изменяются или само пространство конфигурации меняется во время следования по пути. Алгоритмы инкрементного эвристического поиска быстро перепланируются, используя опыт предыдущих аналогичных задач планирования пути, чтобы ускорить поиск текущей.

Интервальный поиск

Эти подходы аналогичны подходам поиска на основе сетки, за исключением того, что они вместо сетки создают покрытие, полностью покрывающее пространство конфигурации. Тротуар разбивается на два подмощения X ⁻ ,Х ⁺ сделано из коробок таких, что X ⁻ ⊂ C _{свободен} ⊂ X ⁺ . Характеризация C _free позволяет решить проблему инверсии множеств . Таким образом, интервальный анализ можно использовать, когда C _free не может быть описан линейными неравенствами, чтобы иметь гарантированную вложенность.

Таким образом, роботу разрешено свободно перемещаться в X. ⁻ , и не может выйти за пределы X ⁺ . Для обоих подмощений строится граф соседей, и пути можно найти с помощью таких алгоритмов, как Дейкстра или A* . Когда путь возможен в X ⁻ , это также возможно в C _{бесплатно} . Когда в X нет пути ⁺ от одной начальной конфигурации до цели, у нас есть гарантия, что в C _free не существует допустимого пути . Что касается сеточного подхода, то интервальный подход не подходит для задач большой размерности из-за того, что количество генерируемых блоков растет экспоненциально по отношению к размерности конфигурационного пространства.

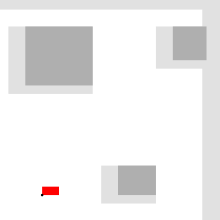
Иллюстрацией служат три фигуры справа, где крючок с двумя степенями свободы должен двигаться слева направо, избегая двух горизонтальных маленьких сегментов.

Движение от начальной конфигурации (синего цвета) к конечной конфигурации крючка, обходя два препятствия (красные сегменты). Левый нижний угол крючка должен оставаться на горизонтальной линии, что дает крючку две степени свободы.

Декомпозиция с помощью коробок, охватывающих конфигурационное пространство: Земляное покрытие X ⁻ является объединением всех красных прямоугольников и грунтового покрытия X ⁺ представляет собой объединение красных и зеленых коробок. Путь соответствует движению, представленному выше.

Эта цифра соответствует тому же пути, что и выше, но получена с гораздо меньшим количеством ящиков. Алгоритм избегает деления блоков пополам в тех частях конфигурационного пространства, которые не влияют на конечный результат.

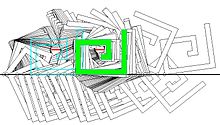
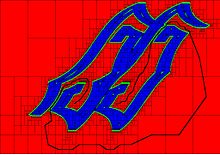
Николя Делану показал, что декомпозиция с использованием подмощений с использованием интервального анализа также позволяет охарактеризовать топологию C _free , например, подсчитав количество ее связных компонентов.

Геометрические алгоритмы

Наведите роботов среди полигональных препятствий

• График видимости
• Разложение клеток
• Диаграмма Вороного

Перемещение предметов среди препятствий

• сумма Минковского

Находим выход из здания

• самый дальний след луча

Учитывая пучок лучей вокруг текущей позиции, длина которых соответствует стене, робот движется в направлении самого длинного луча, если не определена дверь. Такой алгоритм использовался для моделирования аварийного выхода из зданий.

Искусственные потенциальные поля

Один из подходов состоит в том, чтобы рассматривать конфигурацию робота как точку в потенциальном поле, сочетающую притяжение к цели и отталкивание от препятствий. Полученная траектория выводится как путь. Этот подход имеет преимущества в том, что траектория создается с небольшими вычислениями. Однако они могут попасть в ловушку локальных минимумов потенциального поля и не найти пути или найти неоптимальный путь. Искусственные потенциальные поля можно рассматривать как уравнения континуума, аналогичные электростатическим потенциальным полям (рассматривая робота как точечный заряд), или движение через поле можно дискретизировать с помощью набора лингвистических правил. Функция навигации или вероятностная навигационная функция Это своего рода искусственные потенциальные функции, которые не имеют минимальных точек, кроме целевой точки.

Алгоритмы на основе выборки

Алгоритмы на основе выборки представляют пространство конфигурации с дорожной картой выборочных конфигураций. Базовый алгоритм выбирает N конфигураций на C и сохраняет те из них, которые _можно использовать в качестве контрольных точек . Затем строится дорожная карта, которая соединяет две вехи P и Q, если отрезок линии PQ полностью _{свободен} от C. Опять же, обнаружение коллизий используется для проверки включения в C _free . Чтобы найти путь, соединяющий S и G, их добавляют в дорожную карту. Если путь в дорожной карте связывает S и G, планировщик добивается успеха и возвращает этот путь. нет пути _{Если нет, то причина не является окончательной: либо в C free} , либо планировщик не выбрал достаточное количество вех.

Эти алгоритмы хорошо работают для многомерных конфигурационных пространств, поскольку, в отличие от комбинаторных алгоритмов, время их работы не зависит (явно) экспоненциально от размерности C. Их также (как правило) существенно проще реализовать. Они вероятностно полны, что означает, что вероятность того, что они дадут решение, приближается к 1 по мере того, как затрачивается больше времени. Однако они не могут определить, существует ли решение.

С учетом основных условий видимости на C _free было доказано, что по мере роста числа конфигураций N вероятность того, что приведенный выше алгоритм найдет решение, экспоненциально приближается к 1. Видимость не зависит явно от размерности C; возможно иметь многомерное пространство с «хорошей» видимостью или низкомерное пространство с «плохой» видимостью. Экспериментальный успех методов, основанных на выборке, предполагает, что наиболее часто встречающиеся пространства имеют хорошую видимость.

Существует множество вариантов этой базовой схемы:

• Обычно гораздо быстрее тестировать только сегменты между соседними парами вех, а не все пары.
• Неравномерное распределение выборки пытается разместить больше вех в областях, которые улучшают связность дорожной карты.
• Квазислучайные выборки обычно обеспечивают лучшее покрытие конфигурационного пространства, чем псевдослучайные , хотя в некоторых недавних работах утверждается, что эффект источника случайности минимален по сравнению с эффектом распределения выборки.
• Использует местную выборку путем выполнения направленного по Монте-Карло цепи Маркова случайного блуждания с некоторым локальным распределением предложений.
• Можно существенно сократить количество вех, необходимых для решения данной задачи, разрешив кривые прицелы (например, ползая по препятствиям, блокирующим путь между двумя вехами). ).
• Если необходим только один или несколько запросов на планирование, не всегда необходимо строить дорожную карту всего пространства. В этом случае варианты с выращиванием деревьев обычно работают быстрее (планирование с одним запросом). Дорожные карты по-прежнему полезны, если в одном пространстве необходимо выполнить множество запросов (планирование нескольких запросов).

Список известных алгоритмов

• А*
• Д*
• Быстрое исследование случайного дерева
• Вероятностная дорожная карта

Полнота и производительность

Планировщик движений считается полным, если за конечное время он либо выдает решение, либо правильно сообщает, что его нет. Большинство полных алгоритмов основаны на геометрии. Производительность комплексного планировщика оценивается по его вычислительной сложности . Доказывая это свойство математически, нужно убедиться, что оно происходит за конечное время, а не только в асимптотическом пределе. Это особенно проблематично, если при конкретном методе доказательства возникают бесконечные последовательности (которые сходятся только в предельном случае), поскольку тогда теоретически алгоритм никогда не остановится. Обычно ошибочно полагают, что интуитивные «трюки» (часто основанные на индукции) сходятся, что происходит только для бесконечного предела. Другими словами, решение существует, но планировщик никогда о нем не сообщит. Таким образом, это свойство связано с полнотой по Тьюрингу и в большинстве случаев служит теоретической основой/руководством. Планировщики, основанные на методе грубой силы, всегда полны, но реализуемы только для конечных и дискретных установок.

На практике завершение работы алгоритма всегда можно гарантировать, используя счетчик, который допускает только максимальное количество итераций, а затем всегда останавливается с решением или без него. В системах реального времени это обычно достигается с помощью сторожевого таймера , который просто убивает процесс. Сторожевой таймер должен быть независимым от всех процессов (обычно реализуемых с помощью процедур обработки прерываний низкого уровня). Однако асимптотический случай, описанный в предыдущем абзаце, таким путем достичь не удастся. Он сообщит о лучшем из найденных на данный момент (что лучше, чем ничего) или об отсутствии, но не сможет правильно сообщить, что его нет. Все реализации, включая сторожевой таймер, всегда неполны (за исключением того, что все случаи могут быть оценены за конечное время).

Полнота может быть обеспечена только путем очень строгого математического доказательства правильности (часто с помощью инструментов и графических методов) и должна выполняться только специализированными экспертами, если приложение содержит информацию о безопасности. С другой стороны, опровергнуть полноту легко, поскольку нужно всего лишь найти один бесконечный цикл или один неверный результат. Формальная проверка/корректность алгоритмов — это отдельная область исследований. Правильная настройка этих тестовых случаев — весьма сложная задача.

Полнота разрешения — это свойство, при котором планировщик гарантированно найдет путь, если разрешение базовой сетки достаточно хорошее. Большинство планировщиков с полным разрешением основаны на сетке или интервалах. Вычислительная сложность планировщиков с полным разрешением зависит от количества точек в базовой сетке, которое составляет O(1/h ^д ), где h — разрешение (длина одной стороны ячейки сетки), а d — размерность конфигурационного пространства.

Вероятностная полнота — это свойство, заключающееся в том, что по мере выполнения большего количества «работы» вероятность того, что планировщику не удастся найти путь, если он существует, асимптотически приближается к нулю. Некоторые методы, основанные на выборке, являются вероятностно полными. Производительность вероятностно полного планировщика измеряется скоростью сходимости. Для практических приложений обычно используют это свойство, поскольку оно позволяет настроить тайм-аут сторожевого таймера на основе среднего времени сходимости.

Неполные планировщики не всегда создают возможный путь, если он существует (см. первый абзац). Иногда неполные планировщики действительно хорошо работают на практике, поскольку они всегда останавливаются по истечении гарантированного времени и позволяют другим процедурам взять верх.

Варианты проблемы

Для решения вариантов этой основной проблемы было разработано множество алгоритмов.

Дифференциальные ограничения

Голономный

• Манипуляторы (с динамикой)

неголономный

• Дроны
• Автомобили
• Одноколесные велосипеды
• Самолеты
• Системы, ограниченные ускорением
• Движущиеся препятствия (время не может идти назад)
• Управляемая игла со скошенным кончиком
• Роботы с дифференциальным приводом

Гибридные системы

Гибридные системы — это системы, сочетающие дискретное и непрерывное поведение. Примерами таких систем являются:

• Роботизированные манипуляции
• Механическая сборка
• ножного робота Передвижение
• Реконфигурируемые роботы

Неопределенность

• Неопределенность движения
• Недостающая информация
• Активное зондирование
• Безсенсорное планирование
• Сетевые системы управления

Экологические ограничения

• Карты динамики

Приложения

• Робот-навигация
• Автоматизация
• Беспилотный автомобиль
• Роботизированная хирургия
• Цифровая анимация персонажей
• Складывание белка
• Безопасность и доступность в автоматизированном архитектурном проектировании

См. также

• Замок карданного подвеса - аналогичная традиционная проблема в машиностроении.
• Кинодинамическое планирование
• Проблема альпинизма
• OMPL — открытая библиотека планирования движения
• Поиск пути
• Проблемы с движением гальки – планирование движения нескольких роботов
• Задача о кратчайшем пути
• Скорость препятствия

Дальнейшее чтение

• Латомбе, Жан-Клод (2012). Планирование движения робота . Springer Science & Business Media. ISBN  978-1-4615-4022-9 .
• Алгоритмы планирования , Стивен М. ЛаВалль, 2006, издательство Кембриджского университета, ISBN   0-521-86205-1 .
• Принципы движения роботов: теория, алгоритмы и реализация , Х. Чозет, В. Бургард, С. Хатчинсон, Г. Кантор, Л. Е. Кавраки , К. Линч и С. Трун, MIT Press, апрель 2005 г.
• Марк де Берг; Марк ван Кревелд; Марк Овермарс и Отфрид Шварцкопф (2000). Вычислительная геометрия (2-е исправленное изд.). Издательство Спрингер . ISBN  978-3-540-65620-3 . Глава 13: Планирование движения робота: стр. 267–290.

Внешние ссылки

• «Виртуальная среда автоматизации открытой робототехники», http://openrave.org/
• Жан-Клод Латомб рассказывает о своей работе с роботами и планировании движений, 5 апреля 2000 г.
• «Открытая библиотека планирования движения ( OMPL )», http://ompl.kavrakilab.org
• «Библиотека стратегий движения», http://msl.cs.uiuc.edu/msl/
• «Комплект планирования движения», https://ai.stanford.edu/~mitul/mpk
• «Симокс», http://simox.sourceforge.net
• «Планирование и управление движением робота», http://www.laas.fr/%7Ejpl/book.html