- ₅ многогранник

Орфографические проекции
Самолет ₅ Кокстера
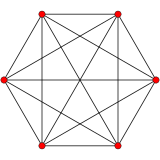5-симплекс

В 5-мерной геометрии существует 19 однородных многогранников с _A5 симметрией . Имеется одна самодвойственная правильная форма — 5-симплекс с 6 вершинами.

Каждую из них можно визуализировать как симметричные орфографические проекции в плоскостях Кокстера группы А ₅ Кокстера и других подгрупп.

Графики

Симметричные ортогональные проекции этих 19 многогранников можно построить в _{A 5} , A ₄ , A ₃ , A ₂ плоскостях Кокстера . A _k Графы имеют симметрию [k+1] . Для четных k и симметрично nodea_1ed-диаграмм симметрия удваивается до [2(k+1)] .

Каждый из этих 19 многогранников показан в этих 4 плоскостях симметрии, с нарисованными вершинами и ребрами, а вершины окрашены в соответствии с количеством перекрывающихся вершин в каждой проективной позиции.

#	плоскости Кокстера Графики				Диаграмма Кокстера-Динкина Символ Шлефли Имя
	[6]	[5]	[4]	[3]
	A_А5	A ₄	A_А3	A_А2
1					{3,3,3,3} 5-симплекс (хикс)
2					t ₁ {3,3,3,3} или r{3,3,3,3} Выпрямленный 5-симплекс (rix)
3					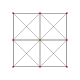т ₂ {3,3,3,3} или 2р{3,3,3,3} Биректифицированный 5-симплекс (точка)
4					т _0,1 {3,3,3,3} или т{3,3,3,3} Усеченный 5-симплекс (тикс)
5					т _1,2 {3,3,3,3} или 2т{3,3,3,3} Усеченный 5-симплекс (bittix)
6					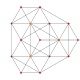т _0,2 {3,3,3,3} или рр{3,3,3,3} Кантелляционный 5-симплекс (саркс)
7					т _1,3 {3,3,3,3} или 2рр{3,3,3,3} Бикантеллированный 5-симплекс (сибрид)
8					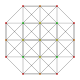т _0,3 {3,3,3,3} Ранцинированный 5-симплекс (спикс)
9					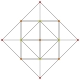т _0,4 {3,3,3,3} или 2р2р{3,3,3,3} Стерический 5-симплекс (ставрида)
10					т _0,1,2 {3,3,3,3} или тр{3,3,3,3} Кантиусеченный 5-симплекс (гаркс)
11					т _1,2,3 {3,3,3,3} или 2тр{3,3,3,3} Бикантиусеченный 5-симплекс (гибридный)
12					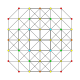т _0,1,3 {3,3,3,3} Ранцитусеченный 5-симплекс (паттикс)
13					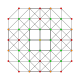т _0,2,3 {3,3,3,3} Рунцикантеллярный 5-симплекс (пиркс)
14					т _0,1,4 {3,3,3,3} Стеритусеченный 5-симплекс (капикс)
15					т _0,2,4 {3,3,3,3} Стерицантеллированный 5-симплекс (карточка)
16					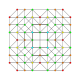т _0,1,2,3 {3,3,3,3} Ранчикантиусеченный 5-симплекс (гиппикс)
17					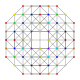т _0,1,2,4 {3,3,3,3} Стерикантиусеченный 5-симплекс (когракс)
18					т _0,1,3,4 {3,3,3,3} Стерирунный усеченный 5-симплекс (каптид)
19					т _0,1,2,3,4 {3,3,3,3} Всеусеченный 5-симплекс (гокад)

Многогранники А5
t₀	t₁	t₂	t_0,1	t_0,2	t_1,2	t_0,3
t_1,3	t_0,4	t_0,1,2	t_0,1,3	t_0,2,3	t_1,2,3	t_0,1,4
t_0,2,4	t_0,1,2,3	t_0,1,2,4	t_0,1,3,4	t_0,1,2,3,4

Ссылки

ХСМ Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
Калейдоскопы: избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона и Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 ^[1]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380–407, МР 2, 10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.

Внешние ссылки

Клитцинг, Ричард. «5D однородные многогранники (политеры)» .

Примечания

^ Wiley:: Калейдоскопы: Избранные сочинения HSM Коксетера

v т и Фундаментальные выпуклые правильные и однородные многогранники размерностей 2–10.
Семья	н	Б _н	И ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ж ₄ / Г ₂	Ч _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16 ячеек • Тессеракт	Демитессеракт	24-ячеечный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Равномерный n - многогранник	n - симплекс	n - ортоплекс • n - куб	n - демикуб	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений.

[1] Wiley:: Калейдоскопы: Избранные сочинения HSM Коксетера

[1]