Стерические 5-симплексы

5-симплекс	Стерический 5-симплекс
Стеритусеченный 5-симплекс	Стериконтеллярный 5-симплекс
Стерикантиусеченный 5-симплекс	Стерунцитусеченный 5-симплекс
Стерирунциантитусеченный 5-симплекс (Всеусеченный 5-симплекс)
Ортогональные проекции в A 5 и A 4. плоскостях Кокстера

В пятимерной геометрии стерилизованный 5-симплекс — это выпуклый однородный 5-многогранник ) четвертого порядка с усечениями ( стерикацией правильного 5-симплекса .

Существует шесть уникальных стерикаций 5-симплекса, включая перестановки усечений, кантелляций и сокращений. Простейший стерилизованный 5-симплекс также называют расширенным 5-симплексом с окольцованными первым и последним узлами, поскольку его можно построить с помощью операции расширения, примененной к обычному 5-симплексу. Высшую форму, стерильно-усеченный 5-симплекс , проще назвать омниусеченным 5-симплексом со всеми окольцованными узлами.

Стерический 5-симплекс

Стерический 5-симплекс
Тип	Равномерный 5-многогранник
Символ Шлефли	2р2р{3,3,3,3} 2р{3 2,2 } = $2r\left\{{\begin{array}{l}3,3\\3,3\end{array}}\right\}$
Диаграмма Кокстера-Динкина	или
4-ликий	62	6+6 {3,3,3} 15+15 {}×{3,3} 20 {3}×{3}
Клетки	180	60 {3,3} 120 {}×{3}
Лица	210	120 {3} 90 {4}
Края	120
Вершины	30
Вершинная фигура	Тетраэдрическая антипризма
Группа Коксетера	А 5 ×2, [[3,3,3,3]], порядок 1440
Характеристики	выпуклый , изогональный , изотоксальный

Стерилизованный 5-симплекс может быть построен с помощью операции расширения , примененной к обычному 5-симплексу , поэтому его также иногда называют расширенным 5-симплексом . Он имеет 30 вершин , 120 ребер , 210 граней (120 треугольников и 90 квадратов ), 180 ячеек (60 тетраэдров и 120 треугольных призм ) и 62 4-грани (12 5-клеток , 30 тетраэдрических призм и 20 3-3 дуопризм ).

Альтернативные названия

• Расширенный 5-симплекс
• Стерический гексатерон
• Маленький клеточный додекатерон (аббревиатура: ставрида) (Джонатан Бауэрс)

Сечения

Максимальное поперечное сечение стеризованного гексатерона с 4-мерной гиперплоскостью представляет собой укороченную 5-клетку . Это поперечное сечение делит стерилизованный гексатерон на две пентахоральные гиперкуполы, состоящие из 6 5-клеток , 15 тетраэдрических призм и 10 3-3 дуопризм каждая.

Вершины стерилизованного 5-симплекса можно построить на гиперплоскости в 6-мерном пространстве как перестановки (0,1,1,1,1,2). Это представляет собой положительную ортантную грань стеризованного 6-ортоплекса .

Вторая конструкция в 6-мерном пространстве из центра выпрямленного 6-ортоплекса задается координатными перестановками:

(1,-1,0,0,0,0)

Декартовы координаты в 5-мерном пространстве для нормализованных вершин стеризованного гексатерона с центром в начале координат:

$\left(\pm 1,\ 0,\ 0,\ 0,\ 0\right)$

$\left(0,\ \pm 1,\ 0,\ 0,\ 0\right)$

$\left(0,\ 0,\ \pm 1,\ 0,\ 0\right)$

$\left(\pm 1/2,\ 0,\ \pm 1/2,\ -{\sqrt {1/8}},\ -{\sqrt {3/8}}\right)$

$\left(\pm 1/2,\ 0,\ \pm 1/2,\ {\sqrt {1/8}},\ {\sqrt {3/8}}\right)$

$\left(0,\ \pm 1/2,\ \pm 1/2,\ -{\sqrt {1/8}},\ {\sqrt {3/8}}\right)$

$\left(0,\ \pm 1/2,\ \pm 1/2,\ {\sqrt {1/8}},\ -{\sqrt {3/8}}\right)$

$\left(\pm 1/2,\ \pm 1/2,\ 0,\ \pm {\sqrt {1/2}},\ 0\right)$

Корневая система

Его 30 вершин представляют корневые векторы простой группы Ли A ₅ . Это также вершинная фигура сот 5-симплексных .

Изображения

орфографические проекции

К ​ Самолет Коксетера	AА5	A 4
График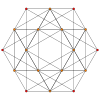
Двугранная симметрия	[6]	[[5]]=[10]
К ​ Самолет Коксетера	AА3	AА2
График
Двугранная симметрия	[4]	[[3]]=[6]

ортогональная проекция с симметрией [6]

Стеритусеченный 5-симплекс

Стеритусеченный 5-симплекс
Тип	Равномерный 5-многогранник
Символ Шлефли	т 0,1,4 {3,3,3,3}
Диаграмма Кокстера-Динкина
4-ликий	62	6 т{3,3,3} 15 {}× t{3,3} 20 {3}×{6} 15 {}× {3,3} 6 т 0,3 {3,3,3}
Клетки	330
Лица	570
Края	420
Вершины	120
Вершинная фигура
Группа Коксетера	А 5 [3,3,3,3], порядок 720
Характеристики	выпуклый , изогональный

Альтернативные названия

• Стеритусеченный гексатерон
• Целлипризматический гексатерон (аббревиатура: cappix) (Джонатан Бауэрс)

Координаты

Координаты могут быть заданы в 6-мерном пространстве как 180 перестановок:

(0,1,1,1,2,3)

Эта конструкция существует как одна из 64 ортантных граней стериусеченного 6-ортоплекса .

Изображения

орфографические проекции

К ​ Самолет Коксетера	AА5	A 4
График
Двугранная симметрия	[6]	[5]
К ​ Самолет Коксетера	AА3	AА2
График
Двугранная симметрия	[4]	[3]

Стериконтеллярный 5-симплекс

Стериконтеллярный 5-симплекс
Тип	Равномерный 5-многогранник
Символ Шлефли	т 0,2,4 {3,3,3,3}
Диаграмма Кокстера-Динкина	или
4-ликий	62	12 рр{3,3,3} 30 рр{3,3}х {} 20 {3}×{3}
Клетки	420	60 руб{3,3} 240 {}×{3} 90 {}×{}×{} 30р {3,3}
Лица	900	360 {3} 540 {4}
Края	720
Вершины	180
Вершинная фигура
Группа Коксетера	А 5 ×2, [[3,3,3,3]], порядок 1440
Характеристики	выпуклый , изогональный

Альтернативные названия

• Стериконтеллярный гексатерон
• Целлиромбовидный додекатерон (аббревиатура: карта) (Джонатан Бауэрс)

Координаты

Координаты могут быть заданы в 6-мерном пространстве как перестановки:

(0,1,1,2,2,3)

Эта конструкция существует как одна из 64 ортантных граней стерикантеллированного 6-ортоплекса .

Изображения

орфографические проекции

К ​ Самолет Коксетера	AА5	A 4
График
Двугранная симметрия	[6]	[[5]]=[10]
К ​ Самолет Коксетера	AА3	AА2
График
Двугранная симметрия	[4]	[[3]]=[6]

Стерикантиусеченный 5-симплекс

Стерикантиусеченный 5-симплекс
Тип	Равномерный 5-многогранник
Символ Шлефли	т 0,1,2,4 {3,3,3,3}
Диаграмма Кокстера-Динкина
4-ликий	62
Клетки	480
Лица	1140
Края	1080
Вершины	360
Вершинная фигура
Группа Коксетера	А 5 [3,3,3,3], порядок 720
Характеристики	выпуклый , изогональный

Альтернативные названия

• Стерикантиусеченный гексатерон
• Целлигреаторомбовидный гексатерон (аббревиатура: cograx) (Джонатан Бауэрс)

Координаты

Координаты могут быть заданы в 6-мерном пространстве как 360 перестановок:

(0,1,1,2,3,4)

Эта конструкция существует как одна из 64 ортантных граней стерикантиусеченного 6-ортоплекса .

Изображения

орфографические проекции

К ​ Самолет Коксетера	AА5	A 4
График
Двугранная симметрия	[6]	[5]
К ​ Самолет Коксетера	AА3	AА2
График
Двугранная симметрия	[4]	[3]

Стерунцитусеченный 5-симплекс

Стерунцитусеченный 5-симплекс
Тип	Равномерный 5-многогранник
Символ Шлефли	т 0,1,3,4 {3,3,3,3} 2т{3 2,2 }
Диаграмма Кокстера-Динкина	или
4-ликий	62	12 т 0,1,3 {3,3,3} 30 {}× t{3,3} 20 {6}×{6}
Клетки	450
Лица	1110
Края	1080
Вершины	360
Вершинная фигура
Группа Коксетера	А 5 ×2, [[3,3,3,3]], порядок 1440
Характеристики	выпуклый , изогональный

Альтернативные названия

• Стерирунный усеченный гексатерон
• Целлипризматоусеченный додекатерон (аббревиатура: каптид) (Джонатан Бауэрс)

Координаты

Координаты могут быть заданы в 6-мерном пространстве как 360 перестановок:

(0,1,2,2,3,4)

Эта конструкция существует как одна из 64 ортантных граней стерильно -усеченного 6-ортоплекса .

Изображения

орфографические проекции

К ​ Самолет Коксетера	AА5	A 4
График
Двугранная симметрия	[6]	[[5]]=[10]
К ​ Самолет Коксетера	AА3	AА2
График
Двугранная симметрия	[4]	[[3]]=[6]

Всеусеченный 5-симплекс

Всеусеченный 5-симплекс
Тип	Равномерный 5-многогранник
Символ Шлефли	т 0,1,2,3,4 {3,3,3,3} 2тр{3 2,2 }
Коксетер-Дынкин диаграмма	или
4-ликий	62	12 т 0,1,2,3 {3,3,3} 30 {}×tr{3,3} 20 {6}×{6}
Клетки	540	360 т{3,4} 90 {4,3} 90 {}×{6}
Лица	1560	480 {6} 1080 {4}
Края	1800
Вершины	720
Вершинная фигура	Нерегулярный 5-клеточный
Группа Коксетера	А 5 ×2, [[3,3,3,3]], порядок 1440
Характеристики	выпуклый , изогональный , зонотоп

Омниусеченный 5-симплекс имеет 720 вершин , 1800 ребер , 1560 граней (480 шестиугольников и 1080 квадратов ), 540 ячеек (360 усеченных октаэдров , 90 кубов и 90 шестиугольных призм ) и 62 четырехгранника (12 всеусеченных 5-клеток ). 30 усеченных октаэдрических призм и 20 6-6 дуопризм ).

Альтернативные названия

• Steriruncicantitусеченный 5-симплекс (Полное описание омниусечения 5-многогранников Джонсона)
• Всеусеченный гексатерон
• Большой клеточный додекатерон (аббревиатура: gocad) (Джонатан Бауэрс)

Координаты

Вершины всеусеченного 5-симплекса проще всего построить на гиперплоскости в 6-мерном пространстве как перестановки (0,1,2,3,4,5). Эти координаты берутся из положительной ортантной грани стерильно -усеченного 6-ортоплекса , t _0,1,2,3,4 {3 ⁴ ,4}, .

Изображения

орфографические проекции

К ​ Самолет Коксетера	AА5	A 4
График
Двугранная симметрия	[6]	[[5]]=[10]
К ​ Самолет Коксетера	AА3	AА2
График
Двугранная симметрия	[4]	[[3]]=[6]

Стереографическая проекция

Пермутоэдр

Всеусеченный 5-симплекс — это пермутоэдр шестого порядка. Это также зонотоп , сумма Минковского шести отрезков, параллельных шести прямым, проходящим через начало координат, и шести вершинам 5-симплекса.

Ортогональная проекция , вершины помечены как пермутоэдр .

Связанные соты

Всеусеченные 5-симплексные соты состоят из омниусеченных 5-симплексных граней с 3 гранями вокруг каждого гребня . Имеется Кокстера-Динкина . диаграмма .

Группа Коксетера	${\tilde {I}}_{1}$	${\tilde {A}}_{2}$	${\tilde {A}}_{3}$	${\tilde {A}}_{4}$	${\tilde {A}}_{5}$
Коксетер-Дынкин
Картина
Имя	Апейрогон	Гекстиль	Всеусеченный 3-симплекс соты	Всеусеченный 4-симплекс соты	Всеусеченный 5-симплекс соты
Фасеты

Полный курносый 5-симплекс

Полный курносый 5-симплекс или омниснуб 5-симплекс , определяемый как чередование всеусеченного 5-симплекса, не является однородным, но его можно представить диаграммой Коксетера. и симметрия [[3,3,3,3]] ⁺ , и построен из 12 курносых 5-ячеек , 30 курносых тетраэдрических антипризм , 20 3-3 дуоантипризм и 360 неправильных 5-ячеек, заполняющих промежутки в удаленных вершинах.

Связанные однородные многогранники

Эти многогранники являются частью 19 однородных 5-многогранников, основанных на группе [3,3,3,3] Кокстера , все они показаны здесь в _{A 5} плоскости Кокстера ортогональных проекциях . (Вершины окрашены в порядке перекрытия проекций: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый с увеличением количества вершин)

показывать Многогранники А5
t0	t1	t2	t0,1	t0,2	t1,2	t0,3
t1,3	t0,4	t0,1,2	t0,1,3	t0,2,3	t1,2,3	t0,1,4
t0,2,4	t0,1,2,3	t0,1,2,4	t0,1,3,4	t0,1,2,3,4

Ссылки

• ХСМ Коксетер :
  • HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
  • Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1]
    • (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
    • (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
    • (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
• Нормана Джонсона Равномерные многогранники , Рукопись (1991)
  • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
• Клитцинг, Ричард. «5D однородные многогранники (политеры)» . x3o3o3o3x - скад, x3x3o3o3x - каппикс, x3o3x3o3x - карта, x3x3x3o3x - когракс, x3x3o3x3x - каптид, x3x3x3x3x - gocad

Внешние ссылки

• Глоссарий по гиперпространству , Георгий Ольшевский.
• Многогранники различных размерностей
• Многомерный глоссарий