Призматическая еда

Призматоид с параллельными гранями A ₁ и A ₃ , средним поперечным сечением A ₂ и высотой h.

В геометрии призматоид многогранник — это , которого все вершины лежат в двух параллельных плоскостях . Его боковые грани могут представлять собой трапеции или треугольники . Если обе плоскости имеют одинаковое количество вершин, а боковые грани представляют собой либо параллелограммы , либо трапеции, то она называется призмоидой .

Объем

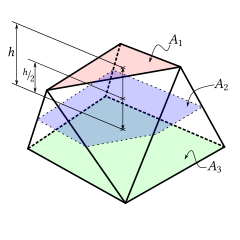
Если площади двух параллельных граней равны A ₁ и A ₃ , площадь поперечного сечения пересечения призматоида с плоскостью на полпути между двумя параллельными гранями равна A ₂ , а высота (расстояние между двумя параллельными гранями ) равно h , то объем призматоида определяется выражением $$V={\frac {h(A_{1}+4A_{2}+A_{3})}{6}}.$$Эта формула следует непосредственно путем интегрирования площади, параллельной двум плоскостям вершин, по правилу Симпсона , поскольку это правило точно для интегрирования многочленов степени до 3, и в этом случае площадь является не более чем квадратичной функцией по высоте.

Призматоидные семейства

Пирамиды	клинья	Параллелепипеды	Призмы	Антипризма			Купола	Хлыст

Семейства призматоидов включают:

• Пирамиды , у которых одна плоскость содержит только одну точку;
• Клинья , у которых одна плоскость содержит всего две точки;
• Призмы , многоугольники которых в каждой плоскости конгруэнтны и соединены прямоугольниками или параллелограммами;
• Антипризмы , многоугольники которых в каждой плоскости конгруэнтны и соединены чередующейся полосой треугольников;
• Звездные антипризмы ;
• Купола , у которых многоугольник в одной плоскости содержит в два раза больше точек, чем в другой, и соединяется с ним чередующимися треугольниками и прямоугольниками;
• Фруста получается усечением пирамиды или конуса;
• Четырехгранные шестигранные призматоиды :
  1. Параллелепипеды – шесть параллелограмма. граней
  2. Ромбоэдры – шесть граней ромба.
  3. Треугольные трапеции - шесть равных граней ромба.
  4. Кубоиды – шесть прямоугольных граней.
  5. Четырехсторонняя усеченная пирамида – вершина – усеченная квадратная пирамида.
  6. Куб – шесть квадратных граней

Высшие измерения

Купол четырехгранно-кубооктаэдрический.

В общем случае многогранник является призматоидальным, если его вершины существуют в двух гиперплоскостях . Например, в четырех измерениях два многогранника можно разместить в двух параллельных трехмерных пространствах и соединить многогранными сторонами.

Внешние ссылки

• Вайсштейн, Эрик В. «Призматоид» . Математический мир .