Кубовидный
В геометрии кубоид с шестью — это четырёхгранный выпуклый шестигранник , многогранник гранями.
Описание
[ редактировать ]Кубоид — это шестигранник с четырехугольными гранями, то есть многогранник с шестью гранями. Он имеет восемь вершин и двенадцать ребер. Этимологически «кубовидный» означает «подобный кубу » в смысле выпуклого твердого тела, которое можно превратить в куб, регулируя длину его ребер и углы между соседними гранями . Кубоид – это выпуклый многогранник, граф многогранника которого такой же, как у куба. [ 1 ] [ 2 ]
Кубоиды имеют разные типы. Особым случаем кубоида является прямоугольный кубоид с шестью прямоугольными гранями и смежными гранями, встречающимися под прямым углом . Когда все ребра прямоугольного кубоида имеют одинаковую длину, получается куб с шестью квадратными гранями и смежными гранями, встречающимися под прямым углом. [ 1 ] [ 3 ] Наряду с прямоугольными кубоидами, параллелепипед представляет собой кубоид с шестью параллелограммами . Ромбоэдр – это кубоид с шестью гранями ромба . квадрат Усеченный — это усеченный квадрат с квадратным основанием, но остальные грани — четырехугольники. Усеченный квадрат образуется усечения вершины квадратной пирамиды . путем
Пытаясь классифицировать кубоиды по их симметрии, Робертсон (1983) обнаружил, что существует по крайней мере 22 различных случая, «из которых только около половины знакомы по формам повседневных предметов». [ 4 ]
| Изображение | Имя | Лица | Группа симметрии |
|---|---|---|---|
 |
Куб | 6 одинаковых квадратов | О ч , [4,3], (*432) заказать 48 |
 |
Трехугольный трапецоэдр | 6 равны ромбов | Д 3д , [2 + ,6], (2*3) заказать 12 |
 |
Прямоугольный кубоид | 3 пары прямоугольников | Д 2h , [2,2], (*222) заказать 8 |
 |
Правая ромбическая призма | 1 пара ромбов, 4 одинаковых квадрата | |
 |
Правый квадратный кусок | 2 несовпадающих квадрата 4 равные равнобедренные трапеции |
С 4в , [4], (*44) заказать 8 |
 |
Скрученный тригональный трапецоэдр | 6 равных четырехугольников | Д 3 , [2,3] + , (223) заказать 6 |
 |
Правая равнобедренно-трапециевидная призма | 1 пара равнобедренных трапеций; 1 , 2 или 3 (конгруэнтных) квадрата(а) |
?, ?, ? заказать 4 |
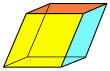 |
Ромбоэдр | 3 пары ромбов | С я , [2 + ,2 + ], (×) заказ 2 |
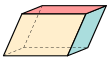 |
Параллелепипед | 3 пары параллелограммов |

Существуют шестигранники с четырехугольными гранями, которые не являются выпуклыми .
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Jump up to: а б Робертсон, Стюарт А. (1984). Многогранники и симметрия . Издательство Кембриджского университета . п. 75 . ISBN 9780521277396 .
- ^ Бранко Грюнбаум также использовал слово «кубовидный» для описания более общего класса выпуклых многогранников в трех или более измерениях, полученных путем склеивания многогранников, комбинаторно эквивалентных гиперкубам . Видеть: Грюнбаум, Бранко (2003). Выпуклые многогранники . Тексты для аспирантов по математике. Том. 221 (2-е изд.). Нью-Йорк: Springer-Publishing. п. 59. дои : 10.1007/978-1-4613-0019-9 . ISBN 978-0-387-00424-2 . МР 1976856 .
- ^ Дюпюи, Натан Ф. (1893). Элементы синтетической твердотельной геометрии . Макмиллан. п. 53 . Проверено 1 декабря 2018 г.
- ^ Робертсон, С.А. (1983). «Многогранники и симметрия». Математический интеллект . 5 (4): 57–60. дои : 10.1007/BF03026511 . МР 0746897 .