Телесный угол

Телесный угол
Телесный угол
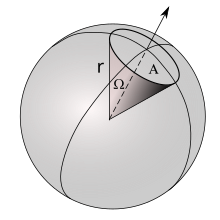	Визуальное представление телесного угла
Общие символы	Ой
И объединились	стерадиан
Другие подразделения	Квадратный градус , спат (угловая единица)
В базовых единицах СИ	м 2 /м 2
Сохранено ?	Нет
Выводы из ; другие количества
Измерение

В геометрии телесный угол (символ: $Ω$ ) является мерой величины поля зрения из некоторой конкретной точки, которую покрывает данный объект. То есть это мера того, насколько большим кажется объект наблюдателю, смотрящему с этой точки.Точка, из которой рассматривается объект, называется вершиной телесного угла, и говорят, что объект стягивает свой телесный угол в этой точке.

В Международной системе единиц (СИ) телесный угол выражается в безразмерной единице, называемой стерадианом (обозначение: ср). Один стерадиан соответствует одной единице площади единичной сферы, окружающей вершину, поэтому объект, блокирующий все лучи, исходящие от вершины, будет покрывать количество стерадианов, равное общей площади поверхности единичной сферы: $4\pi$ . Телесные углы также можно измерять в квадратах угловых мер, таких как градусы , минуты и секунды.

Небольшой объект поблизости может образовывать тот же телесный угол, что и более крупный объект, расположенный дальше. Например, хотя Луна намного меньше Солнца , она также намного ближе к Земле . Действительно, если смотреть из любой точки Земли, оба объекта имеют примерно одинаковый телесный угол (и, следовательно, видимый размер). Это очевидно во время солнечного затмения .

Определение и свойства

Телесный угол объекта в стерадианах равен площади сегмента единичной сферы с центром в вершине, которую покрывает объект. Указание площади сегмента единичной сферы в стерадианах аналогично указанию длины дуги единичного круга в радианах. Точно так же, как плоский угол в радианах — это отношение длины дуги к ее радиусу, телесный угол в стерадианах — это отношение площади, занимаемой предметом на сфере, к площади, определяемой квадратом радиуса дуги. сфера. Формула

$\Omega ={\frac {A}{r^{2}}},$

где $A$ - площадь сферической поверхности и $r$ – радиус рассматриваемой сферы.

Телесные углы часто используются в астрономии , физике и, в частности, астрофизике . Телесный угол объекта, находящегося очень далеко, примерно пропорционален отношению площади к квадрату расстояния. Здесь «площадь» означает площадь объекта, проецируемого в направлении обзора.

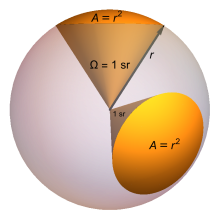
Телесный угол сферы, измеренный из любой точки внутри нее, равен 4 $π$ ср, а телесный угол, образуемый в центре куба одной из его граней, составляет одну шестую этого значения, или 2 $π$ /3 ср. Телесные углы также можно измерять в квадратных градусах (1 ср = ( 180/ $π$ ) ² квадратных градусах), в квадратных угловых минутах и квадратных угловых секундах или в долях сферы (1 ср = ⁠ 1/4 спат ( $π$ ⁠ дробная площадь), также известный как 1 сп = 4 $π$ ср).

В сферических координатах есть формула для дифференциала ,

$d\Omega =\sin \theta \,d\theta \,d\varphi ,$

где $θ$ — широта (угол от Северного полюса), а $φ$ — долгота.

Телесный угол для произвольно ориентированной поверхности $S,$ опирающейся в точку $P,$ равен телесному углу проекции поверхности $S$ на единичную сферу с центром $P$ , который можно вычислить как поверхностный интеграл :

$\Omega =\iint _{S}{\frac {{\hat {r}}\cdot {\hat {n}}}{r^{2}}}\,dS\ =\iint _{S}\sin \theta \,d\theta \,d\varphi ,$

где ${\hat {r}}={\vec {r}}/r$ — единичный вектор, соответствующий ${\vec {r}}$ , вектор положения бесконечно малой площади поверхности $dS$ относительно точки $P$ , и где ${\hat {n}}$ представляет единичный вектор нормали к $dS$ . Даже если проекция единичной сферы на поверхность $S$ не изоморфна , кратные складки правильно рассматриваются в соответствии с ориентацией поверхности, описываемой знаком скалярного произведения ${\hat {r}}\cdot {\hat {n}}$ .

Таким образом, можно аппроксимировать телесный угол, образуемый небольшой гранью, имеющей плоскую поверхность $dS$ , ориентацию ${\hat {n}}$ и расстояние $r$ от зрителя как:

$d\Omega =4\pi \left({\frac {dS}{A}}\right)\,({\hat {r}}\cdot {\hat {n}}),$

где площадь поверхности сферы A $π 4 r = 2$ .

Практическое применение

Определение силы света и яркости , а также соответствующих радиометрических величин силы излучения и сияния.
Вычисление сферического избытка $E$ сферического треугольника
Расчет потенциалов методом граничных элементов (МГЭ)
Оценку размеров лигандов в металлокомплексах см. Угол конуса лиганда.
Расчет электрического и магнитного поля вокруг распределений зарядов
Вывод закона Гаусса
Расчет излучательной мощности и излучения при теплопередаче
Расчет сечений резерфордовского рассеяния
Расчет сечений комбинационного рассеяния света
Телесный угол приемного конуса оптического волокна
Расчет узловой плотности в сетках. ^[1]

Твердые углы для обычных объектов

Конус, сферический колпачок, полусфера

Телесный угол конуса с вершиной в вершине телесного угла и с углом при вершине 2 $θ$ представляет собой площадь сферической шапки на единичной сфере.

$\Omega =2\pi \left(1-\cos \theta \right)\ =4\pi \sin ^{2}{\frac {\theta }{2}}.$

Для малых $θ$ таких, что $cos θ \approx 1 - θ 2 /2$ это сводится к $π θ 2$ , площадь круга.

Вышеуказанное можно найти путем вычисления следующего двойного интеграла с использованием единичного элемента поверхности в сферических координатах :

${\begin{aligned}\int _{0}^{2\pi }\int _{0}^{\theta }\sin \theta '\,d\theta '\,d\phi &=\int _{0}^{2\pi }d\phi \int _{0}^{\theta }\sin \theta '\,d\theta '\\&=2\pi \int _{0}^{\theta }\sin \theta '\,d\theta '\\&=2\pi \left[-\cos \theta '\right]_{0}^{\theta }\\&=2\pi \left(1-\cos \theta \right).\end{aligned}}$

Эту формулу можно вывести и без использования математических вычислений . Более 2200 лет назад Архимед доказал, что площадь поверхности сферической крышки всегда равна площади круга, радиус которого равен расстоянию от края сферической крышки до точки, где ось симметрии крышки пересекает крышку. ^[2] На диаграмме этот радиус обозначен как

$2r\sin {\frac {\theta }{2}}.$

Следовательно, для единичной сферы телесный угол сферической шапки определяется как

$\Omega =4\pi \sin ^{2}{\frac {\theta }{2}}=2\pi \left(1-\cos \theta \right).$

Когда $θ$ = ⁠ $π$ / 2 ⁠ сферическая крышка становится полусферой с телесным углом 2 $π$ .

Телесный угол дополнения конуса равен

$4\pi -\Omega =2\pi \left(1+\cos \theta \right)=4\pi \cos ^{2}{\frac {\theta }{2}}.$

Это также телесный угол той части небесной сферы , которую может видеть астрономический наблюдатель, находящийся на широте $θ,$ при вращении Земли. На экваторе видна вся небесная сфера; на каждом полюсе только одна половина.

Телесный угол, опирающийся на сегмент сферической шапки, рассеченный плоскостью под углом $γ$ от оси конуса и проходящей через вершину конуса, можно рассчитать по формуле ^[3]

$\Omega =2\left[\arccos \left({\frac {\sin \gamma }{\sin \theta }}\right)-\cos \theta \arccos \left({\frac {\tan \gamma }{\tan \theta }}\right)\right].$

Например, если $γ = - θ$ , то формула сводится к приведенной выше формуле сферической шапочки: первый член становится $π$ , а второй $π cos θ$ .

Тетраэдр

Пусть OABC — вершины тетраэдра с началом в точке O, опирающегося на треугольную грань ABC, где ${\vec {a}}\ ,\,{\vec {b}}\ ,\,{\vec {c}}$ являются векторными положениями вершин A, B и C. Определим угол вершины $θ a$ как угол BOC и определим $θ b$ , $θ c$ соответственно. Позволять $\phi _{ab}$ — двугранный угол между плоскостями, содержащими тетраэдрические грани OAC и OBC и определяющий $\phi _{ac}$ , $\phi _{bc}$ соответственно. Телесный угол $Ω,$ опирающийся на треугольную поверхность ABC, определяется выражением

$\Omega =\left(\phi _{ab}+\phi _{bc}+\phi _{ac}\right)\ -\pi .$

Это следует из теории сферического избытка и приводит к тому, что существует теорема, аналогичная теореме о том, что «Сумма внутренних углов плоского треугольника равна $π$ » , для суммы четырех внутренних телесных углов треугольника. тетраэдр следующим образом:

$\sum _{i=1}^{4}\Omega _{i}=2\sum _{i=1}^{6}\phi _{i}\ -4\pi ,$

где $\phi _{i}$ колеблется по всем шести двугранным углам между любыми двумя плоскостями, содержащими тетраэдрические грани OAB, OAC, OBC и ABC. ^[4]

Полезная формула для расчета телесного угла тетраэдра в начале координат O, которая является чисто функцией углов при вершинах $θ a$ , $θ b$ , $θ c,$ дается . теоремой Л'Юилье ^[5]^[6] как

$\tan \left({\frac {1}{4}}\Omega \right)={\sqrt {\tan \left({\frac {\theta _{s}}{2}}\right)\tan \left({\frac {\theta _{s}-\theta _{a}}{2}}\right)\tan \left({\frac {\theta _{s}-\theta _{b}}{2}}\right)\tan \left({\frac {\theta _{s}-\theta _{c}}{2}}\right)}},$

где $\theta _{s}={\frac {\theta _{a}+\theta _{b}+\theta _{c}}{2}}.$

Другая интересная формула предполагает выражение вершин как векторов в трехмерном пространстве. Позволять ${\vec {a}}\ ,\,{\vec {b}}\ ,\,{\vec {c}}$ — векторные позиции вершин A, B и C, и пусть $a$ , $b$ и $c$ — величина каждого вектора (расстояние от исходной точки). Телесный угол $Ω,$ опирающийся на треугольную поверхность ABC, равен: ^[7]^[8]

$\tan \left({\frac {1}{2}}\Omega \right)={\frac {\left|{\vec {a}}\ {\vec {b}}\ {\vec {c}}\right|}{abc+\left({\vec {a}}\cdot {\vec {b}}\right)c+\left({\vec {a}}\cdot {\vec {c}}\right)b+\left({\vec {b}}\cdot {\vec {c}}\right)a}},$

где $\left|{\vec {a}}\ {\vec {b}}\ {\vec {c}}\right|={\vec {a}}\cdot ({\vec {b}}\times {\vec {c}})$

обозначает скалярное тройное произведение трех векторов и ${\vec {a}}\cdot {\vec {b}}$ обозначает скалярное произведение .

Здесь необходимо соблюдать осторожность, чтобы избежать отрицательных или неправильных телесных углов. Одним из источников потенциальных ошибок является то, что скалярное тройное произведение может быть отрицательным, если $a$ , $b$ , $c$ имеют неправильную обмотку . Вычисление абсолютного значения является достаточным решением, поскольку никакая другая часть уравнения не зависит от обмотки. Другая ловушка возникает, когда скалярное тройное произведение положительно, а делитель отрицателен. В этом случае возвращается отрицательное значение, которое необходимо увеличить на $π$ .

Пирамида

Телесный угол четырехгранной прямоугольной пирамиды с при вершине углами $a$ и $b$ ( двугранные углы, измеренные к противоположным боковым граням пирамиды) равен $\Omega =4\arcsin \left(\sin \left({a \over 2}\right)\sin \left({b \over 2}\right)\right).$

Если известны длины сторон ( $α$ и $β$ ) основания пирамиды и расстояние ( $d$ ) от центра прямоугольника основания до вершины пирамиды (центра сферы), то приведенное выше уравнение можно манипулировать, чтобы дать

$\Omega =4\arctan {\frac {\alpha \beta }{2d{\sqrt {4d^{2}+\alpha ^{2}+\beta ^{2}}}}}.$

Телесный угол прямой $n-$ угольной пирамиды, основанием которой является правильный $n$ -сторонний многоугольник радиуса описанной окружности $r$ с высота $h$ пирамиды

$\Omega =2\pi -2n\arctan \left({\frac {\tan \left({\pi \over n}\right)}{\sqrt {1+{r^{2} \over h^{2}}}}}\right).$

Телесный угол произвольной пирамиды с $n$ -сторонним основанием, определяемым последовательностью единичных векторов, представляющих ребра ${s 1, s 2}, ... s n,$ можно эффективно вычислить следующим образом: ^[3]

$\Omega =2\pi -\arg \prod _{j=1}^{n}\left(\left(s_{j-1}s_{j}\right)\left(s_{j}s_{j+1}\right)-\left(s_{j-1}s_{j+1}\right)+i\left[s_{j-1}s_{j}s_{j+1}\right]\right).$

где круглые скобки (* *) — скалярное произведение , а квадратные скобки [* * *] — тройное скалярное произведение , а $i$ — мнимая единица . Индексы цикличны: $s 0 = s n$ и $s 1 = s n + 1$ . Комплексные произведения добавляют фазу, связанную с каждым углом вершины многоугольника. Однако кратное $2\pi$ теряется в срезанной ветке $\arg$ и их необходимо отслеживать отдельно. Кроме того, текущий продукт сложных фаз необходимо время от времени масштабировать, чтобы избежать недорасхода в пределе почти параллельных сегментов.

Прямоугольник широты и долготы

Телесный угол прямоугольника широты и долготы на земном шаре равен $\left(\sin \phi _{\mathrm {N} }-\sin \phi _{\mathrm {S} }\right)\left(\theta _{\mathrm {E} }-\theta _{\mathrm {W} }\,\!\right)\;\mathrm {sr} ,$ где $φ N$ и $φ S$ — северная и южная линии широты (измеряются от экватора в радианах с углом, увеличивающимся к северу), а $θ E$ и $θ W$ — восточная и западная линии долготы (где угол в радианах увеличивается к востоку). ^[9] Математически это представляет собой дугу с углом $φ N - φ S,$ огибающую сферу на $θ E - θ W$ радиан. Когда долгота составляет 2 $π$ радиан, а широта — $π$ радиан, телесный угол равен углу сферы.

Прямоугольник широты и долготы не следует путать с телесным углом прямоугольной пирамиды. Все четыре стороны прямоугольной пирамиды пересекают поверхность сферы по большим дугам . В прямоугольнике широта-долгота только линии долготы представляют собой большие дуги круга; линии широты нет.

Небесные объекты

Используя определение углового диаметра , формулу телесного угла небесного объекта можно определить через радиус объекта: ${\textstyle R}$ и расстояние от наблюдателя до объекта, $d$ :

$\Omega =2\pi \left(1-{\frac {\sqrt {d^{2}-R^{2}}}{d}}\right):d\geq R.$

Если ввести соответствующие средние значения для Солнца и Луны (по отношению к Земле), средний телесный угол Солнца составит 6,794 × 10. ⁻⁵ стерадианы, а средний телесный угол Луны составляет 6,418 × 10 . ⁻⁵ стерадианы. Что касается всей небесной сферы, Солнце и Луна составляют средние дробные площади 0,000 5406 % ( 5,406 ppm ) и 0,000 5107 % ( 5,107 ppm ) соответственно. Поскольку эти телесные углы примерно одинакового размера, Луна может вызывать как полное, так и кольцевое солнечное затмение в зависимости от расстояния между Землей и Луной во время затмения.

Телесные углы в произвольных размерах

Телесный угол, опирающийся на полную ( $d - 1$ )-мерную сферическую поверхность единичной сферы в $d$ -мерном евклидовом пространстве, может быть определен в любом количестве измерений $d$ . Этот коэффициент телесного угла часто необходим в расчетах со сферической симметрией. Оно определяется формулой $\Omega _{d}={\frac {2\pi ^{\frac {d}{2}}}{\Gamma \left({\frac {d}{2}}\right)}},$ где $Γ$ – гамма-функция . Когда $d$ является целым числом, гамма-функция может быть вычислена явно. ^[10] Отсюда следует, что $\Omega _{d}={\begin{cases}{\frac {1}{\left({\frac {d}{2}}-1\right)!}}2\pi ^{\frac {d}{2}}\ &d{\text{ even}}\\{\frac {\left({\frac {1}{2}}\left(d-1\right)\right)!}{(d-1)!}}2^{d}\pi ^{{\frac {1}{2}}(d-1)}\ &d{\text{ odd}}.\end{cases}}$

Это дает ожидаемые результаты в 4 $π$ стерадиана для трехмерной сферы, ограниченной поверхностью площадью $4π r. 2$ и 2 $π$ радиан для двумерного круга, ограниченного окружностью длиной $2π r$ . Это также дает немного менее очевидное значение 2 для одномерного случая, в котором одномерная «сфера» с центром в начале координат представляет собой интервал $[- r, r]$ и ограничена двумя предельными точками.

Аналог векторной формулы в произвольном измерении был выведен Аомото. ^[11]^[12]и независимо Рибандо. ^[13] Он выражает их как бесконечный многомерный ряд Тейлора : $\Omega =\Omega _{d}{\frac {\left|\det(V)\right|}{(4\pi )^{d/2}}}\sum _{{\vec {a}}\in \mathbb {N} _{0}^{\binom {d}{2}}}\left[{\frac {(-2)^{\sum _{i<j}a_{ij}}}{\prod _{i<j}a_{ij}!}}\prod _{i}\Gamma \left({\frac {1+\sum _{m\neq i}a_{im}}{2}}\right)\right]{\vec {\alpha }}^{\vec {a}}.$ Учитывая $d$ единичных векторов ${\vec {v}}_{i}$ определяя угол, пусть $V$ обозначает матрицу, образованную их объединением, так что $i$ -й столбец равен ${\vec {v}}_{i}$ , и $\alpha _{ij}={\vec {v}}_{i}\cdot {\vec {v}}_{j}=\alpha _{ji},\alpha _{ii}=1$ . Переменные $\alpha _{ij},1\leq i<j\leq d$ сформировать многовариантную ${\vec {\alpha }}=(\alpha _{12},\dotsc ,\alpha _{1d},\alpha _{23},\dotsc ,\alpha _{d-1,d})\in \mathbb {R} ^{\binom {d}{2}}$ . Для «конгруэнтной» целочисленной мультиэкспоненты ${\vec {a}}=(a_{12},\dotsc ,a_{1d},a_{23},\dotsc ,a_{d-1,d})\in \mathbb {N} _{0}^{\binom {d}{2}},$ определять ${\textstyle {\vec {\alpha }}^{\vec {a}}=\prod \alpha _{ij}^{a_{ij}}}$ . Обратите внимание, что здесь $\mathbb {N} _{0}$ = целые неотрицательные числа или натуральные числа, начинающиеся с 0. Обозначения $\alpha _{ji}$ для $j>i$ означает переменную $\alpha _{ij}$ , аналогично для показателей $a_{ji}$ . Следовательно, термин ${\textstyle \sum _{m\neq l}a_{lm}}$ означает сумму всех членов в ${\vec {a}}$ в котором l появляется либо как первый, либо как второй индекс.Там, где этот ряд сходится, он сходится к телесному углу, определяемому векторами.

Ссылки

^ Фалья, Ромен (2023). «Адаптация сетки для двумерных течений с ограниченной и свободной поверхностью методом конечных элементов» . Вычислительная механика частиц . 10 : 1049–1076.
^ «Архимед о сферах и цилиндрах» . Математические страницы . 2015.
^ Jump up to: ^а ^б Мазонка, Олег (2012). «Телесный угол конических поверхностей, многогранных конусов и пересекающихся сферических колпачков». arXiv : 1205.1396 [ math.MG ].
^ Хопф, Хайнц (1940). «Избранные главы геометрии» (PDF) . ETH Цюрих : 1–2. Архивировано (PDF) из оригинала 21 сентября 2018 г.
^ «Теорема Л'Юилье - из Wolfram MathWorld» . Mathworld.wolfram.com. 19 октября 2015 г. Проверено 19 октября 2015 г.
^ «Сферический избыток – из Wolfram MathWorld» . Mathworld.wolfram.com. 19 октября 2015 г. Проверено 19 октября 2015 г.
^ Эрикссон, Фольке (1990). «О мере телесных углов». Математика. Маг . 63 (3): 184–187. дои : 10.2307/2691141 . JSTOR 2691141 .
^ Ван Остером, А; Стреки, Дж (1983). «Телесный угол плоского треугольника». IEEE Транс. Биомед. англ . БМЭ-30 (2): 125–126. дои : 10.1109/TBME.1983.325207 . ПМИД 6832789 . S2CID 22669644 .
^ «Площадь прямоугольника широты и долготы» . Математический форум @ Drexel . 2003.
^ Джексон, FM (1993). «Многогранники в евклидовом n-пространстве» . Вестник Института математики и ее приложений . 29 (11/12): 172–174.
^ Аомото, Кадзухико (1977). «Аналитическая структура функции Шлефли» . Нагойская математика. Дж . 68 : 1–16. дои : 10.1017/s0027763000017839 .
^ Бек, М.; Робинс, С.; Сэм, СВ (2010). «Теоремы о положительности для полиномов телесных углов». Вклад в алгебру и геометрию . 51 (2): 493–507. arXiv : 0906.4031 . Бибкод : 2009arXiv0906.4031B .
^ Рибандо, Джейсон М. (2006). «Измерение телесных углов за пределами третьего измерения» . Дискретная и вычислительная геометрия . 36 (3): 479–487. дои : 10.1007/s00454-006-1253-4 .

Дальнейшее чтение

Джеффи, АХ (1954). «Твердый угол, образованный круглой апертурой в точечных и разбросанных источниках: формулы и некоторые таблицы». Преподобный учёный. Инструмент . 25 (4): 349–354. Бибкод : 1954RScI...25..349J . дои : 10.1063/1.1771061 .
Маскет, А. Виктор (1957). «Интегралы контура твердого угла, ряды и таблицы». Преподобный учёный. Инструмент . 28 (3): 191. Бибкод : 1957RScI...28..191M . дои : 10.1063/1.1746479 .
Наито, Минору (1957). «Метод расчета телесного угла, образованного круглым отверстием». Дж. Физ. Соц. Япония . 12 (10): 1122–1129. Бибкод : 1957JPSJ...12.1122N . дои : 10.1143/JPSJ.12.1122 .
Пакстон, Ф. (1959). «Расчет твердого угла для круглого диска» . Преподобный учёный. Инструмент . 30 (4): 254. Бибкод : 1959RScI...30..254P . дои : 10.1063/1.1716590 .
Хаджави, А. (1968). «Расчет телесного угла, образуемого прямоугольными отверстиями». J. Опт. Соц. Являюсь . 58 (10): 1417–1418. Бибкод : 1968JOSA...58.1417K . дои : 10.1364/JOSA.58.001417 .
Гарднер, Р.П.; Карнесейл, А. (1969). «Телесный угол, опирающийся в точке на круглый диск». Нукл. Инструмент. Методы . 73 (2): 228–230. Бибкод : 1969NucIM..73..228G . дои : 10.1016/0029-554X(69)90214-6 .
Гарднер, Р.П.; Вергезе, К. (1971). «О телесном угле, опирающемся на круглый диск». Нукл. Инструмент. Методы . 93 (1): 163–167. Бибкод : 1971NucIM..93..163G . дои : 10.1016/0029-554X(71)90155-8 .
Гото, Х.; Яги, Х. (1971). «Твердый угол, опирающийся на прямоугольную щель». Нукл. Инструмент. Методы . 96 (3): 485–486. Бибкод : 1971NucIM..96..485G . дои : 10.1016/0029-554X(71)90624-0 .
Кук, Дж. (1980). «Твердый угол, образованный двумя прямоугольниками». Нукл. Инструмент. Методы . 178 (2–3): 561–564. Бибкод : 1980NucIM.178..561C . дои : 10.1016/0029-554X(80)90838-1 .
Асвестас, Джон С..; Инглунд, Дэвид К. (1994). «Вычисление телесного угла, образуемого плоской фигурой». Опция англ . 33 (12): 4055–4059. Бибкод : 1994OptEn..33.4055A . дои : 10.1117/12.183402 . Опечатка там же. том 50 (2011), стр. 059801.
Трика, Станислав (1997). «Угловое распределение телесного угла в точке, опирающейся на круглый диск». Опция Коммун . 137 (4–6): 317–333. Бибкод : 1997OptCo.137..317T . дои : 10.1016/S0030-4018(96)00789-4 .
Прата, MJ (2004). «Аналитический расчет телесного угла, образуемого детектором круглого диска при точечном косинусном источнике». Нукл. Инструмент. Методы Физ. Рез. А. 521 (2–3): 576. arXiv : math-ph/0305034 . Бибкод : 2004NIMPA.521..576P . дои : 10.1016/j.nima.2003.10.098 . S2CID 15266291 .
Тимус, DM; Прата, MJ; Калла, СЛ; Аббас, Мичиган; Онер, Ф.; Гальяно, Э. (2007). «Некоторые дальнейшие аналитические результаты о телесном угле, стянутом в точке круглым диском с использованием эллиптических интегралов». Нукл. Инструмент. Методы Физ. Рез. А. 580 : 149–152. Бибкод : 2007NIMPA.580..149T . дои : 10.1016/j.nima.2007.05.055 .

Внешние ссылки

Артур П. Нортон, Звездный атлас, Галл и Инглис, Эдинбург, 1969.
М. Г. Кендалл, Курс геометрии N измерений, № 8 статистических монографий и курсов Гриффина, изд. М.Г. Кендалл, Charles Griffin & Co. Ltd, Лондон, 1961 г.
Вайсштейн, Эрик В. «Сплошной угол» . Математический мир .

[1] Фалья, Ромен (2023). «Адаптация сетки для двумерных течений с ограниченной и свободной поверхностью методом конечных элементов» . Вычислительная механика частиц . 10 : 1049–1076.

[2] «Архимед о сферах и цилиндрах» . Математические страницы . 2015.

[Mazonka-3] Jump up to: ^а ^б Мазонка, Олег (2012). «Телесный угол конических поверхностей, многогранных конусов и пересекающихся сферических колпачков». arXiv : 1205.1396 [ math.MG ].

[4] Хопф, Хайнц (1940). «Избранные главы геометрии» (PDF) . ETH Цюрих : 1–2. Архивировано (PDF) из оригинала 21 сентября 2018 г.

[5] «Теорема Л'Юилье - из Wolfram MathWorld» . Mathworld.wolfram.com. 19 октября 2015 г. Проверено 19 октября 2015 г.

[6] «Сферический избыток – из Wolfram MathWorld» . Mathworld.wolfram.com. 19 октября 2015 г. Проверено 19 октября 2015 г.

[7] Эрикссон, Фольке (1990). «О мере телесных углов». Математика. Маг . 63 (3): 184–187. дои : 10.2307/2691141 . JSTOR 2691141 .

[8] Ван Остером, А; Стреки, Дж (1983). «Телесный угол плоского треугольника». IEEE Транс. Биомед. англ . БМЭ-30 (2): 125–126. дои : 10.1109/TBME.1983.325207 . ПМИД 6832789 . S2CID 22669644 .

[9] «Площадь прямоугольника широты и долготы» . Математический форум @ Drexel . 2003.

[10] Джексон, FM (1993). «Многогранники в евклидовом n-пространстве» . Вестник Института математики и ее приложений . 29 (11/12): 172–174.

[11] Аомото, Кадзухико (1977). «Аналитическая структура функции Шлефли» . Нагойская математика. Дж . 68 : 1–16. дои : 10.1017/s0027763000017839 .

[12] Бек, М.; Робинс, С.; Сэм, СВ (2010). «Теоремы о положительности для полиномов телесных углов». Вклад в алгебру и геометрию . 51 (2): 493–507. arXiv : 0906.4031 . Бибкод : 2009arXiv0906.4031B .

[13] Рибандо, Джейсон М. (2006). «Измерение телесных углов за пределами третьего измерения» . Дискретная и вычислительная геометрия . 36 (3): 479–487. дои : 10.1007/s00454-006-1253-4 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]