алгебра Хопфа

В математике алгебра Хопфа , названная в честь Хайнца Хопфа , представляет собой структуру, которая одновременно является ( унитальной ассоциативной) алгеброй и (кунитальной коассоциативной) коалгеброй , причем совместимость этих структур делает ее биалгеброй , и которая, кроме того, снабжена антигомоморфизмом . удовлетворение определенного свойства. Теория представлений алгебры Хопфа особенно хороша, поскольку существование совместимых коумножений, коединицы и антипода позволяет строить тензорные произведения представлений, тривиальных представлений и двойственных представлений.

Алгебры Хопфа естественным образом встречаются в алгебраической топологии , где они возникли и связаны с концепцией H-пространства , в теории групповых схем , в теории групп (через концепцию группового кольца ) и во многих других местах, что делает их, вероятно, наиболее знакомый тип биалгебры . Алгебры Хопфа также изучаются сами по себе, с большим количеством работы над конкретными классами примеров, с одной стороны, и проблемами классификации, с другой. Они имеют разнообразные применения: от физики конденсированного состояния до квантовой теории поля. к теории струн и феноменология БАК .

Формальное определение

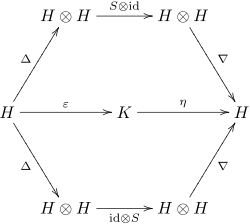
Формально алгебра Хопфа — это (ассоциативная и коассоциативная) биалгебра H над полем K вместе с K -линейным отображением S : H → H (называемым антиподом ) такая, что следующая диаграмма коммутирует :

Здесь Δ — коумножение биалгебры, ∇ — ее умножение, η — ее единица, ε — ее счетная единица. В безсуммированной нотации Свидлера это свойство можно также выразить как

$S(c_{(1)})c_{(2)}=c_{(1)}S(c_{(2)})=\varepsilon (c)1\qquad {\mbox{ for all }}c\in H.$

Что касается алгебр можно заменить основное поле K коммутативным кольцом R. , в приведенном выше определении

Определение алгебры Хопфа является самодвойственным (что отражено в симметрии приведенной выше диаграммы), поэтому, если можно определить двойственную к H ( что всегда возможно, если H конечномерна), то она автоматически является алгеброй Хопфа. .

Структурные константы

Закрепление основы $\{e_{k}\}$ для базового векторного пространства можно определить алгебру в терминах структурных констант для умножения:

$e_{i}\nabla e_{j}=\sum _{k}\mu _{\;ij}^{k}e_{k}$

для совместного умножения:

$\Delta e_{i}=\sum _{j,k}\nu _{i}^{\;jk}e_{j}\otimes e_{k}$

и антипод:

$Se_{i}=\sum _{j}\tau _{i}^{\;j}e_{j}$

Тогда ассоциативность требует, чтобы

$\mu _{\;ij}^{k}\mu _{\;kn}^{m}=\mu _{\;jn}^{k}\mu _{\;ik}^{m}$

тогда как коассоциативность требует, чтобы

$\nu _{k}^{\;ij}\nu _{i}^{\;mn}=\nu _{k}^{\;mi}\nu _{i}^{\;nj}$

Связующая аксиома требует, чтобы

$\nu _{k}^{\;ij}\tau _{j}^{\;m}\mu _{\;im}^{n}=\nu _{k}^{\;jm}\tau _{j}^{\,\;i}\mu _{\;im}^{n}$

Свойства антипода

антипод S Иногда требуется, чтобы имел K -линейный обратный, что происходит автоматически в конечномерном случае. , или если H коммутативен квазитреугольен или кокоммутативен (или, в более общем смысле, ) .

В общем случае S — антигомоморфизм , так что С ² является гомоморфизмом , который, следовательно, является автоморфизмом, если S обратима (что может потребоваться).

Если С ² = id _H , то алгебра Хопфа называется инволютивной (а лежащая в основе алгебра с инволюцией является *-алгеброй ). Если H конечномерно полупросто над полем нулевой характеристики, коммутативным или кокоммутативным, то оно инволютивно.

Если биалгебра B допускает антипод S , то S единственна («биалгебра допускает не более 1 структуры алгебры Хопфа»). Таким образом, антипод не задаёт никакой дополнительной структуры, которую мы можем выбрать: быть алгеброй Хопфа — это свойство биалгебры.

Антипод — это аналог карты инверсии группы, которая переводит g в g. ⁻¹ .

Подалгебры Хопфа

Подалгебра A алгебры Хопфа H является подалгеброй Хопфа, если она является подалгеброй H и антипод S отображает A в A . Другими словами, подалгебра Хопфа A сама по себе является алгеброй Хопфа, когда умножение, коумножение, коединица и антипод H ограничены A единица 1 H (и, кроме того, требуется, чтобы находилась в A). Теорема свободы Николса-Цёллера Уоррена Николса и Беттины Зеллер (1989) установила, что естественный A -модуль H свободен от конечного ранга, если H конечномерен: обобщение теоремы Лагранжа для подгрупп . Как следствие этой и интегральной теории, подалгебра Хопфа полупростой конечномерной алгебры Хопфа автоматически полупроста.

Подалгебра Хопфа A называется правонормальной в алгебре Хопфа H, если она удовлетворяет условию устойчивости ad _r ( h )( A ) ⊆ A для всех h в H , где правосопряженное отображение ad _r определяется формулой ad _р ( час )( а ) знак равно S ( час ₍₁₎ ) ах ₍₂₎ для всех a в A , h в H . Аналогично, подалгебра Хопфа A является нормальной слева в H, если она устойчива относительно левого сопряженного отображения, определенного формулой ad _l ( h )( a ) = h ₍₁₎ aS ( h ₍₂₎ ). Два условия нормальности эквивалентны, если антипод S биективен, и в этом случае A называется нормальной подалгеброй Хопфа.

Нормальная подалгебра Хопфа A в H удовлетворяет условию (равенства подмножеств H): HA ⁺ = А ⁺ Н, где А ⁺ обозначает ядро ​​счетчика на A . Из этого условия нормальности следует, что HA ⁺ является идеалом Хопфа группы H (т. е. идеалом алгебры в ядре коединицы, коидеальной коалгеброй и устойчивой относительно антипода). Как следствие, имеем фактор-алгебру Хопфа H / HA ⁺ и эпиморфизм H → H / A ⁺ H , теория, аналогичная теории нормальных подгрупп и факторгрупп в теории групп .

Хопф приказывает

Порядок Хопфа O над областью целостности R с полем частных K — это порядок в алгебре Хопфа H над K , замкнутый относительно операций алгебры и коалгебры: в частности, коумножение ∆ отображает O в O ⊗ O .

Групповые элементы

Групповой элемент — это ненулевой элемент x такой, что ∆( x ) = x ⊗ x . Групповые элементы образуют группу с обратным антиподом. Примитивный элемент x удовлетворяет условию Δ( x ) = x ⊗1 + 1⊗ x .

Примеры

	В зависимости от	коумножение	Граф	Антипод	коммутативный	Кокоммутативный	Примечания
групповая алгебра КГ	группа G	Δ( g ) = g ⊗ g для всех g в G	ε ( g ) = 1 для всех g в G	S ( г ) знак равно г −1 для всех g в G	тогда и только тогда, когда G абелева	да
функции f из конечного группа к K , K Г (с поточечным сложением и умножением)	конечная группа G	Δ( ж )( Икс , y ) знак равно ж ( ху )	ε ( ж ) знак равно ж (1 г )	S ( ж )( Икс ) знак равно ж ( Икс −1 )	да	тогда и только тогда, когда G абелева
Представительские функции в компактной группе	компактная группа G	Δ( ж )( Икс , y ) знак равно ж ( ху )	ε ( ж ) знак равно ж (1 г )	S ( ж )( Икс ) знак равно ж ( Икс −1 )	да	тогда и только тогда, когда G абелева	И наоборот, каждая коммутативная инволютивная приведенная алгебра Хопфа над C с конечным интегралом Хаара возникает таким образом, давая одну формулировку двойственности Таннаки–Крейна .
Регулярные функции на алгебраической группе		Δ( ж )( Икс , y ) знак равно ж ( ху )	ε ( ж ) знак равно ж (1 г )	S ( ж )( Икс ) знак равно ж ( Икс −1 )	да	тогда и только тогда, когда G абелева	И наоборот, каждая коммутативная алгебра Хопфа над полем возникает из групповой схемы таким образом , что дает антиэквивалентность категорий.
Tensor algebra T( V )	векторное пространство V	Δ( x ) знак равно x ⊗ 1 + 1 ⊗ x , x в V , Δ(1) = 1 ⊗ 1	ε ( Икс ) знак равно 0	S ( x ) = − x для всех x в 'T 1 ( V ) (и распространяется на более высокие тензорные степени)	Тогда и только тогда, когда dim( V )=0,1	да	симметрическая алгебра и внешняя алгебра (которые являются факторами тензорной алгебры) также являются алгебрами Хопфа с этим определением коумножения, коединицы и антипода.
Универсальная обертывающая алгебра U(g)	Алгебра Ли g	Δ( x ) = x ⊗ 1 + 1 ⊗ x для каждого x в g (это правило совместимо с коммутаторами и поэтому может быть однозначно распространено на все U )	ε ( x ) = 0 для всех x в g (опять же расширено до U )	S ( Икс ) знак равно - Икс	тогда и только тогда, когда g абелева	да
Алгебра Свидлера Хопфа H = K [ c , x ]/ c 2 = 1, х 2 = 0 и хс = - сх .	K – поле с характеристикой, отличной от 2	Δ( c ) = c ⊗ c , Δ( x ) = c ⊗ x + x ⊗ 1, Δ(1) = 1 ⊗ 1	ε ( c ) знак равно 1 и ε ( Икс ) знак равно 0	S ( с ) знак равно с −1 знак равно c и S ( x ) = - cx	нет	нет	Базовое векторное пространство генерируется {1, c , x , cx } и, следовательно, имеет размерность 4. Это наименьший пример алгебры Хопфа, которая является одновременно некоммутативной и некокоммутативной.
кольцо симметричных функций		в терминах полных однородных симметричных функций h k ( k ≥ 1): Δ( час k ) знак равно 1 ⊗ час k + час 1 ⊗ час k -1 + ... + час k -1 ⊗ час 1 + час k ⊗ 1.	ε ( час k ) знак равно 0	S ( час k ) знак равно (−1) к я к	да	да

Обратите внимание, что функции в конечной группе можно отождествить с групповым кольцом, хотя их более естественно считать двойственными - групповое кольцо состоит из конечных сумм элементов и, таким образом, соединяется с функциями в группе путем вычисления функции на суммированном элементы.

Когомологии групп Ли

Алгебра когомологий (над полем $K$) группы Ли $G$ является алгеброй Хопфа: умножение обеспечивается произведением чашки , а коумножение

$H^{*}(G,K)\rightarrow H^{*}(G\times G,K)\cong H^{*}(G,K)\otimes H^{*}(G,K)$

групповым умножением $G\times G\to G$. Это наблюдение фактически послужило источником понятия алгебры Хопфа. Используя эту структуру, Хопф доказал структурную теорему для алгебры когомологий групп Ли.

Теорема (Хопфа) Позволять $A$ — конечномерная градуированная коммутативная градуированная кокоммутативная алгебра Хопфа над полем характеристики 0. Тогда $A$ (как алгебра) — свободная внешняя алгебра с образующими нечетной степени.

Квантовые группы и некоммутативная геометрия

Основная статья: квантовая группа

Большинство приведенных выше примеров либо коммутативны (т. е. умножение коммутативно ), либо кокоммутативны (т. е. Δ = T ∘ Δ, где отображение твиста T : H ⊗ H → H ⊗ H определяется как T ( x ⊗ y ) = y ⊗ x ). Другими интересными алгебрами Хопфа являются некоторые «деформации» или « квантования » алгебр из примера 3, которые не являются ни коммутативными, ни кокоммутативными. Эти алгебры Хопфа часто называют квантовыми группами — термин, который до сих пор имеет лишь слабое определение. Они важны в некоммутативной геометрии , идея в следующем: стандартная алгебраическая группа хорошо описывается ее стандартной алгеброй Хопфа регулярных функций; тогда мы можем думать о деформированной версии этой алгебры Хопфа как описывающей некую «нестандартную» или «квантованную» алгебраическую группу (которая вообще не является алгебраической группой). Хотя, похоже, не существует прямого способа определения этих нестандартных объектов или манипулирования ими, все же можно работать с их алгебрами Хопфа и действительно отождествлять их с их алгебрами Хопфа. Отсюда и название «квантовая группа».

Теория представлений

Пусть A — алгебра Хопфа, M и N — A -модули. Тогда M ⊗ N также является A -модулем, причем

$a(m\otimes n):=\Delta (a)(m\otimes n)=(a_{1}\otimes a_{2})(m\otimes n)=(a_{1}m\otimes a_{2}n)$

для m ∈ M , n ∈ N ∆( ) = ( a1 _и , a2 _a ). Более того, мы можем определить тривиальное представление как базовое поле K с

$a(m):=\epsilon (a)m$

для м € К. ​ двойственное представление А Наконец, можно определить : если М — А -модуль и М* — его двойственное пространство, то

$(af)(m):=f(S(a)m)$

где f ∈ * и m ∈ M. M

Связь между ∆, ε и S гарантирует, что некоторые естественные гомоморфизмы векторных пространств действительно являются гомоморфизмами A -модулей. Например, естественные изоморфизмы векторных пространств M → M ⊗ K и M → K ⊗ M также являются изоморфизмами A -модулей. Кроме того, отображение векторных пространств M* ⊗ M → K с f ⊗ m → f ( m ) также является гомоморфизмом A -модулей. Однако отображение M ⊗ M* → K не обязательно является гомоморфизмом A -модулей.

Связанные понятия

Градуированные алгебры Хопфа часто используются в алгебраической топологии : они представляют собой естественную алгебраическую структуру прямой суммы всех гомологий или когомологий групп H-пространства .

Локально компактные квантовые группы обобщают алгебры Хопфа и несут топологию . Алгебра всех непрерывных функций на группе Ли является локально компактной квантовой группой.

Квази-алгебры Хопфа являются обобщениями алгебр Хопфа, где коассоциативность сохраняется только до поворота. Они использовались при исследовании уравнений Книжника–Замолодчикова .

Мультипликативные алгебры Хопфа, введенные Альфонсом Ван Даэлем в 1994 году. являются обобщениями алгебр Хопфа , где коумножение алгебры (с единицей или без нее) на алгебру мультипликатора алгебры тензорного произведения алгебры с самой собой.

Групповые (ко)алгебры Хопфа, введенные В. Г. Тураевым в 2000 г., также являются обобщениями алгебр Хопфа.

Слабые алгебры Хопфа

Слабые алгебры Хопфа , или квантовые группоиды, являются обобщениями алгебр Хопфа. Как и алгебры Хопфа, слабые алгебры Хопфа образуют самодвойственный класс алгебр; т. е. если H является (слабой) алгеброй Хопфа, то же самое относится и к H *, двойственному пространству линейных форм к H (относительно структуры алгебра-коалгебры, полученной в результате естественного спаривания с H и ее структуры коалгебра-алгебра). Слабой алгеброй Хопфа H обычно считается

• конечномерная алгебра и коалгебра с копроизведением ∆: H → H ⊗ H и единицей ε: H → k, удовлетворяющим всем аксиомам алгебры Хопфа, кроме, возможно, ∆(1) ≠ 1 ⊗ 1 или ε( ab ) ≠ ε( a )ε ( b для некоторых a,b в H. ) Вместо этого требуется следующее:

$(\Delta (1)\otimes 1)(1\otimes \Delta (1))=(1\otimes \Delta (1))(\Delta (1)\otimes 1)=(\Delta \otimes {\mbox{Id}})\Delta (1)$

$\epsilon (abc)=\sum \epsilon (ab_{(1)})\epsilon (b_{(2)}c)=\sum \epsilon (ab_{(2)})\epsilon (b_{(1)}c)$

для a , b и c в H. всех

• H имеет ослабленный антипод S : H → H, удовлетворяющий аксиомам:

1. $S(a_{(1)})a_{(2)}=1_{(1)}\epsilon (a1_{(2)})$ для всех a из H (правая часть представляет собой интересный проектор, обычно обозначаемый Π ^Р ( a ) или ε _s ( a ) с образом сепарабельной подалгебры, обозначаемой H ^Р или Hs ₎ ;
2. $a_{(1)}S(a_{(2)})=\epsilon (1_{(1)}a)1_{(2)}$ для всех a из H (еще один интересный проектор, обычно обозначаемый Π ^Р ( a ) или ε _t ( a ) с образом сепарабельной алгебры H ^л или H _t , антиизоморфный H ^л через S );
3. $S(a_{(1)})a_{(2)}S(a_{(3)})=S(a)$ для a в H. всех

Заметим, что если ∆(1) = 1 ⊗ 1, эти условия сводятся к двум обычным условиям на антипод алгебры Хопфа.

Аксиомы частично выбраны так, что категория H -модулей является жесткой моноидальной категорией . Единичным H -модулем является сепарабельная алгебра H ^л упомянуто выше.

Например, конечная группоидная алгебра является слабой алгеброй Хопфа. , группоидная алгебра на [n] с одной парой обратимых стрелок и _{частности} eji между _в i и j eij [ n ] изоморфна алгебре H матриц n x В n . Структура слабой алгебры Хопфа на этом конкретном H задается копроизведением Δ( e _ij ) = e _ij ⊗ e _ij , единицей ε( e _ij ) = 1 и антиподом S ( e _ij ) = e _ji . Сепарабельные подалгебры H ^л и Х ^Р совпадают и в данном конкретном случае являются нецентральными коммутативными алгебрами (подалгеброй диагональных матриц).

Ранние теоретические вклады в слабые алгебры Хопфа можно найти в а также

Алгеброиды Хопфа

См . алгеброид Хопфа.

Аналогия с группами

Группы могут быть аксиоматизированы с помощью тех же диаграмм (эквивалентно операциям), что и алгебра Хопфа, где G рассматривается как множество, а не как модуль. В этом случае:

• поле K заменяется одноточечным множеством
• есть натуральная единица (отобразить до 1 точки)
• существует естественное умножение (диагональное отображение)
• единица является идентификационным элементом группы
• умножение - это умножение в группе
• антипод - это обратная сторона

В этой философии группу можно рассматривать как алгебру Хопфа над « полем с одним элементом ».

Алгебры Хопфа в сплетенных моноидальных категориях

Определение алгебры Хопфа естественным образом распространяется на произвольные сплетенные моноидальные категории . Алгебра Хопфа в такой категории $(C,\otimes ,I,\alpha ,\lambda ,\rho ,\gamma )$ шестикратный $(H,\nabla ,\eta ,\Delta ,\varepsilon ,S)$ где $H$ является объектом в $C$, и

$\nabla :H\otimes H\to H$ (умножение),

$\eta :I\to H$ (единица),

$\Delta :H\to H\otimes H$ (умножение),

$\varepsilon :H\to I$ (единица),

$S:H\to H$ (антипод)

— являются морфизмами в $C$ такой, что

1) тройка $(H,\nabla ,\eta )$ является моноидом в моноидальной категории $(C,\otimes ,I,\alpha ,\lambda ,\rho ,\gamma )$, т.е. следующие диаграммы коммутативны:

2) тройка $(H,\Delta ,\varepsilon )$ является комоноидом моноидальной категории $(C,\otimes ,I,\alpha ,\lambda ,\rho ,\gamma )$, т.е. следующие диаграммы коммутативны:

3) структуры моноида и комоноида на $H$ совместимы: умножение $\nabla$ и единица $\eta$ являются морфизмами комоноидов, и (что эквивалентно в данной ситуации) одновременно коумножение $\Delta$ и единица $\varepsilon$ являются морфизмами моноидов; это означает, что следующие диаграммы должны быть коммутативными:

где $\lambda _{I}:I\otimes I\to I$ — левый единичный морфизм в $C$, и $\theta$ естественное преобразование функторов $(A\otimes B)\otimes (C\otimes D){\stackrel {\theta }{\rightarrowtail }}(A\otimes C)\otimes (B\otimes D)$ единственное в классе естественных преобразований функторов, составленных из структурных преобразований (ассоциативности, левых и правых единиц, транспозиции и их обратных) в категории $C$.

Пятерка $(H,\nabla ,\eta ,\Delta ,\varepsilon )$ со свойствами 1),2),3) называется биалгеброй в категории $(C,\otimes ,I,\alpha ,\lambda ,\rho ,\gamma )$;

4) диаграмма антипода коммутативна:

Типичными примерами являются следующие.

• Группы . В моноидальной категории $({\text{Set}},\times ,1)$ множеств ( с декартовым произведением $\times$ как тензорное произведение и произвольный однотон, скажем, $1=\{\varnothing \}$, как единичный объект) тройка $(H,\nabla ,\eta )$ является моноидом в категориальном смысле тогда и только тогда, когда он является моноидом в обычном алгебраическом смысле , т. е. если выполняются операции $\nabla (x,y)=x\cdot y$ и $\eta (1)$ ведут себя как обычное умножение и единица в $H$ (но возможно без обратимости элементов $x\in H$). В то же время тройка $(H,\Delta ,\varepsilon )$ является комоноидом в категориальном смысле тогда и только тогда, когда $\Delta$ диагональная операция $\Delta (x)=(x,x)$ (и операция $\varepsilon$ также определяется однозначно: $\varepsilon (x)=\varnothing$). И любая такая структура комоноида $(H,\Delta ,\varepsilon )$ совместим с любой структурой моноида $(H,\nabla ,\eta )$ в том смысле, что диаграммы из п. 3 определения всегда коммутируют. Как следствие, каждый моноид $(H,\nabla ,\eta )$ в $({\text{Set}},\times ,1)$ естественно можно рассматривать как биалгебру $(H,\nabla ,\eta ,\Delta ,\varepsilon )$ в $({\text{Set}},\times ,1)$, и наоборот. Существование антипода $S:H\to H$ для такой биалгебры $(H,\nabla ,\eta ,\Delta ,\varepsilon )$ означает именно то, что каждый элемент $x\in H$ имеет обратный элемент $x^{-1}\in H$ относительно умножения $\nabla (x,y)=x\cdot y$. Таким образом, в категории множеств $({\text{Set}},\times ,1)$ Алгебры Хопфа — это в точности группы в обычном алгебраическом смысле.
• Классические алгебры Хопфа . В частном случае, когда $(C,\otimes ,s,I)$ это категория векторных пространств над заданным полем $K$, алгебры Хопфа в $(C,\otimes ,s,I)$ являются в точности классическими алгебрами Хопфа, описанными выше .
• Функциональные алгебры на группах . Стандартные функциональные алгебры ${\mathcal {C}}(G)$, ${\mathcal {E}}(G)$, ${\mathcal {O}}(G)$, ${\mathcal {P}}(G)$ (непрерывных, гладких, голоморфных, регулярных функций) на группах являются алгебрами Хопфа в категории ( Ste , $\odot$) стереотипных пространств ,
• Групповые алгебры . Стереотипные групповые алгебры ${\mathcal {C}}^{\star }(G)$, ${\mathcal {E}}^{\star }(G)$, ${\mathcal {O}}^{\star }(G)$, ${\mathcal {P}}^{\star }(G)$ (мер, распределений, аналитических функционалов и токов) на группах являются алгебрами Хопфа в категории ( Ste , $\circledast$) стереотипных пространств . Эти алгебры Хопфа используются в теориях двойственности некоммутативных групп .

См. также

• Квазитреугольная алгебра Хопфа
• Алгебра/аналогия множеств
• Теория представлений алгебр Хопфа
• Ленточная алгебра Хопфа
• Супералгебра
• Супергруппа
• Любая алгебра Ли
• Алгебра Свидлера Хопфа
• Алгебра перестановок Хопфа
• Теорема Милнора – Мура

Примечания и ссылки

Ссылки

• Даскалеску, Сорин; Нэстасеску, Константин; Райану, Шербан (2001), Алгебра Хопфа. Введение , Чистая и прикладная математика, том 235 (1-е изд.), Марсель Деккер, ISBN.  978-0-8247-0481-0 , Збл   0962.16026 .
• Картье, Пьер (2007), «Букварь по алгебрам Хопфа», в Картье, П.; Мусса, П.; Юлия, Б.; Ванхов, П. (ред.), Границы теории чисел, физики и геометрии , том. II, Берлин: Springer, стр. 537–615, номер документа : 10.1007/978-3-540-30308-4_12 , ISBN.  978-3-540-30307-7
• Фукс, Юрген (1992), Аффинные алгебры Ли и квантовые группы. Введение с приложениями в конформную теорию поля , Кембриджские монографии по математической физике, Кембридж: Cambridge University Press, ISBN  978-0-521-48412-1 , Збл   0925.17031
• Хайнц Хопф , О топологии групповых многообразий и их обобщениях, Annals of Mathematics 42 (1941), 22–52. Перепечатано в Selecta Heinz Hopf, стр. 119–151, Springer, Берлин (1964). МИСТЕР 4784 , Збл   0025.09303
• Монтгомери, Сьюзен (1993), Алгебры Хопфа и их действия на кольцах , Серия региональных конференций по математике, том. 82, Провиденс, Род-Айленд: Американское математическое общество , ISBN  978-0-8218-0738-5 , Збл   0793.16029
• Стрит, Росс (2007), Квантовые группы: путь к современной алгебре , Серия лекций Австралийского математического общества, том. 19, Издательство Кембриджского университета, ISBN  978-0-521-69524-4 , МР   2294803 , Збл   1117.16031 .
• Свидлер, Мосс Э. (1969), Алгебры Хопфа , Серия лекций по математике, WA Benjamin, Inc., Нью-Йорк, ISBN  9780805392548 , МР   0252485 , Збл   0194.32901
• Андервуд, Роберт Г. (2011), Введение в алгебры Хопфа , Берлин: Springer-Verlag, ISBN  978-0-387-72765-3 , Збл   1234.16022
• Тураев Владимир; Вирелизье, Алексис (2017), Моноидальные категории и топологическая теория поля , Progress in Mathematics, vol. 322, Спрингер, номер домена : 10.1007/978-3-319-49834-8 , ISBN.  978-3-319-49833-1 .
• Акбаров, С.С. (2003). «Двойственность Понтрягина в теории топологических векторных пространств и в топологической алгебре» . Журнал математических наук . 113 (2): 179–349. дои : 10.1023/А:1020929201133 . S2CID   115297067 .
• Акбаров, СС (2009). «Голоморфные функции экспоненциального типа и двойственности для групп Штейна с алгебраической связной составляющей единицы». Журнал математических наук . 162 (4): 459–586. arXiv : 0806.3205 . дои : 10.1007/s10958-009-9646-1 . S2CID   115153766 .