База Грёбнер

В математике , и, более конкретно, в компьютерной алгебре , вычислительной алгебраической геометрии и вычислительной коммутативной алгебре , базис Грёбнера — это особый вид порождающего набора идеала в кольце многочленов K [ x ₁ , ..., x _n ] над поле К. ​ многие важные свойства идеала и связанного с ним алгебраического многообразия Базис Грёбнера позволяет легко вывести , такие как размерность и количество нулей, когда оно конечно. Вычисление в базисе Грёбнера — один из основных практических инструментов решения систем полиномиальных уравнений и вычисления образов алгебраических многообразий при проекциях или рациональных отображениях .

Вычисление базиса Грёбнера можно рассматривать как многомерное нелинейное обобщение как алгоритма Евклида для вычисления полиномиальных наибольших общих делителей , так и Метод исключения Гаусса для линейных систем.

Базы Грёбнера были представлены Бруно Бухбергером в его докторской диссертации 1965 года. диссертация, которая также включала алгоритм их вычисления ( алгоритм Бухбергера ). Он назвал их в честь своего советника Вольфганга Грёбнера . В 2007 году Бухбергер получил Ассоциации вычислительной техники от за эту работу премию Парижа Канеллакиса в области теории и практики .Однако русский математик Николай Гюнтер ввел подобное понятие в 1913 году и опубликовал его в различных российских математических журналах. Эти статьи в значительной степени игнорировались математическим сообществом до их повторного открытия в 1987 году Бодо Реншухом и др. Аналогичная концепция многомерных степенных рядов была независимо разработана Хейсуке Хиронакой в ​​1964 году, который назвал их стандартными базисами . Некоторые авторы использовали этот термин для обозначения базисов Грёбнера.

Теория базисов Грёбнера развивалась многими авторами в различных направлениях. Он был обобщен на другие структуры, такие как многочлены над кольцами главных идеалов или кольцами многочленов , а также на некоторые классы некоммутативных колец и алгебр, таких как алгебры Оре .

Инструменты

Полиномиальное кольцо

Основная статья: Полиномиальное кольцо

Базисы Грёбнера в первую очередь определяются для идеалов в кольце полиномов. $R=K[x_{1},\ldots ,x_{n}]$ над полем К. ​Хотя теория работает для любого поля, большинство вычислений по базису Грёбнера выполняются либо тогда, когда K является полем рациональных чисел , либо целыми числами по модулю простого числа.

В контексте базисов Грёбнера ненулевой многочлен от $R=K[x_{1},\ldots ,x_{n}]$ обычно представляется в виде суммы $c_{1}M_{1}+\cdots +c_{m}M_{m},$ где $c_{i}$ являются ненулевыми элементами K , называемыми коэффициентами , а $M_{i}$ являются мономами (названными Бухбергером и некоторыми его последователями степенными произведениями ) вида $x_{1}^{a_{1}}\cdots x_{n}^{a_{n}},$ где $a_{i}$ являются неотрицательными целыми числами. Вектор $A=[a_{1},\ldots ,a_{n}]$ называется вектором показателя монома. Когда список $X=[x_{1},\ldots ,x_{n}]$ переменных фиксировано, обозначения мономов часто сокращают как $x_{1}^{a_{1}}\cdots x_{n}^{a_{n}}=X^{A}.$

Мономы однозначно определяются своими векторами экспоненты, и, когда мономиальный порядок (см. ниже) фиксирован, полином однозначно представляется упорядоченным списком упорядоченных пар, образованных вектором экспоненты и соответствующим коэффициентом. Такое представление полиномов особенно эффективно для вычислений на основе базиса Грёбнера в компьютерах, хотя оно менее удобно для других вычислений, таких как разложение полинома на факторизацию и определение наибольшего общего делителя полинома .

Если $F=\{f_{1},\ldots ,f_{k}\}$ — конечное множество многочленов в кольце многочленов R , идеал, порождённый F, — это множество линейных комбинаций элементов из F с коэффициентами из R ; это набор многочленов, которые можно записать ${\textstyle \sum _{i=1}^{k}g_{i}f_{i}}$ с $g_{1},\ldots ,g_{k}\in R.$

Мономиальный порядок

Основная статья: Мономиальный порядок

Все операции, связанные с базисами Грёбнера, требуют выбора полного порядка мономов со следующими свойствами совместимости с умножением. Для всех мономов M , N , P ,

1. $M\leq N\Longleftrightarrow MP\leq NP$
2. $M\leq MP$.

Полный порядок, удовлетворяющий этим условиям, иногда называют допустимым порядком .

Эти условия подразумевают, что порядок является хорошим порядком , то есть каждая строго убывающая последовательность мономов конечна.

Хотя базисная теория Грёбнера не зависит от конкретного выбора допустимого мономиального порядка, для приложений особенно важны три мономиальных порядка:

• Лексикографическое упорядочение , обычно называемое lex или plex (для чистого лексического упорядочения).
• Полная степень обратного лексикографического упорядочения , обычно называемая дегревлексом .
• Порядок исключения , lexdeg .

Базисная теория Грёбнера была первоначально введена для лексикографического упорядочения. Вскоре стало понятно, что базис Грёбнера для дегревлекса почти всегда гораздо проще вычислить, и что почти всегда легче вычислить базис Грёбнера, сначала вычислив базис дегревлекса, а затем используя «алгоритм изменения порядка». Когда необходимо устранение , дегревлекс неудобен; можно использовать и lex, и lexdeg, но, опять же, многие вычисления относительно просты с lexdeg и практически невозможны с lex.

Основные операции

, коэффициент и

Как только мономиальный порядок фиксирован, члены многочлена (произведение монома с его ненулевым коэффициентом) естественным образом упорядочиваются по убыванию мономов (для этого порядка). Это делает представление многочлена в виде отсортированного списка пар коэффициент-вектор экспоненты каноническим представлением многочленов (то есть два многочлена равны тогда и только тогда, когда они имеют одинаковое представление).

Первый (наибольший) член многочлена p для этого порядка и соответствующие моном и коэффициент называются соответственно старшим членом , старшим мономом и старшим коэффициентом и обозначаются в этой статье lt( p ), lm( p ) и lc( п ) .

Большинство полиномиальных операций, связанных с базисами Грёбнера, включают ведущие члены. Итак, представление полиномов в виде отсортированных списков делает эти операции особенно эффективными (чтение первого элемента списка занимает постоянное время, независимо от длины списка).

Полиномиальные операции

Другие полиномиальные операции, используемые в базисных вычислениях Грёбнера, также совместимы с мономиальным порядком; то есть их можно выполнить без изменения порядка результата:

• Добавление двух многочленов заключается в слиянии двух соответствующих списков терминов с особым подходом в случае конфликта (то есть, когда один и тот же моном появляется в двух многочленах).
• Умножение многочлена на скаляр состоит из умножения каждого коэффициента на этот скаляр без какого-либо другого изменения представления.
• Умножение многочлена на моном m состоит из умножения каждого монома многочлена на m . Это не меняет термин «упорядочение» по определению мономиального порядка.

Делимость одночленов

Позволять $M=x_{1}^{a_{1}}\cdots x_{n}^{a_{n}}$ и $N=x_{1}^{b_{1}}\cdots x_{n}^{b_{n}}$ быть двумя мономами с векторами показателей $A=[a_{1},\ldots ,a_{n}]$ и $B=[b_{1},\ldots ,b_{n}].$

Говорят, что N или что N кратно M M , делит если $a_{i}\leq b_{i}$ для каждого я ; то есть, если A покомпонентно не больше, чем B . В этом случае частное ${\textstyle {\frac {N}{M}}}$ определяется как ${\textstyle {\frac {N}{M}}=x_{1}^{b_{1}-a_{1}}\cdots x_{n}^{b_{n}-a_{n}}.}$ Другими словами, вектор экспоненты ${\textstyle {\frac {N}{M}}}$ является покомпонентным вычитанием векторов экспонент N и M .

Наибольший общий делитель НОД( M , N ) чисел M и N — это моном ${\textstyle x_{1}^{\min(a_{1},b_{1})}\cdots x_{n}^{\min(a_{n},b_{n})}}$ чей вектор экспоненты является покомпонентным минимумом A и B . Наименьшее общее кратное lcm( M , N ) определяется аналогично с max вместо min .

У одного есть

$\operatorname {lcm} (M,N)={\frac {MN}{\gcd(M,N)}}.$

Сокращение

Сокращение полинома другими полиномами относительно мономиального порядка занимает центральное место в теории базиса Грёбнера. Это обобщение сокращения строк, происходящего на этапах исключения по Гауссу и деления. Евклидово деление одномерных многочленов . Когда оно выполнено в максимально возможной степени, его иногда называют многомерным делением , хотя его результат не определен однозначно.

Сокращение свинца — это особый случай сокращения, который легче вычислить. Это имеет фундаментальное значение для вычисления базиса Грёбнера, поскольку общая редукция необходима только в конце вычисления базиса Грёбнера, чтобы получить уменьшенный базис Грёбнера из нередуцированного.

Пусть фиксирован допустимый мономиальный порядок, к которому относится каждое мономиальное сравнение, которое будет происходить в этом разделе.

Многочлен f можно привести к другому многочлену g , если ведущий моном lm( f ) кратен lm( g ) . Многочлен f можно сократить с помощью g , если некоторый моном f кратен lm( g ) . (Итак, если f приводимо к свинцу с помощью g , оно также приводимо, но f может быть приводимо, не будучи приводимым при помощи свинца.)

Предположим, что f можно сократить с помощью g , и пусть cm — такой член f , что моном m кратен lm( g ) . Одношаговое уменьшение f g на замене состоит в f на

$\operatorname {red} _{1}(f,g)=f-{\frac {c}{\operatorname {lc} (g)}}\,{\frac {m}{\operatorname {lm} (g)}}\,g.$

Эта операция удаляет моном m из f без изменения членов с мономом, большим, чем m (для мономиального порядка). В частности, одношаговое сокращение f f все мономы которого меньше lm( дает полином , ) .

Учитывая конечное множество G полиномов, говорят, что f приводимо если или свинцово приводимо с помощью G, оно приводимо или свинцово приводимо соответственно по крайней мере к одному элементу g из G . В этом случае одношаговое уменьшение (соответственно одношаговое уменьшение опережения) f с помощью G представляет собой любое одношаговое уменьшение (соответственно одношаговое уменьшение опережения) f элементом G .

(Полное) сокращение (соответственно сокращение свинца) f с помощью G состоит из итераций одношаговых сокращений (с уважением к одношаговым сокращениям свинца) до тех пор, пока не будет получен полином, который является неприводимым (соответственно свинцово-неприводимым) с помощью G . иногда называет нормальной f формой G его . В общем, эта форма не определена однозначно, поскольку, как правило, существует несколько элементов G , которые можно использовать для уменьшения f ; эта неединственность является отправной точкой базисной теории Грёбнера.

Определение редукции сразу показывает, что если h является нормальной формой f по G , то имеет место

$f=h+\sum _{g\in G}q_{g}\,g,$

где h неприводим с помощью G и $q_{g}$ являются полиномами такими, что $\operatorname {lm} (q_{g}\,g)\leq \operatorname {lm} (f).$ В случае одномерных многочленов, если G одного элемента g , то h — это остаток евклидова деления f на g состоит из , а q _g — частное. Более того, алгоритм деления — это именно процесс сокращения лидов. По этой причине некоторые авторы используют термин многомерное деление вместо редукции.

Неуникальность редукции

В следующем примере есть ровно два полных сокращения свинца, которые дают два совершенно разных результата. Тот факт, что результаты неприводимы (не только свинцово-неприводимые), специфичен для данного примера, хотя это довольно часто встречается в таких небольших примерах.

В этом примере с двумя переменными используется мономиальный порядок — это лексикографический порядок с $x>y,$ и мы рассматриваем сокращение $f=2x^{3}-x^{2}y+y^{3}+3y$, к $G=\{g_{1},g_{2}\},$ с

$${\begin{aligned}g_{1}&=x^{2}+y^{2}-1,\\g_{2}&=xy-2.\end{aligned}}$$

На первом этапе сокращения либо первый, либо второй член f может быть уменьшен. Однако сокращение срока равнозначно удалению этого срока за счет добавления новых более низких сроков; если сокращается не первый сокращаемый член, то может случиться так, что дальнейшее сокращение добавит аналогичный член, который придется сокращать снова. Поэтому всегда лучше сначала уменьшить наибольший (для мономиального порядка) приводимый член; то есть, в частности, сначала провести сокращение свинца, пока не будет получен неприводимый к свинцу полином.

Ведущий термин $2x^{3}$ из f сокращается на $g_{1}$ и не по $g_{2}.$ Итак, первый шаг сокращения состоит из умножения $g_{1}$ на –2 x и добавив результат к f :

$f\;\xrightarrow {-2xg_{1}} \;f_{1}=f-2xg_{1}=-x^{2}y-2xy^{2}+2x+y^{3}+3y.$

Ведущий термин $-x^{2}y$ из $f_{1}$ кратно ведущим мономам обоих $g_{1}$ и $g_{2},$ Таким образом, у нас есть два варианта второго шага сокращения. Если кто-то выбирает $g_{2},$ получается полином, который можно снова уменьшить на $g_{2}\colon$

$f\;\xrightarrow {-2xg_{1}} \;f_{1}\;\xrightarrow {xg_{2}} \;-2xy^{2}+y^{3}+3y\;\xrightarrow {2yg_{2}} \;f_{2}=y^{3}-y.$

Дальнейшее сокращение невозможно, поэтому $f_{2}$ является полной редукцией f .

Один получает другой результат при другом выборе для второго шага:

$f\;\xrightarrow {-2xg_{1}} \;f_{1}\;\xrightarrow {yg_{1}} \;-2xy^{2}+2x+2y^{3}+2y\;\xrightarrow {2yg_{2}} \;f_{3}=2x+2y^{3}-2y.$

И снова результат $f_{3}$ не подлежит сокращению, хотя было сделано только сокращение содержания свинца.

Таким образом, полное уменьшение f может привести либо к $f_{2}=y^{3}-y$ или $f_{3}=2x+2y^{3}-2y.$

Именно для решения проблем, возникающих из-за этой неединственности, Бухбергер ввел базисы Грёбнера и S -полиномы. Интуитивно, 0 = f − f можно свести к $f_{2}-f_{3}.$ Это подразумевает, что $f_{2}-f_{3}$ принадлежит идеалу, порожденному G . Итак, этот идеал не меняется добавлением $f_{3}-f_{2}$ до G , и это позволяет сделать больше сокращений. В частности, $f_{3}$ можно свести к $f_{2}$ к $f_{3}-f_{2}$ и это восстанавливает уникальность приведенной формы.

Здесь алгоритм Бухбергера для базисов Грёбнера начинается с добавления к G полинома

$g_{3}=yg_{1}-xg_{2}=2x+y^{3}-y.$

Этот многочлен, названный Бухбергером S -полиномиалом, представляет собой разность одношаговых сокращений наименьшего общего кратного. $x^{2}y$ из ведущих мономов $g_{1}$ и $g_{2}$, к $g_{2}$ и $g_{1}$ соответственно:

$g_{3}=\left(x^{2}y-{\frac {x^{2}y}{lt(g_{2})}}g_{2}\right)-\left(x^{2}y-{\frac {x^{2}y}{lt(g_{1})}}g_{1}\right)={\frac {x^{2}y}{lt(g_{1})}}g_{1}-{\frac {x^{2}y}{lt(g_{2})}}g_{2}$.

В этом примере имеется $g_{3}=f_{3}-f_{2}.$ Это не завершает алгоритм Бухбергера, поскольку xy дает разные результаты при уменьшении на $g_{2}$ или $g_{3}.$

S -полином

При мономиальном порядке S-полином или критическая пара двух многочленов f и g представляет собой многочлен

$S(f,g)=\operatorname {red} _{1}(\mathrm {lcm} ,g)-\operatorname {red} _{1}(\mathrm {lcm} ,f)$;

где lcm обозначает наименьшее общее кратное ведущих мономов f и g .Используя определение $\operatorname {red} _{1}$, это переводится как:

${\begin{aligned}S(f,g)&=\left(\mathrm {lcm} -{\frac {1}{\operatorname {lc} (g)}}\,{\frac {\mathrm {lcm} }{\operatorname {lm} (g)}}\,g\right)-\left(\mathrm {lcm} -{\frac {1}{\operatorname {lc} (f)}}\,{\frac {\mathrm {lcm} }{\operatorname {lm} (f)}}\,f\right)\\&={\frac {1}{\operatorname {lc} (f)}}\,{\frac {\mathrm {lcm} }{\operatorname {lm} (f)}}\,f-{\frac {1}{\operatorname {lc} (g)}}\,{\frac {\mathrm {lcm} }{\operatorname {lm} (g)}}\,g\\\end{aligned}}.$

Используя свойство, связывающее lcm и gcd , S -полиномиал также можно записать как:

$S(f,g)={\frac {1}{\operatorname {lc} (f)}}\,{\frac {\operatorname {lm} (g)}{\mathrm {gcd} }}\,f-{\frac {1}{\operatorname {lc} (g)}}\,{\frac {\operatorname {lm} (f)}{\mathrm {gcd} }}\,g;$

где gcd обозначает наибольший общий делитель старших мономов f и g .

Поскольку мономы, которые можно сократить как с помощью f, так и с помощью g , в точности кратны lcm , можно справиться со всеми случаями неединственности приведения, рассматривая только S -полиномы. Это фундаментальный факт для теории базиса Грёбнера и всех алгоритмов их вычисления.

Чтобы избежать дробей при работе с полиномами с целыми коэффициентами, полином S часто определяется как

$S(f,g)=\operatorname {lc} (g)\,{\frac {\operatorname {lm} (g)}{\mathrm {gcd} }}\,f-\operatorname {lc} (f),{\frac {\operatorname {lm} (f)}{\mathrm {gcd} }}\,g;$

Это ничего не меняет в теории, поскольку два полинома являются ассоциированными .

Определение

Позволять $R=F[x_{1},\ldots ,x_{n}]$ — кольцо полиномов над полем F . В этом разделе мы предполагаем, что допустимый мономиальный порядок зафиксирован.

Пусть G конечное множество полиномов R , порождающее идеал I. — из Множество G является базисом Грёбнера (относительно мономиального порядка) или, точнее, базисом Грёбнера I , если

1. идеал, порожденный ведущими мономами многочленов из I, равен идеалу, порожденному ведущими мономами из G ,

или, что то же самое,

2. старший моном каждого многочлена из I кратен старшему моному некоторого многочлена из G .

Существует множество характеризующих свойств, каждое из которых можно рассматривать как эквивалентное определение базисов Грёбнера. Для краткости в следующем списке обозначение «одно слово/другое слово» означает, что можно взять либо «одно слово», либо «другое слово» за наличие двух разных характеристик базисов Грёбнера. Все следующие утверждения являются характеризациями базисов Грёбнера:

3. многочлен f находится в I тогда и только тогда, когда некоторая/каждая полная редукция/редукция f с помощью G дает нулевой полином;
4. для каждого S -полинома s элементов G некоторое/каждое полное сокращение/редукция s с помощью G дает ноль;
5. все полные сокращения элемента R дают один и тот же результат;
6. мономы, неприводимые G, образуют базис F -векторного пространства $R/I.$

С учетом приведенного выше определения это дает 12 характеристик базисов Грёбнера. Тот факт, что возможно так много характеризаций, делает базисы Грёбнера очень полезными. Например, условие 3 предоставляет алгоритм проверки идеального членства ; условие 4 обеспечивает алгоритм проверки того, является ли набор полиномов базисом Грёбнера, и составляет основу алгоритма Бухбергера для вычисления базисов Грёбнера; условия 5 и 6 позволяют проводить вычисления в $R/I$ способом, который очень похож на модульную арифметику .

Существование

Для любого допустимого мономиального порядка и любого конечного множества G многочленов существует базис Грёбнера, содержащий G и порождающий тот же идеал. Более того, такой базис Грёбнера можно вычислить с помощью алгоритма Бухбергера .

Этот алгоритм использует условие 4 и действует примерно следующим образом: для любых двух элементов G вычислите полное сокращение на G их S -полинома и добавьте результат к G, если он не равен нулю; повторяйте эту операцию с включенными новыми элементами G до тех пор, пока в конечном итоге все сокращения не дадут ноль.

Алгоритм всегда завершается из-за леммы Диксона или из-за того, что кольца многочленов нётеровы ( базисная теорема Гильберта ). Условие 4 гарантирует, что результат является базисом Грёбнера, а определения S -полиномов и редукции гарантируют, что порожденный идеал не изменится.

Вышеописанный метод представляет собой алгоритм вычисления базисов Грёбнера; однако это очень неэффективно. Было предложено и реализовано множество улучшений исходного алгоритма Бухбергера и нескольких других алгоритмов, которые значительно повышают эффективность. См . § Алгоритмы и реализации ниже.

основания

Базис Грёбнера - это минимальна , если все ведущие мономы ее элементов неприводимы к остальным элементам базиса. Учитывая базис Грёбнера идеала I , можно получить минимальный базис Грёбнера I , удалив многочлены, ведущие мономы которых кратны старшему моному другого элемента базиса Грёбнера. Однако если два многочлена базиса имеют один и тот же ведущий моном, удалить нужно только один. Итак, каждый базис Грёбнера содержит в качестве подмножества минимальный базис Грёбнера.

Все минимальные базы Грёбнера данного идеала (при фиксированном мономиальном порядке) имеют одинаковое количество элементов и одинаковые ведущие мономы, а неминимальные базы Грёбнера имеют больше элементов, чем минимальные.

Базис Грёбнера - это уменьшен , если каждый многочлен в нем неприводим к другим элементам базиса и имеет 1 в качестве старшего коэффициента. Итак, каждый приведенный базис Грёбнера минимален, но минимальный базис Грёбнера не обязательно редуцировать.

Учитывая базис Грёбнера идеала I , можно получить уменьшенный базис Грёбнера I , сначала удалив полиномы, которые можно привести с помощью других элементов базиса (для получения минимального базиса); затем замена каждого элемента базиса результатом полной редукции другими элементами базиса; и, наконец, делением каждого элемента базиса на его старший коэффициент.

Все приведенные базисы Грёбнера идеала (при фиксированном мономиальном порядке) равны. Отсюда следует, что два идеала равны тогда и только тогда, когда они имеют один и тот же приведенный базис Грёбнера.

Иногда приведенные базисы Грёбнера определяются без условия на старшие коэффициенты. В этом случае единственность приведенных базисов Грёбнера справедлива лишь с точностью до умножения многочленов на ненулевую константу.

При работе с полиномами по полю $\mathbb {Q}$ из рациональных чисел полезно работать только с многочленами с целыми коэффициентами. В этом случае условие на старшие коэффициенты при определении приведенного базиса можно заменить условием, что все элементы базиса являются примитивными многочленами с целыми коэффициентами, с положительными старшими коэффициентами. Это восстанавливает уникальность сокращенных баз.

Особые случаи

Для любого мономиального порядка пустой набор многочленов является единственным базисом Грёбнера нулевого идеала .

Для любого мономиального порядка набор многочленов, содержащий ненулевую константу, является базисом Грёбнера единичного идеала (всего кольца полиномов). И наоборот, каждый базис Грёбнера единичного идеала содержит ненулевую константу. Приведенный базис Грёбнера единицы формируется одним полиномом 1 .

В случае полиномов от одной переменной существует единственный допустимый мономиальный порядок — порядок по степени. Минимальные базисы Грёбнера — это синглтоны, состоящие из одного многочлена. Приведенные базисы Грёбнера представляют собой монические многочлены .

Пример и контрпример

Нули $f$ сформируйте красную параболу; нули $g$ сформируйте три синие вертикальные линии. Их пересечение состоит из трёх точек.

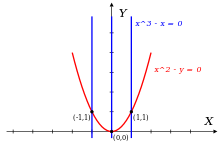
Позволять $R=\mathbb {Q} [x,y]$ — кольцо двумерных многочленов с рациональными коэффициентами и рассмотрим идеал $I=\langle f,g\rangle$ порожденный полиномами

$f=x^{2}-y$,

$g=x^{3}-x$.

Уменьшая g на f , можно получить новый многочлен k такой, что $I=\langle f,k\rangle :$

$k=g-xf=xy-x.$

Ни одно из f и k не может быть сокращено другим, но xk можно сократить с помощью f , что дает еще один полином от I :

$h=xk-(y-1)f=y^{2}-y.$

При лексикографическом упорядочении с $x>y$ у нас есть

lt( ж ) = х ²

lt( k ) = xy

lt( час ) = y ²

Поскольку f , k и h принадлежат I и ни один из них не редуцируем другим, ни один из $\{f,k\},$ $\{f,h\},$ и $\{h,k\}$ является базисом Грёбнера I .

С другой стороны, { f , k , h } является базисом Грёбнера I , поскольку S-полиномы

${\begin{aligned}yf-xk&=y(x^{2}-y)-x(xy-x)=f-h\\yk-xh&=y(xy-x)-x(y^{2}-y)=0\\y^{2}f-x^{2}h&=y(yf-xk)+x(yk-xh)\end{aligned}}$

может быть сведено к нулю с помощью f , k и h .

Метод, который использовался здесь для нахождения h и k и доказательства того, что { f , k , h } является базисом Грёбнера, является прямым применением алгоритма Бухбергера . Таким образом, его можно механически применить к любому подобному примеру, хотя, как правило, необходимо учитывать множество полиномов и S-полиномов, а вычисления, как правило, слишком велики, чтобы их можно было выполнить без компьютера.

базисов

Если не указано иное, все последующие результаты верны для любого мономиального порядка (определения различных порядков, упомянутых ниже, см. в этой статье).

Распространено заблуждение, что для некоторых из этих результатов необходим лексикографический порядок. Напротив, лексикографический порядок почти всегда сложнее всего вычислить, и его использование делает непрактичными многие вычисления, которые относительно просты с помощью градуированного обратного лексикографического порядка (grevlex) или, когда необходимо исключение, порядка исключения (lexdeg ), который ограничивается grevlex для каждого блока переменных.

Равенство идеалов

Приведенные базисы Грёбнера уникальны для любого данного идеала и любого мономиального порядка. Таким образом, два идеала равны тогда и только тогда, когда они имеют один и тот же (редуцированный) базис Грёбнера (обычно программное обеспечение, основанное на базисе Грёбнера, всегда создаёт уменьшенные базисы Грёбнера).

идеалов

Сокращение многочлена f f базисом Грёбнера G идеала I дает 0 тогда и только тогда, когда находится в I . Это позволяет проверить принадлежность элемента идеалу. Другой метод состоит в проверке того, что базис Грёбнера группы G ∪{ f } равен G .

ли идеал I, порожденный f ₁ , ..., f _k, Чтобы проверить, содержится в идеале J , достаточно проверить, что каждый f _I находится в J . Можно также проверить равенство приведенных базисов Грёбнера J и J ∪ { f ₁ , ..., f _k } .

Решения системы алгебраических уравнений

Основная статья: Система полиномиальных уравнений

Любой набор полиномов можно рассматривать как систему полиномиальных уравнений, приравнивая полиномы нулю. Множество решений такой системы зависит только от порожденного идеала и поэтому не меняется при замене данного порождающего набора базисом Грёбнера при любом упорядочении порожденного идеала. Такое решение с координатами в алгебраически замкнутом поле, содержащем коэффициенты многочленов, называется нулем идеала . В обычном случае рациональных коэффициентов это алгебраически замкнутое поле выбирается в качестве комплексного поля .

Идеал не имеет нуля (система уравнений несовместна ) тогда и только тогда, когда 1 принадлежит идеалу (это Nullstellensatz Гильберта ), или, что то же самое, если его базис Грёбнера (для любого мономиального порядка) содержит 1, или, также, если соответствующий приведенный базис Грёбнера равен [1].

Учитывая базис Грёбнера G идеала I , он имеет только конечное число нулей тогда и только тогда, когда для каждой переменной x G в содержит многочлен со старшим мономом, являющимся степенью x (без какой-либо другой переменной, появляющейся ведущий термин). Если это так, то количество нулей, подсчитанных с кратностью, равно количеству мономов, не кратных ни одному ведущему моному группы G . Это число называется степенью идеала.

Когда число нулей конечно, базис Грёбнера для лексикографического мономиального упорядочения теоретически обеспечивает решение: первая координата решения является корнем наибольшего общего делителя полиномов базиса, которые зависят только от первой переменной. После подстановки этого корня в базис вторая координата этого решения является корнем наибольшего общего делителя полученных многочленов, зависящих только от второй переменной, и так далее. Этот процесс решения является только теоретическим, поскольку он предполагает вычисление НОД и поиск корней многочленов с приближенными коэффициентами, что практически невозможно из-за числовой нестабильности. Поэтому были разработаны другие методы решения полиномиальных систем с помощью базисов Грёбнера ( см. В разделе «Система полиномиальных уравнений подробнее »).

, степень и

Размерность в идеала I кольце многочленов R равна размерности Крулля кольца R / I равна размерности алгебраического множества нулей I. и Оно также равно числу гиперплоскостей общего положения , которые необходимы для пересечения с алгебраическим множеством, состоящим из конечного числа точек. Степень . идеала и связанного с ним алгебраического множества — это количество точек этого конечного пересечения, подсчитанное с кратностью В частности, степень гиперповерхности равна степени ее полинома определения.

И степень, и размерность зависят только от набора ведущих мономов базиса Грёбнера идеала при любом мономиальном порядке.

Размерность — это максимальный размер подмножества S переменных такого, что не существует старшего монома, зависящего только от переменных из S . Таким образом, если идеал имеет размерность 0, то для каждой переменной x существует старший моном в базисе Грёбнера, являющийся степенью x .

И размерность, и степень могут быть выведены из ряда Гильберта идеала, который представляет собой ряд ${\textstyle \sum _{i=0}^{\infty }d_{i}t^{i}}$, где $d_{i}$ — количество мономов степени i , не кратных ни одному из старших мономов базиса Грёбнера. Ряд Гильберта можно сложить в рациональную дробь.

$\sum _{i=0}^{\infty }d_{i}t^{i}={\frac {P(t)}{(1-t)^{d}}},$

где d - размерность идеала, а $P(t)$ является полиномом таким, что $P(1)$ есть степень идеала.

Хотя размерность и степень не зависят от выбора мономиального порядка, ряд Гильберта и многочлен $P(t)$ изменяются при изменении мономиального порядка.

Большинство систем компьютерной алгебры , которые предоставляют функции для вычисления базисов Грёбнера, также предоставляют функции для вычисления ряда Гильберта, а, следовательно, и размерности и степени.

Ликвидация

Вычисление базисов Грёбнера для мономиального порядка исключения позволяет использовать вычислительную теорию исключения . Это основано на следующей теореме.

Рассмотрим кольцо полиномов $K[x_{1},\ldots ,x_{n},y_{1},\ldots ,y_{m}]=K[X,Y],$ в котором переменные разделены на два подмножества X и Y . Давайте также выберем мономиальный порядок исключения, «исключающий» X , то есть мономиальный порядок, при котором два монома сравниваются путем сравнения сначала X -частей, а, только в случае равенства, рассмотрения Y -частей. Это означает, что моном, содержащий X -переменную, больше, чем любой моном, не зависящий от X .Если G — базис Грёбнера идеала I для этого мономиального порядка, то $G\cap K[Y]$ является базисом Грёбнера $I\cap K[Y]$ (этот идеал часто называют идеалом исключения ). Более того, $G\cap K[Y]$ состоит в точности из полиномов G, главные члены которых принадлежат K [ Y ] (это очень упрощает вычисление $G\cap K[Y]$, так как проверять нужно только ведущие мономы).

Это свойство исключения имеет множество применений, некоторые из которых описаны в следующих разделах.

Другое применение в алгебраической геометрии заключается в том, что исключение реализует геометрическую операцию проекции аффинного алгебраического множества в подпространство объемлющего пространства: с учетом приведенных выше обозначений ( замыкание Зарисского ) проекция алгебраического множества, определенного идеалом I в Y -подпространство определяется идеалом $I\cap K[Y].$

Лексикографический порядок такой, что $x_{1}>\cdots >x_{n}$ это порядок исключения для каждого раздела $\{x_{1},\ldots ,x_{k}\},\{x_{k+1},\ldots ,x_{n}\}.$ Таким образом, основа Грёбнера для этого упорядочения несет гораздо больше информации, чем обычно необходимо. Это может объяснить, почему базы Грёбнера для лексикографического упорядочения обычно труднее всего вычислить.

идеалы

Если I и J — два идеала, порожденные соответственно { f ₁ , ..., f _m } и { g ₁ , ..., g _k }, то одно вычисление базиса Грёбнера дает базис Грёбнера их пересечения I ∩ J . Для этого вводится новая неопределенная t и используется порядок исключения, так что первый блок содержит только t , а другой блок содержит все остальные переменные (это означает, что моном, содержащий t, больше, чем любой моном, который не содержит т ). При таком мономиальном порядке базис Грёбнера I ∩ J состоит из полиномов, не содержащих t , в базисе Грёбнера идеала

$K=\langle tf_{1},\ldots ,tf_{m},(1-t)g_{1},\ldots ,(1-t)g_{k}\rangle .$

Другими словами, I ∩ J получается удалением t из K .Это можно доказать, заметив, что идеал K состоит из многочленов $(a-b)t+b$ такой, что $a\in I$ и $b\in J$. Такой многочлен не зависит от t тогда и только тогда, когда a = b , что означает, что $b\in I\cap J.$

Имплицитизация рациональной кривой

— Рациональная кривая это алгебраическая кривая , имеющая систему параметрических уравнений вида

${\begin{aligned}x_{1}&={\frac {f_{1}(t)}{g_{1}(t)}}\\&\;\;\vdots \\x_{n}&={\frac {f_{n}(t)}{g_{n}(t)}},\end{aligned}}$

где $f_{i}(t)$ и $g_{i}(t)$ являются одномерными полиномами для 1 ≤ i ≤ n . Можно (и будет) предполагать, что $f_{i}(t)$ и $g_{i}(t)$ взаимно просты (у них нет непостоянных общих факторов).

Имплицитизация заключается в вычислении неявных уравнений такой кривой. В случае n = 2, то есть для плоских кривых, это можно вычислить с помощью результата . Неявное уравнение представляет собой следующий результат:

${\text{Res}}_{t}(g_{1}x_{1}-f_{1},g_{2}x_{2}-f_{2}).$

Исключение с помощью базисов Грёбнера позволяет неявно использовать любое значение n , просто исключив t в идеале. $\langle g_{1}x_{1}-f_{1},\ldots ,g_{n}x_{n}-f_{n}\rangle .$Если n = 2, то результат тот же, что и с результирующим, если отображение $t\mapsto (x_{1},x_{2})$ инъективен почти для любого t . В другом случае равнодействующая является степенью результата исключения.

Насыщенность

При моделировании задачи полиномиальными уравнениями часто предполагается, что некоторые величины отличны от нуля, чтобы избежать вырожденных случаев. Например, при работе с треугольниками многие свойства становятся ложными, если треугольник вырождается в отрезок прямой, т. е. длина одной стороны равна сумме длин других сторон. В таких ситуациях невозможно вывести соответствующую информацию из полиномиальной системы, если не игнорировать вырожденные решения. Точнее, система уравнений определяет алгебраическое множество , которое может иметь несколько неприводимых компонент , причем необходимо удалить те компоненты, на которых условия вырождения всюду равны нулю.

Это достигается путем насыщения уравнений условиями вырождения, что можно сделать с помощью свойства исключения базисов Грёбнера.

Определение насыщенности

Локализация кольца состоит в присоединении к нему формальных обратных некоторых элементов. В этом разделе рассматривается только случай одного элемента или, что то же самое, конечного числа элементов (присоединение обратных значений нескольких элементов эквивалентно присоединению обратного их произведения). Локализация — это кольца R элементом f кольцо $R_{f}=R[t]/(1-ft),$ где t — новая неопределенная величина, представляющая обратную величину f . Локализация — идеала I из R это идеал $R_{f}I$ из $I_{f}.$ Когда R — кольцо многочленов, вычисления в $R_{f}$ неэффективен из-за необходимости управлять знаменателями. Поэтому локализацию обычно заменяют операцией насыщения .

The насыщенность по f идеала I в R является прообразом $R_{f}I$ при каноническом отображении из R в $R_{f}.$ Это идеал $I:f^{\infty }=\{g\in R\mid (\exists k\in \mathbb {N} )f^{k}g\in I\}$ состоящий из всех элементов R, произведение которых с некоторой степенью f принадлежит I .

Если J — идеал, порожденный I и 1− ft в R [ t ], то $I:f^{\infty }=J\cap R.$ Отсюда следует, что, если R - кольцо многочленов, вычисление базиса Грёбнера, исключающее t , дает базис Грёбнера насыщения идеала многочленом.

, обеспечивающим удаление из алгебраического множества, определяемого идеалом I, неприводимых компонент , на которых многочлен f равен нулю, является следующее: первичное разложение Важным свойством насыщения $I:f^{\infty }$ состоит из компонент первичного разложения I, не содержащих степени f .

Расчет насыщенности

Базис Грёбнера насыщения f полиномиального идеала, порожденного конечным набором многочленов F , может быть получен путем исключения t в $F\cup \{1-tf\},$ то есть сохраняя полиномы независимыми от t в базисе Грёбнера $F\cup \{1-tf\}$ для порядка исключения, исключающего t .

Вместо использования F можно также начать с базиса F. Грёбнера Какой метод наиболее эффективен, зависит от проблемы. Однако, если насыщение не удаляет какой-либо компонент, то есть если идеал равен своему насыщенному идеалу, сначала вычисление базиса Грёбнера F обычно происходит быстрее. С другой стороны, если при насыщении удаляются некоторые компоненты, прямое вычисление может оказаться значительно быстрее.

Если кто-то хочет насытить по нескольким полиномам $f_{1},\ldots ,f_{k}$ или относительно одного многочлена, который является произведением $f=f_{1}\cdots f_{k},$ Есть три способа, которые дают один и тот же результат, но могут иметь очень разное время вычислений (это зависит от проблемы, которая является наиболее эффективной).

• Насыщение $f=f_{1}\cdots f_{k}$ за одно вычисление в базисе Грёбнера.
• Насыщение $f_{1},$ затем насыщаем результат $f_{2},$ и так далее.
• Добавляя к F или к его базису Грёбнера полиномы $1-t_{1}f_{1},\ldots ,1-t_{k}f_{k},$ и устранение $t_{i}$ за одно вычисление в базисе Грёбнера.

нулевой точке

Nullstellensatz Гильберта имеет две версии. Первый утверждает, что набор многочленов не имеет общих нулей над алгебраическим замыканием поля коэффициентов тогда и только тогда, когда 1 принадлежит порожденному идеалу. Это легко проверить с помощью вычисления базиса Грёбнера, потому что 1 принадлежит идеалу тогда и только тогда, когда 1 принадлежит базису Грёбнера идеала для любого мономиального порядка.

Вторая версия утверждает, что множество общих нулей (в алгебраическом замыкании поля коэффициентов) идеала содержится в гиперповерхности нулей многочлена f тогда и только тогда, когда степень f принадлежит идеалу . Это можно проверить, насытив идеал f ; на самом деле, степень f принадлежит идеалу тогда и только тогда, когда насыщение f обеспечивает базис Грёбнера, содержащий 1.

Имплицитация в высшем измерении

По определению аффинное рациональное многообразие размерности k можно описать параметрическими уравнениями вида

${\begin{aligned}x_{1}&={\frac {p_{1}}{p_{0}}}\\&\;\;\vdots \\x_{n}&={\frac {p_{n}}{p_{0}}},\end{aligned}}$

где $p_{0},\ldots ,p_{n}$ являются n +1 полиномами от k переменных (параметров параметризации) $t_{1},\ldots ,t_{k}.$ Таким образом, параметры $t_{1},\ldots ,t_{k}$ и координаты $x_{1},\ldots ,x_{n}$ точек многообразия являются нулями идеала

$I=\left\langle p_{0}x_{1}-p_{1},\ldots ,p_{0}x_{n}-p_{n}\right\rangle .$

Можно предположить, что достаточно исключить параметры, чтобы получить неявные уравнения многообразия, как это было сделано в случае кривых. К сожалению, это не всегда так. Если $p_{i}$ имеют общий нуль (иногда называемый базовой точкой ), каждый неприводимый компонент непустого алгебраического множества, определяемый $p_{i}$ является неприводимой компонентой алгебраического множества, определенного I . Отсюда следует, что в этом случае прямое устранение $t_{i}$ предоставляет пустой набор полиномов.

Следовательно, если k > 1, необходимы два базисных вычисления Грёбнера, чтобы импликировать:

1. Насыщать $I$ к $p_{0}$ чтобы получить базис Грёбнера $G$
2. Устранить $t_{i}$ от $G$ получить базис Грёбнера идеала (неявных уравнений) многообразия.

Алгоритмы и реализации

Алгоритм Бухбергера — старейший алгоритм вычисления базисов Грёбнера. Она была разработана Бруно Бухбергером вместе с базисной теорией Грёбнера. Его несложно реализовать, но вскоре выяснилось, что необработанные реализации могут решить только тривиальные проблемы. Основными проблемами являются следующие:

1. Даже если результирующий базис Грёбнера мал, промежуточные полиномы могут быть огромными. В результате большая часть вычислительного времени может быть потрачена на управление памятью . Таким образом, специализированные алгоритмы управления памятью могут стать фундаментальной частью эффективной реализации.
2. Целые числа, возникающие во время вычислений, могут быть достаточно большими, чтобы использовать быстрые алгоритмы умножения и многомодулярную арифметику . По этой причине большинство оптимизированных реализаций используют GMPlibrary . Кроме того, модульная арифметика , китайская теорема об остатках и лифтинг Гензеля. в оптимизированных реализациях используются
3. Выбор S-полиномов для приведения и полиномов, используемых для их приведения, посвящен эвристике . Как и во многих вычислительных задачах, эвристика не может обнаружить большинство скрытых упрощений, и если избегать эвристического выбора, можно добиться значительного повышения эффективности алгоритма.
4. В большинстве случаев большинство вычисляемых S-полиномов сводятся к нулю; то есть большая часть вычислительного времени тратится на вычисление нуля.
5. Мономиальный порядок , который чаще всего необходим для приложений (чисто лексикографический), не является тем порядком, который приводит к самым простым вычислениям, обычно это порядок degrevlex .

множество улучшений, вариантов и эвристик было предложено Для решения 3. до введения алгоритмов F4 и F5 Жаном -Шарлем Фожером . Поскольку эти алгоритмы разработаны для целых коэффициентов или с коэффициентами в целых числах по модулю простого числа , алгоритм Бухбергера остается полезным для более общих коэффициентов.

Грубо говоря, алгоритм F4 решает 3. путем замены множества S-полиномиальных сокращений на сокращение строк одной большой матрицы, для чего передовые методы линейной алгебры можно использовать . Это частично решает проблему 4., так как приведения к нулю в алгоритме Бухбергера соответствуют отношениям между строками сокращаемой матрицы, а нулевые строки приведенной матрицы соответствуют базису векторного пространства этих отношений.

Алгоритм F5 улучшает F4, вводя критерий, позволяющий уменьшить размер сокращаемых матриц. Этот критерий почти оптимален, поскольку приводимые матрицы имеют полный ранг в достаточно регулярных случаях (в частности, когда входные полиномы образуют регулярную последовательность ). Настройка F5 для общего использования сложна, поскольку его характеристики зависят от порядка входных полиномов и баланса между приращением степени рабочего полинома и количеством рассматриваемых входных полиномов. На сегодняшний день (2022 г.) не существует распределенной реализации, которая была бы значительно более эффективной, чем F4, но над модульными целыми числами F5 успешно использовался для решения нескольких криптографических задач ; например, за нарушение задачи HFE .

Проблема 5. была решена открытием алгоритмов преобразования базиса, которые начинаются с базиса Грёбнера для одного мономиального порядка для вычисления базиса Грёбнера для другого мономиального порядка. Алгоритм FGLM — это такой алгоритм преобразования базиса, который работает только в нульмерном случае (когда многочлены имеют конечное число комплексных общих нулей) и имеет полиномиальную сложность по числу общих нулей. Алгоритм преобразования базиса, который работает в общем случае, — это алгоритм обхода Грёбнера . В своей исходной форме FGLM может быть решающим шагом для решения систем полиномиальных уравнений , поскольку FGML не учитывает разреженность задействованных матриц . Это было исправлено введением разреженных алгоритмов FGLM .

общего назначения Большинство систем компьютерной алгебры имеют реализации одного или нескольких алгоритмов для базисов Грёбнера, часто также встроенных в другие функции, например, для решения систем полиномиальных уравнений или для упрощения тригонометрических функций; так обстоит дело, например, с CoCoA , GAP , Macaulay 2 , Magma , Maple , Mathematica , SINGULAR , SageMath и SymPy . Когда доступна F4, она обычно намного эффективнее алгоритма Бухбергера. Методы реализации и варианты алгоритмов не всегда документируются, хотя они могут существенно повлиять на эффективность.

Реализации F4 и (sparse)-FGLM включены в библиотеку Msolve . Помимо алгоритмов Грёбнера, Msolve содержит быстрые алгоритмы изоляции вещественных корней и объединяет все эти функции в алгоритм вещественных решений систем полиномиальных уравнений , который значительно превосходит другие программы для этой задачи (Maple и Magma). Msolve доступен на GitHub и взаимодействует с Julia , Maple и SageMath; это означает, что Msolve можно использовать непосредственно из этих программных сред.

Сложность

Сложность вычислений в базисе Грёбнера обычно оценивается с точки зрения количества n переменных и максимальной степени d входных полиномов.

В худшем случае основным параметром сложности является максимальная степень элементов результирующего приведенного базиса Грёбнера. Точнее, если базис Грёбнера содержит элемент большой степени D , то этот элемент может содержать $\Omega (D^{n})$ ненулевые члены, вычисление которых требует времени $\Omega (D^{n})>D^{\Omega (n)}.$ С другой стороны, если все многочлены в приведенном базисе Грёбнера ( однородный идеал) имеют степень не более D , базис Грёбнера может быть вычислен с помощью линейной алгебры в векторном пространстве многочленов степени меньше 2 D , которое имеет размерность $O(D^{n}).$ Итак, сложность этого вычисления $O(D^{n})^{O(1)}=D^{O(n)}.$

Наихудшая сложность вычисления базиса Грёбнера является дважды экспоненциальной по n . Точнее, сложность ограничена сверху полиномом от ${\textstyle d^{2^{n}}.}$ Поэтому, используя небольшое обозначение o , он ограничен ${\textstyle d^{2^{n+o(n)}}.}$ С другой стороны, были приведены примеры приведенных базисов Грёбнера, содержащих многочлены степени ${\textstyle d^{2^{\Omega (n)}},}$или содержащий ${\textstyle d^{2^{\Omega (n)}}}$ элементы. Поскольку каждый алгоритм вычисления базиса Грёбнера должен записывать свой результат, это обеспечивает нижнюю оценку сложности.

Базис Грёбнера EXPSPACE-полный .

Обобщения

Концепция и алгоритмы базисов Грёбнера обобщены на подмодули над свободных модулей кольцом полиномов. В самом деле, если L — свободный модуль над кольцом R , то можно рассмотреть прямую сумму $R\oplus L$ как кольцо, определив произведение двух элементов L равным 0 . Это кольцо можно отождествить с $R[e_{1},\ldots ,e_{l}]/\left\langle \{e_{i}e_{j}|1\leq i\leq j\leq l\}\right\rangle$, где $e_{1},\ldots ,e_{l}$ основой Л. является Это позволяет идентифицировать подмодуль L, порожденный $g_{1},\ldots ,g_{k}$ с идеалом $R[e_{1},\ldots ,e_{l}]$ созданный $g_{1},\ldots ,g_{k}$ и продукты $e_{i}e_{j}$, $1\leq i\leq j\leq l$. Если R — кольцо полиномов, то это сводит теорию и алгоритмы базисов Грёбнера модулей к теории и алгоритмам базисов Грёбнера идеалов.

Концепция и алгоритмы базисов Грёбнера также были обобщены на идеалы над различными кольцами, коммутативными или нет, такими как кольца полиномов над кольцом главных идеалов или алгебры Вейля .

Области применения

Коды, исправляющие ошибки

Базис Грёбнера был применен в теории кодов, исправляющих ошибки, для алгебраического декодирования. Используя базисные вычисления Грёбнера для различных форм уравнений, исправляющих ошибки, были разработаны методы декодирования для исправления ошибок циклических кодов. аффинные коды разновидностей, алгебро-геометрические коды и даже общие линейные блочные коды. Применение базиса Грёбнера в алгебраическом декодировании до сих пор остается областью исследований теории канального кодирования.

См. также

• Лемма Бергмана о ромбе , расширение базисов Грёбнера на некоммутативные кольца.
• Основа Грейвера
• Джанет базис
• Регулярные цепочки , альтернативный способ представления алгебраических множеств

Дальнейшее чтение

• Адамс, Уильям В.; Лустаунау, Филипп (1994). Введение в базисы Грёбнера . Аспирантура по математике . Том. 3. Американское математическое общество . ISBN  0-8218-3804-0 .
• Ли, Хуэйши (2011). Базисы Грёбнера в теории колец . Всемирная научная . ISBN  978-981-4365-13-0 .
• Беккер, Томас; Вайспфеннинг, Волкер (1998). Базисы Грёбнера: вычислительный подход к коммутативной алгебре . Тексты для аспирантов по математике. Том. 141. Спрингер. ISBN  0-387-97971-9 .
• Бухбергер, Бруно (1965). Алгоритм поиска базисных элементов кольца классов вычетов нульмерного полиномиального идеала (PDF) (доктор философии). Университет Инсбрука. — (2006). «Докторская диссертация Бруно Бухбергера, 1965 год: Алгоритм поиска базисных элементов кольца классов вычетов нульмерного полиномиального идеала» . Журнал символических вычислений . 41 (3–4). Перевод Абрамсона М.: 471–511. дои : 10.1016/j.jsc.2005.09.007 . [Это диссертация Бухбергера, посвященная созданию базисов Грёбнера.]
• Бухбергер, Бруно (1970). «Алгоритмический критерий разрешимости системы алгебраических уравнений» (PDF) . Математические уравнения . 4 : 374–383. дои : 10.1007/BF01844169 . S2CID   189834323 . (Это журнальная публикация диссертации Бухбергера.) Бурчбергер, Б.; Винклер Ф., ред. (26 февраля 1998 г.). «Алгоритмический критерий разрешимости системы алгебраических уравнений» . Базисы и приложения Грёбнера . Серия лекций Лондонского математического общества. Том. 251. Издательство Кембриджского университета. стр. 535–545. ISBN  978-0-521-63298-0 .
• Бухбергер, Бруно; Кауэрс, Мануэль (2010). «Базы Грёбнера» . Схоларпедия . 5 (10): 7763. Бибкод : 2010SchpJ...5.7763B . doi : 10.4249/scholarpedia.7763 .
• Фрёберг, Ральф (1997). Введение в базисы Грёбнера . Уайли. ISBN  0-471-97442-0 .
• Штурмфельс, Бернд (ноябрь 2005 г.). «Что такое… базис Грёбнера?» (PDF) . Уведомления Американского математического общества . 52 (10): 1199–1200, краткое введение. {{cite journal}}: CS1 maint: постскриптум ( ссылка )
• Ширшов, Анатолий И. (1999). «Некоторые алгоритмические проблемы для алгебр Ли» (PDF) . Бюллетень ACM SIGSAM . 33 (2): 3–6. дои : 10.1145/334714.334715 . S2CID   37070503 . (перевод из Сиб. Матем. Ж. Сибирский математический журнал 3 (1962), 292–296).
• Ашенбреннер, Матиас ; Хиллар, Кристофер (2007). «Конечное порождение симметричных идеалов» . Труды Американского математического общества . 359 (11): 5171–92. arXiv : math/0411514 . дои : 10.1090/S0002-9947-07-04116-5 . S2CID   5656701 . (о бесконечномерных базисах Грёбнера для колец многочленов от бесконечного числа неопределённых).

Внешние ссылки

• Собственная реализация Фожером его алгоритма F4.
• «Базис Грёбнера» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Бухбергер, Б. (2003). «Базы Грёбнера: краткое введение для системных теоретиков» (PDF) . В Морено-Диас, Р.; Бухбергер, Б.; Фрейре, Дж. (ред.). Теория компьютерных систем — EUROCAST 2001: Подборка статей с 8-го международного семинара по теории компьютерных систем . Спрингер. стр. 1–19. ISBN  978-3-540-45654-4 .
• Бухбергер, Б.; Заплетал, А. «Библиография по основам Грёбнера» .
• Страница сравнения таймингов для программного обеспечения Gröbner Bases
• Профессор Бруно Бухбергер Бруно Бухбергер
• Вайсштейн, Эрик В. «Базис Грёбнера» . Математический мир .
• Введение в основу Грёбнера в Scholarpedia