Дициклическая группа

В теории групп — дициклическая группа (обозначение Dic _n или Q _{4 n} , ⟨ п , 2,2⟩ ) — особый вид неабелевой группы порядка 4 > 1 n ( n ). Это расширение циклической группы порядка 2 циклической группой порядка 2 n , что дало название дициклической . В обозначениях точных последовательностей групп это расширение можно выразить как:

$1\to C_{2n}\to {\mbox{Dic}}_{n}\to C_{2}\to 1.\,$

В более общем смысле, учитывая любую конечную абелеву группу с элементом порядка 2, можно определить дициклическую группу.

Определение

Для каждого целого числа n > 1 дициклическая группа Dic _n может быть определена как подгруппа единичных кватернионов, порожденных

${\begin{aligned}a&=e^{\frac {i\pi }{n}}=\cos {\frac {\pi }{n}}+i\sin {\frac {\pi }{n}}\\x&=j\end{aligned}}$

Более абстрактно, можно определить дициклическую группу Dic _n как группу со следующим представлением

$\operatorname {Dic} _{n}=\left\langle a,x\mid a^{2n}=1,\ x^{2}=a^{n},\ x^{-1}ax=a^{-1}\right\rangle .\,\!$

Некоторые вещи, которые следует отметить из этого определения:

• $x^{4}=1$
• $x^{2}a^{m}=a^{m+n}=a^{m}x^{2}$
• если $l=\pm 1$, затем $x^{l}a^{m}=a^{-m}x^{l}$
• $a^{m}x^{-1}=a^{m-n}a^{n}x^{-1}=a^{m-n}x^{2}x^{-1}=a^{m-n}x$

Таким образом, каждый элемент Dic _n можно однозначно записать в виде ^м х ^л , где 0 ≤ m < 2 n и l = 0 или 1. Правила умножения имеют вид

• $a^{k}a^{m}=a^{k+m}$
• $a^{k}a^{m}x=a^{k+m}x$
• $a^{k}xa^{m}=a^{k-m}x$
• $a^{k}xa^{m}x=a^{k-m+n}$

Отсюда следует, что Dic _n имеет порядок 4 n .

Когда n дициклическая группа изоморфна группе кватернионов Q. = 2 , В более общем смысле, когда n является степенью двойки, дициклическая группа изоморфна обобщенной группе кватернионов .

Характеристики

Для каждого n > 1 дициклическая группа Dic _n является неабелевой группой порядка 4 n . (Для вырожденного случая n = 1 группа Dic ₁ является циклической группой C ₄ , которая не считается дициклической.)

Пусть A = ⟨ a ⟩ — подгруппа Dic _n порожденная a , . Тогда A — циклическая группа порядка 2 n , поэтому [Dic _n : A ] = 2. Как подгруппа индекса 2 она автоматически является нормальной подгруппой . Факторгруппа Dic _n / A является циклической группой порядка 2.

Dic _n разрешима ​ ; обратите внимание, что A является нормальным и, будучи абелевым, само разрешимо.

Бинарная группа диэдра

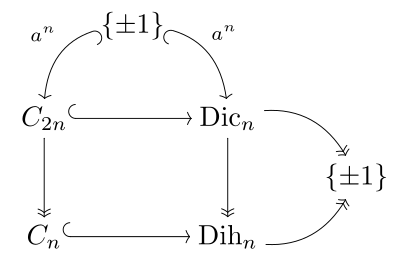
Дициклическая группа представляет собой бинарную группу многогранников — это один из классов подгрупп группы Pin Pin _— (2), которая является подгруппой группы Spin Spin (3) — и в этом контексте известна как бинарный диэдр. группа .

Связь с бинарной циклической группой C _{2 n} , циклической группой C _n и группой диэдра Dih _n порядка 2 n показана на диаграмме справа и параллельна соответствующей диаграмме для группы Pin. Коксетер записывает бинарную группу диэдра как ⟨2,2, n ⟩ и бинарную циклическую группу с угловыми скобками, ⟨ n ⟩.

Существует внешнее сходство между дициклическими группами и диэдральными группами ; оба являются своего рода «зеркалированием» базовой циклической группы. Но представление группы диэдра будет иметь x ² = 1 вместо x ² = а ^н ; и это дает другую структуру. В частности, Dic _n не является полупрямым произведением A и ⟨ x ⟩ , поскольку A ∩ ⟨ x ⟩ не тривиально.

Дициклическая группа имеет единственную инволюцию (т.е. элемент порядка 2), а именно x ² = а ^н . Обратите внимание, что этот элемент лежит в центре Dic _n . Действительно, центр состоит исключительно из единичного элемента и x ² . Если мы добавим отношение x ² = 1 к представлению Dic _n, получается представление группы диэдра Dih _n , поэтому факторгруппа Dic _n /< x ² > изоморфен Dih _n .

Существует естественный гомоморфизм 2-к-1 группы единичных кватернионов в трехмерную группу вращений, описанную в кватернионах и пространственных вращениях . Поскольку дициклическая группа может быть вложена внутрь единичных кватернионов, можно задаться вопросом, каков ее образ при этом гомоморфизме. Ответ – это просто группа диэдральной симметрии Dih _n . По этой причине дициклическая группа также известна как группа бинарного диэдра . Заметим, что дициклическая группа не содержит подгрупп, изоморфных Dih _n .

Аналогичная конструкция прообраза с использованием Pin ₊ (2) вместо Pin ₋ (2) дает другую группу диэдра Dih _{2 n} , а не дициклическую группу.

Обобщения

Пусть A — абелева группа , имеющая определенный элемент y в A порядка 2. Группа G называется обобщенной дициклической группой , записываемой как Dic( A , y ) , если она порождается A и дополнительным элементом x , и кроме того, мы имеем, что [ G : A ] = 2, x ² = y , и для всех a в A , x ⁻¹ топор = а ⁻¹ .

Поскольку для циклической группы четного порядка всегда существует единственный элемент порядка 2, мы видим, что дициклические группы — это всего лишь особый тип обобщенной дициклической группы.

Дициклическая группа – это случай $(p,q,r)=(2,2,n)$ семейства бинарных групп треугольников $\Gamma (p,q,r)$ определяется презентацией: [1]

$\langle a,b,c\mid a^{p}=b^{q}=c^{r}=abc\rangle .$

Факторизируя по дополнительному соотношению $abc=e$ образует обычную группу треугольников , которая в данном случае является двугранным фактором $\mathrm {Dic} _{n}\rightarrow \mathrm {Dih} _{n}$.

См. также

• бинарная многогранная группа
• бинарная циклическая группа , ⟨ n ⟩, порядок 2 n
• бинарная тетраэдрическая группа , 2T = ⟨2,3,3⟩, заказать 24
• бинарная октаэдрическая группа , 2O = ⟨2,3,4⟩, заказать 48
• бинарная группа икосаэдра , 2I = ⟨2,3,5⟩, заказать 120

Ссылки

• Коксетер, HSM (1974), «7.1 Циклические и дициклические группы», Правильные комплексные многогранники , Cambridge University Press, стр. 74–75 .
• Коксетер, HSM; Мозер, WOJ (1980). Генераторы и соотношения для дискретных групп . Нью-Йорк: Springer-Verlag. ISBN  0-387-09212-9 .

Внешние ссылки

• Дициклические группы в GroupNames