Группа кватернионов

Таблица умножения группы кватернионов (упрощенная форма)

	1	я	дж	к
1	1	я	дж	к
я	я	−1	к	− j
дж	дж	- к	−1	я
к	к	дж	- я	−1

Циклическая диаграмма Q ₈ . Каждый цвет определяет серию степеней любого элемента, связанного с единичным элементом e = 1. Например, красный цикл отражает тот факт, что i ² = е , я ³ = я и я ⁴ = е. Красный цикл также отражает то, что я ² = е , я ³ = я и я ⁴ = е.

В теории групп группа кватернионов Q ₈ (иногда обозначаемая просто Q) — неабелева группа , восьмого порядка изоморфная восьмиэлементному подмножеству $\{1,i,j,k,-1,-i,-j,-k\}$ кватернионов при умножении . Это дается групповой презентацией.

$\mathrm {Q} _{8}=\langle {\bar {e}},i,j,k\mid {\bar {e}}^{2}=e,\;i^{2}=j^{2}=k^{2}=ijk={\bar {e}}\rangle ,$

где e — единичный элемент, а e коммутирует с другими элементами группы. Эти отношения, открытые У. Р. Гамильтоном , также порождают кватернионы как алгебру над действительными числами.

Еще одна презентация вопроса ₈ :

$\mathrm {Q} _{8}=\langle a,b\mid a^{4}=e,a^{2}=b^{2},ba=a^{-1}b\rangle .$

Как и многие другие конечные группы, ее можно реализовать как группу Галуа некоторого поля алгебраических чисел .

По сравнению с группой диэдра

Группа кватернионов Q ₈ имеет тот же порядок, что и группа диэдра D ₄ , но другую структуру, как показывают их графы Кэли и циклов:

	QQ8	Д 4
Граф Кэли	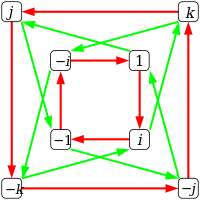Красные стрелки соединяют g → gi , зеленые соединяют g → gj .
График цикла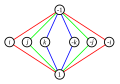

На диаграммах для D ₄ элементы группы отмечены их действием на букву F в определяющем представлении R. ² . То же самое нельзя сделать для Q ₈ , поскольку он не имеет точного представления в R ² или Р ³ . D ₄ может быть реализован как подмножество разделенных кватернионов таким же образом, как Q ₈ можно рассматривать как подмножество кватернионов.

Таблица Кэли

Таблица Кэли (таблица умножения) для Q ₈ имеет вид:

×	и	и	я	я	дж	дж	к	к
и	и	и	я	я	дж	дж	к	к
и	и	и	я	я	дж	дж	к	к
я	я	я	и	и	к	к	дж	дж
я	я	я	и	и	к	к	дж	дж
дж	дж	дж	к	к	и	и	я	я
дж	дж	дж	к	к	и	и	я	я
к	к	к	дж	дж	я	я	и	и
к	к	к	дж	дж	я	я	и	и

Свойства

Все элементы i , j и k имеют четвертый порядок в Q ₈ , и любые два из них порождают всю группу. Еще одна презентация Q ₈ основанный только на двух элементах для пропуска этой избыточности:

$\left\langle x,y\mid x^{4}=1,x^{2}=y^{2},y^{-1}xy=x^{-1}\right\rangle .$

Например, записывая элементы группы в лексикографически минимальных нормальных формах, можно идентифицировать:

$\{e,{\bar {e}},i,{\bar {i}},j,{\bar {j}},k,{\bar {k}}\}\leftrightarrow \{e,x^{2},x,x^{3},y,x^{2}y,xy,x^{3}y\}.$

Группа кватернионов обладает необычным свойством быть гамильтоновой : Q ₈ неабелева, но подгруппа нормальна каждая . Каждая гамильтонова группа содержит копию Q ₈ .

Группа кватернионов Q ₈ и группа диэдра D ₄ являются двумя наименьшими примерами нильпотентной неабелевой группы.

Центром является и коммутантом группы Q ₈ подгруппа $\{e,{\bar {e}}\}$. Внутренняя группа автоморфизмов Q ₈ задается группой по модулю ее центра, т. е. фактор-группой $\mathrm {Q} _{8}/\{e,{\bar {e}}\},$ которая изоморфна четырехгруппе Клейна V. Полная группа автоморфизмов Q ₈ изоморфна , S ₄ , симметричной группе из четырех букв (см. Матричные представления ниже), а внешняя группа автоморфизмов Q ₈ таким образом, равна S ₄ / V, который изоморфен S ₃ .

Группа кватернионов Q ₈ имеет пять классов сопряженности: $\{e\},\{{\bar {e}}\},\{i,{\bar {i}}\},\{j,{\bar {j}}\},\{k,{\bar {k}}\},$ и, таким образом, пять неприводимых представлений над комплексными числами размерностей 1, 1, 1, 1, 2:

Тривиальное представление .

Представления знаков с i, j, k-ядром : Q ₈ имеет три максимальные нормальные подгруппы: циклические подгруппы, порожденные i, j и k соответственно. Для каждой максимальной нормальной подгруппы N мы получаем одномерное представление, факторизуемое через 2-элементную факторгруппу G / N . Представление отправляет элементы N в 1, а элементы за пределами N в -1.

2-мерное представление : описано ниже в разделе «Матричные представления» . Оно нереализуемо для действительных чисел , но представляет собой сложное представление: действительно, это всего лишь кватернионы. $\mathbb {H}$ рассматривается как алгебра над $\mathbb {C}$, а действие — умножение слева на $Q_{8}\subset \mathbb {H}$.

Таблица символов Q8 _у оказывается такой же, как и _D4 :

Представление(ρ)/Класс сопряженности	{ и }	{ и }	{ я, я }	{Дж, Дж }	{ к, к }
Тривиальное представление	1	1	1	1	1
Представление знака с помощью i-kernel	1	1	1	−1	−1
Представление знаков с помощью j-ядра	1	1	−1	1	−1
Представление знака с помощью k-ядра	1	1	−1	−1	1
2-мерное представление	2	−2	0	0	0

Тем не менее, все неприводимые характеры $\chi _{\rho }$ в строках выше имеют действительные значения, это дает разложение вещественной групповой алгебры $G=\mathrm {Q} _{8}$ на минимальные двусторонние идеалы :

$\mathbb {R} [\mathrm {Q} _{8}]=\bigoplus _{\rho }(e_{\rho }),$

где идемпотенты $e_{\rho }\in \mathbb {R} [\mathrm {Q} _{8}]$ соответствуют неприводимым:

$e_{\rho }={\frac {\dim(\rho )}{|G|}}\sum _{g\in G}\chi _{\rho }(g^{-1})g,$

так что

${\begin{aligned}e_{\text{triv}}&={\tfrac {1}{8}}(e+{\bar {e}}+i+{\bar {i}}+j+{\bar {j}}+k+{\bar {k}})\\e_{i{\text{-ker}}}&={\tfrac {1}{8}}(e+{\bar {e}}+i+{\bar {i}}-j-{\bar {j}}-k-{\bar {k}})\\e_{j{\text{-ker}}}&={\tfrac {1}{8}}(e+{\bar {e}}-i-{\bar {i}}+j+{\bar {j}}-k-{\bar {k}})\\e_{k{\text{-ker}}}&={\tfrac {1}{8}}(e+{\bar {e}}-i-{\bar {i}}-j-{\bar {j}}+k+{\bar {k}})\\e_{2}&={\tfrac {2}{8}}(2e-2{\bar {e}})={\tfrac {1}{2}}(e-{\bar {e}})\end{aligned}}$

Каждый из этих неприводимых идеалов изоморфен вещественной центральной простой алгебре , первые четыре — вещественному полю. $\mathbb {R}$. Последний идеал $(e_{2})$ изоморфно телу кватернионов ​ $\mathbb {H}$ по переписке:

${\begin{aligned}{\tfrac {1}{2}}(e-{\bar {e}})&\longleftrightarrow 1,\\{\tfrac {1}{2}}(i-{\bar {i}})&\longleftrightarrow i,\\{\tfrac {1}{2}}(j-{\bar {j}})&\longleftrightarrow j,\\{\tfrac {1}{2}}(k-{\bar {k}})&\longleftrightarrow k.\end{aligned}}$

Более того, гомоморфизм проекций $\mathbb {R} [\mathrm {Q} _{8}]\to (e_{2})\cong \mathbb {H}$ данный $r\mapsto re_{2}$ имеет идеал ядра, порожденный идемпотентом:

$e_{2}^{\perp }=e_{1}+e_{i{\text{-ker}}}+e_{j{\text{-ker}}}+e_{k{\text{-ker}}}={\tfrac {1}{2}}(e+{\bar {e}}),$

поэтому кватернионы также можно получить как факторкольцо $\mathbb {R} [\mathrm {Q} _{8}]/(e+{\bar {e}})\cong \mathbb {H}$. Обратите внимание, что это неприводимо как реальное представление $Q_{8}$, но распадается на две копии двумерной неприводимой при расширении до комплексных чисел. Действительно, комплексная групповая алгебра $\mathbb {C} [\mathrm {Q} _{8}]\cong \mathbb {C} ^{\oplus 4}\oplus M_{2}(\mathbb {C} ),$ где $M_{2}(\mathbb {C} )\cong \mathbb {H} \otimes _{\mathbb {R} }\mathbb {C} \cong \mathbb {H} \oplus \mathbb {H}$ — алгебра бикватернионов .

Матричные представления

Таблица умножения группы кватернионов как подгруппы SL (2, C ). Записи представлены секторами, соответствующими их аргументам: 1 (зеленый), i (синий), −1 (красный), − i (желтый).

Описанное выше двумерное неприводимое комплексное представление дает группу кватернионов Q ₈ как подгруппу общей линейной группы. $\operatorname {GL} (2,\mathbb {C} )$. Группа кватернионов — это мультипликативная подгруппа алгебры кватернионов:

$\mathbb {H} =\mathbb {R} 1+\mathbb {R} i+\mathbb {R} j+\mathbb {R} k=\mathbb {C} 1+\mathbb {C} j,$

который имеет регулярное представление $\rho :\mathbb {H} \to \operatorname {M} (2,\mathbb {C} )$ умножением слева на себя, рассматриваемого как комплексное векторное пространство с базисом $\{1,j\},$ так что $z\in \mathbb {H}$ соответствует $\mathbb {C}$-линейное картографирование $\rho _{z}:a+jb\mapsto z\cdot (a+jb).$ Полученное представление

${\begin{cases}\rho :\mathrm {Q} _{8}\to \operatorname {GL} (2,\mathbb {C} )\\g\longmapsto \rho _{g}\end{cases}}$

дается:

${\begin{matrix}e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}&i\mapsto {\begin{pmatrix}i&0\\0&\!\!\!\!-i\end{pmatrix}}&j\mapsto {\begin{pmatrix}0&\!\!\!\!-1\\1&0\end{pmatrix}}&k\mapsto {\begin{pmatrix}0&\!\!\!\!-i\\\!\!\!-i&0\end{pmatrix}}\\{\overline {e}}\mapsto {\begin{pmatrix}\!\!\!-1&0\\0&\!\!\!\!-1\end{pmatrix}}&{\overline {i}}\mapsto {\begin{pmatrix}\!\!\!-i&0\\0&i\end{pmatrix}}&{\overline {j}}\mapsto {\begin{pmatrix}0&1\\\!\!\!-1&0\end{pmatrix}}&{\overline {k}}\mapsto {\begin{pmatrix}0&i\\i&0\end{pmatrix}}.\end{matrix}}$

Поскольку все приведенные выше матрицы имеют единичный определитель, это представление Q ₈ в специальной линейной группе $\operatorname {SL} (2,\mathbb {C} )$.

Вариант дает представление унитарными матрицами (таблица справа). Позволять $g\in \mathrm {Q} _{8}$ соответствуют линейному отображению $\rho _{g}:a+bj\mapsto (a+bj)\cdot jg^{-1}j^{-1},$ так что $\rho :\mathrm {Q} _{8}\to \operatorname {SU} (2)$ дается:

${\begin{matrix}e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}&i\mapsto {\begin{pmatrix}i&0\\0&\!\!\!\!-i\end{pmatrix}}&j\mapsto {\begin{pmatrix}0&1\\\!\!\!-1&0\end{pmatrix}}&k\mapsto {\begin{pmatrix}0&i\\i&0\end{pmatrix}}\\{\overline {e}}\mapsto {\begin{pmatrix}\!\!\!-1&0\\0&\!\!\!\!-1\end{pmatrix}}&{\overline {i}}\mapsto {\begin{pmatrix}\!\!\!-i&0\\0&i\end{pmatrix}}&{\overline {j}}\mapsto {\begin{pmatrix}0&\!\!\!\!-1\\1&0\end{pmatrix}}&{\overline {k}}\mapsto {\begin{pmatrix}0&\!\!\!\!-i\\\!\!\!-i&0\end{pmatrix}}.\end{matrix}}$

Стоит отметить, что физики используют исключительно другое соглашение для $\operatorname {SU} (2)$ матричное представление для связи с обычными матрицами Паули :

${\begin{matrix}&e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}=\quad \,1_{2\times 2}&i\mapsto {\begin{pmatrix}0&\!\!\!-i\!\\\!\!-i\!\!&0\end{pmatrix}}=-i\sigma _{x}&j\mapsto {\begin{pmatrix}0&\!\!\!-1\!\\1&0\end{pmatrix}}=-i\sigma _{y}&k\mapsto {\begin{pmatrix}\!\!-i\!\!&0\\0&i\end{pmatrix}}=-i\sigma _{z}\\&{\overline {e}}\mapsto {\begin{pmatrix}\!\!-1\!&0\\0&\!\!\!-1\!\end{pmatrix}}=-1_{2\times 2}&{\overline {i}}\mapsto {\begin{pmatrix}0&i\\i&0\end{pmatrix}}=\,\,\,\,i\sigma _{x}&{\overline {j}}\mapsto {\begin{pmatrix}0&1\\\!\!-1\!\!&0\end{pmatrix}}=\,\,\,\,i\sigma _{y}&{\overline {k}}\mapsto {\begin{pmatrix}i&0\\0&\!\!\!-i\!\end{pmatrix}}=\,\,\,\,i\sigma _{z}.\end{matrix}}$

Этот конкретный выбор удобен и элегантен при описании состояний со спином 1/2 в $({\vec {J}}^{2},J_{z})$ базисе и учитывает операторы лестницы углового момента $J_{\pm }=J_{x}\pm iJ_{y}.$

Таблица умножения группы кватернионов как подгруппы SL(2,3) . Элементы поля обозначаются 0, +, −.

Существует также важное действие Q8 _на двумерное векторное пространство над конечным полем $\mathbb {F} _{3}=\{0,1,-1\}$ (таблица справа). Модульное представление $\rho :\mathrm {Q} _{8}\to \operatorname {SL} (2,3)$ дается

${\begin{matrix}e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}&i\mapsto {\begin{pmatrix}1&1\\1&\!\!\!\!-1\end{pmatrix}}&j\mapsto {\begin{pmatrix}\!\!\!-1&1\\1&1\end{pmatrix}}&k\mapsto {\begin{pmatrix}0&\!\!\!\!-1\\1&0\end{pmatrix}}\\{\overline {e}}\mapsto {\begin{pmatrix}\!\!\!-1&0\\0&\!\!\!\!-1\end{pmatrix}}&{\overline {i}}\mapsto {\begin{pmatrix}\!\!\!-1&\!\!\!\!-1\\\!\!\!-1&1\end{pmatrix}}&{\overline {j}}\mapsto {\begin{pmatrix}1&\!\!\!\!-1\\\!\!\!-1&\!\!\!\!-1\end{pmatrix}}&{\overline {k}}\mapsto {\begin{pmatrix}0&1\\\!\!\!-1&0\end{pmatrix}}.\end{matrix}}$

Это представление можно получить из поля расширения :

$\mathbb {F} _{9}=\mathbb {F} _{3}[k]=\mathbb {F} _{3}1+\mathbb {F} _{3}k,$

где $k^{2}=-1$ и мультипликативная группа $\mathbb {F} _{9}^{\times }$ имеет четыре генератора, $\pm (k\pm 1),$ порядка 8. Для каждого $z\in \mathbb {F} _{9},$ двумерный $\mathbb {F} _{3}$-векторное пространство $\mathbb {F} _{9}$ допускает линейное отображение:

${\begin{cases}\mu _{z}:\mathbb {F} _{9}\to \mathbb {F} _{9}\\\mu _{z}(a+bk)=z\cdot (a+bk)\end{cases}}$

Кроме того, мы имеем автоморфизм Фробениуса $\phi (a+bk)=(a+bk)^{3}$ удовлетворяющий $\phi ^{2}=\mu _{1}$ и $\phi \mu _{z}=\mu _{\phi (z)}\phi .$ Тогда приведенные выше матрицы представления будут следующими:

${\begin{aligned}\rho ({\bar {e}})&=\mu _{-1},\\\rho (i)&=\mu _{k+1}\phi ,\\\rho (j)&=\mu _{k-1}\phi ,\\\rho (k)&=\mu _{k}.\end{aligned}}$

Это представление реализует Q ₈ как нормальную подгруппу GL (2, 3) . Таким образом, для каждой матрицы $m\in \operatorname {GL} (2,3)$, мы имеем групповой автоморфизм

${\begin{cases}\psi _{m}:\mathrm {Q} _{8}\to \mathrm {Q} _{8}\\\psi _{m}(g)=mgm^{-1}\end{cases}}$

с $\psi _{I}=\psi _{-I}=\mathrm {id} _{\mathrm {Q} _{8}}.$ Фактически, они дают полную группу автоморфизмов как:

$\operatorname {Aut} (\mathrm {Q} _{8})\cong \operatorname {PGL} (2,3)=\operatorname {GL} (2,3)/\{\pm I\}\cong S_{4}.$

Она изоморфна симметрической группе S _4, поскольку линейные отображения $m:\mathbb {F} _{3}^{2}\to \mathbb {F} _{3}^{2}$ переставить четыре одномерных подпространства $\mathbb {F} _{3}^{2},$ т. е. четыре точки проективного пространства $\mathbb {P} ^{1}(\mathbb {F} _{3})=\operatorname {PG} (1,3).$

Кроме того, это представление переставляет местами восемь ненулевых векторов $\mathbb {F} _{3}^{2},$ дающее вложение Q ₈ в симметрическую группу S ₈ в дополнение к вложениям, заданным регулярными представлениями.

Группа Галуа

Ричард Дедекинд рассмотрел поле $\mathbb {Q} [{\sqrt {2}},{\sqrt {3}}]$ в попытке связать группу кватернионов с теорией Галуа . В 1936 году Эрнст Витт опубликовал свой подход к группе кватернионов на основе теории Галуа.

В 1981 году Ричард Дин показал, что группа кватернионов может быть реализована как группа Галуа Gal(T/ Q ), где Q — поле рациональных чисел , а T — поле расщепления многочлена.

$x^{8}-72x^{6}+180x^{4}-144x^{2}+36$.

В разработке используется фундаментальная теорема теории Галуа для определения четырех промежуточных полей между Q и T и их группами Галуа, а также две теоремы о циклическом расширении четвертой степени над полем.

группа

Обобщенная группа кватернионов Q _{4 n} порядка 4 n определяется представлением

$\langle x,y\mid x^{2n}=y^{4}=1,x^{n}=y^{2},y^{-1}xy=x^{-1}\rangle$

для целого числа n ≥ 2 с обычной группой кватернионов, заданной n = 2. Коксетер называет Q _{4 n} дициклической группой. $\langle 2,2,n\rangle$, частный случай бинарной группы многогранников $\langle \ell ,m,n\rangle$ и относится к группе многогранников $(p,q,r)$ и группа диэдра $(2,2,n)$. Обобщенная группа кватернионов может быть реализована как подгруппа $\operatorname {GL} _{2}(\mathbb {C} )$ созданный

$\left({\begin{array}{cc}\omega _{n}&0\\0&{\overline {\omega }}_{n}\end{array}}\right){\mbox{ and }}\left({\begin{array}{cc}0&-1\\1&0\end{array}}\right)$

где $\omega _{n}=e^{i\pi /n}$. Его также можно реализовать как подгруппу единичных кватернионов, порожденную $x=e^{i\pi /n}$ и $y=j$.

Обобщенные группы кватернионов обладают тем свойством, что каждая абелева подгруппа является циклической. Можно показать, что конечная p -группа с этим свойством (каждая абелева подгруппа циклическая) является либо циклической, либо обобщенной группой кватернионов, как определено выше. Другая характеристика состоит в том, что конечная p -группа, в которой существует единственная подгруппа порядка p, является либо циклической, либо 2-группой, изоморфной обобщенной группе кватернионов. В частности, для конечного поля F с нечетной характеристикой 2-силовская подгруппа в SL ₂ ( F ) неабелева и имеет только одну подгруппу порядка 2, поэтому эта 2-силовская подгруппа должна быть обобщенной группой кватернионов, ( Горенштейн 1980 , с. 42). Позволяя п ^р — размер F , где p — простое число, размер 2-силовской подгруппы SL ₂ ( F ) равен 2 ^н , где n = ord ₂ ( p ² - 1) + ord ₂ ( р ) .

Теорема Брауэра –Сузуки показывает, что группы, силовские 2-подгруппы которых являются обобщенными кватернионами, не могут быть простыми.

Другая терминология оставляет за собой название «обобщенная группа кватернионов» для дициклической группы порядка степени 2, который допускает представление

$\langle x,y\mid x^{2^{m}}=y^{4}=1,x^{2^{m-1}}=y^{2},y^{-1}xy=x^{-1}\rangle .$

См. также

• 16-ячеечный
• Бинарная тетраэдрическая группа
• Алгебра Клиффорда
• Дициклическая группа
• Целочисленный кватернион Гурвица
• Список малых групп

Ссылки

• Артин, Майкл (1991), Алгебра , Прентис Холл, ISBN  978-0-13-004763-2
• Браун, Кеннет С. (1982), Когомологии групп (3-е изд.), Springer-Verlag, ISBN  978-0-387-90688-1
• Картан, Анри ; Эйленберг, Сэмюэл (1999), Гомологическая алгебра , Princeton University Press, ISBN  978-0-691-04991-5
• Коксетер, HSM и Мозер, WOJ (1980). Генераторы и соотношения для дискретных групп . Нью-Йорк: Springer-Verlag. ISBN  0-387-09212-9 .
• Дин, Ричард А. (1981) «Рациональный полином, группой которого являются кватернионы», American Mathematical Monthly 88:42–5.
• Горенштейн, Д. (1980), Конечные группы , Нью-Йорк: Челси, ISBN  978-0-8284-0301-6 , МР   0569209
• Джонсон, Дэвид Л. (1980), Темы теории групповых презентаций , Cambridge University Press , ISBN  978-0-521-23108-4 , МР   0695161
• Ротман, Джозеф Дж. (1995), Введение в теорию групп (4-е изд.), Springer-Verlag, ISBN  978-0-387-94285-8
• П.Р. Жирар (1984) «Группа кватернионов и современная физика», Европейский журнал физики 5:25–32.
• Холл, Маршалл (1999), Теория групп (2-е изд.), Книжный магазин AMS, ISBN  0-8218-1967-4
• Курош, Александр Г. (1979), Теория групп , Книжный магазин AMS, ISBN  0-8284-0107-1

Внешние ссылки

• Вайсштейн, Эрик В. «Группа кватернионов» . Математический мир .
• Группы кватернионов в GroupNames
• Группа кватернионов в GroupProps
• Конрад, Кейт. «Обобщенные кватернионы»