Группы точек в трех измерениях

Выбранные группы точек в трех измерениях

Инволюционная симметрия С ) , (* [ ] =	Циклическая симметрия C нв , (*nn) [н] =	Двугранная симметрия Днх , (*n22) [п,2] =
Группа многогранников , [n,3], (*n32)
Тетраэдрическая симметрия Т д , (*332) [3,3] =	Октаэдрическая симметрия О х , (*432) [4,3] =	Икосаэдрическая симметрия I h , (*532) [5,3] =

В геометрии группа точек в трех измерениях — это группа изометрий в трех измерениях, оставляющая начало координат фиксированным, или, соответственно, группа изометрий сферы . Это подгруппа ортогональной группы O(3), группы всех изометрий , оставляющих начало координат фиксированным, или, соответственно, группы ортогональных матриц . O(3) сама по себе является подгруппой евклидовой группы E(3) всех изометрий.

Группы симметрии геометрических объектов являются группами изометрии. Соответственно, анализ групп изометрий — это анализ возможных симметрий . Все изометрии ограниченного (конечного) трехмерного объекта имеют одну или несколько общих неподвижных точек. Мы следуем обычному соглашению, выбирая начало координат в качестве одного из них.

Группу симметрии объекта иногда также называют его полной группой симметрии , в отличие от его собственной группы симметрии , пересечения его полной группы симметрии с E. ⁺ (3) , состоящее из всех прямых изометрий , т. е. изометрий, сохраняющих ориентацию . Для ограниченного объекта собственная группа симметрии называется группой вращения . Это пересечение его полной группы симметрии с SO(3) , полной группой вращения трехмерного пространства. Группа вращения ограниченного объекта равна его полной группе симметрии тогда и только тогда, когда объект является киральным .

Точечные группы, которые порождены исключительно конечным набором зеркальных плоскостей отражения, проходящих через одну и ту же точку, являются конечными группами Кокстера , представленными обозначением Кокстера .

Точечные группы в трех измерениях широко используются в химии , особенно для описания симметрии молекулы и молекулярных орбиталей, образующих ковалентные связи , и в этом контексте их также называют молекулярными точечными группами .

3D-изометрии, оставляющие начало координат фиксированным

См. Также: Евклидова группа § Обзор изометрий в трех измерениях.

Операции группы симметрии ( операции симметрии ) — это изометрии трёхмерного пространства R ³ которые оставляют начало координат фиксированным, образуя группу O(3). Эти операции можно разделить на:

• Прямые (сохраняющие ориентацию) операции симметрии, образующие группу SO(3):
  • Операция тождества, обозначаемая E единичной матрицей I. или
  • Поворот вокруг оси, проходящей через начало координат, на угол θ. Поворот на θ = 360°/ n для любого натурального числа n обозначается C _n (из обозначения Шенфлиса для группы C _n , которую он порождает ). Операция тождества, также обозначаемая C ₁ , является частным случаем оператора вращения.
• Косвенные (реверсивные) операции:
  • Инверсия, обозначаемая i или C _i . Матричное обозначение — −I .
  • Отражение в плоскости через начало координат обозначается σ.
  • Неправильное вращение , также называемое вращением-отражением: вращение вокруг оси на угол θ в сочетании с отражением в плоскости через начало координат, перпендикулярное оси. Вращение-отражение на θ = 360°/ n для любого натурального числа n обозначается S _n (из обозначения Шенфлиса для группы S _n , которую она порождает, если n четно).

Инверсия является частным случаем вращения-отражения (i = S ₂ ), как и отражение (σ = S ₁ ), поэтому эти операции часто считаются неправильными вращениями.

символу добавляется циркумфлекс Ĉ для обозначения оператора, как в Иногда к _n и Ŝ _n .

Сопряжение

При сравнении типа симметрии двух объектов начало координат выбирается для каждого отдельно, т.е. они не обязательно должны иметь один и тот же центр. При этом два объекта считаются принадлежащими одному и тому же типу симметрии, если их группы симметрии являются сопряженными подгруппами группы O(3) (две подгруппы H ₁ , H ₂ группы G сопряжены , если существует g ∈ G такой, что H ₁ = г ⁻¹ Н ₂ г ).

Например, два 3D-объекта имеют одинаковый тип симметрии:

• если оба имеют зеркальную симметрию, но относительно другой зеркальной плоскости
• если оба имеют 3-кратную вращательную симметрию, но относительно другой оси.

В случае нескольких зеркальных плоскостей и/или осей вращения две группы симметрии имеют один и тот же тип симметрии тогда и только тогда, когда существует вращение, отображающее всю структуру первой группы симметрии на структуру второй. (На самом деле таких вращений будет более одного, но не бесконечное число, как в случае, когда имеется только одно зеркало или ось.) Определение сопряжения также допускало бы зеркальное отображение структуры, но в этом нет необходимости, сама структура является ахиральным. Например, если группа симметрии содержит ось вращения третьего порядка, она содержит вращения в двух противоположных направлениях. (Структура хиральна для 11 пар пространственных групп с винтовой осью.)

Бесконечные группы изометрий

Смотрите также: Вращательная симметрия § Вращательная симметрия относительно любого угла

Существует множество бесконечных групп изометрий ; например, « циклическая группа » (это означает, что она порождается одним элементом – не путать с торсионной группой ), порожденная вращением на иррациональное количество оборотов вокруг оси. Мы можем создать нециклические абелевы группы , добавив больше вращений вокруг одной оси. Набор точек на окружности с рациональными числами градусов вокруг круга иллюстрирует группу точек, требующую бесконечного числа образующих . Существуют также неабелевы группы, порожденные вращением вокруг разных осей. Обычно это (в целом) свободные группы . Они будут бесконечными, если вращения не будут выбраны специально.

Все упомянутые до сих пор бесконечные группы не являются замкнутыми как топологические подгруппы группы O(3). Обсудим теперь топологически замкнутые подгруппы группы O(3).

Немаркированная сфера имеет симметрию O(3).

Весь O(3) представляет собой группу симметрии сферической симметрии ; SO(3) — соответствующая группа вращения. Другие бесконечные группы изометрии состоят из всех вращений вокруг оси, проходящей через начало координат, а также поворотов с дополнительным отражением в плоскостях, проходящих через ось, и/или отражением в плоскости, проходящей через начало координат, перпендикулярной оси. Группы с отражением в плоскостях, проходящих через ось, с отражением или без отражения в плоскости, проходящей через начало координат, перпендикулярное оси, являются группами симметрии для двух типов цилиндрической симметрии . Любая трехмерная фигура (подмножество R ³ ), обладающий бесконечной вращательной симметрией, также должен иметь зеркальную симметрию для каждой плоскости, проходящей через ось. Физические объекты, имеющие бесконечную вращательную симметрию, также будут иметь симметрию зеркальных плоскостей относительно оси, но векторные поля могут не иметь симметрии, например, векторы скорости конуса, вращающегося вокруг своей оси, или магнитное поле, окружающее провод.

Существует семь непрерывных групп, которые в некотором смысле являются пределами конечных групп изометрий. Эти так называемые предельные точечные группы или предельные группы Кюри названы в честь Пьера Кюри, который первым их исследовал. Семь бесконечных рядов осевых групп приводят к пяти предельным группам (две из них являются дубликатами), а семь оставшихся точечных групп дают еще две непрерывные группы. В международных обозначениях это список ∞, ∞2, ∞/м, ∞мм, ∞/мм, ∞∞ и ∞∞м. Не все это возможно для физических объектов, например, объекты с симметрией ∞∞ также обладают симметрией ∞∞m. Другие обозначения и более подробную информацию см. ниже.

Конечные группы изометрии

Симметрии в 3D, которые оставляют начало координат фиксированным, полностью характеризуются симметриями на сфере с центром в начале координат. Для конечных трехмерных точечных групп см. также сферические группы симметрии .

С точностью до сопряжения множество конечных трехмерных точечных групп состоит из:

• § Семь бесконечных серий осевых групп , которые имеют не более одной оси вращения более чем в 2 раза; это конечные группы симметрии на бесконечном цилиндре или, что то же самое, на конечном цилиндре. Иногда их называют осевыми или призматическими точечными группами.
• § Семь оставшихся точечных групп , которые имеют несколько осей вращения в 3 или более раз; эти группы также можно охарактеризовать как точечные группы, имеющие несколько осей трехкратного вращения. Возможные комбинации:
  • Четыре тройные оси (три симметрии T , Th _{тетраэдрические} и T _d )
  • и три оси 4-го порядка ( октаэдрические симметрии O и Oh _{Четыре оси 3-го порядка} )
  • Десять осей 3-го порядка и шесть осей 5-го порядка ( икосаэдрические симметрии I и I _h )

Согласно кристаллографической ограничительной теореме , только ограниченное число точечных групп совместимы с дискретной трансляционной симметрией : 27 из 7 бесконечных серий и 5 из 7 остальных. Вместе они составляют 32 так называемые кристаллографические точечные группы .

Семь бесконечных серий осевых групп

Бесконечный ряд осевых или призматических групп имеет индекс n , который может быть любым целым числом; в каждой серии n -я группа симметрии содержит n -кратную вращательную симметрию относительно оси, т.е. симметрию относительно поворота на угол 360°/ n . n =1 охватывает случаи отсутствия вращательной симметрии вообще. Есть четыре серии без других осей вращательной симметрии (см. Циклические симметрии ) и три с дополнительными осями 2-кратной симметрии (см. Двугранная симметрия ). Их можно понимать как группы точек в двух измерениях, протяженные с осевой координатой и отражениями в ней. Они относятся к группам фризов ; их можно интерпретировать как узоры из групп фризов, повторяющиеся n раз вокруг цилиндра.

В следующей таблице перечислены несколько обозначений для точечных групп: обозначение Германа-Могена (используется в кристаллографии ), обозначение Шёнфлиса (используется для описания молекулярной симметрии ), обозначение орбифолда и обозначение Кокстера . Последние три удобно связаны не только с ее свойствами, но и с порядком группы. Обозначение орбифолда — это унифицированное обозначение, также применимое для групп обоев и групп фризов . Кристаллографические группы имеют n, ограниченное 1, 2, 3, 4 и 6; удаление кристаллографического ограничения позволяет использовать любое положительное целое число.Серии:

Международный		Шенфлис	Орбифолд	Коксетер	Фриз	Структура.	Заказ	Пример	Комментарии
Даже н	Странный н				(цилиндр)
н		С н	пп	[н] +	п1	З н	н		n -кратная вращательная симметрия
2 н	н	С 2 н	n ×	[2 н + ,2 + ]	p11g	З 2 н	2 н		2 n -кратная роторно-отражательная симметрия
н /м	2 н	С н ч	н *	[н + ,2]	п11м	Z n ×Z 2	2 н
н мм	нм ​	С н в	* нн	[ н ]	п1м1	Дих н	2 н		Пирамидальная симметрия; по биологии, бирадиальная симметрия
№ 22	№ 2	Д н	22 н.	[ н ,2] +	стр.211	Дих н	2 н		Двугранная симметрия
2 н 2 м	нм ​	Д н д	2* н	[2н , 2 + ]	п2мг	Дих 2 н	4 n		Антипризматическая симметрия
н /ммм	2 н 2 м	Д н ч	*22 н.	[ н ,2]	п2мм	Dih n ×Z 2	4 n		Призматическая симметрия

Для нечетного n имеем Z _{2 n} = Z _n × Z ₂ и Dih _{2 n} = Dih _n × Z ₂ .

Группы Cn _и включая тривиальную C1 ₎ ( Dn _. киральны, остальные ахиральны

Термины «горизонтальный» (h) и «вертикальный» (v) и соответствующие индексы относятся к дополнительной плоскости зеркала, которая может быть параллельна оси вращения (вертикальная) или перпендикулярна оси вращения (горизонтальная).

Простейшие нетривиальные аксиальные группы эквивалентны абстрактной группе _Z2 :

• C _i (эквивалент S ₂ ) – инверсионная симметрия
• C ₂ – 2-кратная вращательная симметрия
• C _s (эквивалент C _1h и C _1v ) – отражательная симметрия , также называемая двусторонней симметрией .

Узоры на цилиндрической ленте, иллюстрирующие случай n = 6 для каждого из 7 бесконечных семейств точечных групп. Группа симметрии каждого рисунка – указанная группа.

Вторая из них является первой из одноосных групп ( циклических групп ) C _n порядка n (также применимых в 2D), которые генерируются одним поворотом на угол 360°/ n . В дополнение к этому можно добавить зеркальную плоскость, перпендикулярную оси, давая группу C _{n h} порядка 2 n , или набор из n зеркальных плоскостей, содержащих ось, давая группу C _{n v} также порядка 2 n. . Последняя является группой симметрии правильной n -сторонней пирамиды . Типичным объектом Cn _Dn или является _группы пропеллер . симметрии

Если добавить как горизонтальную, так и вертикальную плоскости отражения, их пересечения дают n осей вращения на 180°, поэтому группа больше не является одноосной. Эта новая группа порядка 4 n называется D _{n h} . Его подгруппой вращений является группа диэдра D _n порядка 2 n , которая все еще имеет оси вращения 2-го порядка, перпендикулярные главной оси вращения, но не имеет зеркальных плоскостей.

Примечание: в 2D D _n включает в себя отражения, которые также можно рассматривать как переворачивание плоских объектов без различия лицевой и обратной сторон; но в 3D эти две операции различаются: D _n содержит «переворачивание», а не отражения.

В этом семействе есть еще одна группа, называемая D _{n d} (или D _{n v} ), которая имеет вертикальные зеркальные плоскости, содержащие главную ось вращения, но вместо горизонтальной зеркальной плоскости имеет изометрию, сочетающую в себе отражение в горизонтальной плоскости и поворот на угол 180°/ n . D _{n h} — группа симметрии «правильной» n -угольной призмы , а также «правильной» n -угольной бипирамиды . D _{n d} — группа симметрии «правильного» n -угольного антипризмы , а также «правильного» n -угольного трапецоэдра . D _n — группа симметрии частично повернутой («скрученной») призмы.

Группы D ₂ и D _2h примечательны тем, что у них нет специальной оси вращения. Скорее, есть три перпендикулярные оси 2-го порядка. D ₂ — подгруппа всех полиэдральных симметрий (см. ниже), а — _{подгруппа} полиэдральных групп Th _D и Oh _2h . D ₂ встречается в таких молекулах, как твистан , и в гомотетрамерах, таких как конканавалин А. Элементы D ₂ находятся в соответствии 1-2 с вращениями, заданными единичными липшицевыми кватернионами .

Группа S _n создается комбинацией отражения в горизонтальной плоскости и поворота на угол 360°/n. Для нечетного n это равно группе, порожденной двумя отдельно, n _{h порядка} 2 n , и поэтому обозначение Sn _C не требуется; однако даже для n оно различно и имеет порядок n . Как и D _{n d,} он содержит ряд неправильных вращений, но не содержит соответствующих вращений.

Все группы симметрии в 7 бесконечных сериях различны, за исключением следующих четырех пар взаимно равных:

• C _1h и C _1v : группа порядка 2 с одиночным отражением ( C _s )
• D ₁ и C ₂ : группа порядка 2 с одним поворотом на 180°.
• D _1h и C _2v : группа порядка 4 с отражением в плоскости и поворотом на 180° через линию в этой плоскости.
• D _1d и C _2h : группа четвертого порядка с отражением в плоскости и поворотом на 180° через линию, перпендикулярную этой плоскости.

S ₂ — группа порядка 2 с одной инверсией ( C _i ).

Под «равным» здесь понимается то же самое с точностью до сопряжения в пространстве. Это сильнее, чем «с точностью до алгебраического изоморфизма». Например, существует три разные группы второго порядка в первом смысле, но во втором смысле только одна. Аналогично, например, S _{2 n} алгебраически изоморфен Z _{2 n} .

Группы могут быть построены следующим образом:

• С _н . Генерируется элементом, также называемым , _n который соответствует повороту на угол 2π/ Cn вокруг оси. Его элементами являются E (тождество), C _n , C _n ² , ..., С _н ^{п -1} , соответствующие углам поворота 0, 2π/ n , 4π/ n , ..., 2( n − 1)π/ n .
• С _{2 н} . Генерируется элементом C _{2 n} σ _h , где σ _h — отражение в направлении оси. Его элементами являются элементы C _n с C _{2 n} σ _h , C _{2 n} ³ σ _ч , ..., C _{2 n} ^{2 н -1} σ _ч добавил.
• С _{н ч} . Порождается элементом C _n и отражением σ _h . Его элементами являются элементы группы C _n с элементами σ _h , C _n σ _h , C _n ² σ _h , ..., C _n ^{п -1} σ _ч добавил.
• С _{н в} . Генерируется элементом C _n и отражением σ _v в направлении в плоскости, перпендикулярной оси. Его элементами являются элементы группы C _n с элементами σ _v , C _n σ _v , C _n ² σ _v , ..., C _n ^{п -1} σ _v добавил.
• Д _н . Создается элементом C _n и поворотом U = σ _h σ _v на 180° вокруг направления в плоскости, перпендикулярной оси. группы Cn _{Его элементами являются элементы} с элементами U Cn _U , Cn _, ² У, ..., С _н ^{п - 1} Вы добавили.
• Д _{н д} . Порождается элементами C _{2 n} σ _h и σ _v . Его элементами являются элементы группы C _n и дополнительные элементы S _{2 n} и C _{n v} , причем элементы C _{2 n} σ _h σ _v , C _{2 n} ³ σ _час σ _v , ..., C _{2 n} ^{2n − 1} σ _h σ _v добавлено.
• Д _{н ч} . Порождается элементами C _n , σ _h и σ _v . элементы Cn _и дополнительные Cnh _{элементы Dn} , Cnv _{Его элементами} и являются _. группы

Группы с непрерывным осевым вращением обозначаются знаком ∞ вместо n . Однако обратите внимание, что C _∞ здесь не то же самое, что бесконечная циклическая группа (также иногда обозначаемая C _∞ ), которая изоморфна целым числам. В следующей таблице представлены пять групп непрерывного осевого вращения. Они являются пределами конечных групп только в том смысле, что они возникают, когда основное вращение заменяется вращением на произвольный угол, то есть не обязательно на рациональное число градусов, как в случае с конечными группами. Физические объекты могут иметь только симметрию C _∞v или D _∞h , а векторные поля — другие.

Ч – М	Шенфлис	Орбифолд	Коксетер		Предел	Абстрактная группа
∞	C ∞	∞∞	[∞] +		С н	ТАК (2)
∞ , ∞/м	C ∞h	∞*	[2,∞ + ]		С н ч , С 2 н	ТАК(2)×Z 2
∞m	C ∞v	*∞∞	[∞]		С н в	О (2)
∞2	D ∞	22∞	[2,∞] +		Д н	О (2)
∞ м, ∞/мм	D ∞h	*22∞	[2,∞]		Д н ч , Д н д	О(2)×Z 2

Семь оставшихся точечных групп

Говорят, что остальные точечные группы обладают очень высокой или многогранной симметрией, поскольку они имеют более одной оси вращения порядка больше 2. Здесь C _n обозначает ось вращения на 360°/n, а S _n обозначает ось несобственного вращения. вращение через то же самое. На последовательных строках расположены обозначения орбифолда , обозначения Кокстера и диаграмма Кокстера , а также обозначения Германа-Могена (полные и сокращенные, если они отличаются) и порядок (количество элементов) группы симметрии. Группы:

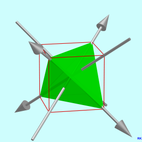
Т , (332) [3,3] + ( ) 23 заказать 12	киральная тетраэдрическая симметрия	Тройные оси вращения ( C 3 ) тетраэдра. Двойные оси вращения ( C 2 ) тетраэдра. Существует четыре оси C 3 , каждая через две вершины описанного куба (красный куб на изображениях) или через одну вершину правильного тетраэдра , и три оси C 2 через центры граней куба или середины граней куба. ребра тетраэдра. Эта группа изоморфна A группой 4 , знакопеременной группе из 4 элементов, и является вращения правильного тетраэдра. Это нормальная подгруппа T d , Th и октаэдрических симметрий. Элементы группы соответствуют 1 к 2 вращениям, заданным 24 единичными кватернионами Гурвица (« бинарная тетраэдрическая группа »).
Т д , (*332) [3,3] ( ) 4 3м заказать 24	полная тетраэдрическая симметрия	Зеркальная плоскость тетраэдра. Четырехкратная ось вращения-отражения ( S 4 ) тетраэдра. Эта группа является группой симметрии правильного тетраэдра . Эта группа имеет те же оси вращения, что и T , и оси C 2 теперь являются осями D 2d , тогда как четыре оси тройного порядка теперь дают начало четырем подгруппам C 3v . Эта группа имеет шесть зеркальных плоскостей, каждая из которых содержит два ребра куба или одно ребро тетраэдра, одну ось S 4 и две C 3 оси . T d изоморфна S 4 , симметричной группе из 4 букв, поскольку существует соответствие 1 к 1 между элементами T d и 24 перестановками четырех трехмерных осей. Объект симметрии C 3v относительно одной из осей 3-го порядка порождает под действием T d орбиту , состоящую из четырех таких объектов, и T d соответствует множеству перестановок этих четырех объектов. T d — нормальная подгруппа Oh группы . См. также изометрии правильного тетраэдра .
Т ч , (3*2) [3 + ,4] ( ) 2/ м3 , м3 заказать 24	пиритоэдрическая симметрия	Швы волейбольного мяча имеют симметрию T h . Эта группа имеет те же оси вращения, что и T , с зеркальными плоскостями, параллельными граням куба. Оси C 3 становятся осями S 6 , и возникает инверсионная симметрия. Двойные оси порождают три подгруппы D 2h . Th и изоморфна A 4 × Z 2 (так как T обе C i нормальные подгруппы), а не симметрической группе S 4 . Это симметрия куба, на каждой грани которого имеется отрезок линии, делящий грань на два равных прямоугольника, так что отрезки соседних граней не пересекаются на краях. Симметрии соответствуют четным перестановкам диагоналей тела и тому же в сочетании с инверсией. Это также симметрия пиритоэдра , который похож на описанный куб, в котором каждый прямоугольник заменен пятиугольником с одной осью симметрии, 4 равными сторонами и 1 разной стороной (той, которая соответствует отрезку линии, разделяющему грань куба); т. е. грани куба выпирают на разделительной линии и сужаются там. Это подгруппа (но не нормальная подгруппа) полной группы икосаэдрической симметрии (как группа изометрии, а не просто как абстрактная группа) с 4 из 10 осями 3-го порядка. Это обычная подгруппа Ой . ​Несмотря на то, что оно называется T h , оно не относится к тетраэдру.
О , (432) [4,3] + ( ) 432 заказать 24	киральная октаэдрическая симметрия	Эта группа подобна T , но оси C 2 теперь являются осями C 4 , а кроме того, через середины ребер куба проходят оси двукратного вращения, что дает начало трем подгруппам D 2 . Тройные оси теперь дают начало четырем D3 подгруппам . Эта группа также изоморфна S 4 , поскольку ее элементы находятся в 1-к-1 соответствии 24 перестановкам трехмерных осей, как и в случае T . Объект симметрии D 3 относительно одной из осей 3-го порядка порождает под действием О орбиту , состоящую из четырех таких объектов, причем О соответствует множеству перестановок этих четырех объектов. Это группа вращения куба и октаэдра . Представляя вращения с кватернионами , O состоит из 24 единичных кватернионов Гурвица и 24 липшицевых кватернионов с квадратом нормы 2, нормализованных путем деления на ${\sqrt {2}}$. Как и раньше, это переписка 1 к 2.
О х , (*432) [4,3] ( ) 4/м 3 2/м, м 3 м заказать 48	полная октаэдрическая симметрия	Эта группа имеет те же оси вращения, что и O плоскостями, содержащими обе зеркальные плоскости T d и Th , но с зеркальными . Тройные оси порождают четыре подгруппы D 3d . Три перпендикулярные оси четверного порядка O теперь дают подгруппы D 4h , а шесть осей двойного порядка дают шесть подгрупп D 2h . Эта группа изоморфна S 4 × Z 2 (поскольку O и C i являются нормальными подгруппами) и является группой симметрии куба и октаэдра . См. также изометрии куба .
Я , (532) [5,3] + ( ) 532 заказать 60	киральная икосаэдрическая симметрия	Это группа вращения икосаэдра и додекаэдра . Это нормальная подгруппа индекса I полной группе симметрий h 2 в . Группа содержит 10 версий D 3 и 6 версий D 5 (вращательные симметрии типа призм и антипризм). Он также содержит пять версий Т (см. Соединение пяти тетраэдров ). Группа I изоморфна из 5 букв , A поскольку ее 5 , знакопеременной группе элементы соответствуют 1 к 1 с четными перестановками пяти Т- симметрий (или пяти только что упомянутых тетраэдров). Представляя вращение с помощью кватернионов , I состоит из 120 единичных икосианов . Как и раньше, это переписка 1 к 2.
I h , (*532) [5,3] ( ) 5 3 2/м, 5 3 м заказать 120	полная икосаэдрическая симметрия	Это группа симметрии икосаэдра и додекаэдра. Группа I h изоморфна A 5 × Z 2, поскольку I и C i — нормальные подгруппы. Группа содержит 10 версий D 3d , 6 версий D 5d (симметрии типа антипризм) и 5 ​​версий T h .

Непрерывными группами, связанными с этими группами, являются:

• ∞∞, K или SO(3) — все возможные вращения.
• ∞∞m, K _h или O(3) — все возможные вращения и отражения.

Как отмечалось выше для бесконечных групп изометрий , любой физический объект, имеющий симметрию K, также будет иметь _{симметрию Kh} .

Светоотражающие группы Кокстера

Фундаментальные области 3D-групп Кокстера

А 3 , [3,3],	Б 3 , [4,3],	Н 3 , [5,3],
6 зеркал	3+6 зеркал	15 зеркал
2А 1 , [1,2],	3А 1 , [2,2],	А 1 А 2 , [2,3],
2 зеркала	3 зеркала	4 зеркала
А 1 , [1],	2А 1 , [2],	А2 , , [3]
1 зеркало	2 зеркала	3 зеркала

Группы отражающих точек в трех измерениях также называются группами Кокстера и могут быть заданы диаграммой Кокстера-Динкина и представляют собой набор зеркал, которые пересекаются в одной центральной точке. Обозначение Коксетера предлагает обозначения в квадратных скобках, эквивалентные диаграмме Кокстера, с символами разметки для групп точек вращения и других субсимметрий. обозначениях Шенфлиса отражающие точечные группы в 3D — Dnh _{и ,} и полные _{I. В} многогранные T , O Cnv это группы

Зеркальные плоскости ограничивают набор сферических треугольных областей на поверхности сферы. Группа Кокстера ранга n имеет n зеркальных плоскостей. Группы Кокстера, имеющие менее 3 генераторов, имеют вырожденные сферические треугольные домены, такие как лунки или полушария . В обозначениях Коксетера эти группы имеют тетраэдрическую симметрию [3,3], октаэдрическую симметрию [4,3], икосаэдрическую симметрию [5,3] и диэдрическую симметрию [p,2]. Число зеркал для неприводимой группы равно nh/2 , где h группы Кокстера — число Кокстера , n — размерность (3).

Вейль группа	Коксетер обозначение		Заказ	Коксетер число (час)	Зеркала (м)
Полиэдральные группы
AА3		[3,3]	24	4	6
BБ3		[4,3]	48	6	3+6
HH3		[5,3]	120	10	15
Диэдральные группы
2 А 1		[1,2]	4		1+1
3A3А1		[2,2]	8		2+1
Я 2 (п) А 1		[стр, 2]	4р		р+1
Циклические группы
2 А 1		[2]	4		2
Я 2 (п)		[п]	2р		п
Одиночное зеркало
А 1		[ ]	2		1

Группы ротации

Группами вращения, т. е. конечными подгруппами SO(3), являются: циклические группы C _n (группа вращения канонической пирамиды ), группы диэдра D _n (группа вращения равномерной призмы или канонической бипирамиды ), и группы вращения T , O и I правильного тетраэдра , октаэдра / куба и икосаэдра / додекаэдра .

В частности, группы диэдра D ₃ , D ₄ и т. д. являются группами вращения плоских правильных многоугольников, вложенных в трехмерное пространство, и такую ​​фигуру можно рассматривать как вырожденную правильную призму. Поэтому его еще называют диэдром (греч.: твердое тело с двумя гранями), что и объясняет название группы двугранников .

• Объект Cn _​ , Cnh _{, группу} , Cnv _{, группу} или S2n _{имеющий имеет} вращения Cn _. симметрии
• Объект, имеющий группу симметрии D _n , D _{n h} или D _{n d,} имеет группу вращения D _n .
• Объект, имеющий полиэдральную симметрию ( , T d _, Th , _T O , Oh , _или I , имеет в качестве группы I h ₎ вращения соответствующую группу без индекса: T , O или I .

Группа вращения объекта равна его полной группе симметрии тогда и только тогда, когда объект является киральным . Другими словами, киральными объектами являются объекты, группа симметрии которых находится в списке групп вращения.

заданные в нотациях Шёнфлиса , нотациях Кокстера , ( орбифолдных обозначениях Подгруппы вращения, ):

Отражение	Отражение/вращение	Неправильное вращение	Вращение
C n v , [n], (*nn)	C n h , [n + ,2], (n*)	С2н 2н , [ + ,2 + ], (n×)	С н , [н] + , (нн)
D n h , [2,n], (*n22)	Д н д , [2 + ,2n], (2*n)		Д н , [2,n] + , (n22)
Т д , [3,3], (*332)			Т , [3,3] + , (332)
О ч , [4,3], (*432)	Т ч , [3 + ,4], (3*2)		О , [4,3] + , (432)
I h , [5,3], (*532)			Я , [5,3] + , (532)

Соответствие между группами вращения и другими группами

Группы, содержащие инверсию

Группа вращения SO(3) является подгруппой O(3), полной группы вращения точки трехмерного евклидова пространства. Соответственно, O(3) является прямым произведением SO(3) и инверсии группы C _i (где инверсия обозначается ее матрицей − I ):

О (3) = ТАК (3) × { I , − I }

Таким образом, существует соответствие 1 к 1 между всеми прямыми изометриями и всеми косвенными изометриями посредством инверсии. Также существует соответствие 1 к 1 между всеми группами H прямых изометрий в SO(3) и всеми группами K изометрий в O(3), которые содержат инверсию:

К знак равно ЧАС × { я , - я }

Н = К ∩ SO(3)

изометрия ( A , I ) отождествляется с A. где

Для конечных групп соответствие следующее:

Группа вращения ЧАС	Паритет из н	Группа, содержащая инверсию К
С н	даже	С н ч
	странный	С 2 н
Д н	даже	Д н ч
	странный	Д н д
Т		Т ч
ТО		Ой ​
я		I h

Группы, содержащие косвенные изометрии, но без инверсии.

Если в группе прямых изометрий H есть подгруппа L индекса : 2, то существует соответствующая группа, содержащая косвенные изометрии, но не имеющая инверсии

M знак равно L ∪ ( ( ЧАС ∖ L ) × { - я } )

Например, H = C ₄ соответствует M = S ₄ .

Таким образом, M получается из H путем обращения изометрий в H ∖ L . Эта группа M , если ее рассматривать как абстрактную группу изоморфна H. , И наоборот, для всех точечных групп M , которые содержат косвенные изометрии, но не имеют инверсии, мы можем получить группу вращения H путем инвертирования косвенных изометрий.

Для конечных групп соответствие следующее:

Группа вращения ЧАС	Подгруппа Индекс-2 л	Паритет из н	Группа, содержащая непрямые изометрии М
С 2 н	С н	даже	С 2 н
		странный	С н ч
Д 2 н	Д н	даже	Д н ч
		странный	Д н д
Д н	С н	любой	С н в
ТО	Т		Т д

Нормальные подгруппы

В 2D циклическая группа -кратных k вращений . C _k является для каждого натурального числа k нормальной подгруппой O(2) и SO(2) Соответственно, в 3D для каждой оси циклическая группа k -кратных вращений вокруг этой оси является нормальной подгруппой группы всех вращений вокруг этой оси. Так как любая подгруппа индекса два нормальна, то группа вращений ( Cn ₎ нормальна как в группе ( Cnv _{плоскостей отражения через ее ось , )} , полученной добавлением к ( Cn ₎ в группе ( Cnh _{так и} ) получается добавлением к ( C _n ) плоскости отражения, перпендикулярной его оси.

Максимальные симметрии

Существуют две дискретные точечные группы, свойство которых состоит в том, что ни одна дискретная точечная группа не имеет их в качестве собственной подгруппы Oh _: и I _h . Их самая большая общая подгруппа — T _h . Две группы получаются из него путем замены 2-кратной вращательной симметрии на 4-кратную и добавления 5-кратной симметрии соответственно.

Существуют две кристаллографические точечные группы, свойство которых заключается в том, что ни одна кристаллографическая точечная группа не имеет их в качестве собственной подгруппы Oh _: и D _6h . Их максимальные общие подгруппы в зависимости от ориентации — D _3d и D _2h .

Группы, упорядоченные по типу абстрактной группы.

Ниже группы, описанные выше, упорядочены по типу абстрактной группы.

Наименьшими абстрактными группами, которые не являются какой-либо группой симметрии в 3D, являются группа кватернионов (порядка 8), Z ₃ × Z ₃ (порядка 9), дициклическая группа Dic ₃ (порядка 12) и 10 из 14 группы порядка 16.

В столбце «Количество элементов порядка 2» в следующих таблицах показано общее количество подгрупп изометрии типов C ₂ , C _i , C _s . Это общее число является одной из характеристик, помогающих различать различные типы абстрактных групп, а их тип изометрии помогает различать различные группы изометрии одной и той же абстрактной группы.

В рамках возможностей групп изометрии в 3D существует бесконечно много типов абстрактных групп с 0, 1 и 3 элементами порядка 2, есть две с 4 n + 1 элементами порядка 2 и три с 4 n + 3 элементами. порядка 2 (для каждого n ≥ 8). Никогда не бывает положительного четного числа элементов второго порядка.

Группы симметрии в 3D, циклические как абстрактная группа.

Группа симметрии кратной n вращательной симметрии — Cn _; - ее абстрактный тип группы — циклическая группа Zn _, обозначается Cn _{которая также} . Однако есть еще две бесконечные серии групп симметрии с этим абстрактным типом группы:

• Для четного порядка 2 n существует группа S _{2 n} (обозначение Шенфлиса), порожденная вращением на угол 180°/n вокруг оси в сочетании с отражением в плоскости, перпендикулярной оси. Для S ₂ обозначение C _i используется ; оно создается путем инверсии.
• Для любого порядка 2 n, где n нечетно, мы имеем C _{n h} ; он имеет ось вращения n -кратного порядка и перпендикулярную плоскость отражения. Он создается вращением на угол 360°/ n вокруг оси в сочетании с отражением. Для C _1h обозначение C _s используется ; он генерируется отражением в плоскости.

Таким образом, мы имеем (выделены жирным шрифтом 10 циклических кристаллографических точечных групп, к которым кристаллографическое ограничение применяется ):

Заказ	Группы изометрии	Абстрактная группа	# элементов порядка 2	Диаграмма цикла
1	С 1	З 1	0
2	С 2 , С я , С п	З 2	1
3	С 3	З 3	0
4	С 4 , С 4	З 4	1
5	С 5	ZZ5	0
6	С 6 , С 6 , С 3ч	Z 6 = Z 3 × Z 2	1
7	CС7	З 7	0
8	С 8 , С 8	З 8	1
9	С 9	З 9	0
10	С 10 , С 10 , С 5ч	Z 10 = Z 5 × Z 2	1

и т. д.

Группы симметрии в 3D, которые являются двугранными как абстрактная группа.

В 2D- диэдральную группу D _n входят отражения, которые также можно рассматривать как переворачивание плоских объектов без различия лицевой и обратной сторон.

Однако в 3D различаются две операции: группа симметрии, обозначаемая D _n, содержит n осей 2-го порядка, перпендикулярных оси n -го порядка, а не отражения. D _n — группа вращения призмы n- сторонней n с правильным основанием и n -сторонней бипирамиды с правильным основанием, а также правильной n -сторонней антипризмы и правильного - стороннего трапецоэдра . Группа также является полной группой симметрии таких объектов после того, как они стали хиральными , например, с помощью идентичной киральной маркировки на каждой грани или некоторой модификации формы.

Тип абстрактной группы — это диэдральная группа Dih _n , которая также обозначается D _n . Однако есть еще три бесконечные серии групп симметрии с этим абстрактным типом группы:

• Cnv _{. порядка} 2n , группа симметрии правильной n -сторонней пирамиды
• D _{n d} порядка 4 n , группа симметрии правильной n -сторонней антипризмы
• D _{n h} порядка 4 n для нечетных n . При n = 1 мы получаем D ₂ , уже рассмотренный выше, поэтому n ≥ 3.

Обратите внимание на следующее свойство:

Дих _{4 н +2} $\cong$ Dih _{2 n +1} × Z ₂

Таким образом, мы имеем, выделив 12 кристаллографических точечных групп жирным шрифтом и написав D _1d как эквивалент C _2h :

Заказ	Группы изометрии	Абстрактная группа	# элементов порядка 2	Диаграмма цикла
4	Д 2 , С 2в , С 2ч	Дих 2 = Z 2 × Z 2	3
6	Д3 , CС3в	Дих 3	3
8	Д 4 , С 4в , Д 2д	Это 4	5
10	Д 5 , С 5в	Дих 5	5
12	Д 6 , С 6в , Д 3д , Д 3ч	Дих 6 = Дих 3 × Z 2	7
14	D 7 , C 7v	Дих 7	7
16	Д 8 , С 8в , Д 4д	это 8	9
18	Д 9 , С 9в	День 9	9
20	Д 10 , С 10 в , Д 5ч , Д 5д	Дих 10 = Д 5 × Z 2	11

и т. д.

Другой

C _{2 n ,h} порядка 4 n имеет абстрактный групповой тип Z _{2 n} × Z ₂ . Для n = 1 мы получаем Dih ₂ , уже рассмотренный выше, поэтому n ≥ 2.

Таким образом, мы имеем, выделив жирным шрифтом две циклические кристаллографические точечные группы:

Заказ	Группа изометрии	Абстрактная группа	# элементов порядка 2	Диаграмма цикла
8	С 4 часа	З 4 × З 2	3
12	С 6 часов	Z 6 × Z 2 = Z 3 × Z 2 2 = Z3 × Dih2	3
16	С 8 часов	З 8 × З 2	3
20	С 10ч.	Z 10 × Z 2 = Z 5 × Z 2 2 = Z5 × Dih2	3

и т. д.

D _{n h} порядка 4 n имеет абстрактный групповой тип Dih _n × Z ₂ . Для нечетного n это уже рассмотрено выше, поэтому здесь мы имеем D _{2 n h} порядка 8 n , который относится к типу абстрактной группы Dih _{2 n} × Z ₂ ( n ≥1).

Таким образом, мы имеем, выделив жирным шрифтом 3 диэдральные кристаллографические точечные группы:

Заказ	Группа изометрии	Абстрактная группа	# элементов порядка 2	Диаграмма цикла
8	Д 2 часа	З 2 3	7
16	Д 4 часа	Дих 4 × Z 2	11
24	Д 6ч	Дих 6 × Z 2 = Дих 3 × Z 2 2	15
32	Д 8ч.	Дих 8 × Z 2	19

и т. д.

Остальные семь выделены жирным шрифтом 5 групп кристаллографических точек (см. Также выше):

Заказ	Группа изометрии	Абстрактная группа	# элементов порядка 2	Диаграмма цикла
12	Т	A 4	3
24	Т д , О	С 4	9
24	Т ч	А 4 × З 2	7
48	Ой ​	С 4 × З 2	19
60	я	AА5	15
120	I h	А 5 х Я 2	31

Фундаментальный домен

Триаконтаэдр Дисдякиса

Плоскости отражения икосаэдрической симметрии пересекают сферу по большим кругам с фундаментальными областями правого сферического треугольника.

Фундаментальной областью точечной группы является коническое тело . Объект с заданной симметрией в заданной ориентации характеризуется фундаментальной областью. Если объект является поверхностью, он характеризуется поверхностью в фундаментальной области, продолжающейся до ее радиальных бордальных граней или поверхности. Если копии поверхности не подходят, можно добавить радиальные грани или поверхности. Они подходят в любом случае, если фундаментальная область ограничена плоскостями отражения.

Для многогранника эта поверхность в фундаментальной области может быть частью произвольной плоскости. Например, в триаконтаэдре Дисдиакиса одна полная грань является фундаментальной областью икосаэдрической симметрии . Изменение ориентации плоскости дает различные возможности объединения двух или более соседних граней в одну, создавая различные другие многогранники с той же симметрией. Многогранник является выпуклым, если поверхность соответствует его копиям и радиальная линия, перпендикулярная плоскости, находится в фундаментальной области.

Также поверхность в фундаментальной области может состоять из нескольких граней.

Бинарные многогранные группы

Отображение Spin(3) → SO(3) представляет собой двойное покрытие группы вращения группой спинов в трех измерениях. (Это единственное связное покрытие SO(3), поскольку Spin(3) односвязен.)По теореме о решетке существует связь Галуа между подгруппами Spin(3) и подгруппами SO(3) (точечными группами вращения): образ подгруппы Spin(3) является точечной группой вращения, а прообраз точечная группа является подгруппой Spin(3). (Обратите внимание, что Spin(3) имеет альтернативные описания как специальную унитарную группу SU(2) и группу единичных кватернионов . Топологически эта группа Ли представляет собой трехмерную сферу S ³ .)

Прообраз конечной точечной группы называется бинарной группой многогранников , представленной как ⟨l,n,m⟩, и называется тем же именем, что и ее точечная группа, с префиксом бинарный , с двойным порядком соответствующей группы многогранников. (л, м, н). Например, прообразом группы икосаэдра (2,3,5) является бинарная группа икосаэдра , ⟨2,3,5⟩.

Бинарными многогранными группами являются:

• $A_{n}$: бинарная циклическая группа ( n + 1)-угольника порядка 2 n
• $D_{n}$: группа бинарных диэдра -угольника n , ⟨2,2, n ⟩, порядка 4 n
• $E_{6}$: бинарная тетраэдрическая группа , ⟨2,3,3⟩, порядок 24
• $E_{7}$: бинарная октаэдрическая группа , ⟨2,3,4⟩, порядок 48
• $E_{8}$: бинарная группа икосаэдра , ⟨2,3,5⟩, порядок 120

Они классифицируются по классификации ADE и фактору C ² действием бинарной группы многогранников является особенностью Дюваля .

Для групп точек, которые меняют ориентацию, ситуация более сложная, поскольку существует две группы контактов , поэтому существует две возможные двоичные группы, соответствующие данной группе точек.

Обратите внимание, что это покрытие групп, а не покрытие пространств — сфера односвязна и, следовательно, не имеет накрывающих пространств . Таким образом, не существует понятия «бинарный многогранник», охватывающего трехмерный многогранник. Бинарные многогранные группы являются дискретными подгруппами спиновой группы и при представлении спиновой группы действуют в векторном пространстве и могут стабилизировать многогранник в этом представлении - при отображении Spin (3) → SO (3) они действуют на тот же многогранник, на который действует основная (небинарная) группа, в то время как под представлениями спина или другими представлениями они могут стабилизировать другие многогранники.

В этом отличие от проективных многогранников : сфера покрывает проективное пространство (а также пространство линз ), и, таким образом, мозаика проективного пространства или пространства линз дает четкое представление о многограннике.

См. также

• Список сферических групп симметрии
• Список таблиц символов для химически важных групп трехмерных точек
• Группы точек в двух измерениях
• Группы точек в четырех измерениях
• Симметрия
• Изометрия евклидовой плоскости
• Групповое действие
• Группа точек
• Кристаллическая система
• Космическая группа
• Список малых групп
• Молекулярная симметрия

Ссылки

• Коксетер, HSM (1974), «7 бинарных многогранных групп», Правильные комплексные многогранники , Cambridge University Press, стр. 73–82 .
• Коксетер, HSM и Мозер, WOJ (1980). Генераторы и соотношения для дискретных групп, 4-е издание . Нью-Йорк: Springer-Verlag. ISBN  0-387-09212-9 . 6.5. Бинарные полиэдральные группы, с. 68
• Конвей, Джон Хортон ; Хьюсон, Дэниел Х. (2002), «Орбифолдная запись для двумерных групп», Structural Chemistry , 13 (3), Springer Нидерланды: 247–257, doi : 10.1023/A:1015851621002 , S2CID   33947139

Внешние ссылки

• Графический обзор 32 групп кристаллографических точек – образуют первые части (кроме пропуска n = 5) 7 бесконечных серий и 5 из 7 отдельных групп 3D точек.
• Обзор свойств групп точек
• Простейшие канонические многогранники каждого типа симметрии (использует Java)
• Точечные группы и кристаллические системы , И-Шу Вэй, стр. 4–6.
• Центр геометрии: 10.1 Формулы симметрии в декартовых координатах (трехмерные)