Эффект квантового зала
Квантовый эффект Холла (или целочисленный квантовый эффект Холла ) представляет собой квантованную версию эффекта Холла , который наблюдается в двумерных электронных системах, подверженных воздействию низких температур и сильных магнитных полей Холла , в которых сопротивление R xy демонстрирует ступеньки, которые принимают квантованные значения
где V Hall — напряжение Холла , I канал канала — ток , e — элементарный заряд и h — постоянная Планка . Делитель ν может принимать как целое ( ν = 1, 2, 3,... ), так и дробное ( ν = 1 / 3 , 2 / 5 , 3 / 7 , 2 / 3 , 3 / 5 , 1 / 5 , 2 / 9 , 3 / 13 , 5 / 2 , 12/5 . ) ,... значений Здесь ν примерно, но не точно равен коэффициенту заполнения уровней Ландау . Квантовый эффект Холла называется целым или дробным квантовым эффектом Холла в зависимости от того, является ли ν целым или дробным числом соответственно.
Яркой особенностью целочисленного квантового эффекта Холла является сохранение квантования (т.е. плато Холла) при изменении плотности электронов. Поскольку плотность электронов остается постоянной, когда уровень Ферми находится в чистой спектральной щели, эта ситуация соответствует той, где уровень Ферми представляет собой энергию с конечной плотностью состояний, хотя эти состояния локализованы (см. Локализация Андерсона ). [1]
Дробный квантовый эффект Холла более сложен и до сих пор считается открытой исследовательской проблемой. [2] Его существование фундаментально зависит от электрон-электронных взаимодействий. В 1988 году было высказано предположение о существовании квантового эффекта Холла без уровней Ландау . [3] Этот квантовый эффект Холла называется квантовым аномальным эффектом Холла (QAH). Существует также новая концепция квантового спинового эффекта Холла , которая является аналогом квантового эффекта Холла, при котором вместо токов заряда текут спиновые токи. [4]
Приложения
[ редактировать ]Стандарты электрического сопротивления
[ редактировать ]Квантование холловской проводимости ( ) обладает важным свойством чрезвычайной точности. [5] Было обнаружено, что фактические измерения проводимости Холла представляют собой целое или дробное число. e 2 / ч почти до одной миллиардной доли. Это позволило определить новый практический стандарт электрического сопротивления , основанный на кванте сопротивления, определяемом константой Клитцинга RK . фон Он назван в честь Клауса фон Клитцинга , первооткрывателя точного квантования. Квантовый эффект Холла также обеспечивает чрезвычайно точное независимое определение постоянной тонкой структуры — величины фундаментальной важности в квантовой электродинамике .
В 1990 году было определено фиксированное условное значение R K-90 = 25 812,807 Ом для использования при калибровке сопротивления во всем мире. [6] 16 ноября 2018 года 26-е заседание Генеральной конференции по мерам и весам решило установить точные значения h (константы Планка) и e (элементарного заряда), [7] замена обычного значения 1990 года точным постоянным значением (внутренним стандартом) R K = ч / е 2 = 25 812 ,807 45 ... Ой . [8]
Статус исследования
[ редактировать ]Дробный квантовый зал считается частью точного квантования . [9] Точное квантование в полной общности до конца не изучено, но его объясняют как очень тонкое проявление сочетания принципа калибровочной инвариантности с другой симметрией (см. Аномалии ). Вместо этого целочисленный квантовый зал считается решенной исследовательской задачей. [10] [11] и понимается в рамках формулы TKNN и лагранжианов Черна – Саймонса .
Дробный квантовый эффект Холла до сих пор считается открытой исследовательской проблемой. [2] Дробный квантовый эффект Холла можно также понимать как целочисленный квантовый эффект Холла, хотя и не для электронов, а для композитов заряд-поток, известных как составные фермионы . [12] Существуют и другие модели, объясняющие дробный квантовый эффект Холла. [13] В настоящее время это считается открытой исследовательской проблемой, поскольку не существует ни единого, подтвержденного и согласованного списка дробных квантовых чисел, ни единой согласованной модели, объясняющей их все, хотя такие утверждения существуют в области составных фермионов и неабелевых чисел Черна – Саймонса. Лагранжианы .
История
[ редактировать ]MOSFET металл -оксид-полупроводник ( полевой транзистор ), изобретенный Мохамедом Аталлой и Давоном Кангом в Bell Labs в 1959 году. [14] позволило физикам изучить поведение электронов в почти идеальном двумерном газе . [15] В МОП-транзисторе электроны проводимости перемещаются в тонком поверхностном слое, а напряжение « затвора » контролирует количество носителей заряда в этом слое. Это позволяет исследователям исследовать квантовые эффекты , эксплуатируя МОП-транзисторы высокой чистоты при температурах жидкого гелия . [15]
Целочисленное квантование холловской проводимости первоначально было предсказано исследователями Токийского университета Цунеей Андо, Юкио Мацумото и Ясутада Уэмура в 1975 году на основе приближенного расчета, в истинность которого они сами не верили. [16] В 1978 году исследователи из Университета Гакусюин Дзюнъити Вакабаяши и Синдзи Каваджи впоследствии наблюдали этот эффект в экспериментах, проведенных на инверсионном слое МОП-транзисторов. [17]
В 1980 году Клаус фон Клитцинг , работая в лаборатории сильных магнитных полей в Гренобле с образцами кремниевых МОП-транзисторов, разработанными Майклом Пеппером и Герхардом Дорда, сделал неожиданное открытие, что сопротивление Холла точно квантовано. [18] [15] За это открытие фон Клитцинг был удостоен Нобелевской премии по физике 1985 года . Связь между точным квантованием и калибровочной инвариантностью была впоследствии предложена Робертом Лафлином , который связал квантованную проводимость с квантованным переносом заряда в зарядовом насосе Таулесса. [11] [19] Большинство целочисленных квантовых экспериментов Холла в настоящее время проводится на арсенида галлия гетероструктурах , хотя можно использовать и многие другие полупроводниковые материалы. В 2007 году о целочисленном квантовом эффекте Холла было сообщено в графене при температурах, близких к комнатной. [20] а в магния -цинка оксиде ZnO–Mg x Zn 1– x O. [21]
Целочисленный квантовый эффект Холла
[ редактировать ]Уровни Ландау
[ редактировать ]В двух измерениях, когда классические электроны подвергаются воздействию магнитного поля, они следуют по круговым циклотронным орбитам. Когда система рассматривается квантовомеханически, эти орбиты квантуются. Для определения значений энергетических уровней необходимо решить уравнение Шрёдингера.
Поскольку система находится под действием магнитного поля, его необходимо ввести как электромагнитный векторный потенциал в уравнение Шрёдингера . Рассматриваемая система представляет собой электронный газ, который может свободно двигаться в направлениях x и y, но плотно удерживается в направлении z. Затем прикладывается магнитное поле в направлении z, и согласно калибровке Ландау электромагнитный векторный потенциал равен а скалярный потенциал . Таким образом, уравнение Шредингера для частицы с зарядом и эффективная масса в этой системе это:
где – канонический импульс, который заменяется оператором и это полная энергия.
Для решения этого уравнения можно разделить его на два уравнения, поскольку магнитное поле влияет только на движение по осям x и y. Тогда полная энергия становится суммой двух вкладов . Соответствующие уравнения по оси z:
Чтобы упростить задачу, решение рассматривается как бесконечная яма. Таким образом, решениями для направления z являются энергии , а волновые функции синусоидальные. Для и направлениях, решение уравнения Шредингера можно выбрать как произведение плоской волны в -направление с некоторой неизвестной функцией , то есть, . Это связано с тем, что векторный потенциал не зависит от и оператор импульса поэтому коммутирует с гамильтонианом. Подставив этот анзац в уравнение Шредингера, можно получить одномерное уравнение гармонического осциллятора с центром в точке .
где определяется как циклотронная частота и магнитная длина. Энергии:
- ,
А волновые функции движения в плоскости задаются произведением плоской волны в и полиномы Эрмита, ослабленные функцией Гаусса в , которые являются волновыми функциями гармонического осциллятора.
Из выражения для уровней Ландау видно, что энергия зависит только от , не на . государства с таким же но другой вырождаются.
Плотность штатов
[ редактировать ]В нулевом поле плотность состояний на единицу поверхности двумерного электронного газа с учетом спинового вырождения не зависит от энергии
- .
При включении поля плотность состояний схлопывается от постоянной до гребенки Дирака , серии Дирака функции, соответствующие уровням Ландау, разделенным . Однако при конечной температуре уровни Ландау приобретают ширину существование время между событиями рассеяния. Обычно предполагается, что точная форма уровней Ландау представляет собой профиль Гаусса или Лоренца .
Другая особенность состоит в том, что волновые функции образуют параллельные полосы в -направление, равномерно распределенное вдоль -ось, по линиям . Поскольку в любом направлении нет ничего особенного. -плоскости, если векторный потенциал был выбран иначе, должна быть найдена круговая симметрия.
Учитывая образец размеров и применяя периодические граничные условия в -направление существование целое число, можно получить, что каждый параболический потенциал имеет значение .
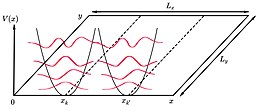
Количество состояний для каждого уровня Ландау и может быть рассчитана из отношения полного магнитного потока, проходящего через образец, к магнитному потоку, соответствующему состоянию.
Таким образом, плотность состояний на единицу поверхности равна
- .
Обратите внимание на зависимость плотности состояний от магнитного поля. Чем больше магнитное поле, тем больше состояний находится на каждом уровне Ландау. Как следствие, в системе возникает больше ограничений, поскольку занято меньше энергетических уровней.
Переписав последнее выражение как ясно, что каждый уровень Ландау содержит столько же состояний, сколько в 2DEG в .
Учитывая тот факт, что электроны являются фермионами , каждому состоянию, имеющемуся на уровнях Ландау, соответствуют два электрона, по одному электрону с каждым значением спина . . Однако если приложить большое магнитное поле, энергии расщепляются на два уровня из-за магнитного момента, связанного с выравниванием спина по магнитному полю. Разница в энергиях существование фактор, который зависит от материала ( для свободных электронов) и магнетон Бора . Знак берется, когда спин параллелен полю и когда оно антипараллельно. Этот факт, называемый спиновым расщеплением, означает, что плотность состояний на каждом уровне уменьшается вдвое. Обратите внимание, что пропорциональна магнитному полю, поэтому чем больше магнитное поле, тем более значимым является разделение.

Чтобы получить количество занятых уровней Ландау, определяют так называемый коэффициент заполнения. как отношение плотности состояний в 2ДЭГ к плотности состояний на уровнях Ландау.
В целом коэффициент заполнения не является целым числом. Оно оказывается целым числом, если имеется точное количество заполненных уровней Ландау. Вместо этого оно становится нецелым, если верхний уровень не полностью занят. В реальных экспериментах изменяют магнитное поле и фиксируют плотность электронов (а не энергию Ферми!) или изменяют плотность электронов и фиксируют магнитное поле. Оба случая соответствуют непрерывному изменению коэффициента заполнения и нельзя ожидать быть целым числом. С , при увеличении магнитного поля уровни Ландау перемещаются вверх по энергии, и число состояний на каждом уровне растет, поэтому меньше электронов занимают верхний уровень, пока он не станет пустым. Если магнитное поле будет продолжать увеличиваться, в конечном итоге все электроны окажутся на самом нижнем уровне Ландау ( ), и это называется магнитным квантовым пределом.
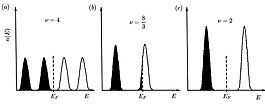
Продольное сопротивление
[ редактировать ]Фактор заполнения можно связать с удельным сопротивлением и, следовательно, с проводимостью системы. Когда является целым числом, энергия Ферми находится между уровнями Ландау, где нет состояний, доступных для носителей, поэтому проводимость становится равной нулю (считается, что магнитное поле достаточно велико, чтобы не было перекрытия между уровнями Ландау, в противном случае было бы электронов будет мало, а проводимость будет примерно ). Следовательно, удельное сопротивление также становится равным нулю (доказано, что в очень сильных магнитных полях продольная проводимость и удельное сопротивление пропорциональны). [22]
С проводимостью можно найти
Если продольное сопротивление равно нулю, а поперечное конечно, то . Таким образом, как продольная проводимость, так и удельное сопротивление становятся равными нулю.
Вместо этого, когда является полуцелым числом, энергия Ферми находится на пике распределения плотности некоторого Уровня Ландау. Это означает, что проводимость будет иметь максимум.
Такое распределение минимумов и максимумов соответствует «квантовым колебаниям», называемым осцилляциями Шубникова–де Гааза , которые становятся более актуальными по мере увеличения магнитного поля. Очевидно, что высота пиков тем больше, чем больше магнитное поле, поскольку плотность состояний увеличивается с увеличением поля, поэтому появляется больше носителей, которые вносят вклад в удельное сопротивление. Интересно отметить, что если магнитное поле очень мало, продольное сопротивление является постоянным, что означает, что достигается классический результат.
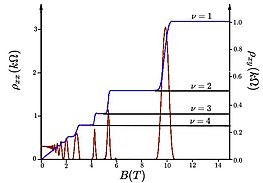
Поперечное удельное сопротивление
[ редактировать ]Из классического соотношения поперечного удельного сопротивления и замена находим квантование поперечного сопротивления и проводимости:
Тогда можно сделать вывод, что поперечное удельное сопротивление кратно обратному так называемому кванту проводимости. если коэффициент заполнения является целым числом. Однако в экспериментах плато наблюдаются для целых плато значений заполнения , что указывает на то, что между уровнями Ландау действительно существуют электронные состояния. Эти состояния локализуются, например, в примесях материала, где они захватываются орбитами и не могут вносить вклад в проводимость. Вот почему удельное сопротивление остается постоянным между уровнями Ландау. Опять же, если магнитное поле уменьшается, мы получаем классический результат, в котором удельное сопротивление пропорционально магнитному полю.
Фотонный квантовый эффект Холла
[ редактировать ]Квантовый эффект Холла, помимо наблюдаемого в двумерных электронных системах , можно наблюдать и в фотонах. Фотоны не обладают собственным электрическим зарядом , но посредством манипулирования дискретными оптическими резонаторами искусственное магнитное поле . и фазами связи или фазами на месте можно создать [23] [24] [25] [26] [27] Этот процесс можно выразить метафорой фотонов, прыгающих между несколькими зеркалами. Пропуская свет через несколько зеркал, фотоны направляются и получают дополнительную фазу, пропорциональную их угловому моменту . Это создает эффект, будто они находятся в магнитном поле .
Топологическая классификация
[ редактировать ]
Целые числа, возникающие при эффекте Холла, являются примерами топологических квантовых чисел . Они известны в математике как первые числа Черна и тесно связаны с фазой Берри . Яркой моделью, представляющей большой интерес в этом контексте, является модель Азбеля-Харпера-Хофштадтера, квантовая фазовая диаграмма которой представляет собой бабочку Хофштадтера, показанную на рисунке. Вертикальная ось — это сила магнитного поля , а горизонтальная ось — химический потенциал , фиксирующий электронную плотность. Цвета представляют целые проводимости Холла. Теплые цвета представляют собой положительные целые числа, а холодные цвета — отрицательные целые числа. Заметим, однако, что плотность состояний в этих областях квантованной холловской проводимости равна нулю; следовательно, они не могут создавать плато, наблюдаемые в экспериментах. Фазовая диаграмма фрактальна и имеет структуру во всех масштабах. На рисунке наблюдается явное самоподобие . При наличии беспорядка, являющегося источником наблюдаемых в экспериментах плато, эта диаграмма сильно меняется и фрактальная структура в основном размывается. Кроме того, в экспериментах контролируется фактор заполнения, а не энергия Ферми. Если эта диаграмма построена как функция коэффициента заполнения, все особенности полностью размыты, следовательно, она имеет очень мало общего с реальной физикой Холла.
Что касается физических механизмов, примеси и/или особые состояния (например, краевые токи) важны как для «целочисленных», так и для «дробных» эффектов. Кроме того, кулоновское взаимодействие также существенно в дробном квантовом эффекте Холла . Наблюдаемое сильное сходство между целочисленными и дробными квантовыми эффектами Холла объясняется тенденцией электронов образовывать связанные состояния с четным числом квантов магнитного потока, называемые составными фермионами .
Интерпретация атома Бора постоянной фон Клитцинга
[ редактировать ]Значение константы фон Клитцинга можно получить уже на уровне отдельного атома в рамках модели Бора, рассматривая это как одноэлектронный эффект Холла. В то время как при циклотронном движении по круговой орбите центробежная сила уравновешивается силой Лоренца, ответственной за поперечное индуцированное напряжение и эффект Холла, кулоновскую разность потенциалов в атоме Бора можно рассматривать как индуцированное одиночное напряжение Холла и периодическое движение электронов по окружности как ток Холла. Определение тока Холла отдельного атома как скорости заряда одного электрона. совершает Кеплеровские обороты с угловой частотой
и индуцированное напряжение Холла как разность кулоновского потенциала ядра водорода в точке орбиты электрона и на бесконечности:
Квантование определенного сопротивления Холла орбиты Бора можно получить по шагам постоянной фон Клитцинга как
которая для атома Бора линейна, но не обратна в целом числе n .
Релятивистские аналоги
[ редактировать ]Релятивистские примеры целочисленного квантового эффекта Холла и квантового спинового эффекта Холла возникают в контексте калибровочной теории решетки . [28] [29]
См. также
[ редактировать ]- Переходы квантового зала
- Дробный квантовый эффект Холла
- Квантовый аномальный эффект Холла
- Квантовые клеточные автоматы
- Композитные фермионы
- Проводимость Квантовая
- Эффект Холла
- датчик Холла
- Графен
- Квантовый спиновый эффект Холла
- Кулоновский потенциал между двумя токовыми петлями, помещенными в магнитное поле
Ссылки
[ редактировать ]- ^ От редакции (29 июля 2020 г.). «Квантовый эффект Холла продолжает раскрывать свои тайны математикам и физикам» . Природа . 583 (7818): 659. Бибкод : 2020Natur.583..659. . дои : 10.1038/d41586-020-02230-7 . ПМИД 32728252 .
- ^ Перейти обратно: а б Ханссон, TH (апрель 2017 г.). «Физика квантового зала: иерархии и методы конформной теории поля». Обзоры современной физики . 89 (25005): 025005. arXiv : 1601.01697 . Бибкод : 2017RvMP...89b5005H . doi : 10.1103/RevModPhys.89.025005 . S2CID 118614055 .
- ^ ФДМ Холдейн (1988). «Модель квантового эффекта Холла без уровней Ландау: реализация «аномалии четности» в конденсированном состоянии » . Письма о физических отзывах . 61 (18): 2015–2018. Бибкод : 1988PhRvL..61.2015H . doi : 10.1103/PhysRevLett.61.2015 . ПМИД 10038961 .
- ^ Эзава, Зюн Ф. (2013). Квантовые эффекты Холла: последние теоретические и экспериментальные разработки (3-е изд.). Всемирная научная. ISBN 978-981-4360-75-3 .
- ^ фон Клитцинг, Клаус (15 сентября 2005 г.). «Развитие квантового эффекта Холла» . Философские труды Королевского общества A: Математические, физические и технические науки . 363 (1834): 2203–2219. дои : 10.1098/rsta.2005.1640 . ISSN 1364-503X .
- ^ «Значение CODATA 2022: условное значение константы фон Клитцинга» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.
- ^ «Резолюции 26-й ГКМВ» (PDF) . БИПМ . Архивировано из оригинала (PDF) 19 ноября 2018 г. Проверено 19 ноября 2018 г.
- ^ «Значение CODATA 2022: константа фон Клитцинга» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.
- ^ Франц, Марсель (2010). «Во славу точного квантования» . Наука . 329 (5992): 639–640. дои : 10.1126/science.1194123 . ПМИД 20689008 . S2CID 206528413 .
- ^ «Лекция о Нобелевской премии Холдейна» (PDF) .
- ^ Перейти обратно: а б Р.Б. Лафлин (1981). «Квантованная холловская проводимость в двух измерениях». Физ. Преподобный Б. 23 (10): 5632–5633. Бибкод : 1981PhRvB..23.5632L . дои : 10.1103/PhysRevB.23.5632 .
- ^ Джайнендра, Джайн (19 апреля 2012 г.). Составные фермионы . Издательство Кембриджского университета. ISBN 978-1107404250 .
- ^ Тонг, Дэвид. «Квантовый эффект Холла» .
- ^ «1960 - Демонстрация металлооксидно-полупроводникового (МОП) транзистора» . Кремниевый двигатель . Музей истории компьютеров .
- ^ Перейти обратно: а б с Линдли, Дэвид (15 мая 2015 г.). «В центре внимания: ориентиры — случайное открытие ведет к стандарту калибровки» . Физика . 8 : 46. дои : 10.1103/физика.8.46 .
- ^ Цунея Андо; Юкио Мацумото; Ясутада Уэмура (1975). «Теория эффекта Холла в двумерной электронной системе». Дж. Физ. Соц. Япония . 39 (2): 279–288. Бибкод : 1975JPSJ...39..279A . дои : 10.1143/JPSJ.39.279 .
- ^ Дзюнъити Вакабаяси; Синдзи Каваджи (1978). «Эффект Холла в инверсионных слоях кремниевых МОП в сильных магнитных полях». Дж. Физ. Соц. Япония . 44 (6): 1839. Бибкод : 1978JPSJ...44.1839W . дои : 10.1143/JPSJ.44.1839 .
- ^ К. против Клитцинга; Г. Дорда; М. Пеппер (1980). «Новый метод высокоточного определения постоянной тонкой структуры на основе квантованного сопротивления Холла» . Физ. Преподобный Летт . 45 (6): 494–497. Бибкод : 1980PhRvL..45..494K . doi : 10.1103/PhysRevLett.45.494 .
- ^ Диджей Таулесс (1983). «Квантование транспорта частиц». Физ. Преподобный Б. 27 (10): 6083–6087. Бибкод : 1983PhRvB..27.6083T . дои : 10.1103/PhysRevB.27.6083 .
- ^ К.С. Новоселов; З. Цзян; Ю. Чжан; С.В. Морозов; Х.Л. Стормер; У. Цайтлер; Дж. К. Маан; Г.С. Бебингер; П. Ким; АК Гейм (2007). «Квантовый эффект Холла при комнатной температуре в графене». Наука . 315 (5817): 1379. arXiv : cond-mat/0702408 . Бибкод : 2007Sci...315.1379N . дои : 10.1126/science.1137201 . ПМИД 17303717 . S2CID 46256393 .
- ^ Цуказаки, А.; Отомо, А.; Кита, Т.; Оно, Ю.; Оно, Х.; Кавасаки, М. (2007). «Квантовый эффект Холла в полярных оксидных гетероструктурах» . Наука . 315 (5817): 1388–91. Бибкод : 2007Sci...315.1388T . дои : 10.1126/science.1137430 . ПМИД 17255474 . S2CID 10674643 .
- ^ Дэвис Дж.Х. Физика низких измерений . 6.4. Однородное магнитное поле; 6.5. Магнитное поле в узком канале. 6.6. Квантовый эффект Холла. ISBN 9780511819070 .
{{cite book}}: CS1 maint: местоположение ( ссылка ) - ^ Рагху, С.; Холдейн, FDM (23 сентября 2008 г.). «Аналоги краевых состояний квантового эффекта Холла в фотонных кристаллах» . Физический обзор А. 78 (3): 033834. arXiv : cond-mat/0602501 . Бибкод : 2008PhRvA..78c3834R . дои : 10.1103/PhysRevA.78.033834 . ISSN 1050-2947 . S2CID 119098087 .
- ^ Фанг, Кеджи; Ю, Цзунфу; Фань, Шаньхуэй (ноябрь 2012 г.). «Реализация эффективного магнитного поля для фотонов путем управления фазой динамической модуляции» . Природная фотоника . 6 (11): 782–787. Бибкод : 2012NaPho...6..782F . дои : 10.1038/nphoton.2012.236 . ISSN 1749-4885 . S2CID 33927607 .
- ^ Шайн, Натан; Рё, Альберт; Громов, Андрей; Соммер, Ариэль; Саймон, Джонатан (июнь 2016 г.). «Синтетические уровни Ландау для фотонов» . Природа . 534 (7609): 671–675. arXiv : 1511.07381 . Бибкод : 2016Natur.534..671S . дои : 10.1038/nature17943 . ISSN 0028-0836 . ПМИД 27281214 . S2CID 4468395 .
- ^ Миньков, Момчил; Савона, Винченцо (20 февраля 2016 г.). «Квантовый эффект Холдейна Холдейна для света в динамически модулированной решетке резонаторов» . Оптика . 3 (2): 200. arXiv : 1507.04541 . Бибкод : 2016Оптика...3..200М . дои : 10.1364/OPTICA.3.000200 . ISSN 2334-2536 . S2CID 1645962 .
- ^ Датт, Авик; Линь, Цянь; Юань, Луки; Миньков, Момчил; Сяо, Мэн; Фань, Шаньхуэй (03 января 2020 г.). «Единая фотонная полость с двумя независимыми физическими синтетическими измерениями» . Наука . 367 (6473): 59–64. arXiv : 1909.04828 . Бибкод : 2020Sci...367...59D . дои : 10.1126/science.aaz3071 . ISSN 0036-8075 . ПМИД 31780626 . S2CID 202558675 .
- ^ Д.Б. Каплан (1992). «Метод моделирования киральных фермионов на решетке». Письма по физике . Б288 (3–4): 342–347. arXiv : hep-lat/9206013 . Бибкод : 1992PhLB..288..342K . дои : 10.1016/0370-2693(92)91112-М . S2CID 14161004 .
- ^ МФЛ Гольтерман; К. Янсен; Д.Б. Каплан (1993). «Токи Черна – Саймонса и киральные фермионы на решетке». Письма по физике . Б301 (2–3): 219–223. arXiv : hep-lat/9209003 . Бибкод : 1993PhLB..301..219G . дои : 10.1016/0370-2693(93)90692-Б . S2CID 9265777 .
Дальнейшее чтение
[ редактировать ]- Доктор Йенни (1987). «Интегральный квантовый эффект Холла для неспециалистов». Преподобный Мод. Физ . 59 (3): 781–824. Бибкод : 1987РвМП...59..781Y . дои : 10.1103/RevModPhys.59.781 .
- Д. Се; Д. Цянь; Л. Рэй; Ю. Ся; Ю.С. Гор; Р. Дж. Кава; МЗ Хасан (2008). «Топологический изолятор Дирака в фазе Холла квантового спина». Природа . 452 (7190): 970–974. arXiv : 0902.1356 . Бибкод : 2008Natur.452..970H . дои : 10.1038/nature06843 . ПМИД 18432240 . S2CID 4402113 .
- 25 лет квантовому эффекту Холла , К. фон Клитцинг, Семинар Пуанкаре (Париж-2004). Постскриптум . PDF .
- Пресс-релиз Magnet Lab Квантовый эффект Холла наблюдался при комнатной температуре
- Аврон, Джозеф Э.; Осадчий, Даниил; Зайлер, Руди (2003). «Топологический взгляд на квантовый эффект Холла» . Физика сегодня . 56 (8): 38. Бибкод : 2003ФТ....56х..38А . дои : 10.1063/1.1611351 .
- Зюн Ф. Эзава: Квантовые эффекты Холла - теоретико-полевой подход и смежные темы. World Scientific, Сингапур, 2008 г., ISBN 978-981-270-032-2
- Санкар Д. Сарма, Арон Пинчук : Перспективы квантовых эффектов Холла. Wiley-VCH, Вайнхайм, 2004 г., ISBN 978-0-471-11216-7
- А. Баумгартнер; Т. Ин; К. Энсслин; К. Марановский; А. Госсард (2007). «Переход на эффекте квантового Холла в экспериментах со сканирующими воротами». Физ. Преподобный Б. 76 (8): 085316. Бибкод : 2007PhRvB..76h5316B . дои : 10.1103/PhysRevB.76.085316 .
- Е.И. Рашба , В.Б. Тимофеев, Квантовый эффект Холла, Сов. Физ. – Полупроводники, т. 20, стр. 617–647 (1986).






![{\displaystyle \left\{{\frac {1}{2m^{*}}}\left[\mathbf {p} -q\mathbf {A} \right]^{2}+V(z)\right \}\psi (x,y,z)=\varepsilon \psi (x,y,z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e35220a1ebb9bed3d0c8127c74b3467d8afdea6)




![{\displaystyle \left[-{\frac {\hbar ^{2}}{2m^{*}}}{\partial ^{2} \over \partial z^{2}}+V(z)\right ]u(z)=\varepsilon _{z}u(z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69b298c0ff7c211851461c359f2e20ccb8940135)








![{\displaystyle \left[- {\frac {\hbar ^{2}}{2m^{*}}}{\partial ^{2} \over \partial x^{2}}+{\frac {1} {2}}m^{*}\omega _{\rm {c}}^{2}(x-l_{B}^{2}k_{y})^{2}\right]u(x) =\varepsilon _{xy}u(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd0eac24c186b988302c8fd3cf4165677022af32)


























































