Пифагоров интервал

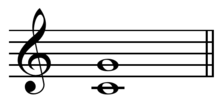
В музыкальной настройки теории пифагорейский интервал — это музыкальный интервал с соотношением частот , равным степени двойки, деленной на степень тройки, или наоборот . ^[1] Например, идеальная квинта с соотношением 3/2 (что эквивалентно 3 ¹/ 2 ¹) и идеальная кварта с соотношением 4/3 (что эквивалентно 2 ²/ 3 ¹) — интервалы Пифагора.

Все интервалы между нотами гаммы являются пифагорейскими, если они настроены по пифагорейской системе настройки . Однако некоторые пифагорейские интервалы используются и в других системах настройки. Например, упомянутые выше пифагорейские совершенные квинта и кварта также используются в простой интонации .

Таблица интервалов

Имя	Короткий	Другое имя (а)	Соотношение	Факторы	Вывод	центы	И центы	MIDI- файл	Пятые
уменьшенная секунда	d2		524288/531441	2 ¹⁹/3 ¹²		-23.460	0	играть ^ⓘ	-12
(идеальный) унисон	П1		1/1	3 ⁰/2 ⁰	1/1	0.000	0	играть ^ⓘ	0
Пифагорова запятая			531441/524288	3 ¹²/2 ¹⁹		23.460	0	играть ^ⓘ	12
второстепенная секунда	м2	клей , диатонический полутон, минорный полутон	256/243	2 ⁸/3 ⁵		90.225	100	играть ^ⓘ	-5
расширенный унисон	А1	апотом , хроматический полутон, мажорный полутон	2187/2048	3 ⁷/2 ¹¹		113.685	100	играть ^ⓘ	7
уменьшенная треть	д3	тон, целый тон, целый шаг	65536/59049	2 ¹⁶/3 ¹⁰		180.450	200	играть ^ⓘ	-10
главная секунда	М2	тон, целый тон, целый шаг	9/8	3 ²/2 ³	3·3/2·2	203.910	200	играть ^ⓘ	2
полудитон	m3	(пифагорейская минорная терция )	32/27	2 ⁵/3 ³		294.135	300	играть ^ⓘ	-3
дополненная секунда	А2		19683/16384	3 ⁹/2 ¹⁴		317.595	300	играть ^ⓘ	9
уменьшенная четвертая	d4		8192/6561	2 ¹³/3 ⁸		384.360	400	играть ^ⓘ	-8
дитон	M3	(пифагорейская мажорная терция )	81/64	3 ⁴/2 ⁶	27·3/32·2	407.820	400	играть ^ⓘ	4
идеальная четвертая	П4	диатессарон сесквитерций	4/3	2 ²/3	2·2/3	498.045	500	играть ^ⓘ	-1
дополненная треть	А3		177147/131072	3 ¹¹/2 ¹⁷		521.505	500	играть ^ⓘ	11
уменьшенная пятая часть	d5	тритон	1024/729	2 ¹⁰/3 ⁶		588.270	600	играть ^ⓘ	-6
дополненная четвертая	A4	тритон	729/512	3 ⁶/2 ⁹		611.730	600	играть ^ⓘ	6
уменьшенная шестая позиция	d6		262144/177147	2 ¹⁸/3 ¹¹		678.495	700	играть ^ⓘ	-11
идеальная пятая часть	П5	в движении другой половины	3/2	3 ¹/2 ¹	3/2	701.955	700	играть ^ⓘ	1
малая шестая	м6		128/81	2 ⁷/3 ⁴		792.180	800	играть ^ⓘ	-4
дополненная пятая часть	А5		6561/4096	3 ⁸/2 ¹²		815.640	800	играть ^ⓘ	8
уменьшенное седьмое место	d7		32768/19683	2 ¹⁵/3 ⁹		882.405	900	играть ^ⓘ	-9
мажорная шестая	М6		27/16	3 ³/2 ⁴	9·3/8·2	905.865	900	играть ^ⓘ	3
малая седьмая	м7		16/9	2 ⁴/3 ²		996.090	1000	играть ^ⓘ	-2
дополненная шестая	А6		59049/32768	3 ¹⁰/2 ¹⁵		1019.550	1000	играть ^ⓘ	10
уменьшенная октава	d8		4096/2187	2 ¹²/3 ⁷		1086.315	1100	играть ^ⓘ	-7
мажорная седьмая	М7		243/128	3 ⁵/2 ⁷	81·3/64·2	1109.775	1100	играть ^ⓘ	5
уменьшенная девятая	d9	(октава − запятая)	1048576/531441	2 ²⁰/3 ¹²		1176.540	1200	играть ^ⓘ	-12
(идеальная) октава	Р8	камертон	2/1		2/1	1200.000	1200	играть ^ⓘ	0
дополненная седьмая	A7	(октава + запятая)	531441/262144	3 ¹²/2 ¹⁸		1223.460	1200	играть ^ⓘ	12

Обратите внимание, что термины «дитон» и «полудитон» относятся к пифагорейской настройке, тогда как тон и тритон используются в целом для всех систем настройки. Несмотря на свое название, полудитон (3 полутона, или около 300 центов) вряд ли можно рассматривать как половину дитона (4 полутона, или около 400 центов).

Соотношение частот 144 интервалов в пифагорейской настройке на основе D. Названия интервалов даются в сокращенной форме. Чистые интервалы выделены **жирным** шрифтом. Интервалы Вольфа выделены красным. Числа больше 999 показаны как степени 2 или 3. Другие версии этой таблицы представлены здесь и здесь .

12-тональная пифагорейская шкала

В таблице показано, из каких нот некоторые из перечисленных выше интервалов можно сыграть на инструменте, использующем повторяющуюся 12-тоновую гамму (например, фортепиано), настроенном с помощью симметричной пифагорейской настройки на основе D. Более подробную информацию об этой таблице можно найти в разделе «Размер пифагорейских интервалов» .

Фундаментальные интервалы

Фундаментальными интервалами являются суперчастные отношения 2/1, 3/2 и 4/3. 2/1 — это октава или диапазон ( по-гречески «во всем»). 3/2 — это идеальная квинта , диапенте («через пять») или полуторный . 4/3 — это идеальная кварта , диатессарон («через четыре») или сесквитерций . Эти три интервала и их октавные эквиваленты, такие как совершенные одиннадцатая и двенадцатая, являются единственными абсолютными созвучиями пифагорейской системы. Все остальные интервалы имеют разную степень диссонанса: от плавного до грубого.

Разница между идеальной четвертой и идеальной квинтой заключается в тоне или мажорной секунде . Оно имеет соотношение 9/8, также известное как эпогдун , и это единственное другое суперчастное соотношение пифагорейской настройки, как показано в теореме Штормера .

Два тона составляют дитон , диссонансно широкую мажорную терцию , соотношение 81/64. Дитон отличается от основной трети (5/4) синтонной запятой (81/80). Точно так же разница между тоном и идеальной четвертью — это полудитон , узкая минорная терция , 32/27, которая отличается от 6/5 синтонной запятой. Эти различия «сглаживаются» или устраняются путем использования компромиссов в отношении одного темперамента .

Разница между второстепенной терцией и тоном составляет минорный полутон или лимму 256/243. Разница между тоном и лиммой - это основной полутон или апотом («отрезанная часть») 2187/2048. Хотя лимма и апотом представлены одной ступенью 12-тональной равной темперации , они не равны в пифагорейской настройке, и их разница, 531441/524288, известна как пифагорейская запятая .

Контраст с современной номенклатурой

Между названиями интервалов (количество ступеней шкалы + качество) и отношениями частот существует однозначное соответствие. Это контрастирует с равной темперацией, в которой интервалы с одинаковым соотношением частот могут иметь разные названия (например, уменьшенная квинта и увеличенная кварта); и с другими формами просто интонации, в которых одноимённые интервалы могут иметь разные соотношения частот (например, 9/8 для мажорной секунды от до до ре, но 10/9 для мажорной секунды от ре до ми).

См. также

Ссылки

^ Бенсон, Дональд К. (2003). Более гладкий камешек: математические исследования , стр.56. ISBN 978-0-19-514436-9 . «Отношение частот каждого интервала Пифагора представляет собой соотношение между степенью двойки и степенью тройки... что подтверждает требования Пифагора о том, что все интервалы должны быть связаны с отношениями целых чисел».

Внешние ссылки

Неоготическое использование Марго Шультер

[1] Бенсон, Дональд К. (2003). Более гладкий камешек: математические исследования , стр.56. ISBN 978-0-19-514436-9 . «Отношение частот каждого интервала Пифагора представляет собой соотношение между степенью двойки и степенью тройки... что подтверждает требования Пифагора о том, что все интервалы должны быть связаны с отношениями целых чисел».

[1]