Сходство (геометрия)

Чтобы узнать о других значениях, см. Сходство (значения) и Преобразование подобия (значения) .

Подобные цифры

В евклидовой геометрии два объекта подобны , если они имеют одинаковую форму или если один из них имеет ту же форму, что и зеркальное отображение другого. Точнее, одно можно получить из другого путем равномерного масштабирования (увеличения или уменьшения), возможно, с дополнительным перемещением , вращением и отражением . Это означает, что любой объект можно масштабировать, перемещать и отражать так, чтобы он точно совпадал с другим объектом. Если два объекта похожи, каждый из них соответствует результату определенного равномерного масштабирования другого.

Перевод

Вращение

Отражение

Масштабирование

Например, все круги подобны друг другу, все квадраты подобны друг другу и все равносторонние треугольники подобны друг другу. С другой стороны, не все эллипсы похожи друг на друга, не все прямоугольники похожи друг на друга и не все равнобедренные треугольники похожи друг на друга. Это связано с тем, что два эллипса могут иметь разное соотношение ширины и высоты, два прямоугольника могут иметь разное соотношение длины и ширины, а два равнобедренных треугольника могут иметь разные углы при основании.

Цифры, показанные одним цветом, похожи

Если два угла треугольника имеют меры, равные двум углам другого треугольника, то такие треугольники подобны. Соответствующие стороны подобных многоугольников пропорциональны, а соответствующие углы подобных многоугольников имеют одинаковую меру.

Две конгруэнтные фигуры подобны с масштабным коэффициентом 1. Однако некоторые школьные учебники специально исключают конгруэнтные треугольники из определения подобных треугольников, настаивая на том, что размеры должны быть разными, чтобы треугольники можно было квалифицировать как подобные.

Подобные треугольники

Два треугольника △ ABC и △ A'B'C' углы имеют одинаковую меру: это означает, что они подобны тогда и только тогда, когда длины соответствующих сторон пропорциональны подобны тогда и только тогда, когда соответствующие . Можно показать, что два треугольника, имеющие равные углы ( равноугольные треугольники ), подобны, то есть можно доказать, что соответствующие стороны пропорциональны. Это известно как теорема подобия AAA. Обратите внимание, что «ААА» — это мнемоника: каждая из трех букв «А» относится к «углу». Благодаря этой теореме некоторые авторы упрощают определение подобных треугольников, требуя только, чтобы соответствующие три угла были равны.

Существует несколько критериев, каждый из которых необходим и достаточен для того, чтобы два треугольника были подобны:

• Любые две пары углов равны, что в евклидовой геометрии означает, что все три угла равны:

Если ∠ BAC по мере равен ∠ B'A'C', а ∠ ABC по мере равен ∠ A'B'C', то из этого следует, что ∠ ACB по мере равен ∠ A'C'B' и треугольники подобны.

• Все соответствующие стороны пропорциональны:

$${\frac {\overline {AB}}{\overline {A'B'}}}={\frac {\overline {BC}}{\overline {B'C'}}}={\frac {\overline {AC}}{\overline {A'C'}}}.$$

Это эквивалентно тому, что один треугольник (или его зеркальное изображение) является увеличением другого.

• Любые две пары сторон пропорциональны, а углы, заключенные между этими сторонами, равны:

$${\frac {\overline {AB}}{\overline {A'B'}}}={\frac {\overline {BC}}{\overline {B'C'}}},\quad \angle ABC\cong \angle A'B'C'.$$

Это известно как критерий подобия SAS. «SAS» — это мнемоника: каждая из двух букв S относится к «стороне»; буква A означает «угол» между двумя сторонами.

Символически запишем сходство и различие двух треугольников △ ABC и △ A'B'C' следующим образом:

$${\begin{aligned}\triangle ABC&\sim \triangle A'B'C'\\\triangle ABC&\nsim \triangle A'B'C'\end{aligned}}$$

Есть несколько элементарных результатов, касающихся подобных треугольников в евклидовой геометрии:

• Любые два равносторонних треугольника подобны.
• Два треугольника, оба подобные третьему треугольнику, подобны друг другу ( транзитивность подобия треугольников).
• Соответствующие высоты подобных треугольников имеют то же соотношение, что и соответствующие стороны.
• Два прямоугольных треугольника подобны, если длины гипотенузы и другой стороны находятся в одинаковом соотношении. В этом случае имеется несколько эквивалентных условий, например, наличие у прямоугольных треугольников острого угла одной и той же меры или нахождение длин катетов (сторон) в одной и той же пропорции.

Учитывая треугольник △ ABC и отрезок DE, можно с помощью линейки и циркуля найти точку F такую, что △ ABC ~ △ DEF . Утверждение о существовании точки F, удовлетворяющей этому условию, является постулатом Уоллиса. и логически эквивалентен постулату параллельности Евклида . В гиперболической геометрии (где постулат Уоллиса неверен) подобные треугольники конгруэнтны.

В аксиоматической трактовке евклидовой геометрии, данной Джорджем Дэвидом Биркгофом (см. Аксиомы Биркгофа ), приведенный выше критерий подобия SAS использовался для замены как постулата параллельности Евклида, так и аксиомы SAS, которая позволила резко сократить аксиомы Гильберта .

Подобные треугольники служат основой для многих синтетических (без использования координат) доказательств в евклидовой геометрии. Среди элементарных результатов, которые можно доказать таким способом, можно выделить: теорему о биссектрисе угла , теорему о среднем геометрическом , теорему Чевы , теорему Менелая и теорему Пифагора . Подобные треугольники также составляют основу тригонометрии прямоугольного треугольника .

Другие подобные многоугольники

Подобные прямоугольники

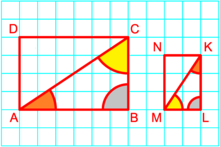
Понятие подобия распространяется на многоугольники , имеющие более трех сторон. Для любых двух подобных многоугольников соответствующие стороны, взятые в одной и той же последовательности (даже если по часовой стрелке для одного многоугольника и против часовой стрелки для другого), пропорциональны , а соответствующие углы, взятые в той же последовательности, равны по мере. Однако пропорциональность соответствующих сторон сама по себе недостаточна для доказательства подобия многоугольников вне треугольников (иначе, например, все ромбы были бы подобны). Точно так же равенства всех углов в последовательности недостаточно, чтобы гарантировать подобие (иначе все прямоугольники были бы подобны). Достаточным условием подобия многоугольников является пропорциональность соответствующих сторон и диагоналей.

Для заданного n все правильные n -угольники подобны.

Похожие кривые

Некоторые типы кривых обладают тем свойством, что все примеры этого типа похожи друг на друга. К ним относятся:

• Линии (любые две линии даже равны )
• Сегменты линий
• Круги
• Притчи
• Гиперболы определенного эксцентриситета
• Эллипсы определенного эксцентриситета
• Контактные сети
• Графики функции логарифма для разных оснований
• Графики показательной функции для разных базисов
• Логарифмические спирали самоподобны.

В евклидовом пространстве

Сходство действительное (также называемое преобразованием подобия или подобием ) евклидова пространства — это биекция f из пространства на себя, которая умножает все расстояния на одно и то же положительное число r , так что для любых двух точек x и y мы имеем

$d(f(x),f(y))=r\,d(x,y),$

где d ( x , y ) — евклидово расстояние от x до y . Скаляр ; r имеет много названий в литературе, в том числе коэффициент сходства , коэффициент растяжения и коэффициент сходства . Когда r = 1, подобие называется изометрией ( жестким преобразованием ). Два множества называются подобными , если одно является образом другого при сходстве.

В виде карты ⁠ $f:\mathbb {R} ^{n}\to \mathbb {R} ^{n},$⁠ подобие отношения r принимает вид

$f(x)=rAx+t,$

где ⁠ $A\in O^{n}(\mathbb {R} )$⁠ — размера n × n ортогональная матрица , а ⁠ $t\in \mathbb {R} ^{n}$⁠ — вектор трансляции.

Сходства сохраняют плоскости, линии, перпендикулярность, параллельность, средние точки, неравенства между расстояниями и отрезками линий. Сходства сохраняют углы, но не обязательно сохраняют ориентацию: прямые сходства сохраняют ориентацию, а противоположные сходства меняют ее.

Сходства евклидова пространства образуют группу при операции композиции, называемую сходств S. группой Прямые подобия образуют нормальную подгруппу S , а евклидова группа изометрий E ( n ) также образует нормальную подгруппу. Группа сходств S сама является подгруппой аффинной группы , поэтому каждое сходство является аффинным преобразованием .

Евклидову плоскость можно рассматривать как комплексную плоскость . то есть как двумерное пространство над реальными объектами . Преобразования двумерного подобия затем могут быть выражены в терминах комплексной арифметики и задаются формулой

• $f(z)=az+b$ (прямое подобие) и
• $f(z)=a{\overline {z}}+b$ (противоположные подобия),

где a и b — комплексные числа, a ≠ 0 . Когда | a |= 1 , эти сходства являются изометриями.

Соотношение площади и соотношение объемов

Мозаика большого треугольника показывает , что он похож на маленький треугольник с соотношением площадей 5. Коэффициент подобия равен ${\tfrac {5}{h}}={\tfrac {h}{1}}={\sqrt {5}}.$ Это можно использовать для построения непериодической бесконечной мозаики .

Основная статья: Закон квадрата-куба

Отношение площадей подобных фигур равно квадрату отношения соответствующих длин этих фигур (например, если сторону квадрата или радиус круга умножить на три, то его площадь умножится на девять — т.е. на три в квадрате). Высоты подобных треугольников находятся в том же отношении, что и соответствующие стороны. Если треугольник имеет сторону длины b и высоту, проведенную к этой стороне длины h , то аналогичный треугольник с соответствующей стороной длины kb будет иметь высоту, проведенную к этой стороне длины kh . Площадь первого треугольника равна $A={\tfrac {1}{2}}bh,$ а площадь подобного треугольника будет $$A'={\frac {1}{2}}\cdot kb\cdot kh=k^{2}A.$$Подобные фигуры, которые можно разложить на подобные треугольники, будут иметь одинаково связанные площади. Соотношения справедливы и для фигур, которые невозможно исправить.

Отношение объемов подобных фигур равно кубу отношения соответствующих длин этих фигур (например, при умножении ребра куба или радиуса сферы на три ее объем умножается на 27 — т.е. на три куба).

Закон квадрата-куба Галилея касается подобных твердых тел. Если отношение подобия (отношение соответствующих сторон) между твердыми телами равно k , то отношение площадей поверхностей твердых тел будет равно k. ² , а соотношение объемов будет k ³ .

Сходство с центром

Пример, где каждое сходство
сочинял сам с собой несколько раз подряд
имеет центр в центре правильного многоугольника , который сжимается.

Пример прямого подобия центра S
разлагается на поворот на угол 135°
и гомотетия, делящая площади пополам .

Примеры прямого сходства, имеющие у каждого свой центр .

Если сходство имеет ровно одну инвариантную точку : точку, которую сходство сохраняет неизменным, то эта единственная точка называется « центром » сходства.

На первом изображении под заголовком слева то или иное подобие сжимает правильный многоугольник в концентрический , вершины которого находятся каждая на стороне предыдущего многоугольника. Это вращательное сокращение повторяется , поэтому исходный многоугольник расширяется до бездны правильных многоугольников. Центром . подобия является общий центр последовательных многоугольников Красный отрезок соединяет вершину исходного многоугольника с его изображением по подобию, затем красный отрезок переходит к следующему изображению вершины и так далее, образуя спираль . На самом деле на этом первом изображении мы можем увидеть более трёх прямых подобий, потому что каждый правильный многоугольник инвариантен относительно определённых прямых подобий, точнее, определённых поворотов, центр которых является центром многоугольника, а композиция прямых подобий также является прямым сходство. Например, мы видим изображение исходного правильного пятиугольника при гомотетии отрицательного отношения –k , которое представляет собой подобие угла ±180° и положительного отношения, равного к .

Под заголовком справа на втором изображении показано сходство, разложенное на вращение и гомотетию. Подобие и поворот имеют одинаковый угол +135 градусов по модулю 360 градусов . Сходство и гомотетия имеют одинаковое соотношение ⁠ ${\tfrac {\sqrt {2}}{2}},$⁠ мультипликативное обратное отношение ⁠ ${\sqrt {2}}$⁠ ( квадратный корень из 2 ) обратного подобия. Точка S является общим центром трех преобразований: вращения, гомотетии и подобия. Например, точка W — это образ F при вращении, а точка T — это образ W при гомотетии, короче. $$T=H(W)=(R(F))=(H\circ R)(F)=D(F),$$назвав R , H и D предыдущим вращением, гомотетией и сходством, с буквой « D », как «Прямой».

Это прямое подобие, преобразующее треугольник △ EFA в треугольник △ ATB, можно разложить на вращение и гомотетию одного и того же центра S несколькими способами. Например, D = R ○ H = H ○ R , причем последнее разложение представлено только на изображении. Чтобы получить D, мы также можем в любом порядке составить поворот на угол –45° и гомотетию отношения ⁠ ${\tfrac {-{\sqrt {2}}}{2}}.$⁠

С « M » как «Зеркало» и « I » как «Непрямое», если M — отражение относительно линии CW , то M ○ D = I — это косвенное подобие, которое преобразует сегмент BF, как D, в сегмент CT , но преобразует точка Е в Б и точка А в А. сам Квадрат ACBT — это образ ABEF при подобии I отношения ⁠ ${\tfrac {1}{\sqrt {2}}}.$⁠ Точка A является центром этого подобия, поскольку любая точка K , инвариантная относительно нее, удовлетворяет $AK={\tfrac {AK}{\sqrt {2}}},$ возможно только если AK 0 , иначе пишется A = K. =

Как построить центр S прямого подобия D из квадрата ABEF , как найти точку S центра поворота на угол +135°, преобразующего луч ⁠ ${\overset {}{\overrightarrow {SE}}}$⁠ в луч ⁠ ${\overset {}{\overrightarrow {SA}}}$⁠ ? Это задача о вписанном угле плюс вопрос ориентации . Множество точек P таких, что ${\overset {}{{\overrightarrow {PE}},{\overrightarrow {PA}}=+135^{\circ }}}$ представляет собой дугу окружности EA , соединяющую E и A , из которых два радиуса, ведущие к E и A, образуют угол центральный 2 (180 ° – 135 °) = 2 × 45 ° = 90 ° . Этот набор точек представляет собой синюю четверть круга с центром F внутри квадрата ABEF . Таким же образом точка S является членом синей четверти круга с центром T внутри квадрата BCAT . Итак, точка S является точкой пересечения этих двух четвертей кругов.

В общих метрических пространствах

Треугольник Серпинского . Пространство, имеющее размерность самоподобия ${\tfrac {\log 3}{\log 2}}=\log _{2}3,$ что составляет примерно 1,58. (Из измерения Хаусдорфа .)

В общем метрическом пространстве ( X , d ) точным подобием является функция f из метрического пространства X в себя, которая умножает все расстояния на один и тот же положительный скаляр r , называемый коэффициентом сжатия f , так что для любых двух точек x и у нас есть

$$d(f(x),f(y))=rd(x,y).$$

В более слабых версиях подобия, например, функцией , f была бы билипшицевой а скаляр r — пределом.

$$\lim {\frac {d(f(x),f(y))}{d(x,y)}}=r.$$

Эта более слабая версия применяется, когда метрика представляет собой эффективное сопротивление топологически самоподобного множества.

Самоподобное подмножество метрического пространства ( X , d ) — это множество K , для которого существует конечное множество подобий { f _s } _{s ∈ S} с коэффициентами сжатия 0 ⩽ r _s < 1 такое, что K — единственный компакт подмножество X, для которого

Самоподобное множество, построенное по двум подобиям: ${\begin{aligned}z'&=0.1[(4+i)z+4]\\z'&=0.1[(4+7i)z^{*}+5-2i]\end{aligned}}$

$$\bigcup _{s\in S}f_{s}(K)=K.$$

Эти самоподобные множества имеют самоподобную меру µ ^Д с размерностью D, определяемой формулой

$$\sum _{s\in S}(r_{s})^{D}=1$$

множества которая часто (но не всегда) равна размерности Хаусдорфа и размерности упаковки . Если перекрытия между f _s ( K ) «небольшие», мы имеем следующую простую формулу для меры:

$$\mu ^{D}(f_{s_{1}}\circ f_{s_{2}}\circ \cdots \circ f_{s_{n}}(K))=(r_{s_{1}}\cdot r_{s_{2}}\cdots r_{s_{n}})^{D}.\,$$

Топология

В топологии метрическое пространство может быть построено путем определения сходства вместо расстояния . Сходство — это функция, значение которой тем больше, чем ближе две точки (в отличие от расстояния, которое является мерой несходства : чем ближе точки, тем меньше расстояние).

Определение сходства может варьироваться у разных авторов в зависимости от того, какие свойства желательны. Основными общими свойствами являются

1. Положительное определение:

$$\forall (a,b),S(a,b)\geq 0$$

1. В основном по сходству одного элемента сам с собой ( автоподобие ):

$$S(a,b)\leq S(a,a)\quad {\text{and}}\quad \forall (a,b),S(a,b)=S(a,a)\Leftrightarrow a=b$$

Можно вызвать дополнительные свойства, например:

• Отражательная способность : $\forall (a,b)\ S(a,b)=S(b,a),$ или
• Конечность : $\forall (a,b)\ S(a,b)<\infty .$

Верхнее значение часто устанавливается равным 1 (создавая возможность вероятностной интерпретации подобия).

Заметим, что в используемом здесь топологическом смысле сходство является своего рода мерой . Это использование отличается от преобразования подобия разделов § В евклидовом пространстве и § В общих метрических пространствах этой статьи.

Самоподобие

Самоподобие означает, что шаблон нетривиально подобен самому себе, например, набор чисел ..., 0,5, 0,75, 1, 1,5, 2, 3, 4, 6, 8, 12, ...}. { вида {2 ^я , 3·2 ^я } где я охватывает все целые числа. Когда это множество построено в логарифмическом масштабе, оно обладает одномерной трансляционной симметрией : прибавление или вычитание логарифма двух к логарифму одного из этих чисел дает логарифм другого из этих чисел. В самом заданном наборе чисел это соответствует преобразованию подобия, при котором числа умножаются или делятся на два.

Психология

Интуиция понятия геометрического подобия появляется уже у человеческих детей, что можно увидеть по их рисункам.

См. также

• Конгруэнтность (геометрия)
• Спиральное подобие
• Расстояние Хэмминга (сходство строк или последовательностей)
• Преобразование Гельмерта
• Инверсивная геометрия
• Индекс Жаккара
• Пропорциональность
• Основная теорема пропорциональности
• Семантическое сходство
• Поиск по сходству
• Сходство (философия)
• Пространство сходства в числовой таксономии
• Гомеоид (оболочка из концентрических подобных эллипсоидов)
• Решение треугольников

Ссылки

• Хендерсон, Дэвид В .; Тайминя, Дайна (2005). Опыт геометрии / евклидовой и неевклидовой истории с историей (3-е изд.). Пирсон Прентис-Холл. ISBN  978-0-13-143748-7 .
• Джейкобс, Гарольд Р. (1974). Геометрия . WH Freeman and Co. ISBN  0-7167-0456-0 .
• Педо, Дэн (1988) [1970]. Геометрия/Комплексный курс . Дувр. ISBN  0-486-65812-0 .
• Сибли, Томас К. (1998). Геометрическая точка зрения/Обзор геометрии . Аддисон-Уэсли. ISBN  978-0-201-87450-1 .
• Смарт, Джеймс Р. (1998). Современные геометрии (5-е изд.). Брукс/Коул. ISBN  0-534-35188-3 .
• Шталь, Саул (2003). Геометрия/От Евклида к узлам . Прентис-Холл. ISBN  978-0-13-032927-1 .
• Венема, Джерард А. (2006). Основы геометрии . Пирсон Прентис-Холл. ISBN  978-0-13-143700-5 .
• Йель, Пол Б. (1968). Геометрия и симметрия . Холден-Дэй.

Дальнейшее чтение

• Седерберг, Джудит Н. (2001) [1989]. «Глава 3.12: Преобразования подобия». Курс современной геометрии . Спрингер. стр. 183–189. ISBN  0-387-98972-2 .
• Коксетер, HSM (1969) [1961]. «§5 Подобие в евклидовой плоскости». стр. 67–76. «§7 Изометрия и подобие в евклидовом пространстве». стр. 96–104. Введение в геометрию . Джон Уайли и сыновья .
• Эвальд, Гюнтер (1971). Геометрия: Введение . Издательство Уодсворт . стр. 106, 181.
• Мартин, Джордж Э. (1982). «Глава 13: Сходства в плоскости». Геометрия преобразований: введение в симметрию . Спрингер. стр. 136–146. ISBN  0-387-90636-3 .

Внешние ссылки

• Анимированная демонстрация подобных треугольников
• Фундаментальная теорема подобия - наглядный набросок динамической геометрии.