Метод быстрых мультиполей на основе заряда граничных элементов

Зарядовая формулировка метода граничных элементов (МГЭ) представляет собой уменьшения размерности численный метод , который используется для моделирования квазистатических электромагнитных явлений в очень сложных проводящих средах (нацеленных, например, на человеческий мозг ) с очень большим (примерно до 1 миллиардов) число неизвестных. Зарядовый БЭМ решает интегральное уравнение теории потенциала записано через плотность индуцированного поверхностного заряда . Эта формулировка естественным образом сочетается с ускорением метода быстрых мультиполей (FMM), и весь метод известен как BEM-FMM на основе заряда . Комбинация БЭМ и ФММ является распространенным методом в различных областях вычислительной электромагнетики и в контексте биоэлектромагнетизма обеспечивает улучшения по сравнению с методом конечных элементов .

Историческое развитие

Наряду с более распространенным БЭМ, основанным на электрическом потенциале, В теории потенциала известна квазистатическая зарядовая БЭМ, полученная через плотность однослойного (заряда) для однокамерной среды. с начала 20 века. Для многокамерных проводящих сред формулировка поверхностной плотности заряда впервые появилась в дискретной форме (для фасетных интерфейсов) в статье Гелернтера и Свихарта 1964 года. Последующая непрерывная форма, включающая зависящие от времени и диэлектрические эффекты, появилась в статье Барнарда, Дака и Линн 1967 года. Зарядовая БЭМ также была разработана для проводящих, диэлектрических и магнитных сред. и используется в различных приложениях.

В 2009 году Грингард и др. успешно применил зарядовый БЭМ с быстрым мультипольным ускорением для молекулярной электростатики диэлектриков. Похожий подход к реалистичному моделированию человеческого мозга с множеством проводящих отделов был впервые описан Макаровым и др. на основе БЭМ в 2018 году. Наряду с этим, метод многоуровневых быстрых мультиполей нашел широкое применение в исследованиях радиолокации и антенн на СВЧ-частотах. так и в акустике.

Физическая основа – поверхностные заряды в биологических средах.

Зарядовый БЭМ основан на концепции приложенного (или первичного) электрического поля. $\mathbf {E} ^{i}$ и вторичное электрическое поле $\mathbf {E} ^{s}$. Импрессионное поле обычно известно априори или его найти тривиально. Для человеческого мозга воздействующее электрическое поле можно классифицировать как одно из следующих:

1. Консервативная сфера $\mathbf {E} ^{i}$ получено из воздействия плотности источников тока ЭЭГ или МЭГ в однородной бесконечной среде с проводимостью $\sigma$ в исходном местоположении;
2. Мгновенное соленоидальное поле $\mathbf {E} ^{i}$ индукционной катушки, полученной на основе закона индукции Фарадея в однородной бесконечной среде (воздухе), когда транскраниальной магнитной стимуляции (ТМС); речь идет о задачах
3. Поверхностное поле $\mathbf {E} ^{i}$полученный из приложенной поверхностной плотности тока $\mathbf {J} ^{i}=\sigma \mathbf {E} ^{i}$ токовых электродов, инжектирующих электрический ток на границу отсека с проводимостью $\sigma$ когда речь идет о транскраниальной стимуляции постоянным током (tDCS) или глубокой стимуляции мозга (DBS);
4. Консервативная сфера $\mathbf {E} ^{i}$ зарядов, осаждаемых на электродах напряжения для tDCS или DBS. Эта конкретная проблема требует комплексного решения, поскольку эти расходы будут зависеть от окружающей среды;
5. Применительно к многомасштабному моделированию поле $\mathbf {E} ^{i}$ полученное из любого другого макроскопического численного решения в небольшой (мезомасштабной или микромасштабной) пространственной области мозга. Например, можно использовать постоянное поле.

   

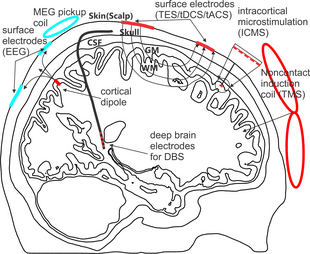
   Примеры воздействия электрического поля для стимуляции мозга ( TMS / DBS / tDCS / ICMS ) и нейрофизиологических записей (ЭЭГ / МЭГ ). WM – белое вещество, GM – серое вещество и CSF – спинномозговая жидкость.

При «включении» приложенного поля свободные заряды , находящиеся внутри проводящего объема D, же начинают перераспределяться и накапливаться на границах (границах) областей различной проводимости в D. сразу Поверхностная плотность заряда $\rho (\mathbf {r} )$ появляется на границах раздела проводимости. Эта плотность заряда индуцирует вторичное консервативное электрическое поле. $\mathbf {E} ^{s}$ следуя закону Кулона .

Одним из примеров является человек, находящийся под линией электропередачи постоянного тока с известным полем. $\mathbf {E} ^{i}$ направлен вниз. Верхняя поверхность проводящего тела человека будет заряжена отрицательно, а нижняя часть - положительно. Эти поверхностные заряды создают вторичное электрическое поле, которое эффективно нейтрализует или блокирует первичное поле повсюду в теле, так что ток не течет внутри тела в условиях устойчивого состояния постоянного тока.

Другой пример — человеческая голова с прикрепленными электродами. На любой границе проводимости с нормальным вектором $\mathbf {n}$ указание из «внутреннего» (-) отсека проводимости $\sigma ^{-}$во «внешний» (+) отсек проводимости $\sigma ^{+}$, закон тока Кирхгофа требует непрерывности нормальной составляющей плотности электрического тока. Это приводит к межфазному граничному условию в виде

$\sigma ^{+}\mathbf {E} ^{+}\cdot \mathbf {n} =\sigma ^{-}\mathbf {E} ^{-}\cdot \mathbf {n}$

для каждого аспекта триангулированного интерфейса. Пока $\sigma ^{\pm }$ отличаются друг от друга, две нормальные компоненты электрического поля, $\mathbf {E} ^{\pm }\cdot \mathbf {n}$, тоже должно быть разным. Такой переход через интерфейс возможен только в том случае, если на этом интерфейсе существует слой поверхностного заряда. Таким образом, если приложить электрический ток или напряжение, изменится плотность поверхностного заряда.

Цель численного анализа — найти неизвестное распределение поверхностного заряда и, следовательно, общее электрическое поле. $\mathbf {E} =\mathbf {E} ^{i}+\mathbf {E} ^{s}$ (и общий электрический потенциал , если требуется) в любой точке космоса.

Вывод дискретного БЭМ-ФММ с использованием закона Гаусса и закона Кулона. Закон Гаусса, примененный к «таблетке», расположенной на m -й грани, можно использовать (в сочетании с законом Кулона, применимым ко всем остальным граням), чтобы дать аппроксимацию электрического поля внутри и снаружи каждой грани.

Система уравнений для поверхностных зарядов

Ниже дан вывод на основе закона Гаусса и закона Кулона . Все границы раздела проводимости, обозначаемые S , дискретизированы на плоские треугольные грани. $t_{m}$ с центрами $\mathbf {r} _{m}$. Предположим, что m -я грань с вектором нормали $\mathbf {n} _{m}$ и площадь $A_{m}$ имеет равномерную поверхностную плотность заряда $\rho _{m}$. Если бы присутствовала объемная тетраэдрическая сетка, заряженные грани принадлежали бы тетраэдрам с разными значениями проводимости. Сначала мы вычисляем электрическое поле $\mathbf {E} _{m}^{+}$ в точку $\mathbf {r} _{m}+\delta \mathbf {n} _{m}$, для $\delta \rightarrow 0^{+}$ т. е. сразу за внешней гранью 𝑚 в ее центре. Это поле содержит три вклада:

• Непрерывное приложенное электрическое поле $\mathbf {E} ^{i}$ сам;
• Электрическое поле самой m -й заряженной грани. Очень близко к грани его можно аппроксимировать как электрическое поле бесконечного слоя с однородным поверхностным зарядом. $\rho _{m}$. По закону Гаусса оно определяется выражением $+\rho _{m}/2\varepsilon _{0}\cdot \mathbf {n} _{m}$ где $\varepsilon _{0}$ – фоновая электрическая проницаемость;
• Электрическое поле, создаваемое всеми остальными гранями $t_{n}$, которые мы аппроксимируем как точечные заряды $A_{n}\rho _{n}$ в каждом центре $\mathbf {r} _{n}$.

Аналогичная трактовка справедлива и для электрического поля. $\mathbf {E} _{m}^{-}$ только внутри грани 𝑚, но электрическое поле плоского слоя заряда меняет знак. Использование закона Кулона для расчета вклада граней, отличных от $t_{m}$, мы находим

$\mathbf {E} _{m}^{\pm }=\pm {\frac {\rho _{m}}{2\varepsilon _{0}}}\mathbf {n} _{m}+\sum _{n=1;n\neq m}^{M}{\frac {\rho _{n}}{4\pi \varepsilon _{0}}}{\frac {\mathbf {r} _{m}-\mathbf {r} _{n}}{|\mathbf {r} _{m}-\mathbf {r} _{n}|^{3}}}+\mathbf {E} ^{i}(\mathbf {r} _{m}),\ m=1,2,\dots ,M$

Из этого уравнения мы видим, что нормальная компонента электрического поля действительно совершает скачок через заряженную границу раздела. Это эквивалентно соотношению скачка теории потенциала. На втором этапе два выражения для $\mathbf {E} _{m}^{\pm }$ подставляются в межфазное граничное условие $\sigma ^{-}\mathbf {E} _{m}^{-}\cdot \mathbf {n} _{m}=\sigma ^{+}\mathbf {E} _{m}^{+}\cdot \mathbf {n} _{m}$, применимо к каждому аспекту 𝑚. Эта операция приводит к системе линейных уравнений для неизвестных плотностей заряда $\rho _{m}$ который решает проблему:

$\rho _{m}=K_{m}\mathbf {n} _{m}\cdot \underbrace {\sum _{n=1;n\neq m}^{M}{\frac {\rho _{n}}{2\pi }}{\frac {\mathbf {r} _{m}-\mathbf {r} _{n}}{|\mathbf {r} _{m}-\mathbf {r} _{n}|^{3}}}} +{2}\varepsilon _{0}K_{m}\mathbf {n} _{m}\cdot \mathbf {E} ^{i}(\mathbf {r} _{m}),\ m=1,2,\dots ,M$

где $K_{m}={\frac {\sigma ^{-}-\sigma ^{+}}{\sigma ^{-}+\sigma ^{+}}}$ – контраст электропроводности на m -й грани. Константа нормализации $\varepsilon _{0}$ сократится после подстановки решения в выражение для $\mathbf {E} ^{s}$ и становится лишним.

Применение метода быстрых мультиполей

Для современных характеристик топологий мозга с постоянно растущим уровнем сложности приведенная выше система уравнений для $\rho _{m}$ очень большой; поэтому она решается итеративно. Первоначальное предположение о $\rho _{m}$ является последним членом в его правой части, а сумма игнорируется. Затем вычисляется сумма, уточняется первоначальное предположение и т. д. Это решение использует простой итерационный метод Якоби . Более строгий обобщенный метод минимальной невязки (GMRES) обеспечивает гораздо более быструю сходимость BEM-FMM. В любом случае основная работа заключается в вычислении суммы в фигурных скобках в приведенной выше системе уравнений для каждого ${m}$ на каждой итерации; эта операция соответствует повторяющемуся умножению матрицы на вектор. Однако эту сумму можно признать электрическим полем (раз ${\frac {1}{2\pi \epsilon _{0}}}$) из ${M}$ расходы, подлежащие расчету в ${M}$ наблюдательные пункты. Такое вычисление и является задачей метода быстрых мультиполей , выполняющего быстрое умножение матрицы на вектор в $O(M\log {M})$ или даже $O(M)$ операции вместо $O(M^{2})$. Библиотека FMM3D реализованные как на Python , так и на MATLAB для этой цели можно использовать . Поэтому нет необходимости формировать или хранить плотную системную матрицу, типичную для стандартной БЭМ .

БЭМ непрерывного заряда. Коррекция ближнего поля

Сформулированная выше система уравнений получена методом коллокации и является менее точной. Соответствующее интегральное уравнение получается из соотношений локального скачка теории потенциала и локальное межфазное граничное условие нормальной непрерывности электрического тока. Это интегральное уравнение Фредгольма второго рода.

$\rho (\mathbf {r} )=K(\mathbf {r} )\mathbf {n} (\mathbf {r} )\cdot \int _{S}{\frac {\rho (\mathbf {r^{\prime }} )}{2\pi }}{\frac {\mathbf {r} -\mathbf {r^{\prime }} }{|\mathbf {r} -\mathbf {r^{\prime }} |^{3}}}ds(\mathbf {r^{\prime }} )+2\varepsilon _{0}K(\mathbf {r} )\mathbf {E} ^{i}(\mathbf {r} )\cdot \mathbf {n} (\mathbf {r} ),\mathbf {r} {\text{ on }}S$

Его вывод не требует тождеств Грина (интегрирования по частям) и применим к невложенным геометриям. Когда метод Галеркина и на триангулированных интерфейсах по-прежнему используются те же базисные функции нулевого порядка (с постоянной плотностью заряда для каждой грани), мы получаем точно такую ​​же дискретизацию, как и раньше, если заменить двойные интегралы по поверхностям применяется $S_{m}$ и $S_{n}$ треугольников $t_{m}$ и $t_{n}$соответственно, по

$\int _{S_{m}}\int _{S_{n}}{\frac {\mathbf {r} -\mathbf {r^{\prime }} }{|\mathbf {r} -\mathbf {r^{\prime }} |^{3}}}ds(\mathbf {r^{\prime }} )ds(\mathbf {r} )\approx {A_{m}}{A_{n}}{\frac {\mathbf {r} _{m}-\mathbf {r} _{n}}{|\mathbf {r} _{m}-\mathbf {r} _{n}|^{3}}},$

где ${A_{n}}$ площадь поверхности треугольника ${t_{n}}$. Это приближение справедливо только тогда, когда $|\mathbf {r} _{m}-\mathbf {r} _{n}|$ намного больше типичного размера грани, т. е. находится в «дальнем поле». В противном случае полуаналитические формулы и квадратуры Гаусса для треугольников следует использовать . Обычно от 4 до 32 таких соседних интегралов на фасет должны быть предварительно вычислены, сохранены и затем использованы на каждой итерации. Это важная поправка к методу простых быстрых мультиполей в «ближнем поле», который также следует использовать в простой дискретной формулировке, полученной выше. Такая коррекция позволяет получить неограниченное числовое (но не анатомическое) разрешение в мозге.

Приложения и ограничения

Применение зарядового БЭМ-ФММ включает моделирование стимуляции мозга. с точными расчетами TMS практически в реальном времени а также нейрофизиологические записи. Они также включают моделирование сложных мезомасштабных топологий головы, таких как тонкие мембраны мозга. ( твердая мозговая оболочка , паутинная оболочка и мягкая мозговая оболочка ). Это особенно важно для точного прогнозирования доз транскраниальной стимуляции постоянным током и электросудорожной терапии . BEM-FMM позволяет выполнять простое адаптивное уточнение сетки, включая несколько экстрацеребральных отделов мозга. Другое применение — моделирование возмущений электрического поля внутри плотно упакованной ветви нейронов/аксонов. Такие возмущения изменяют биофизическую активирующую функцию . Формулировка БЭМ на основе заряда разрабатывается для многообещающего двухдоменного биофизического моделирования аксональных процессов.

В своем нынешнем виде зарядовый БЭМ-ФММ применим только к многокамерным кусочно-однородным средам; он не может справиться с макроскопически анизотропными тканями. Кроме того, максимальное количество граней (степеней свободы) ограничено примерно $10^{9}$ для типичных ресурсов академического компьютерного оборудования, используемых по состоянию на 2023 год.

См. также

• Вычислительная электромагнетика
• Метод граничных элементов
• Быстрый мультипольный метод
• Вычислительная нейробиология
• Транскраниальная магнитная стимуляция
• Транскраниальная стимуляция постоянным током
• Электроэнцефалография
• Магнитоэнцефалография

Внешние ссылки

• Обзор интегральных уравнений для биоэлектрического моделирования , препринт .
• Институт Флэтайрон — сайт проекта FMM3D на GitHub Фонда Саймонса.