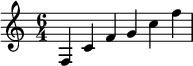Пифагорейские молотки

По легенде, Пифагор открыл основы музыкальной настройки , слушая звуки четырех кузневых молотов, которые производили созвучие и диссонанс при одновременном ударе . Согласно Никомаху II века н. э. в его гармониках Энхиридиона , [1] Пифагор заметил, что молоток А производит созвучие с молотком Б, когда их ударяют вместе, а молот С производит созвучие с молотком А, а молотки В и С производят диссонанс друг с другом. Молоток D производил такое идеальное созвучие с молоточком А, что казалось, что они «поют» одну и ту же ноту. Пифагор бросился в кузницу, чтобы выяснить, почему, и обнаружил, что объяснение кроется в соотношениях весов. Молоты весили 12, 9, 8 и 6 фунтов соответственно. Молоточки A и D находились в соотношении 2:1, что соответствует соотношению октав . Молоты B и C весили 8 и 9 фунтов. Их соотношения с молотком D были (12:8 = 3:2 = идеальная квинта ) и (12:9 = 4:3 = идеальная кварта ). Пространство между B и C представляет собой соотношение 9:8, что соответствует целому музыкальному тону или целому интервалу шага ( ).
| Молоток | Масса | Интервал | Долото | В С |
|---|---|---|---|---|
| А | 6 | С | ||
| Б | 8 | Г | ||
| С | 9 | Ф | ||
| Д | 12 | С' |
Легенда, по крайней мере в отношении молотов, явно ложна. Вероятно, это ближневосточная народная сказка. [2] Эти пропорции действительно имеют отношение к длине струны (например, монохорды ) — используя эти основные интервалы, можно построить хроматическую гамму и основную семитоновую диатоническую гамму, используемую в современной музыке, и Пифагор вполне мог оказать влияние на открытие этих пропорций (поэтому их иногда называют пифагорейской настройкой ) — но пропорции не имеют такого же отношения к весу молоточка и производимым ими звукам. [3] [4] Однако долота с молотковым приводом и равным поперечным сечением демонстрируют точную пропорцию между длиной или весом и собственной частотой . [5]
В более ранних источниках упоминается интерес Пифагора к гармонии и соотношению. Ксенократ (4 век до н.э.), хотя, насколько нам известно, не упоминал историю о кузнеце, описал интерес Пифагора в общих чертах: «Пифагор обнаружил также, что интервалы в музыке не возникают отдельно от числа; ибо они представляют собой взаимосвязь количества с количеством, поэтому он решил исследовать, при каких условиях возникают согласованные и несогласованные интервалы, а также все хорошо и плохо настроенное». [6] Какими бы ни были подробности открытия связи между музыкой и соотношением, ее считают [7] как исторически первое эмпирически надежное математическое описание физического факта. По существу, это символично и, возможно, ведет к пифагорейской концепции математики как способа действия природы . [8] Как Аристотель позже напишет , « пифагорейцы построили всю вселенную из чисел». [9] Микролог . Гвидо Ареццо повторяет легенду в главе XX [10]
- Размеры четырех молотов Пифагора.
Содержание легенды
[ редактировать ]По самой старой записанной версии [11] Согласно легенде, Пифагор, живший в VI веке до нашей эры, искал инструмент для измерения акустического восприятия, подобный тому, как геометрические величины измеряются с помощью циркуля или гири с помощью весов. Проходя мимо кузницы, где четыре (по более поздней версии, пять) мастеров работали молотками, он заметил, что каждый удар производит звуки разной высоты , что в паре приводит к гармонии. Он мог различать октаву , пятую и четвертую . Лишь одну пару, составлявшую интервал между четвертой и пятой (главную секунду ), он воспринимал как диссонансную . Взволнованный, он побежал в кузницу, чтобы проводить эксперименты. Там он обнаружил, что разница в высоте звука не зависит от формы молота, положения ударяемого железа или силы удара. Скорее, он мог связать высоту звука с весом молотков, который он точно измерял. Затем он вернулся домой, чтобы продолжить эксперименты.
Он повесил подряд четыре одинаково длинные, одинаково прочные и одинаково скрученные веревки на колышек, прикрепленный по диагонали к углу стены, придавая им разный вес, прикрепляя разные гири внизу. Затем он ударил по струнам попарно, и зазвучали те же гармонии, что и в кузнице. Струна с самой большой нагрузкой в двенадцать единиц в сочетании с наименее нагруженной струной, несущей шесть единиц, давала октаву. Таким образом, было очевидно, что октава основана на соотношении 12:6 или 2:1. Самая натянутая струна дала пятую часть со второй самой слабой струной (восемь единиц) и четвертую со второй по натяжению струной (девять единиц). Отсюда следовало, что пятый основывался на соотношении 12:8, или 3:2, а четвертый — на соотношении 12:9, или 4:3. Опять же, соотношение второй самой натянутой струны к самой слабой, 9:6, или 3:2, давало пятую часть, а соотношение второй самой натянутой струны к самой слабой, 8:6, или 4:3, давало четвертый. Для диссонансного интервала между пятой и четвертой выяснилось, что он основан на соотношении 9:8, что совпало с весовыми измерениями, проведенными в кузнице. Октава оказалась произведение пятого и четвертого:
Затем Пифагор распространил эксперимент на различные инструменты, экспериментировал с сосудами, флейтами, треугольниками , монохордой и т. д., всегда находя одни и те же числовые соотношения. Наконец, он представил широко используемую терминологию относительного звука.
Дальнейшие традиции
[ редактировать ]Говорят, что с изобретением монохорда для исследования и демонстрации гармонии пар струн с различным целочисленным соотношением длин Пифагор представил удобные средства иллюстрации обнаруженных им математических основ теории музыки. Монохорд, называемый κανών (kanōn) по-гречески и regula по-латыни, представляет собой резонирующую коробку с натянутой на нее струной. К коробке прилагается измерительная шкала. Устройство оснащено подвижным мостом, позволяющим разделить колеблющуюся длину струны; деление можно точно определить с помощью шкалы измерений. Это позволяет измерять интервалы. Несмотря на название «монохорд», что означает «однострунный», существовали и многострунные монохорды, способные воспроизводить однострунные интервалы. Однако неясно, когда был изобретен монохорд. Вальтер Буркерт относит это достижение ко времени после эпохи Аристотеля , который, по-видимому, не знал этого устройства; таким образом, он был введен спустя много времени после смерти Пифагора. [12] С другой стороны, Леонид Жмудь предполагает, что Пифагор, вероятно, проводил свой эксперимент, приведший к открытию числовых отношений, с помощью монохорды. [13]
Гиппас из Метапонта , ранний пифагорейец (конец VI — начало V веков до н.э.), проводил количественные исследования музыкальных интервалов. Эксперимент, приписываемый Гиппасу, с участием свободно колеблющихся круглых пластин разной толщины, физически корректен, в отличие от предполагаемых экспериментов Пифагора. Неясно, проводил ли соответствующие эксперименты Архит из Тарента , важный пифагорейец V/IV веков до нашей эры. Вероятно, он был скорее теоретиком, чем практиком в музыке, но ссылался на акустические наблюдения своих предшественников. Музыкальные примеры, которые он приводит в поддержку своей акустической теории, включают духовые инструменты; он не упоминает об экспериментах со струнными инструментами или отдельными струнами. Архит исходил из ошибочного предположения, что высота звука зависит от скорости распространения звука и силы удара по звукоиздающему телу; на самом деле скорость звука в данной среде постоянна, а сила влияет только на громкость. [14]
Интерпретация легенды
[ редактировать ]Вальтер Буркерт придерживается мнения, что, несмотря на свою физическую невозможность, легенду следует рассматривать не как произвольное изобретение, а, скорее, как имеющую значение, которое можно найти в греческой мифологии . Идейские дактилы , мифические изобретатели кузнечного дела, согласно мифу, были также изобретателями музыки. Таким образом, уже существовала очень древняя традиция, связывающая кузнечное дело с музыкой, в которой мифические кузнецы изображались обладателями секрета волшебной музыки. Буркерт видит в легенде о Пифагоре у кузнецов позднюю трансформацию и рационализацию древнего мифа о Дактиле: В легенде о Пифагоре кузнецы уже не предстают обладателями древних магических знаний, а, скорее, сами того не желая, становятся - хотя и незнающие – «учителя» Пифагора. [15]
В раннем средневековье называл Исидор Севильский библейского кузнеца Тубала изобретателем музыки; более поздние авторы последовали за ним в этом. Эта традиция еще раз демонстрирует идею связи кузнечного дела и музыки, которая также фигурирует в неевропейских мифах и легендах. [16] Тувал был сводным братом Джубала , считавшегося предком всех музыкантов. Оба были сыновьями Ламеха и, следовательно, внуками Каина . В некоторых христианских традициях Средневековья Юбал, наблюдавший за своим братом Тувалом, приравнивался к Пифагору. [17]
Другое объяснение предлагает Йорген Раастед вслед за Леонидом Жмудь. Гипотеза Раастеда гласит, что отправной точкой формирования легенды стал отчет об опытах Гиппаса. Гиппас использовал сосуды, называемые «сфаирами». Это слово было ошибочно перепутано со «сфирами» (молотами) из-за ошибки переписчика, и вместо имени Гиппаса в качестве автора экспериментов было использовано имя Пифагора. Отсюда и возникла легенда о кузнице. [18]
Основы теории музыки
[ редактировать ]Целые числа 6, 8, 9 и 12 по отношению к самому низкому тону (номер 12) соответствуют чистым интервалам четвертой (номер 9), квинты (номер 8) и октавы (номер 6) вверх:
| Целое число | Отношение к самое большое число 12 | Соотношение, уменьшенный | Номер соотношения | Обозначение интервала |
|---|---|---|---|---|
| 12 | 12:12 | 1:1 | 1.000 | Основной |
| 9 | 9:12 | 3:4 | 0.750 | Четвертый |
| 8 | 8:12 | 2:3 | 0.667 | Пятый |
| 6 | 6:12 | 1:2 | 0.500 | Октава |
Такие чистые интервалы воспринимаются человеческим ухом как безударные , так как громкость тонов не меняется. В нотах эти четыре пифагорейских тона могут быть выражены, например, мелодической последовательностью c’ – f’ – g’ – c»:
Если рассматривать эту последовательность тонов не от самого нижнего, а от самого высокого тона (цифра 6), то также получаются следующие интервалы: кварта (цифра 8), квинта (цифра 9) и октава (цифра 12) — в данном случае, однако, в сторону уменьшения:
| Целое число | Отношение к самое маленькое число 6 | Соотношение, уменьшенный | Номер соотношения | Обозначение интервала |
|---|---|---|---|---|
| 6 | 6:6 | 1:1 | 1.000 | Основной |
| 8 | 8:6 | 4:3 | 1.333 | Четвертый |
| 9 | 9:6 | 3:2 | 1.500 | Пятый |
| 12 | 12:6 | 2:1 | 2.000 | Октава |
Квинта и октава появляются по отношению к основному тону в естественном гармоническом ряду , но не к четвертому или его октавному эквиваленту . Этот интервал в кварту встречается в безвентиляционных духовых инструментах известных с древних времен и в гармонических обертонах струнных инструментов.
Значение для дальнейшего развития тональных систем.
[ редактировать ]Дальнейшее исследование интервалов, состоящих из октав, квинт и четверт, а также их кратных, в конечном итоге привело от диатонических гамм с семью различными тонами ( гептатоническая гамма ) в пифагорейской настройке к хроматической гамме с двенадцатью тонами. Волчьи интервалы в пифагорейской настройке создавали проблему: вместо чистых квинт A♭-E♭ и D♭-A♭ звучали квинты G♯-E♭ и C♯-A♭, расстроенные пифагорейской запятой . .
С появлением во второй половине XV века полифонии, помимо октавы и квинты, решающую роль в мажорных и минорных трезвучиях стала чистая терция. Хотя эту настройку невозможно было реализовать на двенадцатинотной клавиатуре, ее вполне можно было достичь в средней темперации. Его недостатком было то, что не на всех клавишах квинтового круга можно было играть. Чтобы исправить этот недостаток, были введены темперированные настройки, хотя и с тем компромиссом, что чистая треть в некоторых тональностях звучала более резко. В настоящее время большинство инструментов настраиваются одинаково темперно с помощью 12 клавиш, так что октавы звучат идеально чисто, квинты почти чисты, а терции звучат грубо.
Четыре пифагорейских тона в музыке.
[ редактировать ]В музыке четыре гармонических пифагорейских тона играют заметную роль в пентатонической гамме, особенно в первой, четвертой, пятой и восьмой ступенях диатонических гамм (особенно в мажоре и миноре), а также в составе каденций как основных тонов тоники. , субдоминантный и доминантный. Эта последовательность тонов часто появляется в каденциях с соответствующими аккордами:

Четыре пифагорейских тона присутствуют во многих композициях. Первые тона средневековых антифонов «Ad te levavi» и «Factus est repente» состоят по существу из четырех пифагорейских тонов, за исключением некоторых орнаментов и высоких нот. [19]
Другой пример — начало Пассакальи до минор Иоганна Себастьяна Баха. Тема состоит из пятнадцати тонов, из которых всего десять тонов и особенно последние четыре тона являются производными от последовательности.
Опровержение
[ редактировать ]Абсолютный шаг молотков
Резонансная частота стальных молотков, которые можно перемещать руками человека, обычно находится в ультразвуковом диапазоне и поэтому неслышна. Пифагор не мог воспринимать эти звуки, особенно когда разница в высоте звука молоточков составляла одну октаву.
Шаг в зависимости от веса молота
Частота колебаний свободно колеблющегося твердого тела, например продольной волны, обычно не пропорциональна его весу или объему, а пропорциональна его длине, которая изменяется при подобной геометрии только с кубическим корнем из объема.
Для молотов Пифагора для аналогичной геометрии применяются следующие числа передаточных чисел (значения в произвольных единицах измерения):
| Масса / Объем | Отношение к самый большой молоток | Длина головки молотка / Частота вибрации | Отношение к самый большой молоток | |
|---|---|---|---|---|
| 12 | 1.000 | 2.289 | 1.000 | |
| 9 | 0.750 | 2.080 | 0.909 | |
| 8 | 0.667 | 2.000 | 0.874 | |
| 6 | 0.500 | 1.817 | 0.794 |
Высота звука в зависимости от натяжения струны
Предположение о том, что частота колебаний струны пропорциональна натяжению, неверно. Скорее, частота вибрации пропорциональна квадратному корню из напряжения. Чтобы удвоить частоту вибрации, необходимо приложить в четыре раза большее натяжение и, таким образом, на веревку нужно повесить гирю, в четыре раза тяжелее.
Физические соображения
[ редактировать ]Созвучие
[ редактировать ]Целочисленные отношения частот
[ редактировать ]| Полная система частот | н | Частота ударов |
|---|---|---|
| 2:1 | 2 | |
| 3:1 | 3 | |
| 4:1 | 4 | |
| 5:1 | 5 |
Тот факт, что тон с основной частотой созвучен второму тону с целым кратным (с и ) этой основной частоты сразу видно из того, что максимумы и минимумы тональных колебаний синхронны во времени, но можно объяснить и следующим образом:
Частота ударов из двух одновременно звучащих тонов математически рассчитывается по разнице частот этих двух тонов и может быть услышан как комбинированный тон:
(см. Математическое описание ритма ).
Эта разница сама по себе находится в целочисленном отношении к основной частоте. :
Для всех целых кратных основной частоты второго тона существуют также целые кратные частоты ударов (см. таблицу справа), так что все тона звучат согласно.
Рациональные соотношения частот
[ редактировать ]| Рациональное соотношение частот | н | Частота ударов | Основная частота |
|---|---|---|---|
| 2:1 | 1 | ||
| 3:2 | 2 | ||
| 4:3 | 3 | ||
| 5:4 | 4 |
Даже для двух тонов, частоты которых находятся в рациональном соотношении к , есть созвучие. Частота второго тона определяется:
Следовательно, частота биений двух одновременно звучащих тонов определяется выражением:
При этом условии основная частота всегда является целым кратным частоте биений (см. таблицу справа). Поэтому никакого диссонанса не возникает.
Продольные колебания и собственная частота твердых тел.
[ редактировать ]Для оценки металлического блока рассмотрим однородную прямоугольную призму максимальной длины и изготовлен из материала, обладающего скоростью звука . Для режима вибрации по самой длинной стороне ( продольное колебание ) он имеет наименьшую собственную частоту. с пучностями на обоих концах и узлом посередине. [20]
.
Следовательно, шаг призмы не зависит от массы и площади поперечного сечения призмы, а площадь поперечного сечения может даже варьироваться. Причем сила и скорость при ударе по телу также не играют роли. По крайней мере, этот факт соответствует наблюдению, приписываемому Пифагору, о том, что воспринимаемая высота звука не зависела от рук (а значит, и сил) мастеров.
Тела с более сложной геометрией , такие как колокола , чашки или чаши , которые могут быть даже наполнены жидкостью, имеют собственные частоты, которые требуют значительно более сложных физических описаний, поскольку необходимо определить не только форму, но и толщину стенок или даже место удара. обдуманный. В этих случаях поперечные колебания также могут возбуждаться и слышны .
Молотки
[ редактировать ]
Очень большая кувалда (скорость звука в стали примерно = 5000 метров в секунду) с длиной головки молота = 0,2 метра имеет собственную частоту 12,5 килогерц. При площади поперечного сечения 0,1 квадратного метра (0,1 метра на 0,1 метра) он будет иметь необычно большую массу - почти 16 килограммов при плотности 7,86 грамма на кубический сантиметр. Частоты выше примерно 15 килогерц многие люди больше не воспринимают (см. слуховой порог ); поэтому собственная частота такого большого молотка почти не слышна. Молоточки с более короткими головками имеют еще более высокие собственные частоты, поэтому их невозможно услышать.
Наковальни
[ редактировать ]Большая стальная наковальня длиной = 0,5 метра имеет собственную частоту всего 5 килогерц и поэтому легко слышен.
Существуют разнообразные композиции , в которых композитор указывает использование наковальни в качестве музыкальных инструментов. Особенно известны две оперы из музыкальной драмы Кольцо Нибелунгов» « Рихарда Вагнера :
- «Золото Рейна» , Сцена 3, 18 наковальнь фа фа в трёх октавах
- Зигфрид , Акт 1, Кузнечная песня Зигфрида Nothung! Ничего! Завистливый меч!
Материалы с более низкой скоростью звука, чем сталь, такие как гранит или латунь , производят еще более низкие частоты с конгруэнтной геометрией. В любом случае в ранних рассказах наковальни не упоминаются, а в более поздних версиях легенды слышимые звуки наковальни приписываются молотам.
Металлические стержни
[ редактировать ]

Звуковые примеры долот с частотами вибрации, находящимися в целочисленных отношениях друг к другу:
Можно сравнить металлические стержни , такие как долота, используемые каменщиками, или раскалывающиеся клинья для разрушения камня, чтобы прийти к наблюдению, аналогичному тому, которое приписывалось Пифагору, а именно, что частота вибрации инструментов пропорциональна их весу . Если все металлические стержни, без учета сужающихся режущих кромок, имеют одинаковую площадь поперечного сечения A, но разную длину l , то их вес пропорционален длине и, следовательно, частоте вибрации, при условии, что металлические стержни возбуждаются продольные колебания ударами по продольной оси (примеры звука можно найти в рамке справа). [21]
Для изгибных осцилляторов , таких как камертоны или пластинки металлофонов , действуют другие условия и законы; следовательно, эти соображения к ним не применимы.
Колебания струн
[ редактировать ]
Струны можно закрепить на двух концах, каждый на перемычке . В отличие от твердого тела с продольными колебаниями, два моста устанавливают граничные условия для двух узловых точек вибрации; следовательно, колебательный узел расположен посередине.
Собственная частота и, следовательно, высота струн длиной не пропорциональны напряжению , а квадратному корню из напряжения. Более того, частота увеличивается с увеличением растягивающего усилия и, следовательно, с увеличением натяжения, а не уменьшается: [22]
Тем не менее частота колебаний обратно пропорциональна длине струны при постоянном натяжении, что можно непосредственно продемонстрировать на примере монохорда , якобы изобретенного Пифагором.
Прием
[ редактировать ]
Античность
[ редактировать ]Самое раннее упоминание об открытии Пифагором математической основы музыкальных интервалов встречается у платоника Ксенократа (4 век до н. э.); поскольку это всего лишь цитата из утерянного труда этого мыслителя, неясно, знал ли он легенду о кузне. [23] В IV веке до нашей эры уже высказывалась критика пифагорейской теории интервалов, хотя и без ссылки на легенду о Пифагоре; философ и теоретик музыки Аристоксен считал это ложным.

Самая старая зарегистрированная версия легенды была представлена спустя столетия после Пифагора неопифагорейцем Никомахом из Герасы , который в I или II веке нашей эры задокументировал эту историю в своем Harmonikḗ Encheirídion («Справочник гармонии»). Он опирался на философа Филолая , пифагорейца V века до нашей эры, для представления числовых соотношений в теории музыки. [24]
Знаменитый математик и теоретик музыки Птолемей (II век нашей эры) знал о весовом методе, передаваемом легендой, но отверг его. Однако он не признавал ложности весовых опытов; он лишь критиковал их неточности по сравнению с точными измерениями на монохорде. [25] Вполне вероятно, что свои знания о легендарной традиции он получил не от Никомаха, а из более древнего источника, ныне утерянного. [26]
Хронологически трудно определить место теоретика музыки императорской эпохи Гауденция описал легенду в своем Harmonikḗ Eisagōgḗ («Введение в гармонию»), в версии, немного короче, чем версия Никомаха. Философ неоплатоник - Ямвлих Халкидский , работавший учителем философии в конце III — начале IV веков, написал биографию Пифагора под названием « О пифагорейской жизни» , в которой воспроизвел кузнечную легенду в версии Никомаха.
В первой половине V века писатель Макробий широко обсуждал легенду о кузнеце в своем комментарии к Цицерона « Somnium Scipionis» , который он описал аналогично Никомаху. [27]

Самый сильный резонанс среди теоретиков античной музыки, поднявшихся этому повествованию, был достигнут Боэцием с его учебником De Institutione Musica («Введение в музыку»), написанным в начале VI века, в котором он первоначально описывает попытки Пифагора понять музыку в ковать, а потом дома. [28] Неясно, полагался ли он на рассказ Никомаха или на другой источник. В отличие от всей более ранней традиции, он сообщает о пяти молотах вместо четырех, как предполагали более ранние авторы. Он утверждает, что Пифагор отверг пятый молот, потому что он приводил к диссонансу со всеми остальными молотами. Согласно рассказу Боэция (как и Макробия), Пифагор проверил свое первоначальное предположение о том, что разница в звуке возникла из-за разной силы рук мужчин, заставив кузнецов поменяться молотками, что привело к его опровержению. Что касается экспериментов в доме Пифагора, Боэций пишет, что философ сначала подвешивал в кузнице веревки с весом, равным весу молотков, а затем экспериментировал с трубками и чашками, причем все эксперименты давали те же результаты, что и первоначальные с молотками. . Опираясь на легенду, Боэций обращается к вопросу достоверности чувственных восприятий с точки зрения науки и теории познания. Решающим моментом является то, что Пифагор изначально был побужден чувственным восприятием к формулированию своего вопроса и гипотез, и посредством эмпирической проверки гипотез он пришел к неопровержимой уверенности. Путь к познанию шел от чувственного восприятия к исходной гипотезе, оказавшейся ошибочной, затем к формированию правильного мнения и, наконец, к его проверке. Боэций признает необходимость и ценность чувственного восприятия и формирования мнений на пути к пониманию, хотя и в качестве Платоник , он по своей сути скептически относится к чувственному восприятию из-за его склонности к ошибкам. Подлинное знание, по его мнению, возникает лишь тогда, когда уловлена закономерность, позволяющая исследователю освободиться от первоначальной зависимости от ненадежного чувственного восприятия. Суждение исследователя не должно основываться исключительно на чувственном суждении, полученном на основе эмпирического опыта, а, скорее, должно быть вынесено только после того, как он путем размышлений нашел правило, которое позволяет ему позиционировать себя за пределами возможного сенсорного обмана. [29]
В VI веке ученый Кассиодор писал в своих «Институциях» , что Гауденций приписывал начало «музыки» Пифагору в своем рассказе о легенде о кузнеце. Он имел в виду теорию музыки, как и Ямвлих, который, ссылаясь на рассказ о кузнеце и описанные там эксперименты, называл Пифагора изобретателем «музыки». [30]
Средний возраст
[ редактировать ]В раннем средневековье Исидор Севильский упомянул легенду о кузнеце в своих «Этимологиях» , ставших фундаментальным справочником для образованных в Средние века. Он кратко упомянул легенду, заимствовав формулировку Кассиодора, а также назвав Пифагора изобретателем музыки. [31] Поскольку Кассиодор и Исидор были крупнейшими авторитетами в Средние века, распространилось мнение, что Пифагор открыл фундаментальный закон музыки и, таким образом, был ее основателем. Несмотря на столь радикальные заявления, средневековые теоретики музыки предполагали, что музыка существовала до Пифагора и что «изобретение музыки» относится к открытию ее принципов. [32]
В 9 веке музыковед Аврелиан Реоме рассказал эту легенду в своей «Musica disciplina» («Теория музыки»). За рассказом Аврелиана в X веке последовал Регино Прюмский в своей работе De Harmonica Institutione («Введение в гармоническую теорию»). Оба подчеркивали, что Пифагору была предоставлена возможность сделать свое открытие в кузнице по божественному провидению. [33] В древности Никомах и Ямвлих уже говорили о демоническом провидении, а Боэций превратил это в божественный указ.
В 11 веке легендарный материал обрабатывался в Carmina Cantabrigiensia . [34]

В первой половине XI века Гвидо Ареццо , самый известный теоретик музыки средневековья, изложил легенду о кузнеце в заключительной главе своего «Микролога» , взяв за основу версию Боэция, которого он назвал конкретно. Гвидо заметил вначале: Никто бы никогда не открыл ничего определенного в этом искусстве (музыке) , если бы в конце концов божественная доброта не вызвала по своему велению следующее событие. Тот факт, что молоточки весили 12, 9, 8 и 6 единиц и таким образом издавали гармоничный звук, он объяснял промыслом Божьим. [35] Он также упомянул, что Пифагор, начиная со своего открытия, изобрел монохорд, но не вдавался в подробности о его свойствах.
Работа «De musica» Йоханнеса Котто (также известного как Джон Коттон или Йоханнес Аффлигеменсис) была проиллюстрирована сценой кузнеца около 1250 года анонимным книжным иллюминатором в цистерцианском аббатстве Альдерсбах . [36]
Среди теоретиков средневековой музыки, рассказавших легенду о кузнице по версии Боэция, были также Хуан Хиль де Самора (Иоганнес Эгидиус фон Самора), действовавший в конце 13 - начале 14 веков, Иоганнес де Мюрис и Симон Тунстеде в 14 веке. века, и Адам фон Фульда на пороге раннего Нового времени в 15 веке.
Как противник пифагорейской концепции, согласно которой созвучия основаны на определенных числовых соотношениях, Иоганн де Грошейо появился в 13 веке, начиная с аристотелевской точки зрения. Хотя он прямо заявил, что Пифагор открыл принципы музыки, и рассказал легенду о кузнице, цитируя Боэция, которого считал заслуживающим доверия, он отверг пифагорейскую теорию созвучия, которую хотел свести к просто метафорическому выражению. [37]
Ранний современный период
[ редактировать ]

Франчино Гаффурио опубликовал в Неаполе в 1480 году свою работу Theoricum opus musice science («Теоретическая теория музыки»), которая была переработана и переиздана в 1492 году под названием Theorica musice («Теория музыки»). В нем он представил версию легенды о кузнице, превзошедшую в деталях все предыдущие рассказы. Он основал свою версию на версии Боэция и добавил шестой молот, чтобы включить в повествование как можно больше тонов октавы. В четырех графических изображениях он представил музыкальные инструменты или генераторы звука, каждый из которых имел шесть гармонических тонов, и указал на этикетках цифры 4, 6, 8, 9, 12 и 16, соответствующие тонам. В дополнение к четырем традиционным пропорциям легенды (6, 8, 9 и 12) он добавил 4 и 16, которые представляют собой тон на квинту ниже и еще один тон на кварту выше. Вся последовательность тонов теперь простирается не только на одну, но и на две октавы. Эти числа соответствуют, например, тонам f – c’ – f’ – g’ – c» – f»:
Художнику Эрхарду Сансдорферу в 1546 году было поручено создать фреску в гессенском замке Бюдинген , которая хорошо сохранилась и представляет историю музыки, начиная с кузницы Пифагора, как компендиум. [38]
Джозеффо Зарлино также рассказал эту легенду в своей работе Le istitutioni Harmoniche («Основы гармонии»), которую он опубликовал в 1558 году; как и Гаффурио, он основывал свое повествование на версии Боэция. [39]
Теоретик музыки Винченцо Галилей, отец Галилео Галилея, опубликовал в 1589 году свой трактат Discorso intorno all'opere dimesser Джозеффо Зарлино («Рассуждение о произведениях господина Джозеффо Зарлино»), направленный против взглядов его учителя Зарлино. . В нем он указывал, что сведения в легенде о нагружении струн гирями неточны.[1]

В 1626 году в «Thesaurus philopoliticus» Даниэля Мейснера была гравюра на меди Эберхарда Кизера под названием «Дуйнкирхен», на которой были изображены только три кузнеца на наковальне. Подпись на латыни и немецком языке гласит:[2]
- Когда по нему ударяют три раза, он звучит как различные удары.
- Музыка Пифагора закладывает здесь основы принципа(эпса).
- Наковальня издает тройные удары, производя три разных тона.
- Музыка — это фундамент, построенный Пифагором, которого не могла бы достичь ни одна ослиная голова.
Спустя несколько лет дело окончательно прояснилось после того, как Галилео Галилей и Марин Мерсенн открыли законы колебаний струн. В 1636 году Мерсенн опубликовал свою «Всемирную гармонию», в которой объяснил физическую ошибку легенды: частота вибрации пропорциональна не напряжению, а его квадратному корню.[3]
Некоторые композиторы включили эту тему в свои произведения, в том числе Георг Мюффа в конце 17 века. [40] и Руперт Игнац Майр . [41]
современная эпоха
[ редактировать ]Еще в XIX веке Гегель в своих лекциях по истории философии предполагал физическую точность предполагаемых измерений, упомянутых в легенде о Пифагоре. [42]
Вернер Гейзенберг подчеркнул в эссе, впервые опубликованном в 1937 году, что пифагорейское «открытие математической определенности гармонии» основано на «идее значимой силы математических структур», «фундаментальной идее, которую современная точная наука унаследовала от древности». ; открытие, приписываемое Пифагору, принадлежит «к сильнейшим порывам человеческой науки вообще». [43]
Совсем недавно были опубликованы отчеты, в которых легенда воспроизводится некритически, без ссылки на ее физическую и историческую ложность. [44] Например, в научно-популярной книге «Пятый молот: Пифагор и дисгармония мира» Дэниела Хеллера-Роазена . [45]
Источники
[ редактировать ]- Готфрид Фридлейн (Hrsg.): Аниций Манлий Торкват Северин Боэций по инструкции по второй книге арифметики, по инструкции по пятой книге по музыке. Минерва, Франкфурт-на-Майне, 1966 (Nachdruck der Ausgabe Leipzig 1867, онлайн ; deutsche Übersetzung онлайн )
- Михаэль Гермесдорф (переводчик): Micrologus Guidonis de disciplina artis musicae, краткий трактат Гвидо о правилах музыкального искусства . Трир 1876 г. ( онлайн )
- Ильде Иллюминаты, Фабио Беллиссима (Hrsg.): Франкино Гаффурио: Theorica musice. Galluzzo Editions, Флоренция, 2005 г., ISBN 88-8450-161-X , стр. 66–71 (латинский текст и итальянский перевод)
Дальнейшее чтение
[ редактировать ]- Уолтер Буркерт: Мудрость и наука. Исследования Пифагора, Филолая и Платона (= вклад Эрлангера в лингвистику и искусство . Том 10). Ганс Карл, Нюрнберг, 1962 г.
- Аня Хайльманн: Теория музыки Боэция и квадривиум. Введение в неоплатоническую подоплеку «De Institutione Musica» . Ванденхук и Рупрехт, Геттинген, 2007 г., ISBN 978-3-525-25268-0 , S. 203–222 ( [1] в Google Книгах )
- Вернер Кейл (ред.): Основные тексты по музыкальной эстетике и теории музыки. Вильгельм Финк, Падерборн, 2007 г., ISBN 978-3-8252-8359-9 , S. 342–346 ( [2] в Google Книгах )
- Барбара Мюнксельхаус: Музыкальный Пифагор. О рецепции пифагорейской теории музыки как четырехмерной науки в латинском средневековье (= серия сочинений Орфея по основным вопросам музыки . Том 19). Издательство систематического музыковедения, Бонн – Бад-Годесберг, 1976 г.
- Йорген Раастед: Забытая версия анекдота об эксперименте Пифагора с молотком. В: Cahiers de l'Institut du Moyen-Âge grec et latin . Полоса 31а, 1979, С. 1–9.
- Леонид Жмудь: Наука, философия и религия в раннем пифагореизме. Академия Верлаг, Берлин, 1997 г., ISBN 3-05-003090-9
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Вайс, Пьеро и Ричард Тарускин, ред. Музыка в западном мире: история в документах . 2-е изд. Np: Томсон Ширмер, 1984. 3. ISBN 9780534585990 .
- ^ Кеннет Сильван Гатри, Дэвид Р. Фиделер (1987). Справочник и библиотека по Пифагору: Антология древних сочинений, относящихся к Пифагору и пифагорейской философии , стр.24. Красное Колесо/Вайзер. ISBN 9780933999510 .
- ^ Кристенсен, Томас, изд. Кембриджская история теории западной музыки . Кембридж: Издательство Кембриджского университета, 2002. 143. ISBN 9780521623711 .
- ^ Буркерт, Уолтер (1972). Знание и наука в древнем пифагореизме , стр.375. ISBN 9780674539181 . Цитируется по Кристенсену, 2002 г., стр. 143.
- ^ Маркус Бауч: О пифагорейских корнях григорианских ладов , английский: О пифагорейских корнях григорианских ладов , Mater Dolorosa (Берлин-Ланквиц) , март 2012 г., получено 31 августа 2017 г.
- ^ Баркер (2004). Эндрю (ред.). Греческие музыкальные сочинения (1-е изд.). Кембридж: Издательство Кембриджского университета . п. 30. ISBN 978-0-521-61697-3 .
- ^ Лукас Н. Х. Бунт; Филип С. Джонс; Джек Д. Бедьен (1988). Исторические корни элементарной математики (Переиздание). Нью-Йорк: Dover Publications . п. 72. ИСБН 978-0-486-25563-7 .
- ^ Кристиан, Джеймс (26 января 2011 г.). Философия. Введение в искусство удивляться . Wadsworth Pub Co. p. 517. ИСБН 978-1-111-29808-1 .
- ^ Уотерфилд, пер. с комментариями Робина (2000). Первые философы: досократики и софисты (1. опубликовано под изд. Оксфордской мировой классики в мягкой обложке). Оксфорд: Оксфордский университет. Нажимать. п. 103 . ISBN 978-0-19-282454-7 .
пифагорейцы построили всю вселенную из чисел.
- ^ "GUIMICB_MBBR2784" . chmtl.indiana.edu Проверено 9 мая 2023 г.
Это были древние, неопределенные инструменты. и толпа певцов была слепа. Ибо нет разницы между именами человеческими. и ему удалось собрать описание симфонии с некоторыми аргументами. и он никогда не мог знать ничего определенного об этом искусстве. если только божественная милость своим кивком не устроит, наконец, то, что последует. Некий великий философ путешествовал вместе с Пифагором. пришел на завод. в котором они ударили пятью молотами по одной наковальне. Философ подошел к ним, удивляясь их нежному согласию. и сначала надеясь на разнообразие рук [ф.20р], что звук и модуляция существуют. Он поменял молотки. Таким образом она следовала за каждым из них по-своему. Поэтому я убрал тот, который расходился с остальными. Он взвешивал других. И чудесным образом, с божественным кивком, первый .12 второй VIII. третий .VIII. четвертый .VI. Я не знаю, на каких гирях их взвешивали. Поэтому он изучил музыкальную науку в пропорциях и составе чисел. Ибо эта конституция состояла из четырех молотов. который состоит только из четырех букв .ADEa. Наконец, если A имеет .XII. и Д 81 и пусть кватернеры идут в ногу. будет иметь .А. в .XII. тройной .III. и Д. в .VIII. тройной .III. Вот диатессарон. Опять же, поскольку у него А .XII. если он имеет E. VIII. кватернер будет иметь три ступени .A. действительно два Э. и ясно, что диапенте. Пусть снова .12 в А. и .6 другому а. Сенарий — полдюжины. точно так же, как оно собрано из острой половины другого А. Итак, есть камертон. С тех пор она .а. к Д. диатессарону к е диапенте с другой стороны, он воспроизводится камертоном. D также к электронному тону. обоим А - диатессарон и это звучит ясно. И Е также диктует Д. тон как для Аа диапенте, так и для диатессарона. очень диез с диапазоном ля. с D диапанте. когда Е звучит диатессарон. которые любопытный следователь нашел в вышеупомянутых числах. Ибо начиная с этого момента Боэций был пропагандистом этого искусства. Он показал много чудесной и сложной гармонии этого искусства с пропорциями чисел. [ф.20в] Что еще? Упорядочение голосов по вышеупомянутым видам. Пифагор был первым, кто составил монохорд из четырех струн. в котором нет похотливости. но внимательно открывайте информацию ст. Это нравилось всем мудрецам. и до сегодняшнего дня искусство постепенно росло и процветало. тем же учителем, всегда освещающим человеческую тьму. чья высшая мудрость пронизывает все века.
- ^ Никомах фон Гераса, Справочник по гармоникам 6, перевод Ани Хейльманн: Музыкальная теория Боэция и квадривиум , Геттинген, 2007, стр. 345–347, буквально цитируется в Ямблихосе фон Халкиде, О пифагорейской жизни 115–121, перевод Михаэля фон Альбрехт: Ямвлих. Пифагор: Легенда – Доктрина – Образ жизни , Дармштадт, 2002, стр. 109–113.
- ^ Вальтер Буркерт: Мудрость и наука , Нюрнберг, 1962, с. 353 и примечание 28.
- ^ Леонид Жмудь: Наука, философия и религия в раннем пифагореизме , Берлин, 1997, стр. 193–196; см. также Барбара Мюнксельхаус: Pythagoras musicus , Бонн – Бад-Годесберг, 1976, стр. 28 f.
- ^ Вальтер Буркерт: Мудрость и наука , Нюрнберг, 1962, стр. 362–364; Леонид Жмудь: Наука, философия и религия в раннем пифагореизме , Берлин, 1997, стр. 196–199. Скептицизм относительно акустических экспериментов Архитаса выражен Карлом А. Хаффманом : Archytas of Tarentum , Cambridge, 2005, стр. 129–148; см. также стр. 473–475. Он указывает, что Архит в основном опирается на сведения своих предшественников и житейский опыт.
- ^ Вальтер Буркерт: Мудрость и наука , Нюрнберг, 1962, с. 355.
- ^ Вальтер Буркерт: Мудрость и наука , Нюрнберг, 1962, с. 355; Барбара Мюнксельхаус: Pythagoras musicus , Бонн – Бад-Годесберг, 1976, стр. 38 f., 46.
- ^ Джеймс В. Маккиннон: Джубал и Пифагор, кто изобретатель музыки? В: The Musical Quarterly , vol. 64, нет. 1, 1978, с. 1–28; Пол Э. Байхнер: средневековый представитель музыки, Джубал или Тубалкаин? (= Тексты и исследования по истории средневекового образования 2), Нотр-Дам, Индиана, 1954; Фрэнсис Оливье Циммерманн: Кузнечное дело и гармония. От Пифагора до Тувалкаина и Иувала. В: Циммерманн: Орфей: живое искусство, искусство речи и мелодии ( онлайн ).
- ^ Йорген Раастед: «Забытая версия анекдота об эксперименте Пифагора с молотком». В: Cahiers de l'Institut du Moyen-Âge grec et latin 31a, 1979, стр. 1–9, здесь: 6 сл.; Леонид Жмудь: «Wissenschaft, Philosophie und Religion im frühen Pythagoreismus», Берлин, 1997, с. 192. (Перевод с немецкого)
- ^ См. Factus est repente , Отношения слова и мелодии в григорианском пении; Первая песнь церковного года .
- ^ Людвиг Бергманн, Клеменс Шефер: Учебник экспериментальной физики. Том 1, 9-е издание. Берлин 1974, Глава 83: Звуковые передатчики , раздел Продольные колебания .
- ^ Маркус Бауч: О пифагорейских корнях григорианских ладов ( онлайн ).
- ^ Людвиг Бергманн, Клеменс Шефер: Учебник экспериментальной физики. Том 1, 9-е издание. Берлин 1974, Глава 83: Звукопередатчик , раздел Saite .
- ^ Ксенократ Фрагмент 9 H. См. Вальтер Буркерт: Мудрость и наука , Нюрнберг, 1962, с. 57 и Леонид Жмудь: Наука, философия и религия в раннем пифагореизме , Берлин, 1997, с. 193.
- ^ Этот отрывок из работы Никомаха отредактирован, переведен на английский язык и прокомментирован Карлом А. Хаффманом: Филолай Кротонский , Кембридж, 1993, стр. 145–165.
- ^ Барбара Мюнксельхаус: Pythagoras musicus , Бонн – Бад-Годесберг, 1976, с. 52.
- ^ Вальтер Буркерт: Мудрость и наука , Нюрнберг, 1962, с. 355.
- ^ Макробий, Комментарии к сну Сципиона 2,1,8–13.
- ^ Боэций, De Institutione Musica 1.10–11, перевод Ани Хейльманн: Теория музыки Боэция и квадривиум , Геттинген, 2007, стр. 342–345.
- ^ Научную и эпистемологическую основу см. Аня Хейльманн: Теория музыки Боэция и квадривиум , Геттинген, 2007, стр. 205–218.
- ^ Кассиодор, Institutiones 2,5,1; ср. Ямвлих, De vita Пифагор 121
- ^ Исидор, Этимологии 3,16,1.
- ^ Барбара Мюнксельхаус: Pythagoras musicus , Бонн – Бад-Годесберг, 1976, стр. 15–17.
- ^ Ганс Мартин Клинкенберг : Упадок квадривиума в раннем средневековье. В: Йозеф Кох (редактор): Artes liberes. От древнего образования к науке Средневековья , Лейден, 1976, стр. 1–32, здесь: 24 f.
- ^ Carmina Cantabrigiensia , Песня 45 и последовательность Пифагора (первая половина XI века); см. Вальтер Кранц: Пифагор в Carmina Cantabrigiensia ( онлайн ; PDF; 2,3 МБ).
- ^ Гвидо из Ареццо, Micrologus 20 ( немецкий перевод онлайн ).
- ^ Рукопись из собрания Альдерсбаха, Clm 2599, л. 96v, Баварская государственная библиотека, Мюнхен
- ^ Барбара Мюнксельхаус: Pythagoras musicus , Бонн – Бад-Годесберг, 1976, с. 16, 76; Фрэнк Хентшель: Чувственность и разум в теории средневековой музыки , Штутгарт, 2000, стр. 148–150 ( онлайн ).
- ^ Уолтер Салмен : Музыкальная жизнь в 16 веке, Лейпциг, 1976; черно-белая фотография онлайн .
- ^ Вернер Кейл (редактор): Основные тексты по музыкальной эстетике и теории музыки , Падерборн, 2007, стр. 56 (перевод текста Зарлино).
- ^ Георг Мюффа: Nova Cyclopeias Harmonica (1690).
- ^ Руперт Игнац Майр: Пифагорейский Шмидс-Фюнкляйн (1692).
- ^ Вернер Кейл (редактор): Основные тексты по музыкальной эстетике и теории музыки , Падерборн, 2007, стр. 343.
- ^ Вернер Гейзенберг: Мысли древней натурфилософии в современной физике . В: Вернер Гейзенберг: Изменения в основах естествознания , 8-е издание, Штутгарт, 1949, стр. 47–53, здесь: 50.
- ^ Арнольд Кейзерлинг: История стилей мышления. 3. Логическое мышление ( онлайн ); Карл Шумередер: Музыка и математика ( онлайн ); Арнольд Кейзерлинг: Новое имя Бога. Формула мира и ее аналогии в реальности , Вена 2002, с. 71 ( Молоты Пифагора , стр. 71, в Google Books ).
- ^ Даниэль Хеллер-Роазен: Пятый молот: Пифагор и дисгармония мира , Франкфурт-на-Майне, 2014, стр. 14–22 ( онлайн ).