Список F 4 многогранников
 24-ячеечный |
В 4-мерной геометрии существует 9 однородных 4-многогранников с симметрией F 4 и одна киральная полусимметрия, курносая 24-ячейка . Существует одна самодвойственная правильная форма — 24-ячеечная с 24 вершинами.
Визуализация
[ редактировать ]Каждую из них можно визуализировать как симметричные орфографические проекции в плоскостях Кокстера группы F 4 Кокстера и других подгрупп.
Трехмерное изображение рисуется в виде проекций диаграммы Шлегеля с центром в ячейке поз. 3, с постоянной ориентацией, а 5 ячеек в положении 0 показаны сплошными.
| # | Имя Диаграмма Кокстера Символ Шлефли | График | Диаграмма Шлегеля | Сеть | |||||
|---|---|---|---|---|---|---|---|---|---|
| FF4 [12] | Б 4 [8] | BБ3 [6] | BБ2 [4] | Октаэдр центрированный | Двойной октаэдр центрированный | ||||
| 1 | 24-ячеечный (исправленный 16-ячеечный) {3,4,3} = г{3,3,4} |  |  |  |  |  |  |  | |
| 2 | выпрямленный 24-клеточный (сочлененный 16-клеточный) г{3,4,3} = рр{3,3,4} |  |  |  |  |  |  |  | |
| 3 | усеченный 24-клеточный (усеченный, 16-ячеечный) т{3,4,3} = тр{3,3,4} |  |  |  |  |  |  | 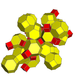 | |
| 4 | сочлененный 24-клеточный рр{3,4,3} |  |  |  |  |  |  |  | |
| 5 | усеченный, 24 ячейки тр{3,4,3} |  |  |  |  |  |  |  | |
| 6 | усеченный, 24-клеточный т 0,1,3 {3,4,3} |  |  |  |  |  |  |  | |
| # | Имя Диаграмма Кокстера Символ Шлефли | График | Диаграмма Шлегеля | Сеть | |||
|---|---|---|---|---|---|---|---|
| FF4 [[12]] = [24] | Б 4 [8] | BБ3 [6] | BБ2 [[4]] = [8] | Октаэдр центрированный | |||
| 7 | * сморщенный 24-клеточный т 0,3 {3,4,3} |  |  |  |  |  |  |
| 8 | * усеченные 24 ячейки 2т{3,4,3} |  |  |  |  |  |  |
| 9 | * всеусеченный 24-клеточный т 0,1,2,3 {3,4,3} |  |  |  |  |  |  |
| # | Имя Диаграмма Кокстера Символ Шлефли | График | Диаграмма Шлегеля | Ортогональный Проекция | Сеть | ||||
|---|---|---|---|---|---|---|---|---|---|
| FF4 [12] + | Б 4 [8] | BБ3 [6] + | BБ2 [4] | Октаэдр центрированный | Двойной октаэдр центрированный | Октаэдр центрированный | |||
| 10 | курносый 24-клеточный с{3,4,3} |  |  |  |  |  |  | 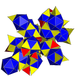 | |
| 11 Неоднородный | рунчик курносый, 24 ячейки с 3 {3,4,3} |  |  |  |  | ||||
Координаты
[ редактировать ]Координаты вершин для всех 15 форм приведены ниже, включая двойные конфигурации из двух обычных 24-ячеек. (Двойные конфигурации выделены жирным шрифтом.) Активные кольца в первом и втором узлах генерируют точки в первом столбце. Активные кольца в третьем и четвертом узлах генерируют точки во втором столбце. Сумма каждой из этих точек затем переставляется по позициям координат и комбинациям знаков. Это генерирует все координаты вершин. Длина ребра равна 2.
Единственным исключением является курносая 24-ячейка, которая генерируется за счет половины перестановок координат, а только четного числа перестановок координат. φ=( √ 5 +1)/2.
| # | Базовая точка(и) т(0,1) | Базовая точка(и) т(2,3) | Символ Шлефли | Имя | Диаграмма Кокстера |
|---|---|---|---|---|---|
| 1 | (0,0,1,1) √ 2 | {3,4,3} | 24-ячеечный | ||
| 2 | (0,1,1,2) √ 2 | г {3,4,3} | выпрямленный 24-клеточный | ||
| 3 | (0,1,2,3) √ 2 | т{3,4,3} | усеченный 24-клеточный | ||
| 10 | (0,1,φ,φ+1) √ 2 | с{3,4,3} | курносый 24-клеточный | ||
| 2 | (0,2,2,2) (1,1,1,3) | г {3,4,3} | выпрямленный 24-клеточный | ||
| 4 | (0,2,2,2) + (1,1,1,3) + | (0,0,1,1) √ 2 " | рр{3,4,3} | сочлененный 24-клеточный | |
| 8 | (0,2,2,2) + (1,1,1,3) + | (0,1,1,2) √ 2 " | 2т{3,4,3} | усеченный 24 ячейки | |
| 5 | (0,2,2,2) + (1,1,1,3) + | (0,1,2,3) √ 2 " | тр{3,4,3} | усеченный, 24 ячейки | |
| 1 | (0,0,0,2) (1,1,1,1) | {3,4,3} | 24-ячеечный | ||
| 7 | (0,0,0,2) + (1,1,1,1) + | (0,0,1,1) √ 2 " | т 0,3 {3,4,3} | сморщенный 24-клеточный | |
| 4 | (0,0,0,2) + (1,1,1,1) + | (0,1,1,2) √ 2 " | т 1,3 {3,4,3} | сочлененный 24-клеточный | |
| 6 | (0,0,0,2) + (1,1,1,1) + | (0,1,2,3) √ 2 " | т 0,1,3 {3,4,3} | усеченный, 24-клеточный | |
| 3 | (1,1,1,5) (1,3,3,3) (2,2,2,4) | т{3,4,3} | усеченный 24-клеточный | ||
| 6 | (1,1,1,5) + (1,3,3,3) + (2,2,2,4) + | (0,0,1,1) √ 2 " " | т 0,2,3 {3,4,3} | усеченный, 24-клеточный | |
| 5 | (1,1,1,5) + (1,3,3,3) + (2,2,2,4) + | (0,1,1,2) √ 2 " " | тр{3,4,3} | усеченный, 24 ячейки | |
| 9 | (1,1,1,5) + (1,3,3,3) + (2,2,2,4) + | (0,1,2,3) √ 2 " " | т 0,1,2,3 {3,4,3} | Всеусеченный 24-клеточный | |
Ссылки
[ редактировать ]- Дж. Х. Конвей и М. Дж. Т. Гай : Четырехмерные архимедовы многогранники , материалы коллоквиума по выпуклости в Копенгагене, стр. 38 и 39, 1965 г.
- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус , Симметрии вещей 2008, ISBN 978-1-56881-220-5 (глава 26)
- ХСМ Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 Wiley::Калейдоскопы: Избранные сочинения HSM Коксетера
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380–407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
Внешние ссылки
[ редактировать ]- Клитцинг, Ричард. «4D однородные 4-многогранники» .
- Однородные выпуклые многогранники в четырех измерениях: Марко Мёллер (на немецком языке)
- Мёллер, Марко (2004). Viersizede Archimedische Polytope (PDF) (Докторская диссертация) (на немецком языке). Университет Гамбурга.
- Однородные многогранники в четырех измерениях , Георгий Ольшевский.
- Выпуклая равномерная полихора на основе 24-клеточной , Георгия Ольшевского.