Эффект квантового зала

Эффект квантового зала (или квантового зала ) является версией эффекта , в двумерных электронных подвергших квантовой эффект , которая наблюдается зала _{целочисленного} системах квантованные значения

$R_{xy}={\frac {V_{\text{Hall}}}{I_{\text{channel}}}}={\frac {h}{e^{2}\nu }},$

Там, где v _Hall - это напряжение зала , I _-канал канала - ток , E - элементарный заряд , а H - постоянная Планка . Делитель ν может принять либо целое число ( ν = 1, 2, 3, ... ), либо дробное ( ν = ⁠ 1 / 3 ⁠ , ⁠ 2 / 5 ⁠ , ⁠ 3 / 7 ⁠ , ⁠ 2 / 3 ⁠ , ⁠ 3 / 5 ⁠ , ⁠ 1 / 5 ⁠ , ⁠ 2 / 9 ⁠ , ⁠ 3 / 13 ⁠ , ⁠ 5 / 2 ⁠ , ⁠ 12/5 . ⁠ ) , ... Значения Здесь ν примерно, но не совсем равна коэффициенту заполнения уровней Ландау . Эффект квантового зала называется целым числом или фракционным эффектом квантового зала в зависимости от того, является ли ν целым числом или фракцией, соответственно.

Поразительной особенностью эффекта целочисленного квантового зала является стойкость квантования (то есть плато Холла), поскольку электронная плотность варьируется. Поскольку электронная плотность остается постоянной, когда уровень Ферми находится в чистом спектральном зазоре, эта ситуация соответствует тому, где уровень Ферми является энергией с конечной плотностью состояний, хотя эти состояния локализованы (см. Локализацию Андерсона ).

Дробный эффект квантового зала является более сложным и все еще считается открытой проблемой исследования. Его существование в основном зависит от электрон -электронных взаимодействий. В 1988 году было предложено, что был квантовый эффект зала без уровней Ландау . Этот эффект квантового зала называется эффектом квантового аномального зала (QAH). Существует также новая концепция эффекта Quantum Spin Hall , которая является аналогом эффекта квантового зала, где спиновые токи текут вместо токов заряда.

Приложения

Стандарты электрического сопротивления

Квантование проводимости зала ( $G_{xy}=1/R_{xy}$) имеет важное свойство чрезвычайно точного. Было установлено, что фактические измерения проводимости зала являются целочисленными или дробными кратными ⁠ e ² / h ⁠ почти одной части в миллиарде. позволило определить новый практический стандарт для электрического сопротивления , основанный на квантовом сопротивлении, заданном постоянным r _K. Это Это названо в честь Клауса фон Клицинга , открытия точного квантования. Эффект квантового зала также обеспечивает чрезвычайно точное независимое определение константы тонкой структуры , количество фундаментального значения в квантовой электродинамике .

В 1990 году было определено фиксированное традиционное значение r _K-90 = 25 812 .807 Ом для использования в калибровках сопротивления по всему миру. 16 ноября 2018 года 26 -е собрание Генеральной конференции по весам и мерам решило исправить точные значения H (постоянная Планка) и E (элементарный заряд), заменять традиционное значение 1990 года с точным постоянным значением (внутренним стандартом) r _k = ⁠ H / E ² ⁠ = 25 812 .807 45 ... о .

Статус исследования

Дробный эффект квантового зала считается частью точного квантования . Точное квантование в полной общности не полностью изучено, но оно было объяснено как очень тонкое проявление комбинации принципа инвариантности дальности вместе с другой симметрией (см. Аномалии ). Вместо этого эффект целочисленного квантового зала считается решением исследования исследования и понял в сфере формулы TKNN и Chern -Simons Lagrangians .

Дробный эффект квантового зала по -прежнему считается открытой проблемой исследования. Дробный эффект квантового зала также можно понимать как целочисленный эффект квантового зала, хотя и не электронов, но и из композитов заряда, известных как составные фермионы . Другие модели для объяснения дробного квантового зала также существует. В настоящее время это считается открытой проблемой исследования, потому что ни один, не существует единого, подтвержденного и согласованного списка дробных квантовых чисел, ни одна согласованная модель для объяснения их всех, хотя существуют такие претензии в сфере составных фермионов и небелевских Чернов -Симонов Лагранжианцы .

История

В 1957 году Карл Фрош и Линкольн Дерик смогли изготовить первые транзисторы поля диоксида кремния в Bell Labs, первые транзисторы, в которых слив и источник были рядом на поверхности. Впоследствии команда продемонстрировала рабочий MOSFET в Bell Labs 1960. Это позволило физикам изучать поведение электронов в почти идеальном двухмерном газе .

В MOSFET электроны проводится в тонком поверхностном слое, а напряжение « затвора » контролирует количество носителей заряда в этом слое. Это позволяет исследователям исследовать квантовые эффекты путем работы с высокой чистовой техникой при температуре жидкого гелия .

Целостное квантование проводимости зала было первоначально предсказано исследователями Токийского университета Цунея Андо, Юкио Мацумото и Ясутада Умура в 1975 году на основе приблизительного расчета, который они сами не считают правдой. В 1978 году исследователи Университета Гакушуина Джун-Ичи Вакабаяши и Синдзи Каваджи впоследствии наблюдали эффект в экспериментах, проведенных на инверсионном слое МОПЕТА.

В 1980 году Клаус фон Клицинг , работающий в лаборатории с высоким магнитным полем в Гренобле с образцами мосфета на основе кремния, разработанных Майклом Пеппер и Герхардом Дордой, сделал неожиданное открытие того, что сопротивление зала было точно определено. За этот вывод фон Клицинг был удостоен Нобелевской премии 1985 года по физике . Связь между точным квантованием и инвариантностью датчика была впоследствии предложена Робертом Лафлином , который соединил квантовую проводимость с квантованным транспортом заряда в насосе безвесного заряда. Большинство целочисленных экспериментов квантового зала в настоящее время проводится на арсенида галлия гетероструктурах , хотя можно использовать многие другие полупроводниковые материалы. В 2007 году эффект целочисленного квантового зала был зарегистрирован в графене при температуре с высокой температурой в комнатной температуре, и в магний цинка оксид Zno - Mg _x zn _{1- x} O.

Целочисленный эффект квантового зала

Duration: 20 seconds.0:20

Анимированный график, показывающий заполнение уровней Ландау в виде изменений B , и соответствующую позицию на графике коэффициента зала и магнитного поля | только иллюстративно. Уровни распространяются с увеличением поля. Между уровнями наблюдается эффект квантового зала. DOS - это плотность состояний.

Уровни Ландау

Основная статья: уровни Ландау

В двух измерениях, когда классические электроны подвергаются магнитному полю, они следуют круглым орбитам циклотрона. Когда система обрабатывается квантовой механической, эти орбиты квантованы. Чтобы определить значения уровней энергии, должно быть решено уравнение Schrödinger.

Поскольку система подвергается магнитному полю, она должна быть представлена ​​в качестве электромагнитного векторного потенциала в уравнении Шредингера . Рассмотренная система представляет собой электронный газ, который может свободно перемещаться в направлениях X и Y, но плотно ограничен в направлении Z. Затем в направлении z применяется магнитное поле, и в соответствии с датчиком Ландау, потенциал электромагнитного векторного $\mathbf {A} =(0,Bx,0)$ и скалярной потенциал $\phi =0$Полем Таким образом, уравнение Schrödinger для частицы заряда $q$ и эффективная масса $m^{*}$ В этой системе есть:

$\left\{{\frac {1}{2m^{*}}}\left[\mathbf {p} -q\mathbf {A} \right]^{2}+V(z)\right\}\psi (x,y,z)=\varepsilon \psi (x,y,z)$

где $\mathbf {p}$ это канонический импульс, который заменяется оператором $-i\hbar \nabla$ и $\varepsilon$ это общая энергия.

Чтобы решить это уравнение, можно разделить его на два уравнения, поскольку магнитное поле просто влияет на движение вдоль оси x и y. Общая энергия становится тогда, сумма двух вкладов $\varepsilon =\varepsilon _{z}+\varepsilon _{xy}$Полем Соответствующие уравнения в оси z:

$\left[-{\frac {\hbar ^{2}}{2m^{*}}}{\partial ^{2} \over \partial z^{2}}+V(z)\right]u(z)=\varepsilon _{z}u(z)$

Чтобы упростить вещи, решение $V(z)$ считается бесконечным скважином. Таким образом, решения для направления Z являются энергией ${\textstyle \varepsilon _{z}={\frac {n_{z}^{2}\pi ^{2}\hbar ^{2}}{2m^{*}L^{2}}}}$, $n_{z}=1,2,3...$ и волновые функции являются синусоидальными. Для $x$ и $y$ Направления, решение уравнения Шердингера может быть выбрано как произведение плоской волны в $y$-Порация с некоторой неизвестной функцией $x$IE, $\psi _{xy}=u(x)e^{ik_{y}y}$Полем Это потому, что векторный потенциал не зависит от $y$ и оператор импульса ${\hat {p}}_{y}$ Поэтому поездка с гамильтонианом. Заменив это Ансац в уравнение . Шредингера ${\textstyle x_{k_{y}}={\frac {\hbar k_{y}}{eB}}}$.

$\left[-{\frac {\hbar ^{2}}{2m^{*}}}{\partial ^{2} \over \partial x^{2}}+{\frac {1}{2}}m^{*}\omega _{\rm {c}}^{2}(x-l_{B}^{2}k_{y})^{2}\right]u(x)=\varepsilon _{xy}u(x)$

где ${\textstyle \omega _{\rm {c}}={\frac {eB}{m^{*}}}}$ определяется как частота циклотрона и ${\textstyle l_{B}^{2}={\frac {\hbar }{eB}}}$ магнитная длина. Энергии:

$\varepsilon _{xy}\equiv \varepsilon _{n_{x}}=\hbar \omega _{\rm {c}}\left(n_{x}+{\frac {1}{2}}\right)$, $n_{x}=1,2,3...$

И волновые функции для движения в $xy$ плоскость дается продуктом плоской волны в $y$ и Hermite Polynomials, ослабленные гауссовой функцией в $x$, которые являются волновыми функциями гармонического генератора.

От выражения для уровней Ландау замечает, что энергия зависит только от $n_{x}$, не на $k_{y}$Полем Государства с таким же $n_{x}$ но разные $k_{y}$ вырождены.

Плотность состояний

В нулевом поле плотность состояний на единицу поверхности для двумерного электронного газа с учетом дегенерации из-за спина не зависит от энергии

$n_{\rm {2D}}={\frac {m^{*}}{\pi \hbar ^{2}}}$.

Когда поле включается, плотность состояний падает от константа до гребня Дирака , серия Dirac $\delta$ функции, соответствующие разделению уровней Ландау $\Delta \varepsilon _{xy}=\hbar \omega _{\rm {c}}$Полем При конечной температуре, однако, уровни Ландау приобретают ширину ${\textstyle \Gamma ={\frac {\hbar }{\tau _{i}}}}$ существование $\tau _{i}$ время между разбросанными событиями. Обычно предполагается, что точная форма уровня Ландау является гауссовым или лоренцианским профилем.

Другая особенность заключается в том, что волновые функции образуют параллельные полосы в $y$-Прообразование в равной степени вдоль $x$-у, в соответствии с $\mathbf {A}$Полем Поскольку в каком -либо направлении нет ничего особенного $xy$-Пэшин, если векторный потенциал был выбран по -разному, нужно найти круговую симметрию.

Учитывая выборку измерений $L_{x}\times L_{y}$ и применение периодических граничных условий в $y$-направление ${\textstyle k={\frac {2\pi }{L_{y}}}j}$ существование $j$ целое число, можно понять, что каждый параболический потенциал помещается в центре $x_{k}=l_{B}^{2}k$.

Параболические потенциалы вдоль $x$-Ка центрирована в $x_{k}$ с 1 -й волной, соответствующими бесконечно $z$ направление. В $y$-Прообразование там движутся волны самолета.

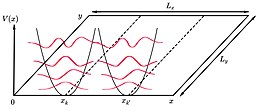
Количество состояний для каждого уровня Ландау и $k$ можно рассчитать по отношению между общим магнитным потоком, который проходит через образец, и магнитным потоком, соответствующим состоянию.

$N_{B}={\frac {\phi }{\phi _{0}}}={\frac {BA}{BL_{y}\Delta x_{k}}}={\frac {A}{2\pi l_{B}^{2}}}{\begin{array}{lcr}&l_{B}&\\&=&\\&&\end{array}}{\frac {AeB}{2\pi \hbar }}{\begin{array}{lcr}&\omega _{\rm {c}}&\\&=&\\&&\end{array}}{\frac {m^{*}\omega _{\rm {c}}A}{2\pi \hbar }}$

Таким образом, плотность состояний на единицу поверхности

$n_{B}={\frac {m^{*}\omega _{\rm {c}}}{2\pi \hbar }}$.

Обратите внимание на зависимость плотности состояний с магнитным полем. Чем больше магнитное поле, тем больше состояний на каждом уровне Ландау. Как следствие, в системе больше ограничений, поскольку занято меньше уровней энергии.

Переписывание последнего выражения как ${\textstyle n_{B}={\frac {\hbar \omega _{\rm {c}}}{2}}{\frac {m^{*}}{\pi \hbar ^{2}}}}$ Понятно, что каждый уровень Ландау содержит столько государств, сколько в 2DEG в $\Delta \varepsilon =\hbar \omega _{\rm {c}}$.

Учитывая тот факт, что электроны являются фермионами , для каждого состояния, доступного на уровнях Ландау, он соответствует двум электронам, один электрон с каждым значением для спина ${\textstyle s=\pm {\frac {1}{2}}}$Полем Однако, если применяется большое магнитное поле, энергии разделились на два уровня из -за магнитного момента, связанного с выравниванием спина с магнитным полем. Разница в энергии ${\textstyle \Delta E=\pm {\frac {1}{2}}g\mu _{\rm {B}}B}$ существование $g$ фактор, который зависит от материала ( $g=2$ для бесплатных электронов) и $\mu _{\rm {B}}$ Бор Магнитон . Знак $+$ принимается, когда вращение параллельно полю и $-$ Когда это антипараллель. Этот факт, называемый спин -расщеплением, подразумевает, что плотность состояний для каждого уровня уменьшается на половину. Обратите внимание, что $\Delta E$ пропорционально магнитному полю, поэтому, чем больше магнитное поле, тем более актуальным является разделение.

Плотность состояний в магнитном поле, пренебрегая расщеплением вращения. (а) Государства в каждом диапазоне $\hbar \omega _{\rm {c}}$ втиснуты в $\delta$-Функция Ландау Уровень. (б) Уровни Ландау имеют ненулевую ширину $\Gamma$ в более реалистичной картине и перекрытии, если $\hbar \omega _{\rm {c}}<\Gamma$Полем (в) уровни становятся различными, когда $\hbar \omega _{\rm {c}}>\Gamma$.

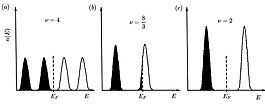
Чтобы получить количество занятых уровней Ландау, один определяет так называемый коэффициент заполнения $\nu$ в качестве отношения между плотностью состояний в 2DEG и плотностью состояний на уровнях Ландау.

$\nu ={\frac {n_{\rm {2D}}}{n_{B}}}={\frac {hn_{\rm {2D}}}{eB}}$

В целом коэффициент заполнения $\nu$ не целое число. Это целое число, когда существует точное количество заполненных уровней Ландау. Вместо этого он становится неинтерегером, когда верхний уровень не полностью занят. В фактических экспериментах один варьирует магнитное поле и фиксирует электронную плотность (а не энергию Ферми!) Или изменяет плотность электронов и фиксирует магнитное поле. Оба случая соответствуют непрерывному изменению коэффициента заполнения $\nu$ и нельзя ожидать $\nu$ быть целым числом. С $n_{B}\propto B$Увеличивая магнитное поле, уровни Ландау поднимаются по энергии, и количество состояний на каждом уровне растут, поэтому меньше электронов занимают верхний уровень, пока он не станет пустым. Если магнитное поле продолжит увеличиваться, в конечном итоге все электроны будут на самом низком уровне Ландау ( $\nu <1$) и это называется магнитным квантовым пределом.

Занятие уровней Ландау в магнитном поле, пренебрегая расщеплением вращения, показывая, как уровень Ферми движется, чтобы поддерживать постоянную плотность электронов. Поля находятся в соотношении $2:3:4$ и дать $\nu =4,{\frac {8}{3}}$ и $2$.

Продольное удельное сопротивление

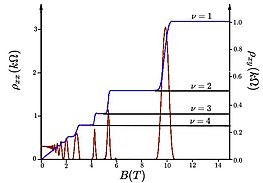
Можно связать коэффициент заполнения с удельным сопротивлением и, следовательно, с проводимостью системы. Когда $\nu$ это целое число, энергия Ферми находится между уровнями Ландау, где нет государств для носителей, поэтому проводимость становится нулевой (считается, что магнитное поле достаточно большое, так что между уровнями Ландау нет перекрытия, в противном случае будет быть немного электронами, и проводимость будет приблизительно $0$) Следовательно, удельное сопротивление тоже становится нулевым (в очень высоких магнитных полях доказано, что продольная проводимость и удельное сопротивление пропорциональны).

С проводимостью $\sigma =\rho ^{-1}$ кто -то находит

$\sigma ={\frac {1}{\det \rho }}{\begin{pmatrix}\rho _{yy}&-\rho _{xy}\\-\rho _{yx}&\rho _{xx}\end{pmatrix}}\;.$

Если продольное удельное сопротивление равна нулю, а походной конечен, тогда $\det \rho \neq 0$Полем Таким образом, как продольная проводимость, так и удельное сопротивление становятся нулевыми.

Вместо этого, когда $\nu$ Полуваленная, энергия Ферми расположена на пике распределения плотности некоторого уровня Ландау. Это означает, что проводимость будет иметь максимум.

Это распределение минимумов и максимумов соответствует «Quantum колебаниям», называемым колебаниями Shubnikov -De Haas , которые становятся более актуальными по мере увеличения магнитного поля. Очевидно, что высота пиков больше, так как магнитное поле увеличивается, поскольку плотность состояний увеличивается с полем, поэтому существует больше носителей, которые способствуют удельности. Интересно заметить, что если магнитное поле очень мало, продольное удельное сопротивление является постоянным, что означает, что классический результат достигнут.

Продольное и поперечное (холл) удельное сопротивление, $\rho _{xx}$ и $\rho _{xy}$, двухмерного электронного газа в зависимости от магнитного поля. Обе вертикальные оси были разделены на квантовую единицу проводимости $e^{2}/h$ (Единицы вводят в заблуждение). Коэффициент заполнения $\nu$ отображается для последних 4 плато.

Поперечное удельное сопротивление

От классической связи поперечного удельного сопротивления ${\textstyle \rho _{xy}={\frac {B}{en_{\rm {2D}}}}}$ и замена ${\textstyle n_{\rm {2D}}=\nu {\frac {eB}{h}}}$ можно узнать квантование поперечного удельного сопротивления и проводимости:

$\rho _{xy}={\frac {h}{\nu e^{2}}}\Rightarrow \sigma =\nu {\frac {e^{2}}{h}}$

Затем можно сделать вывод, что поперечное удельное сопротивление является кратным обратным так называемой квантовой проводимости $e^{2}/h$ Если коэффициент заполнения является целым числом. В экспериментах, однако, наблюдаются плато для целых плато значений заполнения $\nu$, что указывает на то, что на самом деле существуют электронные состояния между уровнями Ландау. Эти состояния локализованы, например, примеси материала, в котором они оказались в ловушке на орбитах, поэтому они не могут способствовать проводимости. Вот почему удельное сопротивление остается постоянным между уровнями Ландау. Опять же, если магнитное поле уменьшается, можно получить классический результат, в котором удельное сопротивление пропорционально магнитному полю.

Эффект фотонного квантового зала

Эффект квантового зала, в дополнение к наблюдаемому в двухмерных электронных системах , может наблюдаться на фотонах. Фотоны не обладают неотъемлемым электрическим зарядом , но благодаря манипуляциям с дискретными оптическими резонаторами искусственное магнитное поле . и фазами связи или фазами на месте можно создать Этот процесс может быть выражен с помощью метафоры фотонов, прыгающих между несколькими зеркалами. Стреляя свет по нескольким зеркалам, фотоны направляются и получают дополнительную фазу, пропорциональную их угловой импульсе . Это создает эффект, как будто они находятся в магнитном поле .

Топологическая классификация

Бабочка Хофстадтера

Целые числа, которые появляются в эффекте зала, являются примерами топологических квантовых чисел . Они известны в математике как первые числа Чернов и тесно связаны с фазой Берри . Поразительной моделью, представляющей большой интерес к этому контексту, является модель Azbel -Harper -Hofstadter, квантовая фазовая диаграмма которого - бабочка Hofstadter, показанная на рисунке. Вертикальная ось - это прочность магнитного поля , а горизонтальная ось является химическим потенциалом , который фиксирует плотность электронов. Цвета представляют проводяности целочисленного зала. Теплые цвета представляют положительные целые числа и холодные цвета отрицательные целые числа. Обратите внимание, однако, что плотность состояний в этих регионах квантованной проводимости зала равна нулю; Следовательно, они не могут произвести плато, наблюдаемые в экспериментах. Фазовая диаграмма является фрактальной и имеет структуру на всех масштабах. На фигуре есть очевидное самопоклонность . При наличии расстройства, которое является источником плато, наблюдаемых в экспериментах, эта диаграмма очень отличается, а фрактальная структура в основном смывается. Кроме того, эксперименты контролируют коэффициент заполнения, а не энергию Ферми. Если эта диаграмма построена как функция коэффициента заполнения, все функции полностью смываются, следовательно, она очень мало общается с фактической физикой залов.

В отношении физических механизмов, примесей и/или конкретных состояний (например, краевых токов) важны как для «целочисленного», так и для «дробного» эффектов. Кроме того, кулоновское взаимодействие также имеет важное значение для дробного эффекта квантового зала . Наблюдаемое сильное сходство между целочисленным и фракционным квантовым эффектом зала объясняется тенденцией электронов образовывать связанные состояния с равномерным количеством кванта магнитного потока, называемого композитными фермионами .

Бор Атома интерпретация константы фон Клицинга

Значение константы фон Клицинг может быть получено уже на уровне одного атома в модели Бора, рассматривая его как эффект одного электронного зала. В то время как во время движения циклотрона на круговой орбите центробежная сила сбалансирована силой Лоренца, ответственной за поперечное напряжение, и эффект зала, можно взглянуть на разницу кулоновских потенциалов в атоме Бора в виде индуцированного напряжения отдельного атома и на напряжение отдельного атома и на Периодическое электронное движение на кругу в качестве тока зала. Определение тока единого атомного зала в качестве скорости одного электронного заряда $e$ производит революции Кеплера с угловой частотой $\omega$

$I={\frac {\omega e}{2\pi }},$

и индуцированное напряжение зала как разница между кулоновским потенциалом водорода в точке электронной орбиты и в бесконечности:

$U=V_{\text{C}}(\infty )-V_{\text{C}}(r)=0-V_{\text{C}}(r)={\frac {e}{4\pi \epsilon _{0}r}}$

Получает квантование определенного сопротивления зала орбита Bohr в стадиях постоянной фон Клицинг как

$R_{\text{Bohr}}(n)={\frac {U}{I}}=n{\frac {h}{e^{2}}}$

который для атома Бора является линейным, но не обратным в целом n .

Релятивистские аналоги

Релятивистские примеры эффекта целочисленного квантового зала и эффекта квантового спин -зала возникают в контексте теории измельчия решетки .

Смотрите также

• Квантовые переходы зала
• Дробный квантовый эффект зала
• Квантовой аномальный эффект зала
• Квантовые клеточные автоматы
• Составные фермионы
• Проводимость квант
• Эффект зала
• Зал зонд
• Графен
• Квантовой эффект спин -холла
• Кулоновский потенциал между двумя токовыми петлями, встроенными в магнитное поле

Дальнейшее чтение

• Доктор Йенни (1987). «Интегральный эффект квантового зала для неспециалистов». Rev. Mod. Физический ​ 59 (3): 781–824. Bibcode : 1987rvmp ... 59..781y . doi : 10.1103/revmodphys.59.781 .
• Д. Ши; Д. Цянь; Л. Рэй; Y. Xia; Ys Hor; RJ Cava; MZ Hasan (2008). «Топологический изолятор дирака в фазе квантового спина». Природа . 452 (7190): 970–974. Arxiv : 0902.1356 . Bibcode : 2008natur.452..970h . doi : 10.1038/nature06843 . PMID   18432240 . S2CID   4402113 .
• 25 лет эффекта квантового зала , К. фон Клицинг, семинар Пуанкаре (Paris-2004). PostScript . PDF .
• Магнитный лабораторный пресс -высвобождение квантового зала, наблюдаемое при комнатной температуре
• Avron, Joseph E.; Осадчи, Даниэль; Seiler, Ruedi (2003). «Топологический взгляд на эффект квантового зала» . Физика сегодня . 56 (8): 38. Bibcode : 2003pht .... 56h..38a . doi : 10.1063/1.1611351 .
• Zyun F. ezawa: Квантовые эффекты зала - теоретический подход поля и связанные с ними темы. World Scientific, Сингапур 2008, ISBN   978-981-270-032-2
• Sankar D. Sarma, Aron Pinczuk : перспектива в квантовых эффектах зала. Wiley-Vch, Weinheim 2004, ISBN   978-0-471-11216-7
• А. Баумгартнер; T. IHN; К. Энсслин; К. Марановский; А. Госсард (2007). «Квантовой переход эффекта зала в экспериментах по сканированию ворот». Физический Преподобный б . 76 (8): 085316. Bibcode : 2007 phrvb..76h5316b . doi : 10.1103/physrevb.76.085316 .
• EI RASHBA и VB TIMOFEEV, Квантовый зал эффект, SOV. Физический - Полупроводники v. 20, с. 617–647 (1986).