Поверхность (математика)

В математике поверхность математическую представляет собой модель общепринятого понятия поверхности . Это обобщение плоскости , но, в отличие от плоскости, оно может быть изогнутым ; это аналогично кривой, обобщающей прямую линию .

Существует несколько более точных определений, зависящих от контекста и математического инструментария, который используется для исследования. Простейшими математическими поверхностями являются плоскости и сферы в евклидовом трехмерном пространстве . Точное определение поверхности может зависеть от контекста. Обычно в алгебраической геометрии поверхность может пересекать сама себя (и может иметь другие особенности ), а в топологии и дифференциальной геометрии — нет.

Поверхность — это топологическое пространство размерности два ; это означает, что движущаяся точка на поверхности может двигаться в двух направлениях (она имеет две степени свободы ). Другими словами, почти вокруг каждой точки существует участок координат , на котором двумерная система координат определена . Например, поверхность Земли напоминает (в идеале) сферу, а широта и долгота обеспечивают на ней двумерные координаты (кроме полюсов и вдоль 180-го меридиана ).

Определения [ править ]

Часто поверхность определяется уравнениями , которым удовлетворяют координаты ее точек. Это случай графика непрерывной функции двух переменных. Множество нулей функции трех переменных представляет собой поверхность, называемую неявной поверхностью . ^[1] Если определяющая функция трех переменных является полиномом , поверхность является алгебраической поверхностью . Например, единичная сфера является алгебраической поверхностью, поскольку ее можно определить неявным уравнением

x^{2}+y^{2}+z^{2}-1=0.

Поверхность также может быть определена как изображение в некотором пространстве размерности не менее 3 непрерывной функции двух переменных (требуются некоторые дополнительные условия, чтобы гарантировать, что изображение не является кривой ). В этом случае говорят, что имеется параметрическая поверхность , которая параметризуется этими двумя переменными, называемыми параметрами . Например, единичная сфера может быть параметризована углами Эйлера , также называемыми долготой $u$ и широтой $v$ :

{\begin{aligned}x&=\cos(u)\cos(v)\\y&=\sin(u)\cos(v)\\z&=\sin(v)\,.\end{aligned}}

Параметрические уравнения поверхностей часто в некоторых точках нерегулярны. Например, все точки единичной сферы, кроме двух, являются образом, согласно приведенной выше параметризации, ровно одной пары углов Эйлера ( по модулю $2 π$ ). Для оставшихся двух точек ( северного и южного полюсов ) cos $v = 0$ , а долгота $u$ может принимать любые значения. Также существуют поверхности, для которых не может существовать единая параметризация, охватывающая всю поверхность. Поэтому часто рассматривают поверхности, параметризованные несколькими параметрическими уравнениями, изображения которых покрывают поверхность. Это формализуется понятием многообразия : в контексте многообразий, обычно в топологии и дифференциальной геометрии , поверхность представляет собой многообразие размерности два; что поверхность является топологическим пространством , в котором каждая точка имеет окрестность , гомеоморфную открытому подмножеству это означает , ( евклидовой плоскости см. Поверхность (топология) и Поверхность (дифференциальная геометрия) ). Это позволяет определять поверхности в пространствах размерностью более трёх и даже абстрактные поверхности , не содержащиеся ни в каком другом пространстве. С другой стороны, это исключает поверхности, имеющие особенности , такие как вершина конической поверхности или точки, где поверхность пересекает сама себя.

В классической геометрии поверхность обычно определяется как геометрическое место точки или линии. Например, сфера — это место точки, находящейся на заданном расстоянии от фиксированной точки, называемой центром; коническая поверхность — это геометрическое место линии, проходящей через фиксированную точку и пересекающей кривую ; поверхность вращения — это геометрическое место кривой, вращающейся вокруг прямой. — Линейчатая поверхность это геометрическое место движущейся линии, удовлетворяющей некоторым ограничениям; в современной терминологии линейчатая поверхность — это поверхность, представляющая собой объединение линий.

Терминология [ править ]

В математике рассматривается несколько видов поверхностей. Таким образом, необходима однозначная терминология, чтобы различать их, когда это необходимо. Топологическая поверхность — это поверхность, являющаяся многообразием размерности два (см. § Топологическая поверхность ). Дифференцируемая поверхность — это поверхность, являющаяся дифференцируемым многообразием (см. § Дифференцируемая поверхность ). Всякая дифференцируемая поверхность является топологической поверхностью, но обратное неверно.

Часто неявно предполагается, что «поверхность» содержится в евклидовом пространстве размерности 3, обычно $R. 3$ . Поверхность, содержащаяся в проективном пространстве, называется проективной поверхностью (см. § Проективная поверхность ). Поверхность, которая не должна быть включена в другое пространство, называется абстрактной поверхностью .

Примеры [ править ]

График на непрерывной функции двух переменных, определенной связном открытом подмножестве $R 2$ является топологической поверхностью . Если функция дифференцируема , то график является дифференцируемой поверхностью .
Плоскость . является одновременно алгебраической поверхностью и дифференцируемой поверхностью Это также управляемая поверхность и поверхность вращения .
( Круговой цилиндр т. е. геометрическое место прямой, пересекающей окружность и параллельной заданному направлению) является алгебраической поверхностью и дифференцируемой поверхностью.
Круговой конус (место прямой, пересекающей окружность и проходящей через фиксированную точку, вершину , находящуюся вне плоскости окружности) — это алгебраическая поверхность, которая не является дифференцируемой поверхностью. Если удалить вершину, оставшаяся часть конуса представляет собой объединение двух дифференцируемых поверхностей.
Поверхность многогранника — это топологическая поверхность, которая не является ни дифференцируемой поверхностью, ни алгебраической поверхностью.
Гиперболический параболоид (график функции $z = xy$ ) — это дифференцируемая поверхность и алгебраическая поверхность. Это также линейчатая поверхность, поэтому ее часто используют в архитектуре .
Двухполостный гиперболоид — это алгебраическая поверхность и объединение двух непересекающихся дифференцируемых поверхностей.

Параметрическая поверхность [ править ]

Параметрическая поверхность — это изображение открытого подмножества евклидовой плоскости (обычно $\mathbb {R} ^{2}$ ) непрерывной функцией в топологическом пространстве , обычно евклидовом пространстве размерности не менее трех. Обычно предполагается, что функция непрерывно дифференцируема , и в этой статье так будет всегда.

В частности, параметрическая поверхность в $\mathbb {R} ^{3}$ задается тремя функциями двух переменных $u$ и $v$ , называемыми параметрами

{\begin{aligned}x&=f_{1}(u,v),\\[4pt]y&=f_{2}(u,v),\\[4pt]z&=f_{3}(u,v)\,.\end{aligned}}

Поскольку изображение такой функции может быть кривой (например, если три функции постоянны относительно $v$ ), требуется дополнительное условие, вообще говоря, что почти для всех значений параметров матрица Якобиана

{\begin{bmatrix}{\dfrac {\partial f_{1}}{\partial u}}&{\dfrac {\partial f_{1}}{\partial v}}\\[6pt]{\dfrac {\partial f_{2}}{\partial u}}&{\dfrac {\partial f_{2}}{\partial v}}\\[6pt]{\dfrac {\partial f_{3}}{\partial u}}&{\dfrac {\partial f_{3}}{\partial v}}\end{bmatrix}}

имеет второй ранг . Здесь «почти все» означает, что значения параметров с рангом два содержат плотное открытое подмножество области параметризации. Для поверхностей в пространстве более высокой размерности условие такое же, за исключением количества столбцов матрицы Якоби.

Касательная плоскость и вектор нормали [ править ]

Точка $p,$ в которой указанная выше матрица Якобиана имеет ранг два, называется регулярной , или, точнее, параметризация называется регулярной в точке $p$ .

Касательная плоскость в регулярной точке $p$ — это единственная плоскость, проходящая через $точку p$ и имеющая направление, параллельное двум векторам-строкам матрицы Якоби. Касательная плоскость — аффинное понятие , поскольку ее определение не зависит от выбора метрики . Другими словами, любое аффинное преобразование отображает касательную плоскость к поверхности в точке, касательную плоскость к образу поверхности в изображении точки.

Нормальная линия в точке поверхности — это единственная линия, проходящая через точку и перпендикулярная касательной плоскости; вектор нормали — это вектор, параллельный нормали.

О других дифференциальных инвариантах поверхностей в окрестности точки см. Дифференциальная геометрия поверхностей .

Неправильная точка и особая точка [ править ]

Точка параметрической поверхности, не являющаяся регулярной, является нерегулярной . Существует несколько видов нерегулярных точек.

Может случиться так, что неправильная точка станет регулярной, если изменить параметризацию. Так обстоит дело с полюсами при параметризации единичной сферы углами Эйлера достаточно поменять местами роли различных координатных осей : для изменения полюсов .

С другой стороны, рассмотрим круговой конус параметрического уравнения

{\begin{aligned}x&=t\cos(u)\\y&=t\sin(u)\\z&=t\,.\end{aligned}}

Вершина конуса является началом координат $(0, 0, 0)$ и получается при $t = 0$ . Это неправильная точка, которая остается нерегулярной, какая бы параметризация ни была выбрана (в противном случае существовала бы единственная касательная плоскость). Такая неправильная точка, касательная плоскость которой не определена, называется особой .

Есть еще один вид особых точек. Существуют точки самопересечения , то есть точки, в которых поверхность пересекает сама себя. Другими словами, это точки, полученные при (как минимум) двух разных значениях параметров.

График двумерной функции [ править ]

Пусть $z = f (x, y)$ — функция двух действительных переменных. Это параметрическая поверхность, параметризованная как

{\begin{aligned}x&=t\\y&=u\\z&=f(t,u)\,.\end{aligned}}

Каждая точка этой поверхности является регулярной, поскольку два первых столбца матрицы Якоби образуют единичную матрицу второго ранга.

Рациональная поверхность [ править ]

Рациональная поверхность — это поверхность, которая может быть параметризована рациональными функциями двух переменных. То есть, если $f i (t, u)$ являются для $i = 0, 1, 2, 3$ полиномами от двух неопределенных, то параметрическая поверхность, определяемая формулой

{\begin{aligned}x&={\frac {f_{1}(t,u)}{f_{0}(t,u)}},\\[6pt]y&={\frac {f_{2}(t,u)}{f_{0}(t,u)}},\\[6pt]z&={\frac {f_{3}(t,u)}{f_{0}(t,u)}}\,,\end{aligned}}

является рациональной поверхностью.

Рациональная поверхность — это алгебраическая поверхность , но большинство алгебраических поверхностей не являются рациональными.

Неявная поверхность [ править ]

Неявная поверхность в евклидовом пространстве (или, в более общем смысле, в аффинном пространстве ) размерности 3 — это множество общих нулей дифференцируемой функции трёх переменных.

f(x,y,z)=0.

Неявный означает, что уравнение неявно определяет одну из переменных как функцию других переменных. Это становится более точным с помощью теоремы о неявной функции : если $f (x 0, y 0, z 0) = 0$ и частная производная по $z$ от $f$ не равна нулю в точке $(x 0, y 0, z 0)$ , то существует дифференцируемая функция $φ (x, y)$ такая, что

f(x,y,\varphi (x,y))=0

в окрестностях $(Икс 0, y 0, z 0)$ . Другими словами, неявная поверхность — это график функции вблизи точки поверхности, где частная производная по $z$ отлична от нуля. Таким образом, неявная поверхность локально имеет параметрическое представление, за исключением точек поверхности, где три частные производные равны нулю.

Правильные точки и касательная плоскость [ править ]

Точка поверхности, в которой хотя бы одна частная производная $f$ не равна нулю, называется регулярной . В такой момент $(x_{0},y_{0},z_{0})$ Касательная плоскость и направление нормали четко определены и могут быть выведены с помощью теоремы о неявной функции из определения, данного выше, в § Касательная плоскость и вектор нормали . Направление нормали — это градиент , то есть вектор

\left[{\frac {\partial f}{\partial x}}(x_{0},y_{0},z_{0}),{\frac {\partial f}{\partial y}}(x_{0},y_{0},z_{0}),{\frac {\partial f}{\partial z}}(x_{0},y_{0},z_{0})\right].

Касательная плоскость определяется неявным уравнением

{\frac {\partial f}{\partial x}}(x_{0},y_{0},z_{0})(x-x_{0})+{\frac {\partial f}{\partial y}}(x_{0},y_{0},z_{0})(y-y_{0})+{\frac {\partial f}{\partial z}}(x_{0},y_{0},z_{0})(z-z_{0})=0.

Особая точка [ править ]

Особая точка неявной поверхности (в $\mathbb {R} ^{3}$ ) — это точка поверхности, где выполняется неявное уравнение и все три частные производные его определяющей функции равны нулю. Следовательно, особые точки являются решениями системы четырех уравнений с тремя неопределенными. Поскольку большинство таких систем не имеют решения, многие поверхности не имеют особых точек. Поверхность, не имеющая особой точки, называется регулярной или неособой .

Исследование поверхностей вблизи их особых точек и классификация особых точек — теория особенностей . Особая точка называется изолированной , если в ее окрестности нет другой особой точки. В противном случае особые точки могут образовать кривую. В частности, это касается самопересекающихся поверхностей.

Алгебраическая поверхность [ править ]

Первоначально алгебраическая поверхность представляла собой поверхность, которую можно было определить неявным уравнением

f(x,y,z)=0,

где $f$ — многочлен от трёх неопределённых с действительными коэффициентами.

Концепция была расширена в нескольких направлениях путем определения поверхностей над произвольными полями и рассмотрения поверхностей в пространствах произвольной размерности или в проективных пространствах . Также рассматриваются абстрактные алгебраические поверхности, не вложенные явно в другое пространство.

Поверхности над произвольными полями [ править ]

полиномы с коэффициентами в любом поле Для определения алгебраической поверхности принимаются . Однако поле коэффициентов многочлена четко не определено, так как, например, многочлен с рациональными коэффициентами также может рассматриваться как многочлен с действительными или комплексными коэффициентами. Поэтому понятие точки поверхности было обобщено следующим образом. ^[2]^{[ нужна страница ]}

Для полинома $f (x, y, z)$ пусть $k$ содержащее коэффициенты, а $K$ — алгебраически замкнутое расширение k $— наименьшее поле ,$ бесконечной степени трансцендентности . ^[3] Тогда точка поверхности является элементом $K 3$ что является решением уравнения

f(x,y,z)=0.

Если многочлен имеет действительные коэффициенты, поле $K$ является комплексным полем и точкой поверхности, принадлежащей $\mathbb {R} ^{3}$ (обычная точка) называется вещественной точкой . Точка, принадлежащая $k 3$ называется рациональной над $k$ или просто рациональной точкой , если $k$ — поле рациональных чисел .

Проекционная поверхность [ править ]

Проективная поверхность в проективном пространстве размерности три — это множество точек, однородные координаты которых являются нулями одного однородного многочлена от четырех переменных. В более общем смысле, проективная поверхность — это подмножество проективного пространства, которое представляет собой проективное разнообразие измерения два .

Проективные поверхности тесно связаны с аффинными поверхностями (то есть обычными алгебраическими поверхностями). От проективной поверхности к соответствующей аффинной поверхности переходят, присваивая ей некоторую координату или неопределенность из определяющих многочленов (обычно последнего). И наоборот, переход от аффинной поверхности к связанной с ней проективной поверхности (называемой проективным завершением ) осуществляется путем усреднения определяющего полинома (в случае поверхностей в пространстве размерности три) или путем усреднения всех полиномов определяющего идеала (для поверхностей в пространстве размерности три). пространство высшего измерения).

В пространствах более высоких измерений [ править ]

Нельзя определить понятие алгебраической поверхности в пространстве размерности выше трёх без общего определения алгебраического многообразия и размерности алгебраического многообразия . Фактически, алгебраическая поверхность — это алгебраическое многообразие размерности два .

Точнее, алгебраическая поверхность в пространстве размерности $n$ представляет собой набор общих нулей не менее $n - 2$ многочленов, но эти многочлены должны удовлетворять дополнительным условиям, проверка которых может быть неочевидной. Во-первых, полиномы не должны определять многообразие или алгебраическое множество более высокой размерности, что обычно имеет место, если один из полиномов находится в идеале, порожденном другими. Обычно $n - 2$ полинома определяют алгебраический набор размерности два или выше. Если размерность равна двум, алгебраическое множество может иметь несколько неприводимых компонентов . Если имеется только один компонент, $n - 2$ полинома определяют поверхность, которая является полным пересечением . Если компонентов несколько, то для выбора конкретного компонента нужны дополнительные полиномы.

Большинство авторов считают алгебраической поверхностью только алгебраические многообразия размерности два, но некоторые считают поверхностями и все алгебраические множества, неприводимые компоненты которых имеют размерность два.

В случае поверхностей в пространстве размерности три каждая поверхность представляет собой полное пересечение, а поверхность определяется одним многочленом, который является неприводимым или нет, в зависимости от того, считаются ли неприводимые алгебраические множества размерности два поверхностями. или нет.

Топологическая поверхность [ править ]

В топологии поверхность обычно определяется как многообразие размерности два. Это означает, что топологическая поверхность — это топологическое пространство , в котором каждая точка имеет окрестность гомеоморфную , открытому подмножеству плоскости евклидовой .

Всякая топологическая поверхность гомеоморфна многогранной поверхности такой, что все грани являются треугольниками . Комбинаторное более высокой размерности ) исследование такого расположения треугольников (или, в более общем смысле, симплексов является исходным объектом алгебраической топологии . Это позволяет характеризовать свойства поверхностей в терминах чисто алгебраических инвариантов , таких как род и группы гомологии .

Классы гомеоморфизма поверхностей полностью описаны (см. Поверхность (топология) ).

Дифференцируемая поверхность [ править ]

В математике дифференциальная геометрия поверхностей с дифференциальной геометрией гладких имеет дело поверхностей с различными дополнительными структурами, чаще всего римановой метрикой .Поверхности широко изучались с различных точек зрения: внешне , в связи с их погружением в евклидово пространство , и внутренне , отражая их свойства, определяемые исключительно расстоянием внутри поверхности, измеренным вдоль кривых на поверхности. Одной из фундаментальных исследуемых концепций является гауссова кривизна , впервые подробно изученная Карлом Фридрихом Гауссом . ^[4] который показал, что кривизна является внутренним свойством поверхности, независимым от ее изометрического вложения в евклидово пространство.

Поверхности естественным образом возникают как графики функций связанные пары переменных , а иногда появляются в параметрической форме или как локусы, с пространственными кривыми . Важную роль в их изучении сыграли группы Ли (в духе Эрлангенской программы ), а именно группы симметрии евклидовой плоскости , сферы и гиперболической плоскости . Эти группы Ли можно использовать для описания поверхностей постоянной гауссовой кривизны; они также являются важным компонентом современного подхода к внутренней дифференциальной геометрии через связи . С другой стороны, внешние свойства, основанные на вложении поверхности в евклидово пространство, также широко изучались. Это хорошо иллюстрируется нелинейными уравнениями Эйлера-Лагранжа в вариационном исчислении : хотя Эйлер разработал уравнения с одной переменной для понимания геодезических , определенных независимо от вложения, одно из основных применений Лагранжа уравнений с двумя переменными было к минимальным поверхностям. , концепция, которую можно определить только с точки зрения вложения.

Фрактальная поверхность [ править ]

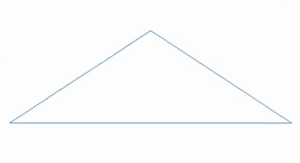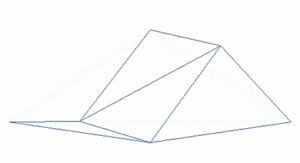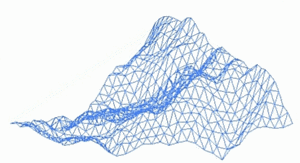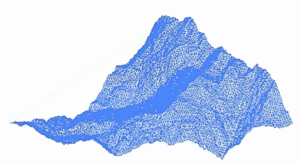
Фрактальный ландшафт или фрактальная поверхность создается с использованием стохастического алгоритма, предназначенного для создания фрактального поведения, имитирующего внешний вид естественной местности . Другими словами, поверхность, полученная в результате процедуры, является не детерминированной, а скорее случайной поверхностью, проявляющей фрактальное поведение. ^[5]

Многие природные явления демонстрируют некоторую форму статистического самоподобия , которую можно смоделировать с помощью фрактальных поверхностей . ^[6] Более того, вариации текстуры поверхности дают важные визуальные подсказки об ориентации и наклонах поверхностей, а использование почти самоподобных фрактальных узоров может помочь создать естественные визуальные эффекты. ^[7]Моделирование шероховатой поверхности Земли посредством дробного броуновского движения было впервые предложено Бенуа Мандельбротом . ^[8]

Поскольку предполагаемым результатом процесса является создание ландшафта, а не математической функции, к таким ландшафтам часто применяются процессы, которые могут повлиять на стационарность и даже общее фрактальное поведение такой поверхности в интересах создания более убедительной модели. пейзаж.

По мнению Р. Р. Ширера , создание естественно выглядящих поверхностей и пейзажей стало важным поворотным моментом в истории искусства, когда различие между геометрическими, созданными компьютером изображениями и естественным, искусственным искусством стало размытым. ^[9] Первое использование фрактального пейзажа в кино было в 1982 году в фильме « Звездный путь 2: Гнев Хана» . Лорен Карпентер усовершенствовала технику Мандельброта для создания инопланетного пейзажа. ^[10]

В компьютерной графике [ править ]

В технических приложениях 3D компьютерной графики ( CAx ), таких как компьютерное проектирование и компьютерное производство , поверхности являются одним из способов представления объектов. Другими способами являются каркасные (линии и кривые) и сплошные тела. Облака точек также иногда используются в качестве временных способов представления объекта с целью использования точек для создания одного или нескольких из трех постоянных представлений.

См. также [ править ]

Area element , площадь дифференциального элемента поверхности.
Координатные поверхности
Гиперповерхность
Периметр , двумерный эквивалент
Многогранная поверхность
Форма
Функция расстояния со знаком
Солидная фигура
Площадь поверхности
Поверхностный патч
Поверхностный интеграл

Примечания [ править ]

^ Здесь «неявное» относится не к свойству поверхности, которое может быть определено другими способами, а к тому, как оно определяется. Таким образом, этот термин является аббревиатурой от «поверхность, определяемая неявным уравнением ».
^ Вейль, Андре (1946), Основы алгебраической геометрии , Публикации коллоквиума Американского математического общества, том. 29, Провиденс, Род-Айленд: Американское математическое общество , стр. 1–363, ISBN. 9780821874622 , МР 0023093 ^{[ нужна страница ]}
^ Бесконечная степень трансцендентности — это техническое условие, позволяющее точно определить понятие общей точки .
^ Гаусс 1902 .
^ «Фрактальная геометрия природы» .
^ Достижения в области мультимедийного моделирования: 13-я Международная конференция по мультимедийному моделированию , Тат-Джен Чам, 2007 г. ISBN 3-540-69428-5 страница [1]
^ Восприятие симметрии человека и его вычислительный анализ Кристофера В. Тайлера, 2002 г. ISBN 0-8058-4395-7 страницы 173–177 [2]
^ Динамика фрактальных поверхностей , авторы семьи Ферейдун и Тамаша Вичека, 1991. ISBN 981-02-0720-4 стр. 45 [3]
^ Ронда Роланд Ширер «Переосмысление образов и метафор» в Языки мозга» книге Альберта М. Галабурды « , 2002 г. ISBN 0-674-00772-7 страниц 351–359 [4]
^ Бриггс, Джон (1992). Фракталы: закономерности хаоса: новая эстетика искусства, науки и природы . Саймон и Шустер. п. 84. ИСБН 978-0671742171 . Проверено 15 июня 2014 г.

Источники [ править ]

Гаусс, Карл Фридрих (1902), Общие исследования искривленных поверхностей 1825 и 1827 годов , Библиотека Принстонского университета

[1] Здесь «неявное» относится не к свойству поверхности, которое может быть определено другими способами, а к тому, как оно определяется. Таким образом, этот термин является аббревиатурой от «поверхность, определяемая неявным уравнением ».

[2] Вейль, Андре (1946), Основы алгебраической геометрии , Публикации коллоквиума Американского математического общества, том. 29, Провиденс, Род-Айленд: Американское математическое общество , стр. 1–363, ISBN. 9780821874622 , МР 0023093 ^{[ нужна страница ]}

[3] Бесконечная степень трансцендентности — это техническое условие, позволяющее точно определить понятие общей точки .

[FOOTNOTEGauss1902-4] Гаусс 1902 .

[5] «Фрактальная геометрия природы» .

[Fractal_landscape_Cham-6] Достижения в области мультимедийного моделирования: 13-я Международная конференция по мультимедийному моделированию , Тат-Джен Чам, 2007 г. ISBN 3-540-69428-5 страница [1]

[7] Восприятие симметрии человека и его вычислительный анализ Кристофера В. Тайлера, 2002 г. ISBN 0-8058-4395-7 страницы 173–177 [2]

[8] Динамика фрактальных поверхностей , авторы семьи Ферейдун и Тамаша Вичека, 1991. ISBN 981-02-0720-4 стр. 45 [3]

[9] Ронда Роланд Ширер «Переосмысление образов и метафор» в Языки мозга» книге Альберта М. Галабурды « , 2002 г. ISBN 0-674-00772-7 страниц 351–359 [4]

[Fractal_landscape_ftpoc-10] Бриггс, Джон (1992). Фракталы: закономерности хаоса: новая эстетика искусства, науки и природы . Саймон и Шустер. п. 84. ИСБН 978-0671742171 . Проверено 15 июня 2014 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]