Проблема Стокса

Задача Стокса в вязкой жидкости, связанная с гармоническими колебаниями плоской жесткой пластины (черный нижний край). Скорость (синяя линия) и перемещение частицы (красные точки) в зависимости от расстояния до стены.

В гидродинамике проблема Стокса , также известная как вторая проблема Стокса или иногда называемая пограничным слоем Стокса или колеблющимся пограничным слоем, представляет собой задачу определения потока, создаваемого колеблющейся твердой поверхностью, названной в честь сэра Джорджа Стокса . Это считается одной из простейших нестационарных задач, имеющей точное решение для уравнений Навье – Стокса . В турбулентном потоке его до сих пор называют пограничным слоем Стокса, но теперь приходится полагаться на эксперименты , численное моделирование или приближенные методы , чтобы получить полезную информацию о потоке.

Описание потока

Рассмотрим бесконечно длинную пластину, колеблющуюся со скоростью $U\cos \omega t$ в $x$ направлении, которое находится в $y=0$ в бесконечной области жидкости, где $\omega$ - частота колебаний. Уравнения несжимаемой жидкости Навье – Стокса сводятся к

${\frac {\partial u}{\partial t}}=\nu {\frac {\partial ^{2}u}{\partial y^{2}}}$

где $\nu$ – кинематическая вязкость . Градиент давления не имеет значения. Исходное состояние отсутствия скольжения на стене равно

$u(0,t)=U\cos \omega t,\quad u(\infty ,t)=0,$

а второе граничное условие связано с тем, что движение при $y=0$ не ощущается на бесконечности. Течение происходит только за счет движения пластины, приложенного градиента давления нет.

Решение

Начальное условие не требуется из-за периодичности. Поскольку и уравнение, и граничные условия линейны, скорость можно записать как действительную часть некоторой комплексной функции.

$u=U\Re \left[e^{i\omega t}f(y)\right]$

потому что $\cos \omega t=\Re e^{i\omega t}$.

Подстановка этого в уравнение в частных производных сводит его к обыкновенному дифференциальному уравнению.

$f''-{\frac {i\omega }{\nu }}f=0$

с граничными условиями

$f(0)=1,\quad f(\infty )=0$

Решение вышеуказанной проблемы заключается

$f(y)=\exp \left[-{\frac {1+i}{\sqrt {2}}}{\sqrt {\frac {\omega }{\nu }}}y\right]$

$u(y,t)=Ue^{-{\sqrt {\frac {\omega }{2\nu }}}y}\cos \left(\omega t-{\sqrt {\frac {\omega }{2\nu }}}y\right)$

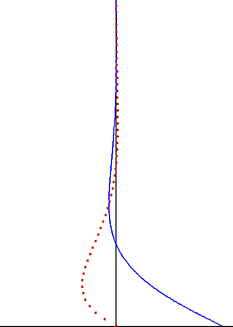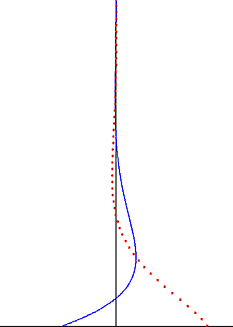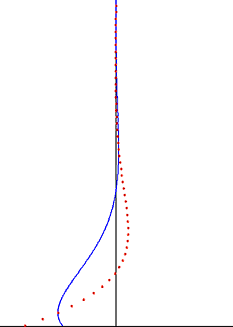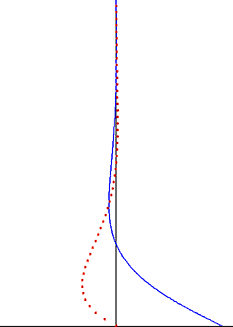
Возмущение, создаваемое колеблющейся пластиной, распространяется как поперечная волна через жидкость, но сильно демпфируется экспоненциальным коэффициентом. Глубина проникновения $\delta ={\sqrt {2\nu /\omega }}$ Эта волна уменьшается с увеличением частоты колебаний, но увеличивается с увеличением кинематической вязкости жидкости.

Сила, действующая на пластину со стороны жидкости на единицу площади, равна

$F=\mu \left({\frac {\partial u}{\partial y}}\right)_{y=0}={\sqrt {\rho \omega \mu }}U\cos \left(\omega t-{\frac {\pi }{4}}\right)$

Существует фазовый сдвиг между колебанием пластины и создаваемой силой.

Колебания завихренности вблизи границы

Важным наблюдением из решения Стокса для осциллирующего стоксова течения является то, что колебания завихренности ограничиваются тонким пограничным слоем и экспоненциально затухают при удалении от стенки. Это наблюдение справедливо и для случая турбулентного пограничного слоя. За пределами пограничного слоя Стокса, который часто составляет основную часть объема жидкости, колебаниями завихренности можно пренебречь. В хорошем приближении колебания скорости потока являются безвихревыми вне пограничного слоя потенциального потока , и к колебательной части движения можно применить теорию . Это значительно упрощает решение этих задач о потоке и часто применяется в областях безвихревого течения звуковых волн и волн на воде .

Жидкость, ограниченная верхней стенкой

Если область жидкости ограничена верхней неподвижной стенкой, расположенной на высоте $y=h$, скорость потока определяется выражением

$u(y,t)={\frac {U}{2(\cosh 2\lambda h-\cos 2\lambda h)}}[e^{-\lambda (y-2h)}\cos(\omega t-\lambda y)+e^{\lambda (y-2h)}\cos(\omega t+\lambda y)-e^{-\lambda y}\cos(\omega t-\lambda y+2\lambda h)-e^{\lambda y}\cos(\omega t+\lambda y-2\lambda h)]$

где $\lambda ={\sqrt {\omega /(2\nu )}}$.

Жидкость, ограниченная свободной поверхностью

Предположим, что протяженность области жидкости равна $0<y<h$ с $y=h$ представляющая собой свободную поверхность. Тогда решение, как показал Цзя-Шунь И в 1968 году. дается

$u(y,t)={\frac {U\cos h/\delta \,\mathrm {cosh} \,h/\delta }{2(\cos ^{2}h/\delta +\mathrm {sinh} ^{2}h/\delta )}}\Re \left\{W+W^{*}-i\mathrm {tanh} \,h/\delta \,\tan h/\delta \,(W-W^{*})\right\},\qquad W=\mathrm {cosh} [(1+i)(h-y)/\delta ]e^{i\omega t}$

где $\delta ={\sqrt {2\nu /\omega }}.$

Течение из-за колеблющегося градиента давления вблизи плоской жесткой пластины

Стоксов пограничный слой из-за синусоидальных колебаний скорости потока в дальней зоне. Горизонтальная скорость обозначена синей линией, а соответствующие горизонтальные отклонения частиц показаны красными точками.

Случай колеблющегося потока в дальней зоне с покоящейся пластиной можно легко построить на основе предыдущего решения для колеблющейся пластины с помощью линейной суперпозиции решений. Рассмотрим равномерное колебание скорости $u(\infty ,t)=U_{\infty }\cos \omega t$ далеко от пластины и исчезающая скорость у пластины $u(0,t)=0$. В отличие от неподвижной жидкости в исходной задаче, градиент давления здесь на бесконечности должен быть гармонической функцией времени. Тогда решение дается формулой

$u(y,t)=U_{\infty }\left[\,\cos \omega t-{\text{e}}^{-{\sqrt {\frac {\omega }{2\nu }}}y}\,\cos \left(\omega t-{\sqrt {\frac {\omega }{2\nu }}}y\right)\right],$

которое равно нулю у стенки y = 0 , что соответствует условию прилипания для покоящейся стенки. Такая ситуация часто встречается в звуковых волнах вблизи твердой стенки или при движении жидкости вблизи морского дна в волнах на воде . Завихренность колеблющегося потока вблизи покоящейся стенки равна завихренности в случае колеблющейся пластины, но противоположного знака.

Задача Стокса в цилиндрической геометрии

Крутильные колебания

Рассмотрим бесконечно длинный цилиндр радиуса $a$ демонстрирующие крутильные колебания с угловой скоростью $\Omega \cos \omega t$ где $\omega$ это частота. Затем скорость после начальной переходной фазы приближается к

$v_{\theta }=a\Omega \ \Re \left[{\frac {K_{1}(r{\sqrt {i\omega /\nu }})}{K_{1}(a{\sqrt {i\omega /\nu }})}}e^{i\omega t}\right]$

где $K_{1}$ – модифицированная функция Бесселя второго рода. Это решение может быть выражено с помощью реального аргумента. как:

${\begin{aligned}v_{\theta }\left(r,t\right)&=\Psi \left\lbrace \left[{\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}r\right)+{\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}r\right)\right]\cos \left(t\right)\right.\\&+\left.\left[{\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}r\right)-{\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}r\right)\right]\sin \left(t\right)\right\rbrace \\\end{aligned}}$

где

$\Psi =\left[{\textrm {kei}}_{1}^{2}\left({\sqrt {R_{\omega }}}\right)+{\textrm {ker}}_{1}^{2}\left({\sqrt {R_{\omega }}}\right)\right]^{-1},$

$\mathrm {kei}$ и $\mathrm {ker}$ являются функциями Кельвина и $R_{\omega }$относится к безразмерному колебательному числу Рейнольдса, определяемому как $R_{\omega }=\omega a^{2}/\nu$, существование $\nu$ кинематическая вязкость.

Осевое колебание

Если цилиндр колеблется в осевом направлении со скоростью $U\cos \omega t$, то поле скорости

$u=U\ \Re \left[{\frac {K_{0}(r{\sqrt {i\omega /\nu }})}{K_{0}(a{\sqrt {i\omega /\nu }})}}e^{i\omega t}\right]$

где $K_{0}$ – модифицированная функция Бесселя второго рода.

Течение Стокса – Куэтта

В течении Куэтта вместо поступательного движения одной из пластин будет совершаться колебание одной плоскости. Если у нас есть нижняя стенка, покоящаяся при $y=0$ и верхняя стена в $y=h$ совершает колебательное движение со скоростью $U\cos \omega t$, то поле скорости имеет вид

$u=U\ \Re \left\{{\frac {\sin ky}{\sin kh}}\right\},\quad {\text{where}}\quad k={\frac {1+i}{\sqrt {2}}}{\sqrt {\frac {\omega }{\nu }}}.$

Сила трения на единицу площади движущейся плоскости равна $-\mu U\Re \{k\cot kh\}$ и на неподвижной плоскости находится $\mu U\Re \{k\csc kh\}$.

См. также

• Задача Рэлея