Переобучение

Рисунок 1. Зеленая линия представляет собой переоснащенную модель, а черная линия представляет собой регуляризованную модель. Хотя зеленая линия лучше всего соответствует данным обучения, она слишком зависит от этих данных и, вероятно, будет иметь более высокий уровень ошибок в новых невидимых данных, что показано точками, обведенными черным контуром, по сравнению с черной линией.

Рисунок 2. Зашумленные (приблизительно линейные) данные аппроксимируются линейной функцией и полиномиальной функцией. Хотя полиномиальная функция идеально подходит, можно ожидать, что линейная функция будет лучше обобщать: если бы две функции использовались для экстраполяции за пределы подогнанных данных, линейная функция должна давать лучшие прогнозы.

Рисунок 3. Синяя пунктирная линия представляет модель с недостаточным оснащением. Прямая линия никогда не может соответствовать параболе. Эта модель слишком проста.

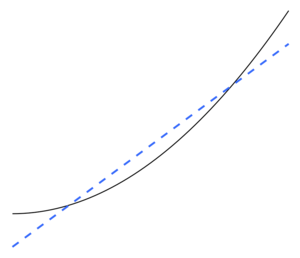
В математическом моделировании переобучение - это «проведение анализа, который слишком близко или точно соответствует определенному набору данных и, следовательно, может не соответствовать дополнительным данным или надежно предсказать будущие наблюдения». Переоснащенная модель — это математическая модель , которая содержит больше параметров , чем можно оправдать данными. В математическом смысле эти параметры представляют степень многочлена . Суть переобучения состоит в том, чтобы неосознанно извлечь часть остаточных отклонений (т. е. шума ), как если бы эти изменения представляли собой основную структуру модели.

Недостаточное соответствие происходит, когда математическая модель не может адекватно отразить основную структуру данных. Недостаточно подобранная модель — это модель, в которой отсутствуют некоторые параметры или термины, которые присутствовали бы в правильно заданной модели. Недостаточное соответствие может произойти, например, при подгонке линейной модели к нелинейным данным. Такая модель будет иметь плохую предсказательную эффективность.

Возможность переобучения существует, поскольку критерий, используемый для выбора модели , не совпадает с критерием, используемым для оценки пригодности модели. Например, модель может быть выбрана путем максимизации ее производительности на некотором наборе обучающих данных , но ее пригодность может определяться ее способностью хорошо работать на невидимых данных; переобучение происходит, когда модель начинает «запоминать» обучающие данные, а не «учиться» делать обобщения на основе тренда.

Крайний пример: если количество параметров равно количеству наблюдений или превышает его, то модель может идеально предсказать обучающие данные, просто запомнив данные целиком. (Иллюстрацию см. на рис. 2.) Однако такая модель обычно дает серьезные сбои при составлении прогнозов.

Переоснащение напрямую связано с ошибкой аппроксимации выбранного класса функций и ошибкой оптимизации процедуры оптимизации. Класс функции, который в соответствующем смысле слишком велик по отношению к размеру набора данных, скорее всего, будет переобучен. Даже если подобранная модель не имеет чрезмерного количества параметров, следует ожидать, что подобранная взаимосвязь будет работать менее эффективно на новом наборе данных, чем на наборе данных, использованном для подбора (явление, иногда называемое сокращением ). частности, значение коэффициента детерминации уменьшится В относительно исходных данных.

Чтобы уменьшить вероятность или количество переобучения, доступно несколько методов (например, сравнение моделей , перекрестная проверка , регуляризация , ранняя остановка , обрезка , байесовские априорные вычисления или отсев ). В основе некоторых методов лежит либо (1) явное наложение штрафов за слишком сложные модели, либо (2) проверка способности модели к обобщению путем оценки ее производительности на наборе данных, не используемых для обучения, который, как предполагается, аппроксимирует типичные невидимые данные, которые модель столкнется.

Статистический

В статистике вывод делается на основе статистической модели , выбранной с помощью некоторой процедуры. Бёрнем и Андерсон в своей часто цитируемой работе по выбору модели утверждают, что во избежание переобучения нам следует придерживаться « принципа бережливости ». Авторы также утверждают следующее.

Переоснащенные модели ... часто не имеют смещения в средствах оценки параметров, но имеют неоправданно большие расчетные (и фактические) отклонения выборки (точность средств оценки низкая по сравнению с тем, чего можно было бы достичь с помощью более экономной модели) . Ложные эффекты лечения, как правило, выявляются, а ложные переменные включаются в переоснащенные модели. ... Модель наилучшего приближения достигается путем правильного балансирования ошибок недостаточного и переоснащения.

Переобучение, скорее всего, станет серьезной проблемой, когда имеется мало теории для проведения анализа, отчасти потому, что тогда существует большое количество моделей для выбора. В книге «Выбор модели и усреднение модели» (2008) об этом говорится так.

Имея набор данных, вы можете подобрать тысячи моделей одним нажатием кнопки, но как выбрать лучшую? При таком большом количестве моделей-кандидатов переобучение представляет собой реальную опасность. Является ли обезьяна, напечатавшая «Гамлета», хорошим писателем?

Регрессия

В регрессионном анализе часто происходит переобучение. есть p В качестве крайнего примера: если в линейной регрессии переменных с p точками данных, подобранная линия может проходить точно через каждую точку. Для логистической регрессии или моделей пропорциональных рисков Кокса существует множество практических правил (например, 5–9, 10 и 10–15 — правило 10 наблюдений на каждую независимую переменную известно как « правило одного из десяти »). В процессе выбора модели регрессии среднеквадратическая ошибка случайной функции регрессии может быть разделена на случайный шум, погрешность аппроксимации и дисперсию оценки функции регрессии. Компромисс смещения и дисперсии часто используется для преодоления моделей переобучения.

При большом наборе объясняющих переменных , которые на самом деле не имеют никакого отношения к прогнозируемой зависимой переменной , некоторые переменные, как правило, будут ошибочно признаны статистически значимыми , и исследователь может, таким образом, сохранить их в модели, тем самым переобучив модель. Это известно как парадокс Фридмана .

Машинное обучение

Рисунок 4. Переобучение/переобучение при обучении с учителем (например, нейронная сеть ). Ошибка обучения показана синим цветом, а ошибка проверки — красным, в зависимости от количества циклов обучения. Если ошибка проверки увеличивается (положительный наклон), а ошибка обучения постоянно уменьшается (отрицательный наклон), то может возникнуть ситуация переобучения. Наилучшей прогнозирующей и подходящей моделью будет та, в которой ошибка проверки имеет глобальный минимум.

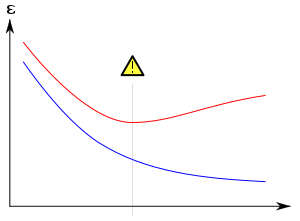
Обычно алгоритм обучения обучается с использованием некоторого набора «обучающих данных»: примерных ситуаций, для которых известен желаемый результат. Цель состоит в том, чтобы алгоритм также хорошо работал при прогнозировании выходных данных при подаче «данных проверки», которые не встречались во время его обучения.

Переоснащение — это использование моделей или процедур, которые нарушают принцип бритвы Оккама , например, путем включения большего количества регулируемых параметров, чем в конечном итоге оптимально, или использования более сложного подхода, чем в конечном итоге оптимально. В качестве примера слишком большого количества настраиваемых параметров рассмотрим набор данных, в котором данные обучения для y могут быть адекватно предсказаны с помощью линейной функции двух независимых переменных. Такая функция требует всего три параметра (точка пересечения и два наклона). Замена этой простой функции новой, более сложной квадратичной функцией или новой, более сложной линейной функцией от более чем двух независимых переменных сопряжена с риском: бритва Оккама подразумевает, что любая данная сложная функция априори менее вероятна, чем любая заданная простая функция. функция. Если вместо простой функции выбрана новая, более сложная функция, и если не было достаточно большого прироста обучающих данных, подходящего для компенсации увеличения сложности, то новая сложная функция «подгоняет» данные, и сложная переоснащенная функция будет вероятно, будет работать хуже, чем более простая функция, на данных проверки вне набора обучающих данных, хотя сложная функция работает так же хорошо или, возможно, даже лучше, на наборе обучающих данных.

При сравнении различных типов моделей сложность нельзя измерить только путем подсчета количества параметров в каждой модели; Необходимо также учитывать выразительность каждого параметра. Например, нетривиально напрямую сравнить сложность нейронной сети (которая может отслеживать криволинейные связи) с m параметрами с регрессионной моделью с n параметрами.

Переобучение особенно вероятно в тех случаях, когда обучение проводилось слишком долго или когда примеры обучения редки, что заставляет учащегося приспосабливаться к очень специфическим случайным особенностям обучающих данных, которые не имеют причинно-следственной связи с целевой функцией . В этом процессе переобучения производительность на обучающих примерах по-прежнему увеличивается, а производительность на невидимых данных ухудшается.

В качестве простого примера рассмотрим базу данных розничных покупок, которая включает купленный товар, покупателя, а также дату и время покупки. Легко построить модель, которая будет идеально соответствовать обучающему набору, используя дату и время покупки для прогнозирования других атрибутов, но эта модель вообще не будет обобщаться на новые данные, потому что прошлые события никогда не повторятся.

Обычно говорят, что алгоритм обучения переобучен по сравнению с более простым, если он более точен в подборе известных данных (рефсайт), но менее точен в прогнозировании новых данных (форсайт). Интуитивно понять переоснащение можно из того факта, что информацию из всего прошлого опыта можно разделить на две группы: информацию, актуальную для будущего, и нерелевантную информацию («шум»). При прочих равных условиях, чем сложнее предсказать критерий (т. е. чем выше его неопределенность), тем больше шума существует в прошлой информации, которую необходимо игнорировать. Проблема заключается в том, какую часть игнорировать. Алгоритм обучения, который может снизить риск подгонки шума, называется « робастным ».

Последствия

Фотография Анны Грэм Лотц, включенная в обучающий набор Stable Diffusion , модели преобразования текста в изображение.

Изображение, созданное Stable Diffusion с использованием подсказки «Энн Грэм Лотц».

Переоснащенные генеративные модели могут давать результаты, практически идентичные экземплярам из их обучающего набора.

Наиболее очевидным последствием переоснащения является низкая производительность набора проверочных данных. К другим негативным последствиям относятся:

• Функция, которая переоснащена, скорее всего, запросит больше информации о каждом элементе в наборе проверочных данных, чем оптимальная функция; сбор этих дополнительных ненужных данных может оказаться дорогостоящим или чреваты ошибками, особенно если каждый отдельный фрагмент информации должен быть собран путем человеческого наблюдения и ввода данных вручную.
• Более сложная, перенастроенная функция, скорее всего, будет менее переносимой, чем простая. С одной стороны, линейная регрессия с одной переменной настолько портативна, что при необходимости ее можно даже выполнить вручную. Другой крайностью являются модели, которые можно воспроизвести только путем точного копирования всей установки исходного моделиста, что затрудняет повторное использование или научное воспроизведение.
• Возможно, удастся восстановить детали отдельных экземпляров обучения из обучающего набора переоборудованной модели машинного обучения. Это может быть нежелательно, если, например, данные обучения включают конфиденциальную личную информацию (PII). Это явление также создает проблемы в области искусственного интеллекта и авторского права : разработчики некоторых генеративных моделей глубокого обучения, таких как Stable Diffusion и GitHub Copilot, подвергаются иску за нарушение авторских прав, поскольку было обнаружено, что эти модели способны воспроизводить определенные элементы, защищенные авторским правом, из данные их обучения.

Средство

Оптимальная функция обычно требует проверки на более крупных или совершенно новых наборах данных. Однако существуют такие методы, как минимальное остовное дерево или время жизни корреляции , которые применяют зависимость между коэффициентами корреляции и временными рядами (шириной окна). Когда ширина окна достаточно велика, коэффициенты корреляции стабильны и больше не зависят от размера ширины окна. Следовательно, корреляционная матрица может быть создана путем расчета коэффициента корреляции между исследуемыми переменными. Топологически эту матрицу можно представить как сложную сеть, в которой визуализируются прямые и косвенные влияния между переменными. Регуляризация отсева также может повысить надежность и, следовательно, уменьшить переобучение за счет вероятностного удаления входных данных в слой.

Недооснащение

Рисунок 5. Красная линия представляет собой недооснащенную модель точек данных, представленных синим цветом. Мы ожидаем увидеть линию в форме параболы, обозначающую кривизну точек данных.

Рисунок 6. Синяя линия представляет собой подобранную модель точек данных, представленных зеленым цветом.

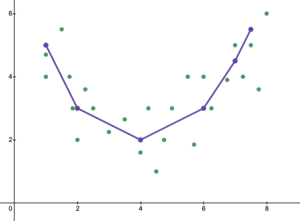
Недостаточное оснащение — это противоположность переобучения, означающее, что статистическая модель или алгоритм машинного обучения слишком упрощены, чтобы точно отразить закономерности в данных. Признаком недостаточного подбора является то, что в текущей используемой модели или алгоритме обнаружена высокая систематическая ошибка и низкая дисперсия (обратная сторона переобучения: низкое смещение и высокая дисперсия ). Это можно получить из компромисса смещения и дисперсии , который представляет собой метод анализа модели или алгоритма на предмет ошибки смещения, ошибки дисперсии и неуменьшаемой ошибки. При высоком смещении и низкой дисперсии модель будет неточно представлять точки данных и, следовательно, не сможет предсказать будущие результаты данных (см. Ошибка обобщения ). Как показано на рисунке 5, линейная линия не может представлять все заданные точки данных, поскольку линия не похожа на кривизну точек. Мы ожидали бы увидеть линию в форме параболы, как показано на рисунках 6 и 1. Если бы мы использовали рисунок 5 для анализа, мы получили бы ложные прогнозные результаты, противоположные результатам, если бы мы проанализировали рисунок 6.

Бернэм и Андерсон утверждают следующее.

...недооснащенная модель будет игнорировать некоторую важную воспроизводимую (т.е. концептуально воспроизводимую в большинстве других образцов) структуру данных и, таким образом, не сможет выявить эффекты, которые фактически подтверждаются данными. В этом случае смещение в средствах оценки параметров часто бывает существенным, а дисперсия выборки недооценивается, причем оба фактора приводят к плохому охвату доверительного интервала. Недооснащенные модели имеют тенденцию упускать из виду важные эффекты лечения в экспериментальных условиях.

Решение проблемы недостаточного оснащения

Есть несколько способов борьбы с недостаточностью:

1. Увеличьте сложность модели. Если модель слишком проста, возможно, придется увеличить ее сложность, добавив больше функций, увеличив количество параметров или используя более гибкую модель. Однако делать это следует осторожно, чтобы избежать переобучения.
2. Используйте другой алгоритм. Если текущий алгоритм не может уловить закономерности в данных, возможно, придется попробовать другой. Например, для некоторых типов данных нейронная сеть может быть более эффективной, чем модель линейной регрессии.
3. Увеличьте объем обучающих данных. Если модель не подходит из-за нехватки данных, может помочь увеличение объема обучающих данных. Это позволит модели лучше отразить основные закономерности в данных.
4. Регуляризация. Регуляризация — это метод, используемый для предотвращения переобучения путем добавления штрафного члена к функции потерь, который препятствует использованию больших значений параметров. Его также можно использовать для предотвращения недостаточной подгонки за счет контроля сложности модели.
5. Ансамблевые методы . Ансамблевые методы объединяют несколько моделей для создания более точного прогноза. Это может помочь уменьшить недостаточное соответствие, позволяя нескольким моделям работать вместе для выявления основных закономерностей в данных.
6. Разработка функций . Разработка функций включает в себя создание новых функций модели из существующих, которые могут быть более актуальными для рассматриваемой проблемы. Это может помочь повысить точность модели и предотвратить подгонку.

Доброкачественное переоснащение

Доброкачественное переоснащение описывает феномен статистической модели, которая, по-видимому, хорошо обобщает невидимые данные, даже если она идеально подходит для зашумленных обучающих данных (т. е. обеспечивает идеальную точность прогнозирования на обучающем наборе). Это явление представляет особый интерес для глубоких нейронных сетей , но изучается с теоретической точки зрения в контексте гораздо более простых моделей, таких как линейная регрессия . В частности, было показано, что чрезмерная параметризация важна для доброкачественного переобучения в этой ситуации. Другими словами, количество направлений в пространстве параметров, не имеющих значения для прогнозирования, должно значительно превышать размер выборки.

См. также

• Компромисс смещения и дисперсии
• Подгонка кривой
• Извлечение данных
• Выбор функции
• Разработка функций
• Парадокс Фридмана
• Ошибка обобщения
• Хорошая посадка
• Время жизни корреляции
• Выбор модели
• Исследовательские степени свободы
• Бритва Оккама
• Основная модель
• Размерность Вапника-Червоненкиса : больший размер VC подразумевает больший риск переобучения.

Ссылки

• Лейнвебер, диджей (2007). «Глупые трюки с майнерами данных». Журнал инвестирования . 16 :15–22. дои : 10.3905/joi.2007.681820 . S2CID   108627390 .
• Тетко, И.В.; Ливингстон, диджей; Луйк, А.И. (1995). «Исследования нейронных сетей. 1. Сравнение переобучения и переобучения» (PDF) . Журнал химической информации и моделирования . 35 (5): 826–833. дои : 10.1021/ci00027a006 .
• Совет 7: Минимизируйте переобучение . Чикко, Д. (декабрь 2017 г.). «Десять быстрых советов по машинному обучению в вычислительной биологии» . Добыча биоданных . 10 (35): 35. дои : 10.1186/s13040-017-0155-3 . ПМК   5721660 . ПМИД   29234465 .

Дальнейшее чтение

• Кристиан, Брайан ; Гриффитс, Том (апрель 2017 г.), «Глава 7: Переоснащение», Алгоритмы, по которым можно жить: информатика человеческих решений , Уильям Коллинз , стр. 149–168, ISBN  978-0-00-754799-9

Внешние ссылки

• Проблема переоснащения данных – Университет Стоуни-Брук
• Что такое «переобучение»? - Эндрю Гельмана Блог
• CSE546: компромисс между смещением линейной регрессии и дисперсией – Вашингтонский университет
• Что такое недостаточное оснащение – IBM