Паритет (физика)

В физике преобразование четности (также называемое инверсией четности ) представляет собой смену знака одной пространственной координаты . В трех измерениях это также может относиться к одновременному изменению знака всех трех пространственных координат ( точечное отражение ):

$$\mathbf {P} :{\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}-x\\-y\\-z\end{pmatrix}}.$$

Его также можно рассматривать как проверку киральности физического явления, поскольку инверсия четности преобразует явление в его зеркальное отражение.

Все фундаментальные взаимодействия элементарных частиц , за исключением слабого взаимодействия , симметричны относительно четности. Как установил эксперимент Ву, США проведенный в Национальном бюро стандартов китайско-американским ученым Чиен-Шиунг Ву , слабое взаимодействие является киральным и, таким образом, обеспечивает средство для исследования киральности в физике. В своем эксперименте Ву воспользовалась контролирующей ролью слабых взаимодействий в радиоактивном распаде атомных изотопов, чтобы установить хиральность слабого взаимодействия.

Напротив, во взаимодействиях, симметричных относительно четности, таких как электромагнетизм в атомной и молекулярной физике, четность служит мощным управляющим принципом, лежащим в основе квантовых переходов.

Матричное представление P (в любом количестве измерений) имеет определитель, равный −1, и, следовательно, отличается от вращения , у которого определитель равен 1. В двумерной плоскости одновременный переворот всех координат в знаке является не преобразованием четности; это то же самое, что поворот на 180° .

В квантовой механике волновые функции, которые не изменяются при преобразовании четности, описываются как четные функции, а те, которые меняют знак при преобразовании четности, являются нечетными функциями.

Простые отношения симметрии

См. Также: Теория представлений SU (2).

При вращении классические геометрические объекты можно разделить на скаляры , векторы и тензоры более высокого ранга. В классической физике физические конфигурации должны трансформироваться под представлениями каждой группы симметрии.

Квантовая теория предсказывает, что состояния в гильбертовом пространстве не обязательно должны трансформироваться при представлениях группы вращений , а только при проективных представлениях . Слово «проективный» относится к тому факту, что если проецировать фазу каждого состояния, при этом мы помним, что общая фаза квантового состояния не наблюдаема, то проективное представление сводится к обычному представлению. Все представления также являются проективными представлениями, но обратное неверно, поэтому условие проективного представления квантовых состояний слабее, чем условие представления классических состояний.

Проективные представления любой группы изоморфны обычным представлениям центрального расширения группы. Например, проективные представления трехмерной группы вращения, которая является специальной ортогональной группой SO (3), являются обычными представлениями специальной унитарной группы SU (2). Проективные представления группы вращения, которые не являются представлениями, называются спинорами , и поэтому квантовые состояния могут превращаться не только в тензоры, но и в спиноры.

Если к этому добавить классификацию по четности, то их можно расширить, например, до понятий

• скаляры ( P = +1 ) и псевдоскаляры ( P = −1 ), которые инвариантны относительно вращения.
• векторы ( P = −1 ) и осевые векторы (также называемые псевдовекторами ) ( P = +1 ), которые оба преобразуются как векторы при вращении.

Можно определить такие отражения , как

$$V_{x}:{\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}-x\\y\\z\end{pmatrix}},$$

которые также имеют отрицательный определитель и образуют допустимое преобразование четности. Затем, комбинируя их с вращениями (или последовательно выполняя x- , y- и z -отражения), можно восстановить определенное ранее преобразование четности. Однако первое приведенное преобразование четности не работает в четном числе измерений, поскольку оно приводит к положительному определителю. В четных измерениях можно использовать только последний пример преобразования четности (или любое отражение нечетного числа координат).

Четность образует абелеву группу $\mathbb {Z} _{2}$ из-за отношения ${\hat {\mathcal {P}}}^{2}={\hat {1}}$. Все абелевы группы имеют только одномерные неприводимые представления . Для $\mathbb {Z} _{2}$, существуют два неприводимых представления: одно четное, ${\hat {\mathcal {P}}}\phi =+\phi$, другой странный, ${\hat {\mathcal {P}}}\phi =-\phi$. Они полезны в квантовой механике. Однако, как будет подробно описано ниже, в квантовой механике состояния не обязательно должны трансформироваться при реальных представлениях четности, а только при проективных представлениях, и поэтому в принципе преобразование четности может вращать состояние на любую фазу .

Представления O (3)

Альтернативный способ записать приведенную выше классификацию скаляров, псевдоскаляров, векторов и псевдовекторов - это использовать пространство представления, в котором преобразуется каждый объект. Это можно выразить в терминах группового гомоморфизма. $\rho$ что определяет представление. Для матрицы $R\in {\text{O}}(3),$

• скаляры: $\rho (R)=1$, тривиальное представление
• псевдоскаляры: $\rho (R)=\det(R)$
• векторы: $\rho (R)=R$, фундаментальное представление
• псевдовекторы: $\rho (R)=\det(R)R.$

Когда представительство ограничено ${\text{SO}}(3)$, скаляры и псевдоскаляры преобразуются одинаково, как и векторы и псевдовекторы.

Классическая механика

Уравнение движения Ньютона $\mathbf {F} =m\mathbf {a}$ (если масса постоянна) приравнивает два вектора и, следовательно, инвариантен относительно четности. Закон гравитации также включает только векторы и, следовательно, также инвариантен относительно четности.

Однако угловой момент $\mathbf {L}$ — аксиальный вектор , $${\begin{aligned}\mathbf {L} &=\mathbf {r} \times \mathbf {p} \\{\hat {P}}\left(\mathbf {L} \right)&=(-\mathbf {r} )\times (-\mathbf {p} )=\mathbf {L} .\end{aligned}}$$

В классической электродинамике плотность заряда $\rho$ скаляр электрического поля, $\mathbf {E}$и текущий $\mathbf {j}$ являются векторами, но магнитное поле, $\mathbf {B}$ является аксиальным вектором. Однако уравнения Максвелла инвариантны относительно четности, поскольку ротор аксиального вектора является вектором.

Влияние пространственной инверсии на некоторые переменные классической физики

Два основных подразделения классических физических переменных имеют либо четную, либо нечетную четность. Способ распределения конкретных переменных и векторов по той или иной категории зависит от того, является ли количество измерений пространства четным или нечетным. Категории четности и нечетности, приведенные ниже для преобразования четности, представляют собой другой, но тесно связанный вопрос.

Ответы, приведенные ниже, верны для трех пространственных измерений. Например, в двумерном пространстве, когда он вынужден оставаться на поверхности планеты, некоторые переменные меняют сторону.

Странный

Классические переменные, знаки которых меняются при инверсии пространства, являются преимущественно векторами. Они включают в себя:

• $h$, спиральность
• $\Phi$, магнитный поток
• $\mathbf {x}$, положение частицы в трехмерном пространстве
• $\mathbf {v}$, скорость частицы
• $\mathbf {a}$, ускорение частицы
• $\mathbf {p}$, линейный импульс частицы
• $\rho \,\mathbf {v}$, массовый расход
• $\mathbf {F}$, сила, действующая на частицу
• $\mathbf {J}$, плотность электрического тока
• $\mathbf {E}$, электрическое поле
• $\mathbf {D}$, поле электрического смещения
• $\mathbf {P}$, электрическая поляризация
• $\mathbf {A}$, электромагнитный векторный потенциал
• $\mathbf {S}$, вектор Пойнтинга (поток электромагнитной энергии).

Даже

Классические переменные, преимущественно скалярные величины, которые не изменяются при пространственной инверсии, включают:

• $t$, время , когда происходит событие
• $m$, масса частицы
• $E$, энергия частицы
• $P$, мощность (скорость совершения работы )
• $\rho$, плотность электрического заряда
• $V$, скалярный электрический потенциал ( напряжение )
• $\rho$, плотность энергии электромагнитного поля
• $\mathbf {L}$, угловой момент частицы (как орбитальной , так и спиновой ) (аксиальный вектор)
• $\mathbf {B}$, магнитное поле (аксиальный вектор)
• $\mathbf {H}$, вспомогательное магнитное поле
• $\mathbf {M}$, намагниченность
• $T_{ij}$тензор напряжений Максвелла .
• Все массы, заряды, константы связи и другие скалярные физические константы, за исключением тех, которые связаны со слабым взаимодействием .

Квантовая механика

Возможные собственные значения

Двумерное представление четности задается парой квантовых состояний, которые переходят друг в друга при четности. Однако это представление всегда можно свести к линейным комбинациям состояний, каждое из которых либо четное, либо нечетное по четности. Говорят, что все неприводимые представления четности одномерны.

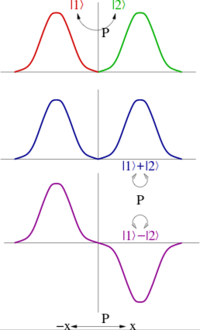
В квантовой механике преобразования пространства-времени действуют на квантовые состояния . Паритетное преобразование, ${\hat {\mathcal {P}}}$, является унитарным оператором , вообще говоря, действующим на состояние $\psi$ следующее: ${\hat {\mathcal {P}}}\,\psi {\left(r\right)}=e^{{i\phi }/{2}}\psi {\left(-r\right)}$.

Тогда необходимо иметь ${\hat {\mathcal {P}}}^{2}\,\psi {\left(r\right)}=e^{i\phi }\psi {\left(r\right)}$, поскольку общая фаза ненаблюдаема. Оператор ${\hat {\mathcal {P}}}^{2}$, который дважды меняет четность состояния, оставляет пространство-время инвариантным, как и внутренняя симметрия, которая вращает свои собственные состояния по фазам $e^{i\phi }$. Если ${\hat {\mathcal {P}}}^{2}$ это элемент $e^{iQ}$ непрерывной группы симметрии фазовых вращений U(1), то $e^{-iQ}$является частью этого U(1) и поэтому также является симметрией. В частности, мы можем определить ${\hat {\mathcal {P}}}'\equiv {\hat {\mathcal {P}}}\,e^{-{iQ}/{2}}$, что также является симметрией, и поэтому мы можем выбрать вызов ${\hat {\mathcal {P}}}'$ наш оператор четности вместо ${\hat {\mathcal {P}}}$. Обратите внимание, что ${{\hat {\mathcal {P}}}'}^{2}=1$ и так ${\hat {\mathcal {P}}}'$ имеет собственные значения $\pm 1$. Волновые функции с собственным значением $+1$ при преобразовании четности являются четными функциями , а собственное значение $-1$ соответствует нечетным функциям. Однако, когда такой группы симметрии не существует, может случиться так, что все преобразования четности имеют некоторые собственные значения, которые являются фазами, отличными от $\pm 1$.

Для электронных волновых функций четные состояния обычно обозначаются индексом g для gerade (немецкий: четный), а нечетные состояния - индексом u для ungerade (немецкий: нечетный). Например, самый низкий энергетический уровень иона молекулы водорода (H ₂ ⁺ ) помечен $1\sigma _{g}$ а следующий ближайший (более высокий) энергетический уровень обозначен $1\sigma _{u}$.

Волновые функции частицы, движущейся во внешний потенциал, который является центросимметричным (потенциальная энергия, инвариантная относительно пространственной инверсии, симметричной началу координат), либо остаются неизменными, либо меняют знак: эти два возможных состояния называются четным состоянием или нечетным состоянием. состояние волновых функций.

Закон сохранения четности частиц гласит, что если изолированный ансамбль частиц имеет определенную четность, то в процессе эволюции ансамбля эта четность остается неизменной. Однако это неверно для бета-распада ядер, поскольку слабое ядерное взаимодействие нарушает четность.

Четность состояний частицы, движущейся в сферически-симметричном внешнем поле, определяется угловым моментом , а состояние частицы определяется тремя квантовыми числами: полной энергией, угловым моментом и проекцией углового момента.

Последствия симметрии четности

Когда четность порождает абелеву группу $\mathbb {Z} _{2}$, всегда можно взять линейные комбинации квантовых состояний так, чтобы они были либо четными, либо нечетными относительно четности (см. рисунок). Таким образом, четность таких состояний равна ±1. Четность многочастичного состояния является произведением четностей каждого состояния; другими словами, четность — это мультипликативное квантовое число.

В квантовой механике гамильтонианы инвариантны ( симметричны ) относительно преобразования четности, если ${\hat {\mathcal {P}}}$ коммутирует с гамильтонианом. В нерелятивистской квантовой механике это происходит для любого скалярного потенциала, т. е. $V=V{\left(r\right)}$, следовательно, потенциал сферически симметричен. Следующие факты могут быть легко доказаны:

• Если $|\varphi \rangle$ и $|\psi \rangle$ иметь одинаковую четность, то $\langle \varphi |{\hat {X}}|\psi \rangle =0$ где ${\hat {X}}$ является оператором позиции .
• Для государства ${\bigl |}{\vec {L}},L_{z}{\bigr \rangle }$ орбитального углового момента ${\vec {L}}$ с проекцией по оси Z $L_{z}$, затем ${\hat {\mathcal {P}}}{\bigl |}{\vec {L}},L_{z}{\bigr \rangle }=\left(-1\right)^{L}{\bigl |}{\vec {L}},L_{z}{\bigr \rangle }$.
• Если ${\bigl [}{\hat {H}},{\hat {\mathcal {P}}}{\bigr ]}=0$, то атомные дипольные переходы происходят только между состояниями противоположной четности.
• Если ${\bigl [}{\hat {H}},{\hat {\mathcal {P}}}{\bigr ]}=0$, то невырожденное собственное состояние ${\hat {H}}$ также является собственным состоянием оператора четности; т. е. невырожденная собственная функция ${\hat {H}}$ либо инвариантен к ${\hat {\mathcal {P}}}$ или изменен знак ${\hat {\mathcal {P}}}$.

Некоторые из невырожденных собственных функций ${\hat {H}}$ на них не влияет (инвариантно) четность ${\hat {\mathcal {P}}}$ а остальные просто меняют знак, когда оператор Гамильтона и оператор четности коммутируют: $${\hat {\mathcal {P}}}|\psi \rangle =c\left|\psi \right\rangle ,$$

где $c$ является константой, собственным значением ${\hat {\mathcal {P}}}$, $${\hat {\mathcal {P}}}^{2}\left|\psi \right\rangle =c\,{\hat {\mathcal {P}}}\left|\psi \right\rangle .$$

Многочастичные системы: атомы, молекулы, ядра.

Общая четность многочастичной системы является произведением четностей одночастичных состояний. Это -1, если нечетное количество частиц находится в состояниях нечетной четности, и +1 в противном случае. Для обозначения четности ядер, атомов и молекул используются разные обозначения.

Атомы

Атомные орбитали имеют четность (−1). ^ℓ , где показатель степени ℓ — азимутальное квантовое число . Четность нечетна для орбиталей p, f, ... с ℓ = 1, 3, ..., а атомное состояние имеет нечетную четность, если нечетное количество электронов занимает эти орбитали. Например, основное состояние атома азота имеет электронную конфигурацию 1s ² 2 с ² 2р ³ и обозначается термином «символ» ⁴ С ^тот , где верхний индекс o обозначает нечетную четность. Однако третий возбужденный член на высоте около 83 300 см ⁻¹ над основным состоянием имеет электронную конфигурацию 1s ² 2 с ² 2р ² 3s имеет четность, поскольку имеется только два 2p-электрона, а его терминальный символ — ⁴ P (без верхнего индекса o).

Молекулы

Полный (вращательно-колебательно-электронно-ядерный спин) электромагнитный гамильтониан любой молекулы коммутирует (или инвариантен) с операцией четности P (или E* в обозначениях, введенных Лонге-Хиггинсом) . ), а его собственным значениям можно присвоить метку симметрии четности + или -, поскольку они четные или нечетные соответственно. Операция четности включает инверсию электронных и ядерных пространственных координат в центре масс молекулы.

Центросимметричные молекулы, находящиеся в равновесии, имеют центр симметрии в средней точке (ядерный центр масс). Сюда входят все гомоядерные двухатомные молекулы , а также некоторые симметричные молекулы, такие как этилен , бензол , тетрафторид ксенона и гексафторид серы . Для центросимметричных молекул точечная группа содержит операцию i , которую не следует путать с операцией четности. Операция i предполагает обращение координат электронного и колебательного смещения в центре масс ядра. Для центросимметричных молекул операция i коммутирует с ровибронным (вращательно-колебательно-электронным) гамильтонианом и может использоваться для обозначения таких состояний. Электронные и колебательные состояния центросимметричных молекул либо не изменяются при операции i , либо меняют знак при операции i . Первые обозначаются индексом g и называются gerade, а вторые обозначаются индексом u и называются унгераде. Полный электромагнитный гамильтониан центросимметричной молекулыне коммутирует с операцией обращения точечной группы i из-за влияния ядерного сверхтонкого гамильтониана. Ядерный сверхтонкий гамильтониан может смешивать вращательные уровни вибронных состояний g и u (так называемое орто-пара -смешивание) и вызывать орто - пара -переходы.

Ядра

В атомных ядрах состояние каждого нуклона (протона или нейтрона) имеет четную или нечетную четность, а конфигурации нуклонов можно предсказать с помощью модели ядерной оболочки . Что касается электронов в атомах, состояние нуклона имеет нечетную общую четность тогда и только тогда, когда число нуклонов в состояниях с нечетной четностью нечетно. Четность обычно записывается как + (четный) или - (нечетный) после значения ядерного спина. Например, к изотопам кислорода относятся ¹⁷ O(5/2+), что означает, что спин равен 5/2 и четность четная. Модель оболочки объясняет это тем, что первые 16 нуклонов спарены так, что каждая пара имеет нулевой спин и четность, а последний нуклон находится в оболочке 1d _5/2 , которая имеет четность, поскольку ℓ = 2 для ад-орбитали.

Квантовая теория поля

Если можно показать, что вакуумное состояние инвариантно относительно четности, ${\hat {\mathcal {P}}}\left|0\right\rangle =\left|0\right\rangle$, гамильтониан инвариантен по четности $\left[{\hat {H}},{\hat {\mathcal {P}}}\right]$ и условия квантования остаются неизменными при четности, то отсюда следует, что каждое состояние имеет хорошую четность и эта четность сохраняется в любой реакции.

Чтобы показать, что квантовая электродинамика инвариантна относительно четности, мы должны доказать, что действие инвариантно и квантование также инвариантно. Для простоты будем считать, что каноническое квантование используется ; тогда вакуумное состояние инвариантно относительно четности по конструкции. Инвариантность действия следует из классической инвариантности уравнений Максвелла. Инвариантность процедуры канонического квантования можно определить, и она, как оказывается, зависит от преобразования оператора уничтожения: $$\mathbf {Pa} (\mathbf {p} ,\pm )\mathbf {P} ^{+}=\mathbf {a} (-\mathbf {p} ,\pm )$$где $\mathbf {p}$ обозначает импульс фотона и $\pm$ относится к его состоянию поляризации. Это эквивалентно утверждению, что фотон имеет нечетную внутреннюю четность . все векторные бозоны Точно так же можно показать, что имеют нечетную внутреннюю четность, а все аксиальные векторы имеют четную внутреннюю четность.

Прямое распространение этих аргументов на скалярные теории поля показывает, что скаляры имеют четность. То есть, ${\mathsf {P}}\phi (-\mathbf {x} ,t){\mathsf {P}}^{-1}=\phi (\mathbf {x} ,t)$, с $$\mathbf {Pa} (\mathbf {p} )\mathbf {P} ^{+}=\mathbf {a} (-\mathbf {p} )$$Это справедливо даже для комплексного скалярного поля. (Подробно о спинорах говорится в статье об уравнении Дирака , где показано, что фермионы и антифермионы имеют противоположную внутреннюю четность.)

С фермионами возникает небольшая сложность, поскольку имеется более одной спиновой группы .

Паритет в стандартной модели

Исправление глобальных симметрий

См. также: (−1) ^Ф

Двойное применение оператора четности оставляет координаты неизменными, а это означает, что P ² должна выступать в качестве одной из внутренних симметрий теории, максимум изменяя фазу состояния. Например, Стандартная модель имеет три глобальные симметрии U(1) равными барионному числу B , лептонному числу L и электрическому заряду Q. с зарядами , Следовательно, оператор четности удовлетворяет условию P ² = и ^{iαB + iβL + iγQ} для некоторого выбора α , β и γ . Этот оператор также не уникален в том смысле, что новый оператор четности P' всегда можно построить, умножив его на внутреннюю симметрию, например P' = P e ^iαB для некоторого α .

Чтобы проверить, всегда ли можно определить оператор четности, удовлетворяющий P ² = 1 , рассмотрим общий случай, когда P ² = Q для некоторой внутренней симметрии Q , присутствующей в теории. Желаемый оператор четности будет P' = P Q ^−1/2 . Если Q является частью непрерывной группы симметрии, то Q ^−1/2 существует, но если он является частью дискретной симметрии , тогда этот элемент не обязательно должен существовать, и такое переопределение может оказаться невозможным.

Стандартная модель демонстрирует (−1) ^Ф симметрия, где F — фермионов оператор числа , подсчитывающий, сколько фермионов находится в состоянии. Поскольку все частицы в Стандартной модели удовлетворяют F = B + L , дискретная симметрия также является частью e ^{яα ( Б + L )} непрерывная группа симметрии. Если оператор четности удовлетворяет P ² = (−1) ^Ф , то его можно переопределить, чтобы задать новый оператор четности, удовлетворяющий P ² = 1 . Но если Стандартную модель расширить за счет включения майорановских нейтрино , у которых F = 1 и B + L = 0 , тогда дискретная симметрия (−1) ^Ф больше не является частью непрерывной группы симметрии, и желаемое переопределение оператора четности не может быть выполнено. Вместо этого он удовлетворяет P ⁴ = 1 , поэтому майорановские нейтрино будут иметь внутреннюю четность ± i .

Четность пиона

В 1954 году статья Уильяма Чиновски и Джека Стейнбергера продемонстрировала, что пион имеет отрицательную четность. Они изучали распад «атома», состоящего из дейтрона ( ²
₁ час ⁺
) и отрицательно заряженный пион (
п ⁻
) в состоянии с нулевым орбитальным моментом $~\mathbf {L} ={\boldsymbol {0}}~$ на два нейтрона ( $n$).

Нейтроны являются фермионами и поэтому подчиняются статистике Ферми – Дирака , из которой следует, что конечное состояние антисимметрично. Используя тот факт, что дейтрон имеет спин один, а спин пиона нулевой, а также антисимметрию конечного состояния, они пришли к выводу, что два нейтрона должны иметь орбитальный угловой момент. $~L=1~.$ Полная четность является произведением внутренней четности частиц и внешней четности сферической гармонической функции. $~\left(-1\right)^{L}~.$ Поскольку в этом процессе орбитальный момент изменяется от нуля до единицы, то для сохранения полной четности произведения собственных четностей начальной и конечной частиц должны иметь противоположный знак. Ядро дейтрона состоит из протона и нейтрона, поэтому, используя вышеупомянутое соглашение, что протоны и нейтроны имеют внутреннюю четность, равную $~+1~$ они утверждали, что четность пиона равна минус произведению четностей двух нейтронов, разделенному на четность протона и нейтрона в дейтроне, явно ${\textstyle {\frac {(-1)(1)^{2}}{(1)^{2}}}=-1~,}$ из чего они сделали вывод, что пион — псевдоскалярная частица .

Нарушение четности

Смотрите также: эксперимент Ву

P-симметрия: часы, построенные по зеркальному изображению, ведут себя как зеркальное изображение исходных часов.

P-асимметрия: часы, построенные по зеркальному изображению, но не ведут себя как зеркальное изображение исходных часов.

Хотя четность сохраняется в электромагнетизме и гравитации , она нарушается в слабых взаимодействиях и, возможно, в некоторой степени, в сильных взаимодействиях . Стандартная модель включает нарушение четности , выражая слабое взаимодействие как киральное калибровочное взаимодействие. В заряженных слабых взаимодействиях в Стандартной модели участвуют только левые компоненты частиц и правые компоненты античастиц. Это означает, что четность не является симметрией нашей Вселенной, если только не существует скрытого зеркального сектора , в котором четность нарушается противоположным образом.

Малоизвестный эксперимент 1928 года, предпринятый Р.Т. Коксом , Г.К. Макилрайтом и Б. Куррелмейером, фактически выявил нарушение четности при слабых распадах , но, поскольку соответствующие концепции еще не были разработаны, эти результаты не оказали никакого влияния. В 1929 году Герман Вейль без каких-либо доказательств исследовал существование двухкомпонентной безмассовой частицы со спином, равным половине. Эта идея была отвергнута Паули , поскольку она подразумевала нарушение четности.

К середине 20-го века несколько ученых предположили, что паритет может не сохраняться (в разных контекстах), но без веских доказательств эти предположения не считались важными. Затем, в 1956 году, тщательный обзор и анализ физиков-теоретиков Цунг-Дао Ли и Чэнь-Нин Янга пошел дальше, показав, что, хотя сохранение четности было подтверждено при распадах в результате сильного или электромагнитного взаимодействия , оно не было проверено в слабом взаимодействии . Они предложили несколько возможных прямых экспериментальных испытаний. Их по большей части игнорировали, но Ли смог убедить своего коллегу из Колумбийского университета Чиен-Шиунг Ву попробовать это. Ей требовалось специальное криогенное оборудование и опыт, поэтому эксперимент провели в Национальном бюро стандартов .

Ву , Эмблер , Хейворд, Хоппс и Хадсон (1957) обнаружили явное нарушение сохранения четности при бета-распаде кобальта-60 . Когда эксперимент подходил к концу и продолжалась двойная проверка, Ву проинформировала Ли и Яна об их положительных результатах и, заявив, что результаты требуют дальнейшего изучения, попросила их сначала не публиковать результаты. Однако Ли представил результаты своим коллегам из Колумбийского университета 4 января 1957 года на «пятничном обеде» на физическом факультете Колумбийского университета. Трое из них, Р. Л. Гарвин , Л. М. Ледерман и Р. М. Вайнрих, модифицировали существующий циклотронный эксперимент и немедленно подтвердили нарушение четности. Они отложили публикацию своих результатов до тех пор, пока группа Ву не была готова, и обе статьи появились одна за другой в одном физическом журнале.

Открытие нарушения четности объяснило выдающуюся τ–θ загадку в физике каонов .

В 2010 году сообщалось, что физики, работающие с релятивистским коллайдером тяжелых ионов, создали недолговечный пузырь, нарушающий симметрию четности, в кварк-глюонной плазме . Эксперимент, проведенный несколькими физиками коллаборации STAR , предположил, что четность может нарушаться и при сильном взаимодействии. Предсказывается, что это локальное нарушение четности проявляется в виде кирального магнитного эффекта .

Внутренняя четность адронов

Каждой частице можно приписать внутреннюю четность, пока природа сохраняет четность. Хотя слабые взаимодействия этого не делают, все же можно приписать четность любому адрону , исследуя реакцию сильного взаимодействия, которая его производит, или посредством распадов, не связанных со слабым взаимодействием, таких как распад ро-мезона на пионы .

См. также

• C-симметрия
• нарушение CP
• Электрослабая теория
• Зеркальная материя
• Молекулярная симметрия
• Т-симметрия

Ссылки

Сноски

Цитаты

Источники

• Перкинс, Дональд Х. (2000). Введение в физику высоких энергий . Издательство Кембриджского университета. ISBN  9780521621960 .
• Соцци, М.С. (2008). Дискретные симметрии и CP-нарушение . Издательство Оксфордского университета . ISBN  978-0-19-929666-8 .
• Биги, II; Санда, А.И. (2000). Нарушение КП . Кембриджские монографии по физике элементарных частиц, ядерной физике и космологии. Издательство Кембриджского университета . ISBN  0-521-44349-0 .
• Вайнберг, С. (1995). Квантовая теория полей . Издательство Кембриджского университета . ISBN  0-521-67053-5 .