Сигмовидная функция

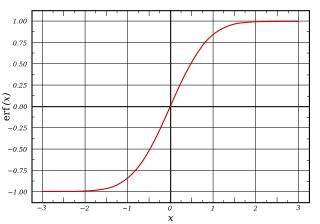
Сигмовидная функция — это любая математическая функция которой , график имеет характерную S-образную или сигмовидную кривую .

Типичным примером сигмовидной функции является логистическая функция, показанная на первом рисунке и определяемая формулой: ^[1]

\sigma (x)={\frac {1}{1+e^{-x}}}={\frac {e^{x}}{1+e^{x}}}=1-\sigma (-x).

Другие стандартные сигмовидные функции приведены в разделе «Примеры» . В некоторых областях, особенно в контексте искусственных нейронных сетей , термин «сигмовидная функция» используется как псевдоним логистической функции.

Особые случаи сигмовидной функции включают кривую Гомпертца (используется в системах моделирования, которые насыщаются при больших значениях x) и кривую Оги (используется в водосбросе некоторых плотин ). Сигмовидные функции имеют область определения всех действительных чисел , при этом возвращаемое значение (ответ) обычно монотонно увеличивается , но может уменьшаться. Сигмовидные функции чаще всего отображают возвращаемое значение (ось Y) в диапазоне от 0 до 1. Другой часто используемый диапазон — от –1 до 1.

широкое разнообразие сигмовидных функций, включая логистические и гиперболические функции тангенса использовалось В качестве функции активации искусственных нейронов . Сигмовидные кривые также распространены в статистике как кумулятивные функции распределения (которые идут от 0 до 1), такие как интегралы логистической плотности , нормальной плотности и Стьюдента t -функций плотности вероятности . Логистическая сигмоидальная функция обратима, а ее обратная функция — логит -функция.

Определение

Сигмоидальная функция — это действительная функция ограниченная дифференцируемая , которая определена для всех действительных входных значений и имеет неотрицательную производную в каждой точке. ^[1] ^[2] и ровно одна точка перегиба .

Характеристики

В общем, сигмовидная функция монотонна и имеет первую производную , имеющую колоколообразную форму . И наоборот, интеграл любой непрерывной неотрицательной колоколообразной функции (с одним локальным максимумом и без локального минимума, если только она не вырождена) будет сигмоидальным. Таким образом, кумулятивные функции распределения для многих распространенных распределений вероятностей являются сигмоидальными. Одним из таких примеров является функция ошибок , которая связана с кумулятивной функцией распределения нормального распределения ; другой — функция арктанса , которая связана с кумулятивной функцией распределения распределения Коши .

Сигмовидная функция ограничена парой горизонтальных асимптот как $x\rightarrow \pm \infty$ .

Сигмовидная функция является выпуклой для значений, меньших определенной точки, и вогнутой для значений, превышающих эту точку: во многих примерах здесь эта точка равна 0.

Примеры

Сравнение некоторых сигмовидных функций. На рисунке все функции нормированы таким образом, что их наклон в начале координат равен 1.

Логистическая функция $f(x)={\frac {1}{1+e^{-x}}}$
Гиперболический тангенс (смещенная и масштабированная версия логистической функции, приведенная выше) $f(x)=\tanh x={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$
Функция арктангенса $f(x)=\arctan x$
функция Гудермана $f(x)=\operatorname {gd} (x)=\int _{0}^{x}{\frac {dt}{\cosh t}}=2\arctan \left(\tanh \left({\frac {x}{2}}\right)\right)$
Функция ошибки $f(x)=\operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,dt$
Обобщенная логистическая функция $f(x)=\left(1+e^{-x}\right)^{-\alpha },\quad \alpha >0$
плавного шага Функция $f(x)={\begin{cases}{\displaystyle \left(\int _{0}^{1}\left(1-u^{2}\right)^{N}du\right)^{-1}\int _{0}^{x}\left(1-u^{2}\right)^{N}\ du},&|x|\leq 1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\quad N\in \mathbb {Z} \geq 1$
Некоторые алгебраические функции , например $f(x)={\frac {x}{\sqrt {1+x^{2}}}}$
и в более общей форме ^[3] $f(x)={\frac {x}{\left(1+|x|^{k}\right)^{1/k}}}$
С точностью до сдвигов и масштабирования многие сигмоиды представляют собой частные случаи $f(x)=\varphi (\varphi (x,\beta ),\alpha ),$ где $\varphi (x,\lambda )={\begin{cases}(1-\lambda x)^{1/\lambda }&\lambda \neq 0\\e^{-x}&\lambda =0\\\end{cases}}$ является обратным отрицательному преобразованию Бокса – Кокса и $\alpha <1$ и $\beta <1$ являются параметрами формы. ^[4]
Функция плавного перехода ^[5] нормализовано до (-1,1):

${\begin{aligned}f(x)&={\begin{cases}{\displaystyle {\frac {2}{1+e^{-2m{\frac {x}{1-x^{2}}}}}}-1},&|x|<1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\\&={\begin{cases}{\displaystyle \tanh \left(m{\frac {x}{1-x^{2}}}\right)},&|x|<1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\end{aligned}}$ используя упомянутый выше гиперболический тангенс. Здесь, $m$ — свободный параметр, кодирующий наклон при $x=0$ , который должен быть больше или равен ${\sqrt {3}}$ потому что любое меньшее значение приведет к получению функции с несколькими точками перегиба, которая, следовательно, не является настоящей сигмоидой. Эта функция необычна, поскольку она фактически достигает предельных значений -1 и 1 в конечном диапазоне, а это означает, что ее значение постоянно при -1 для всех $x\leq -1$ и по 1 для всех $x\geq 1$ . Тем не менее, оно гладкое (бесконечно дифференцируемое, $C^{\infty }$ ) везде , в том числе и в $x=\pm 1$ .

Приложения

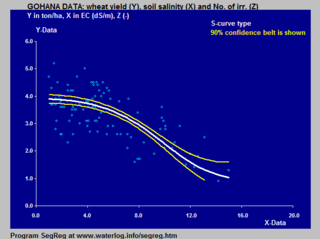
Многие естественные процессы, такие как кривые обучения сложных систем , демонстрируют прогресс от малого начала, которое со временем ускоряется и приближается к кульминации. Когда конкретная математическая модель отсутствует, часто используется сигмовидная функция. ^[6]

Модель Ван Генухтена-Гупты основана на перевернутой S-кривой и применяется к реакции урожайности сельскохозяйственных культур на засоление почвы .

Примеры применения логистической S-кривой к реакции урожайности сельскохозяйственных культур (пшеница) как на засоленность почвы, так и на глубину уровня грунтовых вод в почве показаны при моделировании реакции сельскохозяйственных культур в сельском хозяйстве .

В искусственных нейронных сетях иногда вместо этого для повышения эффективности используются негладкие функции; они известны как твердые сигмоиды .

При обработке аудиосигнала сигмовидные функции используются в качестве формирователя волны передаточных функций для имитации звука аналоговой схемы ограничения . ^[7]

В биохимии и фармакологии уравнения Хилла представляют и Хилла-Лэнгмюра собой сигмовидные функции.

В компьютерной графике и рендеринге в реальном времени некоторые сигмовидные функции используются для плавного смешивания цветов или геометрии между двумя значениями, без видимых швов или разрывов.

Кривые титрования между сильными кислотами и сильными основаниями имеют сигмовидную форму из-за логарифмического характера шкалы рН .

Логистическую функцию можно эффективно рассчитать, используя Unums типа III . ^[8]

См. также

Ступенчатая функция – Линейная комбинация индикаторных функций реальных интервалов
Функция знака – математическая функция, возвращающая -1, 0 или 1.
Ступенчатая функция Хевисайда - Индикаторная функция положительных чисел
Логистическая регрессия - Статистическая модель для бинарной зависимой переменной.
Логит - функция в статистике.
Функция Softplus – функция активации.
Модифицированный гиперболический тангенс Соболевой – Математическая функция активации в анализе данных
Функция Softmax – плавная аппроксимация максимума однократного аргумента
Функция Swish – математическая функция активации при анализе данных.
Распределение Вейбулла – непрерывное распределение вероятностей
Статистика Ферми – Дирака - Статистическое описание поведения фермионов.

Ссылки

^ Jump up to: ^а ^б Хан, Джун; Мораг, Клаудио (1995). «Влияние параметров сигмовидной функции на скорость обучения обратного распространения ошибки» . В Мире, Хосе; Сандовал, Франциско (ред.). От естественных к искусственным нейронным вычислениям . Конспекты лекций по информатике. Том. 930. стр. 195–201 . дои : 10.1007/3-540-59497-3_175 . ISBN 978-3-540-59497-0 .
^ Лин, Ибэй; Он, Бин (декабрь 1993 г.). «Энтропийный анализ моделей биологического роста» . Транзакции IEEE по биомедицинской инженерии . 40 (12): 1193–2000. дои : 10.1109/10.250574 . PMID 8125495 .
^ Даннинг, Эндрю Дж.; Кенслер, Дженнифер; Кудевиль, Лоран; Байе, Фабрис (28 декабря 2015 г.). «Некоторые расширения непрерывных методов определения иммунологических коррелятов защиты» . Методология медицинских исследований BMC . 15 (107): 107. дои : 10.1186/s12874-015-0096-9 . ПМК 4692073 . ПМИД 26707389 .
^ "grex --- Обозреватель кривой роста" . Гитхаб . 09.07.2022. Архивировано из оригинала 25 августа 2022 г. Проверено 25 августа 2022 г.
^ ЭпсилонДельта (16 августа 2022 г.). «Функция плавного перехода в одном измерении | Серия функций плавного перехода, часть 1» . 13:29/14:04 – через www.youtube.com.
^ Гиббс, Марк Н.; Маккей, Д. (ноябрь 2000 г.). «Вариационные гауссовские классификаторы процессов». Транзакции IEEE в нейронных сетях . 11 (6): 1458–1464. дои : 10.1109/72.883477 . ПМИД 18249869 . S2CID 14456885 .
^ Смит, Джулиус О. (2010). Физическая обработка аудиосигнала (изд. 2010 г.). Издательство W3K. ISBN 978-0-9745607-2-4 . Архивировано из оригинала 14 июля 2022 г. Проверено 28 марта 2020 г.
^ Густафсон, Джон Л .; Ёнемото, Исаак (12 июня 2017 г.). «Преодоление чисел с плавающей запятой в собственной игре: положительная арифметика» (PDF) . Архивировано (PDF) из оригинала 14 июля 2022 г. Проверено 28 декабря 2019 г.

Дальнейшее чтение

Митчелл, Том М. (1997). Машинное обучение . WCB МакГроу – Хилл . ISBN 978-0-07-042807-2 . . (Примечание. В частности, см. «Главу 4: Искусственные нейронные сети» (в частности, стр. 96–97), где Митчелл использует слова «логистическая функция» и «сигмовидная функция» как синонимы - эту функцию он также называет «функцией сжатия». – а сигмовидная (она же логистическая) функция используется для сжатия выходных данных «нейронов» в многослойных нейронных сетях.)
Хамфрис, Марк. «Непрерывный вывод, сигмовидная функция» . Архивировано из оригинала 14 июля 2022 г. Проверено 14 июля 2022 г. (Примечание. Свойства сигмовидной кишки, в том числе то, как она может перемещаться по осям и как может трансформироваться ее область.)

Внешние ссылки

«Подбор логистических S-кривых (сигмоид) к данным с использованием SegRegA» . Архивировано из оригинала 14 июля 2022 г.

[Han-Morag_1995-1] Jump up to: ^а ^б Хан, Джун; Мораг, Клаудио (1995). «Влияние параметров сигмовидной функции на скорость обучения обратного распространения ошибки» . В Мире, Хосе; Сандовал, Франциско (ред.). От естественных к искусственным нейронным вычислениям . Конспекты лекций по информатике. Том. 930. стр. 195–201 . дои : 10.1007/3-540-59497-3_175 . ISBN 978-3-540-59497-0 .

[yibei-2] Лин, Ибэй; Он, Бин (декабрь 1993 г.). «Энтропийный анализ моделей биологического роста» . Транзакции IEEE по биомедицинской инженерии . 40 (12): 1193–2000. дои : 10.1109/10.250574 . PMID 8125495 .

[Dunning-Kensler-Coudeville-Bailleux_2015-3] Даннинг, Эндрю Дж.; Кенслер, Дженнифер; Кудевиль, Лоран; Байе, Фабрис (28 декабря 2015 г.). «Некоторые расширения непрерывных методов определения иммунологических коррелятов защиты» . Методология медицинских исследований BMC . 15 (107): 107. дои : 10.1186/s12874-015-0096-9 . ПМК 4692073 . ПМИД 26707389 .

[grex-4] "grex --- Обозреватель кривой роста" . Гитхаб . 09.07.2022. Архивировано из оригинала 25 августа 2022 г. Проверено 25 августа 2022 г.

[5] ЭпсилонДельта (16 августа 2022 г.). «Функция плавного перехода в одном измерении | Серия функций плавного перехода, часть 1» . 13:29/14:04 – через www.youtube.com.

[Gibbs_2000-6] Гиббс, Марк Н.; Маккей, Д. (ноябрь 2000 г.). «Вариационные гауссовские классификаторы процессов». Транзакции IEEE в нейронных сетях . 11 (6): 1458–1464. дои : 10.1109/72.883477 . ПМИД 18249869 . S2CID 14456885 .

[Smith_2010-7] Смит, Джулиус О. (2010). Физическая обработка аудиосигнала (изд. 2010 г.). Издательство W3K. ISBN 978-0-9745607-2-4 . Архивировано из оригинала 14 июля 2022 г. Проверено 28 марта 2020 г.

[Gustafson-Yonemoto_2017-8] Густафсон, Джон Л .; Ёнемото, Исаак (12 июня 2017 г.). «Преодоление чисел с плавающей запятой в собственной игре: положительная арифметика» (PDF) . Архивировано (PDF) из оригинала 14 июля 2022 г. Проверено 28 декабря 2019 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]