Комбинаторность
В музыке, использующей технику двенадцати тонов , комбинаторность - это качество, присущее двенадцатитоновым рядам тонов , при котором каждая часть ряда и пропорциональное количество его преобразований объединяются, образуя агрегаты (все двенадцать тонов). [1] Точно так же, как высоты совокупности, созданной тональным рядом, не обязательно должны возникать одновременно, так и высоты комбинаторно созданной совокупности не обязательно должны возникать одновременно. Арнольд Шенберг , создатель двенадцатитоновой техники, часто комбинировал P-0/I-5, чтобы создать «две совокупности, между первыми гексахордами каждого и вторыми гексахордами каждого соответственно». [1]
Комбинаториальность — это побочный эффект производных строк , когда исходный сегмент или набор можно объединить с его преобразованиями (T,R,I,RI) для создания целой строки. «Деривация относится к процессу, посредством которого, например, начальный трихорд ряда может быть использован для получения нового, «производного» ряда, используя стандартные двенадцатитоновые операции транспозиции , инверсии , ретроградной и ретроградной инверсии . " [2]
Комбинаторные свойства не зависят от порядка нот внутри набора, а только от содержания набора, причем комбинаторность может существовать между тремя тетрахордальными и между четырьмя трихордальными наборами, а также между парами гексахордов. [3] и шесть диад . [4] Дополнением . в этом контексте является половина комбинаторного набора классов высоты тона и, как правило, это «другая половина» любой пары, включая наборы классов высоты тона, текстуры или диапазон высоты тона
Определение [ править ]
Чаще всего дополнением является разделение коллекций тональных классов на два взаимодополняющих набора, один из которых содержит классы тонального тона, которых нет в другом. [1] В более строгом смысле комплементация — это «процесс объединения сущностей по обе стороны от центра симметрии». [5]

Термин «комбинаторный», по-видимому, впервые был применен к двенадцатитоновой музыке Милтоном Бэббитом в 1950 году. [7] когда он опубликовал рецензию на Рене Лейбовица книги «Шенберг и его школа» и «Что такое музыка двенадцати звуков?» [8] Бэббит также ввел термин « производная строка» . [2]
Гексахордальная комбинаторность [ править ]

12-тоновый ряд имеет гексахордальную комбинаторность с другим 12-тоновым рядом, если их соответствующие первые (а также вторые, поскольку 12-тоновый ряд сам по определению образует агрегат) гексахорды образуют агрегат.
Выделяют четыре основных типа комбинаторности. Гексахорд может быть:
- Простая комбинаторика ( транспозиция )
- Ретроградный комбинаторный ( ретроградный )
- Инверсионная комбинаторика ( инверсия )
- Ретроградно-инверсионная комбинаторика ( ретроградно-инверсия )
и таким образом:
- Полукомбинаторный (по одному из вышеперечисленных)
- Всекомбинаторный (по всем)
Первичная (транспозиционная) комбинаторность гексахорды относится к свойству гексахорды, посредством которого он образует совокупность с одной или несколькими своими транспозициями. Альтернативно, транспозиционная комбинаториальность - это отсутствие общих классов высоты звука между гексахордом и одной или несколькими его транспозициями. Например, 0 2 4 6 8 t и его транспонирование на полутон вверх (+1): 1 3 5 7 9 e не имеют общих нот.
Ретроградная гексахордальная комбинаторность считается тривиальной, поскольку любой ряд обладает ретроградной гексахордальной комбинаторностью сам с собой ( все тоновые ряды обладают ретроградной комбинаторностью).
Инверсионная комбинаторность — это связь между двумя строками: основной строкой и ее инверсией. Первая половина основного ряда, или шесть нот, — это последние шесть нот инверсии, хотя и не обязательно в том же порядке. другой Таким образом, первая половина каждой строки является дополнением . Тот же вывод применим и ко второй половине каждой строки. В сочетании эти ряды по-прежнему сохраняют полностью хроматическое ощущение и не имеют тенденции усиливать определенные высоты как тональные центры, как это могло бы произойти со свободно объединенными рядами. Например, строка из «Моисей и Арон » Шенберга выше содержит: 0 1 4 5 6 7, это преобразуется в: 0 e 8 7 6 5, добавьте три = 2 3 8 9 t e.
01 4567 : 1st hexachord P0/2nd hexachord I3 23 89te : 2nd hexachord P0/1st hexachord I3 complete chromatic scale
Ретроградно-инверсионная комбинаторность - это отсутствие общих высот между гексахордами ряда и его ретроградно-инверсия.
Бэббит также описал полукомбинаторный ряд и полностью комбинаторный ряд, причем последний представляет собой ряд, который является комбинаторным с любым из его производных и их транспозиций. Полукомбинаторные множества — это множества, гексахорды которых способны образовывать агрегат с транспонированным одним из его основных преобразований (R, I, RI). Есть тринадцать гексахорд, которые являются полукомбинаторными только благодаря инверсии.
(0) 0 1 2 3 4 6 // e t 9 8 7 5 (1) 0 1 2 3 5 7 // e t 9 8 6 4 (2) 0 1 2 3 6 7 // e t 9 8 5 4 (3) 0 1 2 4 5 8 // e t 9 7 6 3 (4) 0 1 2 4 6 8 // e t 9 7 5 3 (5) 0 1 2 5 7 8 // e t 9 6 4 3 (6) 0 1 3 4 6 9 // e t 8 7 5 2 (7) 0 1 3 5 7 9 // e t 8 6 4 2 (8) 0 1 3 5 8 9 // 7 6 4 2 e t (9) 0 1 3 6 7 9 // e t 8 5 4 2 (10) 0 1 4 5 6 8 // 3 2 e t 9 7 (11) 0 2 3 4 6 8 // 1 e t 9 7 5 (12) 0 2 3 5 7 9 // 1 e t 8 6 4
Любой гексахорд, содержащий ноль в своем интервальном векторе, обладает транспозиционной комбинаторностью (другими словами: для достижения комбинаторности гексахорд не может быть транспонирован на интервал, равный содержащейся в нем ноте). Например, есть один гексахорд, который является комбинаторным путем транспозиции (Т6):
(0) 0 1 3 4 5 8 // 6 7 9 t e 2
Ни один из гексахордов не содержит тритонов.


Полностью комбинаторные множества — это множества, гексахорды которых способны образовывать агрегат с транспонированными любыми его основными преобразованиями. Существует шесть исходных наборов или базовых гексахордно-комбинаторных наборов, каждый гексахорд из которых может быть переупорядочен внутри себя:
(A) 0 1 2 3 4 5 // 6 7 8 9 t e (B) 0 2 3 4 5 7 // 6 8 9 t e 1 (C) 0 2 4 5 7 9 // 6 8 t e 1 3 (D) 0 1 2 6 7 8 // 3 4 5 9 t e (E) 0 1 4 5 8 9 // 2 3 6 7 t e (F) 0 2 4 6 8 t // 1 3 5 7 9 e
Примечание: т = 10, е = 11.
Поскольку каждый из первых трех наборов ( A , B и C ) удовлетворяет всем четырем критериям только для одного транспозиционного значения, набор D удовлетворяет им для двух транспозиционных значений, E для трех значений и F для шести транспозиций, Бэббит обозначает эти четыре группы. как полностью комбинаторные гексахорды «первого», «второго», «третьего» и «шестого порядка» соответственно. [13] Обратите внимание, что первый набор, набор «ля», представляет собой первые шесть нот восходящей хроматической гаммы, а последний набор, набор «фа», представляет собой целотоновую гамму. [14]
Комбинаториальность может использоваться для создания совокупности всех двенадцати тонов, хотя этот термин часто относится просто к комбинаторным рядам, изложенным вместе.
Гексахордальная комбинаториальность — понятие в посттональной теории, описывающее сочетание гексахордов, часто используемое применительно к музыке Второй венской школы . В музыке, в которой последовательно используются все двенадцать хроматических тонов (особенно двенадцатитоновая и последовательная музыка ), совокупность (совокупность всех 12 классов высоты звука) может быть разделена на два гексахорда (наборы по 6 тонов). Это разбивает агрегат на две более мелкие части, что упрощает упорядочивание примечаний, переход между строками или агрегатами, а также объединение примечаний и агрегатов.
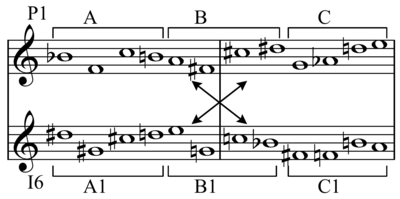
Иногда в особом случае гексахорд можно комбинировать с его перевернутой или транспонированной версией, что затем приводит к совокупности (полный набор из 12 хроматических тонов).
Ряд (B ♭ =0: 0 6 8 5 7 e 4 3 9 t 1 2), используемый Шёнбергом, можно разделить на два гексахорда:
B♭ E F♯ E♭ F A // D C♯ G G♯ B C
Когда вы инвертируете первый гексахорд и транспонируете его, получается следующий гексахорд, перестановка второго гексахорда:
G C♯ B D C G♯ = D C♯ G G♯ B C
Таким образом, когда вы накладываете исходный гексахорд 1 (P0) на транспонированную инверсию гексахорда 1 (в данном случае I9), в результате получается весь набор из 12 тонов. Если вы продолжите остальную часть транспонированного перевернутого ряда (I9) и наложите исходный гексахорд 2, вы снова получите полный набор из 12 хроматических тонов.

Гексахордальная комбинаторность тесно связана с теорией 44 тропов , созданной Йозефом Маттиасом Хауэром в 1921 году, хотя кажется, что Хауэр вообще не оказал никакого влияния на Бэббита. Более того, существует мало доказательств того, что Хауэр обладал обширными знаниями об инверсионных свойствах тропов, по крайней мере, до 1942 года. [17] Однако самые ранние записи о комбинаторных отношениях гексахордов можно найти среди теоретических работ австрийского композитора и теоретика музыки Отмара Штайнбауэра . [а] В начале 1930-х годов он провел тщательное исследование системы тропов, которое задокументировано в неопубликованном машинописном тексте Klang- und Meloslehre (1932). Материалы Штейнбауэра, датированные 1932–1934 гг., содержат исчерпывающие сведения о комбинаторных трихордах, тетрахордах и гексахордах, включая полукомбинаторные и общекомбинаторные множества. Таким образом, они могут быть самыми ранними пластинками в истории музыки. [18] Сборник морфологического материала Штайнбауэра частично стал общедоступным в 1960 году вместе с его сценарием Lehrbuch der Klangreihenkomposition (авторское издание) и был переиздан в 2001 году. [19]
Трихордальная комбинаторность [ править ]
Полностью комбинаторный производный ряд , состоящий из четырех трихорд : P RI R I.
Трихордальная комбинаторность — это способность ряда образовывать агрегаты посредством соединения трихорд. «Трихордальная комбинаторность предполагает одновременное предъявление четырёх рядов в посылках по три штуки». [20] Существование трихордальной комбинаторности или любой другой формы в строке не исключает существования других форм комбинаторности (по крайней мере, тривиальная гексахордальная комбинаторность существует между каждой формой строки и ее ретроградной). Все трихордальные строки обладают трихордальной комбинаторностью.
Примечания [ править ]
- ^ Штайнбауэр (1895–1962) был бывшим учеником Арнольда Шенберга и Йозефа Маттиаса Хауэра. См. статью Штайнбауэра на de.wikipedia.org.
Источники [ править ]
- ↑ Перейти обратно: Перейти обратно: а б с Уиттолл, Арнольд . 2008. Кембриджское введение в сериализм. Кембриджские введения в музыку , с. 272. Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-86341-4 (в твердом переплете) ISBN 978-0-521-68200-8 (пбк).
- ↑ Перейти обратно: Перейти обратно: а б Кристенсен, Томас (2002). Кембриджская история теории западной музыки , [без страниц] . Кембридж. ISBN 9781316025482 .
- ^ Джордж Перл , Серийная композиция и атональность: Введение в музыку Шенберга, Берга и Веберна , четвертое издание, исправленное (Беркли, Лос-Анджелес, Лондон: University of California Press, 1977), 129–131. ISBN 0-520-03395-7
- ^ Питер Вестергаард , «Некоторые проблемы, возникающие в связи с ритмическими процедурами в композиции Милтона Бэббита для двенадцати инструментов », Перспективы новой музыки 4, вып. 1 (осень – зима 1965 г.): 109–118. Цитирование по 114.
- ^ Киелиан-Гилберт, Марианна (1982–83). «Взаимосвязь симметричных наборов высотных классов и метафора полярности Стравинского», Perspectives of New Music 21: 210. JSTOR 832874 .
- ^ Уиттолл, 103
- ^ Уиттолл, 245n8
- ^ Милтон Бэббит , Обзор без названия, Журнал Американского музыковедческого общества 3, вып. 1 (весна 1950 г.): 57–60. Обсуждение комбинаторности находится на стр. 60.
- ^ Мид, Эндрю (2002). «Двенадцатитоновая композиция и музыка Эллиота Картера», Концертная музыка, рок и джаз с 1945 года: очерки и аналитические исследования , стр. 80–81. Элизабет Вест Марвин, Ричард Германн; ред. Университет Рочестера. ISBN 9781580460965 .
- ^ Харви, Джонатан (1975). Музыка Штокхаузена , стр. 56–58. ISBN 0-520-02311-0 .
- ^ Дэвид Левин , «Re: Интервальные отношения между двумя сборниками заметок». Журнал теории музыки 3, вып. 2 (ноябрь 1959 г.): 298–301. п. 300.
- ↑ Перейти обратно: Перейти обратно: а б Ван ден Тоорн, Питер К. (1996). Музыка, политика и Академия , стр. 128–129. ISBN 0-520-20116-7 .
- ^ Джон Ран , Основная атональная теория , Музыкальная серия Longman (Нью-Йорк и Лондон: Longman, 1980): 118.
- ^ Кастанеда, Рэмси (март 2016 г.). «Общекомбинаторные гексахорды» . Проверено 1 июня 2016 г.
- ^ Леу, Тон де (2005). Музыка двадцатого века: исследование ее элементов и структуры . Перевод Стивена Тейлора. Амстердам: Издательство Амстердамского университета. стр. 155–157. ISBN 90-5356-765-8 . Перевод музыки двадцатого века: исследование ее элементов и структуры . Утрехт: Остхук, 1964. Третье впечатление, Утрехт: Бон, Шелтема и Холкема, 1977. ISBN 90-313-0244-9 .
- ^ Леув 2005 , стр. 154–155.
- ^ Дидерихс, Иоахим. Федоров, Николай. Швигер, Йоханнес (ред.). 2007. Йозеф Матиас Хауэр: Сочинения, манифесты, документы 428–440. Вена: Издательство Lafite
- ^ Седиви, Доминик. 2011. Серийная композиция и тональность. Введение в музыку Хауэра и Штайнбауэра , с. 70. Вена: издание моно/монохром. ISBN 978-3-902796-03-5 . Седиви, Доминик. 2012. Тропические технологии. Их применение и возможности , 258–264. Зальцбургский булл 5. Вюрцбург: Кенигсхаузен и Нойманн. ISBN 978-3-8260-4682-7
- ^ Нойманн, Гельмут. 2001. Теория композиции звуковых рядов по Отмару Штайнбауэру (1895–1962) , 184–187, 201–213, 234–236. 2 тома Франкфурт и др.: Питер Ланг.
- ^ Моррис, Роберт (1991). Заметки по теории атональной музыки , с. 82. Музыка Лягушачьего Пика. ASIN B0006DHW9I [ISBN не указан].