Двенадцатитоновая техника

Техника двенадцати тонов , также известная как додекафония , двенадцатитоновый сериализм и (в британском использовании) композиция из двенадцати нот — это метод музыкальной композиции, впервые разработанный австрийским композитором Йозефом Матиасом Хауэром . [ не проверено в теле ] опубликовавший в 1919 году свой «Закон двенадцати тонов». В 1923 году Арнольд Шенберг (1874–1951) разработал собственную, более известную версию 12-тоновой техники, которая стала ассоциироваться с композиторами « Второй венской школы », которые были основными пользователями этой техники в первые десятилетия ее существования. Этот метод представляет собой средство обеспечения того, чтобы все 12 нот хроматической гаммы звучали в музыкальном произведении так же часто, как друг друга, при этом не допуская выделения какой-либо одной ноты. [3] посредством использования рядов тонов , упорядочения 12 классов высоты тона . Таким образом, всем 12 нотам придается более или менее равное значение, и музыка избегает тональности . Со временем популярность этой техники значительно возросла и в конечном итоге она оказала большое влияние на композиторов 20-го века. Многие важные композиторы, которые изначально не поддерживали эту технику или активно выступали против нее, такие как Аарон Копленд и Игорь Стравинский , [ нужны разъяснения ] в конце концов применили это в своей музыке.
Сам Шенберг описал эту систему как «Метод сочинения двенадцати тонов, связанных только друг с другом». [4] Это обычно считается формой сериализма .
Земляк Шенберга и современник Хауэр также разработал аналогичную систему с использованием неупорядоченных гексахордов или тропов - независимо от разработки Шенбергом техники двенадцати тонов. Другие композиторы систематически использовали хроматическую гамму, но метод Шёнберга считается наиболее исторически и эстетически значимым. [5]
История использования
[ редактировать ]Хотя в большинстве источников говорится, что он был изобретен австрийским композитором Арнольдом Шенбергом в 1921 году и впервые описан в частном порядке своим коллегам в 1923 году, на самом деле Йозеф Матиас Хауэр опубликовал свой «закон двенадцати тонов» в 1919 году, требуя, чтобы все двенадцать хроматических нот звучали раньше, чем любая нота повторяется. [8] [ не удалось пройти проверку ] Метод использовался в течение следующих двадцати лет почти исключительно композиторами Второй венской школы — Альбаном Бергом , Антоном Веберном и самим Шенбергом. Однако еще одним важным композитором этого периода была Элизабет Лютиенс , написавшая более 50 произведений серийным методом. [9]
Технике двенадцати тонов предшествовали «свободные» атональные пьесы 1908–1923 годов, которые, хотя и «свободные», часто имеют в качестве «интегративного элемента ... минутную интервальную ячейку », которая помимо расширения может трансформироваться, как при помощи тона. строка, и в которой отдельные примечания могут «функционировать как основные элементы, позволяя перекрываться утверждениями базовой ячейки или связывать две или более базовых ячеек». [10] Двенадцатитоновой технике также предшествовала «недодекафоническая серийная композиция», использовавшаяся самостоятельно в творчестве Александра Скрябина , Игоря Стравинского , Белы Бартока , Карла Рагглса и других. [11] Оливер Нейбор утверждает, что Барток был «первым композитором, который сознательно использовал группу из двенадцати нот для структурных целей» в 1908 году с третьей из своих четырнадцати вещиц. [12] «По сути, Шенберг и Хауэр систематизировали и определили для своих собственных додекафонических целей распространенную техническую особенность «современной» музыкальной практики - остинато ». [11] Кроме того, Джон Ковач утверждает, что строгое различие между ними, подчеркиваемое авторами, в том числе Перлом, преувеличено:
Различие, которое часто проводят между Хауэром и школой Шёнберга (что музыка первого основана на неупорядоченных гексахордах, а музыка второго — на упорядоченной серии), неверно: хотя он и писал пьесы, которые можно было бы рассматривать как «тропические пьесы», во многом Двенадцатитоновая музыка Хауэра представляет собой упорядоченную серию. [13]
«Строгая упорядоченность» Второй венской школы, напротив, «неизбежно смягчалась практическими соображениями: они действовали на основе взаимодействия упорядоченных и неупорядоченных наборов звуков». [14]
Рудольф Рети , один из первых сторонников, говорит: «Замена одной структурной силы (тональности) другой (повышенное тематическое единство) действительно является фундаментальной идеей, лежащей в основе техники двенадцати тонов», утверждая, что она возникла из-за разочарования Шенберга свободной атональностью. [15] [ нужна страница ] обеспечивая «позитивную предпосылку» атональности. [3] В революционной пьесе Хауэра «Номос» , соч. 19 (1919) он использовал двенадцатитоновые секции для обозначения крупных формальных подразделений, например, с первыми пятью утверждениями одной и той же двенадцатитоновой серии, изложенными в группах по пять нот, образующих двенадцать пятинотных фраз. [14]
Феликс Хунер противопоставил более математическую концепцию Хауэра более музыкальному подходу Шенберга. [16] Идея Шенберга при разработке этой техники заключалась в том, чтобы «заменить структурные различия, которые раньше обеспечивались тональными гармониями ». [4] Таким образом, двенадцатитоновая музыка обычно атональна и рассматривает каждый из 12 полутонов хроматической гаммы с одинаковой важностью, в отличие от более ранней классической музыки, которая считала некоторые ноты более важными, чем другие (особенно тонику и доминантную ноту). ).
Техника стала широко использоваться в пятидесятые годы, ее подхватили такие композиторы, как Милтон Бэббит , Лучано Берио , Пьер Булез , Луиджи Даллапиккола , Эрнст Кренек , Риккардо Малипьеро и, после смерти Шенберга, Игорь Стравинский . Некоторые из этих композиторов расширили эту технику, чтобы управлять другими аспектами, помимо высоты нот (такими как продолжительность, метод атаки и т. д.), создавая таким образом последовательную музыку . Некоторые даже подвергали серийному процессу все элементы музыки.
Чарльз Вуоринен сказал в интервью 1962 года, что, хотя «большинство европейцев говорят, что они «вышли за пределы» и «исчерпали» двенадцатитоновую систему», в Америке «двенадцатитоновая система была тщательно изучена и обобщена в здание более впечатляющее, чем любое известное до сих пор». [17]
Американский композитор Скотт Брэдли , наиболее известный своими партитурами к таким произведениям, как «Том и Джерри» и «Друпи Дог» , использовал в своей работе технику 12 тонов. Брэдли описал свое использование так:
Двенадцатитоновая система обеспечивает «неземное» развитие событий, столь необходимое для описания фантастических и невероятных ситуаций, которые содержатся в современных мультфильмах. [18]
Пример использования Брэдли этой техники для передачи нарастающего напряжения можно найти в короткометражке Тома и Джерри « Надеваем собаку » 1944 года. В сцене, где мышь в собачьей маске бежит через двор с собаками «в маскировка», хроматическая гамма представляет как движения мыши, так и приближение подозрительной собаки, зеркально отраженной на октавы ниже. [19] Помимо работы над партитурами для мультфильмов, Брэдли также сочинял тональные стихотворения , которые исполнялись на концертах в Калифорнии. [20]
Рок-гитарист Рон Джарзомбек использовал двенадцатитоновую систему для написания Blotted Science The расширенной пьесы Animation of Entomology . Он поместил ноты в часы и переставил их для использования рядом или последовательно. Он назвал свой метод «Двенадцать тонов во фрагментированных рядах». [21]
Тоновый ряд
[ редактировать ]Основой двенадцатитоновой техники является тональный ряд — упорядоченное расположение двенадцати нот хроматической гаммы (двенадцать равных темперированных классов высоты звука ). Есть четыре постулата или предварительных условия этой техники, которые применимы к ряду (также называемому набором или серией ), на котором основано произведение или раздел: [22]
- Ряд представляет собой определенный порядок всех двенадцати нот хроматической гаммы (без учета расположения октав ).
- Ни одна нота не повторяется внутри строки.
- Строка может быть подвергнута интервал сохраняющим преобразованиям, , то есть она может появиться в инверсии (обозначенной I), ретроградной (R) или ретроградной инверсии (RI) в дополнение к своей «исходной» или простой форме (P). .
- Ряд в любом из четырех преобразований может начинаться на любой ступени хроматической гаммы; другими словами, его можно свободно транспонировать . (Транспозиция является преобразованием, сохраняющим интервалы, технически это уже покрывается цифрой 3.) Транспозиции обозначаются целым числом от 0 до 11, обозначающим количество полутонов: таким образом, если исходная форма строки обозначается P 0 , то P 1 обозначает его транспозицию вверх на один полутон (аналогично I 1 - транспозиция вверх перевернутой формы, R 1 - ретроградной формы, RI 1 - ретроградно-перевернутой формы).
(В системе Хауэра постулат 3 неприменим.) [2]
Конкретное преобразование (простое, инверсное, ретроградное, ретроградно-инверсное) вместе с выбором транспозиционного уровня называется формой множества или формой строки . Таким образом, каждая строка имеет до 48 различных форм строк. (Некоторые строки имеют меньшее количество из-за симметрии ; см. разделы о производных строках и инвариантности ниже.)
Пример
[ редактировать ]Предположим, что простая форма строки имеет следующий вид:
Тогда ретроградность является простой формой в обратном порядке:
Инверсия - это простая форма с интервалами перевернутыми (так что восходящая второстепенная терция становится нисходящей второстепенной терцией или, что то же самое, восходящей мажорной шестой ):
А ретроградная инверсия – это перевернутый ряд в ретроградном порядке:
P, R, I и RI могут начинаться с любой из двенадцати нот хроматической гаммы , что означает, что можно использовать 47 перестановок начального ряда тонов, что дает максимум 48 возможных рядов тонов. Однако не все простые ряды дадут такое большое количество вариаций, поскольку транспонированные преобразования могут быть идентичны друг другу. Это известно как инвариантность . Простым случаем является восходящая хроматическая гамма, ретроградная инверсия которой идентична первичной форме, а ретроградная идентична инверсии (таким образом, доступны только 24 формы этого тонового ряда).

В приведенном выше примере, как это обычно бывает, ретроградная инверсия содержит три точки, в которых последовательность двух шагов идентична первому ряду. Таким образом, порождающая сила даже самых фундаментальных преобразований одновременно непредсказуема и неизбежна. Такая внутренняя последовательность может стимулировать развитие мотивации.
Применение в составе
[ редактировать ]Обратите внимание, что правила 1–4 выше применяются к построению самой строки, а не к интерпретации строки в композиции. (Так, например, постулат 2 не означает, вопреки распространённому мнению, что ни одна нота в двенадцатитоновом произведении не может повторяться до тех пор, пока не будут озвучены все двенадцать.) Хотя ряд может быть выражен буквально на поверхности как тематический материал В этом нет необходимости, и вместо этого он может управлять структурой тональности произведения более абстрактными способами. Даже когда техника применяется самым буквальным образом, когда произведение состоит из последовательности высказываний строковой формы, эти высказывания могут появляться последовательно, одновременно или могут перекрываться, порождая гармонию .

Длительность, динамика и другие аспекты музыки, кроме высоты звука, могут свободно выбираться композитором, а также не существует общих правил относительно того, какие ряды тонов следует использовать в какое время (кроме того, все они выводятся из простого ряда, как уже было сказано выше). объяснил). Однако отдельные композиторы создали более подробные системы, в которых подобные вопросы также регулируются систематическими правилами (см. Сериализм ).
Топография
[ редактировать ]Аналитик Кэтрин Бейли использовала термин «топография» для описания особого способа расположения нот ряда в своей работе над додекафонической музыкой Веберна. Она выделяет два типа топографии в музыке Веберна: блочную топографию и линейную топографию.
Первый, который она считает «самым простым», определяется следующим образом: «ряды устанавливаются один за другим, при этом все ноты звучат в порядке, предписанном этой последовательностью рядов, независимо от текстуры». Последний более сложен: музыкальная текстура «является продуктом нескольких рядов, развивающихся одновременно в таком же количестве голосов» (обратите внимание, что эти «голоса» не обязательно ограничиваются отдельными инструментами и, следовательно, прорезают музыкальную текстуру, действуя скорее как фоновая структура). [24]
Элизии, цепочки и циклы
[ редактировать ]Последовательные ряды могут быть соединены посредством исключения - термина, описывающего «перекрытие двух рядов, которые происходят последовательно, так что одна или несколько нот в месте соединения являются общими (играются только один раз для обслуживания обоих рядов)». [25] Когда это исключение включает две или более нот, оно создает цепочку строк; [26] когда несколько строк соединены одним и тем же элиминированием (обычно идентифицируемым как одно и то же в терминах классов множеств), это создает цикл цепочки строк, который, следовательно, обеспечивает метод организации групп строк. [27]
Свойства преобразований
[ редактировать ]Тональный ряд, выбранный в качестве основы произведения, называется простым рядом (П). В нетранспонированном виде он обозначается как P 0 . Учитывая двенадцать классов высоты хроматической гаммы, существует 12 факториалов. [28] (479,001,600 [14] ) тоновых рядов, хотя это намного больше, чем количество уникальных тональных рядов (с учётом преобразований). Существует 9 985 920 классов двенадцатитоновых рядов с точностью до эквивалентности (где два ряда эквивалентны, если один является преобразованием другого). [29]
Внешний вид P можно преобразовать из оригинала тремя основными способами:
- транспонирование вверх или вниз, давая P χ .
- меняя порядок звуков на обратный, давая ретроградный (R)
- поворачивая направление каждого интервала в противоположное, создавая инверсию (I).
Различные преобразования можно комбинировать. Они порождают набор-комплекс из сорока восьми форм множества, 12 транспозиций четырех основных форм: P, R, I, RI. Сочетание ретроградного и инверсионного преобразований известно как ретроградная инверсия ( RI ).
РИ это: РИ П, Р я, и я Р. Р это: Р П, РИ Я, и я из РИ. Я: Я из П, РИ Р, и Р РИ. П это: Р Р, я из меня, и РИ РИ.
таким образом, каждая ячейка в следующей таблице содержит результат преобразований, группу из четырех элементов , в заголовках строк и столбцов:
П: РИ: Р: Я: РИ: П я Р Р: я П РИ Я: Р РИ П
Однако есть лишь несколько чисел, на которые можно умножить ряд и все равно получить двенадцать тонов. (Умножение в любом случае не сохраняет интервал.)
Вывод
[ редактировать ]Деривация — это преобразование сегментов полной хроматики, менее 12 классов высоты звука, в полный набор, чаще всего с использованием трихордов, тетрахордов и гексахордов. может Производный набор быть создан путем выбора соответствующих преобразований любой трихорды, кроме 0,3,6, уменьшенной триады. [ нужна ссылка ] . Производный набор также может быть создан из любого тетрахорда , исключающего класс интервалов 4, большую треть , между любыми двумя элементами. Противоположный вариант, секционирование , использует методы для создания сегментов из наборов, чаще всего посредством регистрационных различий .
Комбинаторность
[ редактировать ]Комбинаториальность - это побочный эффект производных строк, в которых различные сегменты или наборы объединяются таким образом, что содержание класса высоты тона результата соответствует определенным критериям, обычно это комбинация гексахордов, которые завершают полную хроматику.
Инвариантность
[ редактировать ]Инвариантные образования также являются побочным эффектом производных строк, когда сегмент набора остается аналогичным или неизменным при преобразовании. Они могут использоваться в качестве «поворотов» между заданными формами, что иногда использовали Антон Веберн и Арнольд Шенберг . [31]
Инвариантность определяется как «свойства набора, которые сохраняются при [любой данной] операции, а также те отношения между набором и таким операционно преобразованным набором, которые присущи операции». [32] определение очень близкое к определению математической инвариантности . Джордж Перл описывает их использование как «повороты» или нетональные способы подчеркнуть определенные высоты звука . Инвариантные строки также являются комбинаторными и производными .
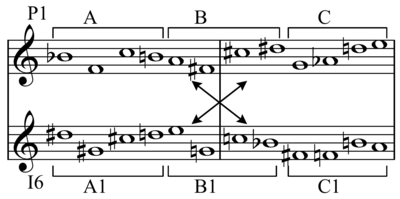
Поперечная перегородка
[ редактировать ]
Поперечное разделение - это часто монофонический или гомофонный метод, который «организует тональные классы агрегата (или ряда) в прямоугольную конструкцию», в которой вертикальные столбцы (гармонии) прямоугольника получаются из соседних сегментов строка и горизонтальные столбцы (мелодии) не являются (и, следовательно, могут содержать несмежности). [34]
Например, расположение всех возможных «четных» перекрестных разделов выглядит следующим образом: [35]
6 2 4 3 3 4 2 6 ** *** **** ****** ** *** **** ****** ** *** **** ** *** ** **
Одна возможная реализация из многих для порядковых номеров 3 4 перекрестное разделение и один из его вариантов: [35]
0 3 6 9 0 5 6 e 1 4 7 t 2 3 7 t 2 5 8 e 1 4 8 9
Таким образом, если бы ряд тонов был 0 e 7 4 2 9 3 8 t 1 5 6, поперечные разбиения сверху были бы:
0 4 3 1 0 9 3 6 e 2 8 5 7 4 8 5 7 9 t 6 e 2 t 1
Поперечные перегородки используются в сочинении Шёнберга. 33a Klavierstück , а также Берга , но Даллапикола использовал их больше, чем любой другой композитор. [36]
Другой
[ редактировать ]На практике «правила» двенадцатитоновой техники неоднократно нарушались и нарушались, не в последнюю очередь самим Шенбергом. Например, в некоторых произведениях можно услышать одновременное развитие двух или более тоновых рядов или могут быть части композиции, написанные свободно, вообще без обращения к двенадцатитоновой технике. Ответвления или вариации могут создавать музыку, в которой:
- полная хроматика используется и постоянно циркулирует, но приемы перестановки игнорируются
- перестановочные приемы используются, но не на полной хроматике.
Кроме того, некоторые композиторы, в том числе Стравинский, использовали циклическую перестановку или вращение, когда строка берется по порядку, но с использованием другой начальной ноты. Стравинский также предпочитал инверсно-ретроградную , а не ретроградно-инвертированную форму, рассматривая первую как композиционно преобладающую, «нетранспонированную» форму. [37]
Хотя двенадцатитоновая музыка обычно атональна, она не обязательно должна быть - например, некоторые произведения Берга содержат тональные элементы.
Одно из самых известных двенадцатинотных произведений — «Вариации для оркестра» Арнольда Шенберга . «Тихо» в » Леонарда Бернштейна высмеивает « Кандиде этот метод, используя его в песне о скуке, а Бенджамин Бриттен использовал двенадцатитоновый ряд — «tema seriese con fuga» — в своей «Академической кантате: Кармен Базилиенсе» (1959) . ) как эмблема академизма. [38]
Зрелая практика Шёнберга
[ редактировать ]Десять особенностей зрелой двенадцатитоновой практики Шенберга характерны, взаимозависимы и интерактивны: [39]
- Гексахордальная инверсионная комбинаторность
- Агрегаты
- линейного набора Представление
- Разделение
- Изоморфное разбиение
- Инварианты
- Шестихордальные уровни
- Гармония , «согласованная со свойствами референтного набора и вытекающая из них»
- Метр , установленный через «высотно-относительные характеристики».
- Многомерные презентации наборов.
См. также
[ редактировать ]- Список додекафонических и серийных композиций
- Всеинтервальный двенадцатитоновый ряд
- Всеинтервальный тетрахорд
- Полностью трихордовый гексахорд
- Интервал шага
- Список рядов и серий тонов
Ссылки
[ редактировать ]Примечания
[ редактировать ]- ^ Уиттолл 2008, 26.
- ^ Перейти обратно: а б Перл 1991, 145.
- ^ Перейти обратно: а б Перл 1977, 2.
- ^ Перейти обратно: а б Шенберг 1975, 218.
- ^ Уиттолл 2008, 25.
- ^ Лев 2005, 149.
- ^ Лео 2005, 155–157.
- ^ Шенберг 1975, 213.
- ^ «Элизабет Лютьенс» . Музыкальные времена . 124 (1684): 378–378. 1983. ISSN 0027-4666 .
- ^ Перл 1977, 9–10.
- ^ Перейти обратно: а б Перл 1977, 37.
- ^ Сосед 1955, 53.
- ^ Джон Ковач, цитируется в Whittall 2008, 24.
- ^ Перейти обратно: а б с Уиттолл 2008, 24.
- ^ Редкий 1958 г.
- ^ Кроуфорд и Хунер 1996 , 28.
- ^ Чейз 1987, 587.
- ^ Йоуп (7 января 2017 г.). «Тралфаз: Композитор мультфильмов Скотт Брэдли» .
- ^ Голдмарк, Дэниел (2007). Мелодии для мультфильмов: музыка и голливудский мультфильм . Университет Калифорнии Пресс. п. 71. ИСБН 978-0-520-25311-7 .
- ^ Скотт Брэдли на IMDb
- ^ Мастейн, Дэйв (2 ноября 2011 г.). «Рон Джарзомбек из Blotted Science: Интервью Twelve-tone Metalsucks» . Металл-отстой . Проверено 19 января 2021 г.
- ^ Перл 1977, 3.
- ^ Уиттолл 2008, 52.
- ^ Бейли, Кэтрин (2006). Двенадцатинотная музыка Антона Веберна: старые формы в новом языке . Музыка в ХХ веке (Цифровая печать, 1-я пбк. Версия под ред.). Кембридж [Англия] Нью-Йорк: Издательство Кембриджского университета. п. 31. ISBN 978-0-521-39088-0 .
- ^ Бейли, Кэтрин (2006). Двенадцатинотная музыка Антона Веберна: старые формы в новом языке . Музыка в ХХ веке (Цифровая печать, 1-я пбк. Версия под ред.). Кембридж [Англия] Нью-Йорк: Издательство Кембриджского университета. п. 449. ИСБН 978-0-521-39088-0 .
- ^ Мозли, Брайан (1 сентября 2019 г.). «Цепочки трансформаций, ассоциативные области и принцип формы двенадцатитоновой музыки Антона Веберна» . Теория музыки Спектр . 41 (2): 218–243. дои : 10.1093/mts/mtz010 . ISSN 0195-6167 .
- ^ Мозли, Брайан (2018). «Циклы в поздней музыке Веберна» . Журнал теории музыки . 62 (2): 165–204. дои : 10.1215/00222909-7127658 . ISSN 0022-2909 . S2CID 171497028 .
- ^ Лой 2007, 310.
- ^ Бенсон 2007, 348.
- ^ Хаймо 1990, 27.
- ^ Перл 1977, 91–93.
- ^ Бэббит 1960, 249–250.
- ^ Хаймо 1990, 13.
- ^ Аллегант 2010, 20.
- ^ Перейти обратно: а б Аллегант 2010, 21.
- ^ Аллегант 2010, 22, 24.
- ^ Шпионы 1965, 118.
- ^ Бретт 2007.
- ^ Хаймо 1990, 41.
Источники
[ редактировать ]- Алегант, Брайан. 2010. Двенадцатитоновая музыка Луиджи Даллапикколы . Исследования Истмана в области музыки 76. Рочестер, Нью-Йорк: Университет Рочестера Press. ISBN 978-1-58046-325-6 .
- Бэббит, Милтон . 1960. «Двенадцатитоновые инварианты как детерминанты композиции». Музыкальный ежеквартальный журнал 46, вып. 2, специальный выпуск: Проблемы современной музыки: Принстонский семинар по углубленным музыкальным исследованиям (апрель): 246–259. дои : 10.1093/mq/XLVI.2.246 . JSTOR 740374 (требуется подписка) .
- Бэббит, Милтон. 1961. "Структура набора как композиционный детерминант". Журнал теории музыки 5, вып. 1 (Весна): 72–94. JSTOR 842871 (требуется подписка) .
- Бенсон, Дэйв. 2007 Музыка: математическое предложение . Кембридж и Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-85387-3 .
- Бретт, Филип. «Бриттен, Бенджамин». Grove Music Online изд. Л. Мэйси (по состоянию на 8 января 2007 г.)
- Чейз, Гилберт . 1987. Музыка Америки: от паломников до наших дней , переработанное третье издание. Музыка в американской жизни. Урбана: Издательство Университета Иллинойса. ISBN 0-252-00454-X (ткань); ISBN 0-252-06275-2 (pbk).
- Кроуфорд, Кэролайн и Феликс Хунер . 1996. Феликс Хунер: Путешествие скрипача от венского квартета Колиш до симфонического и оперного оркестров Сан-Франциско , вступление. Том Хеймберг. Региональный офис устной истории , Библиотека Бэнкрофта . Беркли: Калифорнийский университет.
- Хаймо, Итан. 1990. Серийная одиссея Шёнберга: эволюция его двенадцатитонового метода, 1914–1928 . Оксфорд [Англия] Clarendon Press; Нью-Йорк: Издательство Оксфордского университета. ISBN 0-19-315260-6 .
- Хилл, Ричард С. 1936. «Тональные ряды Шенберга и тональная система будущего». Музыкальный ежеквартальный журнал 22, вып. 1 (январь): 14–37. дои : 10.1093/mq/XXII.1.14 . JSTOR 739013 (требуется подписка) .
- Лански, Пол ; Джордж Перл и Дэйв Хедлам. 2001. «Двенадцатинотная композиция». Словарь музыки и музыкантов New Grove , второе издание, под редакцией Стэнли Сэди и Джона Тиррелла . Лондон: Макмиллан.
- Леу, Тон де . 2005. Музыка двадцатого века: исследование ее элементов и структуры , перевод с голландского Стивена Тейлора. Амстердам: Издательство Амстердамского университета. ISBN 90-5356-765-8 . Перевод музыки двадцатого века: исследование ее элементов и структуры . Утрехт: Остхук, 1964. Третье впечатление, Утрехт: Бон, Шелтема и Холкема, 1977. ISBN 90-313-0244-9 .
- Лой, Д. Гарет, 2007. Музыкатика: математические основы музыки , Vol. 1. Кембридж, Массачусетс и Лондон: MIT Press. ISBN 978-0-262-12282-5 .
- Сосед Оливер . 1954. «Эволюция двенадцатинотной музыки». Труды Королевской музыкальной ассоциации , том 81, выпуск 1: 49–61. дои : 10.1093/jrma/81.1.49
- Перл, Джордж . 1977. Серийная композиция и атональность: введение в музыку Шенберга, Берга и Веберна , четвертое издание, исправленное. Беркли, Лос-Анджелес и Лондон: Калифорнийский университет Press. ISBN 0-520-03395-7
- Перл, Джордж. 1991. Серийная композиция и атональность: введение в музыку Шенберга, Берга и Веберна , шестое издание, исправленное. Беркли: Издательство Калифорнийского университета. ISBN 978-0-520-07430-9 .
- Рети, Рудольф . 1958. Тональность, атональность, пантональность: исследование некоторых тенденций в музыке двадцатого века . Вестпорт, Коннектикут: Greenwood Press. ISBN 0-313-20478-0 .
- Руфер, Йозеф . 1954. Композиция с двенадцатью нотами, связанными только друг с другом , в переводе Хамфри Сирла . Нью-Йорк: Компания Macmillan. (Оригинальное немецкое издание, 1952 г.)
- Шенберг, Арнольд . 1975. Стиль и идея , под редакцией Леонарда Штейна с переводами Лео Блэка. Беркли и Лос-Анджелес: Издательство Калифорнийского университета. ISBN 0-520-05294-3 .
- 207–208 «Двенадцатитоновая композиция (1923)»
- 214–245 «Композиция с двенадцатью тонами (1) (1941)»
- 245–249 «Композиция с двенадцатью тонами (2) (ок. 1948)»
- Соломон, Ларри. 1973. «Новые симметричные преобразования». Перспективы новой музыки 11, вып. 2 (Весна – Лето): 257–264. JSTOR 832323 (требуется подписка) .
- Шпионы, Клаудио . Стравинского 1965. "Заметки об Аврааме и Исааке ". Перспективы новой музыки 3, вып. 2 (Весна – Лето): 104–126. JSTOR 832508 (требуется подписка) .
- Уиттолл, Арнольд . 2008. Кембриджское введение в сериализм . Кембриджские введения в музыку. Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-86341-4 (ткань) ISBN 978-0-521-68200-8 (пбк).
Дальнейшее чтение
[ редактировать ]- Ковач, Джон. 1992. "Цвельфтоншпиль Йозефа Маттиаса Хауэра". Журнал теории музыки 36, вып. 1 (Весна): 149–84. JSTOR 843913 (требуется подписка) .
- Ковач, Джон. 2000. «Поэтика музыки Шенберга, метод двенадцати тонов и музыкальная идея». В книге «Шенберг и слова: годы модернизма » под редакцией Рассела А. Бермана и Шарлотты М. Кросс, Нью-Йорк: Гарланд. ISBN 0-8153-2830-3
- Ковач, Джон. 2002, «Теория двенадцати тонов». В Кембриджской истории теории западной музыки под редакцией Томаса Кристенсена, 603–627. Кембридж: Издательство Кембриджского университета. ISBN 0-521-62371-5 .
- Кренек, Эрнст . 1953. «Приходит ли в упадок двенадцатитоновая техника?» Музыкальный ежеквартальный журнал 39, № 4 (октябрь): 513–527.
- Шедивый, Доминик. 2011. Серийная композиция и тональность. Введение в музыку Хауэра и Штайнбауэра под редакцией Гюнтера Фризингера, Гельмута Ноймана и Доминика Шедивы. Вена: издание моно. ISBN 3-902796-03-0
- Слоан, Сьюзан Л. 1989. « Архивный экспонат: додекафонические устройства Шёнберга ». Журнал Института Арнольда Шенберга 12, вып. 2 (ноябрь): 202–205.
- Старр, Дэниел. 1978. «Множества, инвариантность и разделы». Журнал теории музыки 22, вып. 1 (Весна): 1–42. JSTOR 843626 (требуется подписка) .
- Вуоринен, Чарльз . 1979. Простая композиция . Нью-Йорк: Лонгман. ISBN 0-582-28059-1 . Перепечатано в 1991 году, Нью-Йорк: CF Peters. ISBN 0-938856-06-5 .
Внешние ссылки
[ редактировать ]- Двенадцатитоновый квадрат для поиска всех комбинаций последовательности из 12 тонов.
- Новые трансформации: за пределами P, I, R и RI Ларри Соломон
- Javascript двенадцатитональный матричный калькулятор и анализатор тоновых рядов
- Генератор матриц с сайта musictheory.net Риччи Адамса
- «Техника двенадцати тонов», краткий справочник Дэна Романа
- Двенадцать тонов музыканта-математика Ви Харта на YouTube
- Додекафонические узлы и топология слов Франка Енджеевского
- База данных по тональным рядам и тропам