Интерьер (топология)

Точка x является внутренней точкой S . Точка y находится на границе S .

В математике , особенно в топологии ,внутренность ​ подмножества ​ S топологического пространства X есть объединение всех S открытых , в X. подмножеств находящаяся внутри S, внутренней точкой S. является Точка ,

Внутренность S является дополнением замыкания ​ дополнения S . В этом смысле внутреннее и закрытое — понятия двойственные .

Внешность является множества S дополнением замыкания S ; оно состоит из точек, не принадлежащих ни множеству, ни его границе .Внутренняя часть, граница и внешняя часть подмножества вместе делят все пространство на три блока (или меньше, если один или несколько из них пусты ).

Внутренняя и внешняя часть замкнутой кривой — это немного другая концепция; см. теорему Жордана о кривой .

Определения

Внутренняя точка

Если $S$ является подмножеством евклидова пространства , то $x$ является внутренней точкой $S$ если существует открытый шар с центром в $x$ который полностью содержится в $S.$(Это проиллюстрировано во вступительной части этой статьи.)

Это определение обобщается на любое подмножество $S$ метрического пространства $X$ с метрикой $d$: $x$ является внутренней точкой $S$ если существует действительное число $r>0,$ такой, что $y$ находится в $S$ всякий раз, когда расстояние $d(x,y)<r.$

Это определение обобщается на топологические пространства , заменяя «открытый шар» на « открытое множество ».Если $S$ является подмножеством топологического пространства $X$ затем $x$ является внутренней точкой $S$ в $X$ если $x$ содержится в открытом подмножестве $X$ который полностью содержится в $S.$(Эквивалентно, $x$ является внутренней точкой $S$ если $S$ это район ​ $x.$)

Интерьер набора

Интерьер ​ подмножества $S$ топологического пространства $X,$ обозначается $\operatorname {int} _{X}S$ или $\operatorname {int} S$ или $S^{\circ },$ может быть определен любым из следующих эквивалентных способов:

1. $\operatorname {int} S$ является крупнейшим открытым подмножеством $X$ содержится в $S.$
2. $\operatorname {int} S$ является объединением всех открытых множеств $X$ содержится в $S.$
3. $\operatorname {int} S$ множество всех внутренних точек $S.$

Если пространство $X$ понимается из контекста, тогда более короткая запись $\operatorname {int} S$ обычно предпочитают $\operatorname {int} _{X}S.$

Примеры

$a$ является внутренней точкой $M$ потому что существует ε-окрестность a, которая является подмножеством $M.$

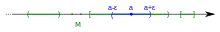
• В любом пространстве внутренняя часть пустого множества — это пустое множество.
• В любом пространстве $X,$ если $S\subseteq X,$ затем $\operatorname {int} S\subseteq S.$
• Если $X$ это настоящая линия $\mathbb {R}$ (со стандартной топологией), то $\operatorname {int} ([0,1])=(0,1)$ тогда как внутренняя часть набора $\mathbb {Q}$ рациональных чисел пусто: $\operatorname {int} \mathbb {Q} =\varnothing$
• Если $X$ это сложная плоскость $\mathbb {C} ,$ затем $\operatorname {int} (\{z\in \mathbb {C} :|z|\leq 1\})=\{z\in \mathbb {C} :|z|<1\}.$
• В любом евклидовом пространстве внутренность любого конечного множества является пустым множеством.

На множестве действительных чисел можно поставить и другие топологии, кроме стандартной:

• Если $X$ это реальные цифры $\mathbb {R}$ с топологией нижнего предела , то $\operatorname {int} ([0,1])=[0,1).$
• Если рассматривать $\mathbb {R}$ топология, в которой каждое множество открыто , то $\operatorname {int} ([0,1])=[0,1].$
• Если рассматривать $\mathbb {R}$ топология, в которой единственными открытыми множествами являются пустое множество и $\mathbb {R}$ сам, тогда $\operatorname {int} ([0,1])$ пустое множество.

Эти примеры показывают, что внутренняя часть множества зависит от топологии лежащего в его основе пространства.Последние два примера являются частными случаями следующего.

• В любом дискретном пространстве , поскольку каждое множество открыто, каждое множество равно своей внутренней части.
• В любом недискретном пространстве $X,$ поскольку единственными открытыми множествами являются пустое множество и $X$ сам, $\operatorname {int} X=X$ и для каждого правильного подмножества $S$ из $X,$ $\operatorname {int} S$ пустое множество.

Характеристики

Позволять $X$ быть топологическим пространством и пусть $S$ и $T$ быть подмножествами $X.$

• $\operatorname {int} S$ открыт ​ в $X.$
• Если $T$ открыт в $X$ затем $T\subseteq S$ тогда и только тогда, когда $T\subseteq \operatorname {int} S.$
• $\operatorname {int} S$ является открытым подмножеством $S$ когда $S$ задана топология подпространства .
• $S$ является открытым подмножеством $X$ тогда и только тогда, когда $\operatorname {int} S=S.$
• Интенсив : $\operatorname {int} S\subseteq S.$
• Идемпотентность : $\operatorname {int} (\operatorname {int} S)=\operatorname {int} S.$
• Сохраняет / распределяет по двоичному пересечению : $\operatorname {int} (S\cap T)=(\operatorname {int} S)\cap (\operatorname {int} T).$
  • Однако внутренний оператор не распределяет по объединениям, поскольку только $\operatorname {int} (S\cup T)~\supseteq ~(\operatorname {int} S)\cup (\operatorname {int} T)$ в целом гарантируется, и равенство может не соблюдаться. Например, если $X=\mathbb {R} ,S=(-\infty ,0],$ и $T=(0,\infty )$ затем $(\operatorname {int} S)\cup (\operatorname {int} T)=(-\infty ,0)\cup (0,\infty )=\mathbb {R} \setminus \{0\}$ является правильным подмножеством $\operatorname {int} (S\cup T)=\operatorname {int} \mathbb {R} =\mathbb {R} .$
• Монотонный / неубывающий по $\subseteq$: Если $S\subseteq T$ затем $\operatorname {int} S\subseteq \operatorname {int} T.$

Другие свойства включают в себя:

• Если $S$ закрыт в $X$ и $\operatorname {int} T=\varnothing$ затем $\operatorname {int} (S\cup T)=\operatorname {int} S.$

Связь с закрытием

Приведенные выше утверждения останутся верными, если все экземпляры символов/слов

«внутренний», «int», «открытый», «подмножество» и «самый большой»

соответственно заменяются на

« закрытие », «cl», «закрытый», «суперсет» и «самый маленький».

и меняются местами следующие символы:

1. " $\subseteq$"поменялся местами" $\supseteq$"
2. " $\cup$"поменялся местами" $\cap$"

Более подробную информацию по этому вопросу см. в разделе «Внутренний оператор» ниже или в статье « Аксиомы замыкания Куратовского» .

Внутренний оператор

Внутренний оператор $\operatorname {int} _{X}$ двойственен оператору замыкания , который обозначается $\operatorname {cl} _{X}$ или через подчеркивание ^— , в том смысле, что $$\operatorname {int} _{X}S=X\setminus {\overline {(X\setminus S)}}$$а также $${\overline {S}}=X\setminus \operatorname {int} _{X}(X\setminus S),$$где $X$ — топологическое пространство, содержащее $S,$ и обратная косая черта $\,\setminus \,$ обозначает теоретико-множественную разницу .Следовательно, абстрактную теорию операторов замыкания и аксиомы замыкания Куратовского можно легко перевести на язык внутренних операторов, заменяя множества их дополнениями в $X.$

В общем, внутренний оператор не сотрудничает с профсоюзами. Однако в полном метрическом пространстве справедлив следующий результат:

Теорема  (Ч. Урсеску) — Пусть $S_{1},S_{2},\ldots$ быть последовательностью подмножеств полного метрического пространства $X.$

• Если каждый $S_{i}$ закрыт в $X$ затем $${\operatorname {cl} _{X}}{\biggl (}\bigcup _{i\in \mathbb {N} }\operatorname {int} _{X}S_{i}{\biggr )}={\operatorname {cl} _{X}\operatorname {int} _{X}}{\biggl (}\bigcup _{i\in \mathbb {N} }S_{i}{\biggr )}.$$
• Если каждый $S_{i}$ открыт в $X$ затем $${\operatorname {int} _{X}}{\biggl (}\bigcap _{i\in \mathbb {N} }\operatorname {cl} _{X}S_{i}{\biggr )}={\operatorname {int} _{X}\operatorname {cl} _{X}}{\biggl (}\bigcap _{i\in \mathbb {N} }S_{i}{\biggr )}.$$

Из приведенного выше результата следует, что каждое полное метрическое пространство является пространством Бэра .

Внешний вид набора

Внешний вид подмножества $S$ топологического пространства $X,$ обозначается $\operatorname {ext} _{X}S$ или просто $\operatorname {ext} S,$ является крупнейшим открытым множеством, не пересекающимся с $S,$ а именно, это объединение всех открытых множеств в $X$ которые не пересекаются с $S.$ Внешняя часть — это внутренняя часть дополнения, то же самое, что и дополнение замыкания; в формулах, $$\operatorname {ext} S=\operatorname {int} (X\setminus S)=X\setminus {\overline {S}}.$$

Точно так же внутреннее — это внешнее дополнение: $$\operatorname {int} S=\operatorname {ext} (X\setminus S).$$

Внутренняя часть, граница и внешняя часть множества. $S$ вместе разделите все пространство на три блока (или меньше, если один или несколько из них пусты): $$X=\operatorname {int} S\cup \partial S\cup \operatorname {ext} S,$$где $\partial S$ обозначает границу $S.$ Внутреннее и внешнее всегда открыто , а граница закрыта .

Некоторые свойства внешнего оператора отличаются от свойств внутреннего оператора:

• Внешний оператор меняет места включения; если $S\subseteq T,$ затем $\operatorname {ext} T\subseteq \operatorname {ext} S.$
• Внешний оператор не идемпотентен . Он обладает тем свойством, что $\operatorname {int} S\subseteq \operatorname {ext} \left(\operatorname {ext} S\right).$

Внутренне-непересекающиеся формы

Красные фигуры не пересекаются внутри с синим Треугольником. Зеленая и желтая формы внутренне не пересекаются с синим Треугольником, но только желтая форма полностью не пересекается с синим Треугольником.

Две формы $a$ и $b$ называются внутренне непересекающимися, если пересечение их внутренностей пусто.Внутренне-непересекающиеся фигуры могут пересекаться или не пересекаться на своих границах.

См. также

• Алгебраический интерьер - Обобщение топологического интерьера.
• ДЭ-9ИМ – Топологическая модель
• Внутренняя алгебра - Алгебраическая структура
• Теорема Жордана о кривой . Замкнутая кривая делит плоскость на две области.
• Квазиотносительный интерьер - Обобщение алгебраического интерьера.
• Относительный интерьер - Обобщение топологического интерьера.

Библиография

• Бурбаки, Николя (1989) [1966]. Общая топология: главы 1–4 [ Общая топология ]. Элементы математики . Берлин, Нью-Йорк: Springer Science & Business Media. ISBN  978-3-540-64241-1 . OCLC   18588129 .
• Диксмье, Жак (1984). Общая топология . Тексты для бакалавриата по математике. Перевод Berberian, SK New York: Springer-Verlag . ISBN  978-0-387-90972-1 . ОСЛК   10277303 .
• Часар, Акош (1978). Общая топология . Перевод Часара, Клары. Adam Hilger Ltd. Бристоль, Англия: ISBN  0-85274-275-4 . ОСЛК   4146011 .
• Дугунджи, Джеймс (1966). Топология . Бостон: Аллин и Бэкон. ISBN  978-0-697-06889-7 . OCLC   395340485 .
• Джоши, К.Д. (1983). Введение в общую топологию . Нью-Йорк: ISBN John Wiley and Sons Ltd.  978-0-85226-444-7 . OCLC   9218750 .
• Келли, Джон Л. (1975). Общая топология . Тексты для аспирантов по математике . Том. 27. Нью-Йорк: Springer Science & Business Media. ISBN  978-0-387-90125-1 . ОСЛК   338047 .
• Манкрес, Джеймс Р. (2000). Топология (Второе изд.). Река Аппер-Сэддл, Нью-Джерси : Prentice Hall, Inc. ISBN  978-0-13-181629-9 . OCLC   42683260 .
• Шуберт, Хорст (1968). Топология . Лондон: ISBN Macdonald & Co.  978-0-356-02077-8 . OCLC   463753 .
• Вилански, Альберт (17 октября 2008 г.) [1970]. Топология для анализа . Минеола, Нью-Йорк: ISBN Dover Publications, Inc.  978-0-486-46903-4 . OCLC   227923899 .
• Уиллард, Стивен (2004) [1970]. Общая топология . Минеола, Нью-Йорк : Dover Publications . ISBN  978-0-486-43479-7 . OCLC   115240 .

Внешние ссылки

• Интерьер в PlanetMath .