✖


Jump to content

Конформационная изомерия

(Перенаправлено из конформации Гоша )
Вращение вокруг одинарной связи бутана для взаимного преобразования одной конформации в другую. Конформация гош справа представляет собой конформер, а затменная конформация слева представляет собой переходное состояние между конформерами. Вверху: проекция Ньюмана; внизу: изображение пространственной ориентации.

В химии (см. рисунок , конформационная изомерия — это форма стереоизомерии , при которой изомеры могут взаимно превращаться просто путем вращения вокруг формально одинарных связей посвященный вращению одинарных связей). В то время как любые два расположения атомов в молекуле , которые различаются вращением вокруг одинарных связей, можно назвать разными конформациями , конформации, которые соответствуют локальным минимумам на поверхности потенциальной энергии, называются конформационными изомерами или конформерами . [1] Конформации, соответствующие локальным максимумам на энергетической поверхности, являются переходными состояниями между конформационными изомерами с локальным минимумом. Вращение вокруг одинарных связей предполагает преодоление вращательного энергетического барьера для взаимного преобразования одного конформера в другой. Если энергетический барьер низок, то существует свободное вращение. [2] и образец соединения существует как быстро уравновешивающая смесь множества конформеров; если энергетический барьер достаточно высок, то вращение ограничено, молекула может существовать в течение относительно длительного периода времени как стабильный вращательный изомер или ротамер (изомер, возникающий в результате затрудненного вращения одинарной связи). Когда временной интервал взаимного превращения достаточно велик для выделения отдельных ротамеров (обычно условно определяемый как период полураспада взаимного превращения 1000 секунд или более), изомеры называются атропоизомерами ( см.: атропоизомерия ). [1] [3] [4] замещенных Переворот кольца циклогексанов представляет собой еще одну распространенную форму конформационной изомерии.

Таким образом, конформационные изомеры отличаются от других классов стереоизомеров (т.е. конфигурационных изомеров), где взаимное превращение обязательно включает разрыв и реформирование химических связей. [5] Например, L / D- и R / S -конфигурации органических молекул имеют различную направленность и оптическую активность и могут быть взаимно преобразованы только путем разрыва одной или нескольких связей, связанных с хиральным атомом, и реформирования аналогичной связи в другом направлении или пространстве. ориентация. Они также отличаются от геометрических ( цис / транс ) изомеров, другого класса стереоизомеров, которым π-компонента двойных связей для взаимного превращения требуется разрыв . (Хотя различие не всегда четкое, поскольку некоторые связи, которые формально являются одинарными, на самом деле имеют характер двойной связи, который становится очевидным только тогда, когда рассматриваются вкладчики вторичного резонанса, например, связи C–N в амидах .) Из-за быстрое взаимное превращение, конформеры обычно не поддаются выделению при комнатной температуре.

Изучение энергетики между различными конформациями называется конформационным анализом . [6] Это полезно для понимания стабильности различных изомеров, например, путем учета пространственной ориентации и пространственных взаимодействий заместителей. Кроме того, конформационный анализ можно использовать для прогнозирования и объяснения селективности продуктов, механизмов и скорости реакций. [7] Конформационный анализ также играет важную роль в рациональном, основанном на структуре дизайне лекарств .

Типы

[ редактировать ]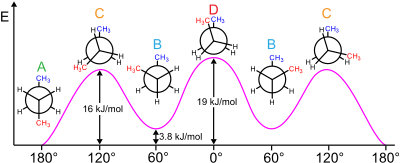
Относительная конформационная энергетическая диаграмма бутана в зависимости от двугранного угла. [8] А: антиперипланарный, анти или транс. Б: синклинальный или гош. C: антиклинальный или затменный. D: синперипланарный или цис. [1]

Вращая свои углерод-углеродные связи, молекулы этана и пропана имеют три локальных минимума энергии. Они структурно и энергетически эквивалентны и называются шахматными конформерами . Для каждой молекулы три заместителя, исходящие от каждой связи углерод-углерод, расположены в шахматном порядке, при этом каждый двугранный угол H-C-C-H (и двугранный угол H-C-C-CH 3 в случае пропана) равен 60°. (или примерно равен 60° в случае пропана). Три затменные конформации, в которых двугранные углы равны нулю, представляют собой переходные состояния (максимумы энергии), соединяющие два эквивалентных минимума энергии, шахматные конформеры.

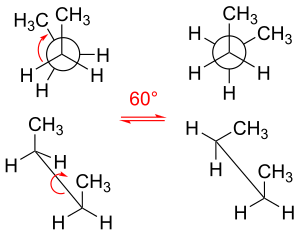
Молекула бутана — простейшая молекула, в которой вращение одинарных связей приводит к образованию двух типов неэквивалентных структур, известных как анти- и гош- конформеры (см. рисунок).

Например, бутан имеет три конформера, относящиеся к его двум метильным (CH 3 ) группам: два конформера гош , которые имеют расстояние между метилами ±60° и являются энантиомерными , и антиконформер , в котором четыре углеродных центра копланарны, а заместители расположены Расстояние друг от друга составляет 180 ° (см. Диаграмму свободной энергии бутана). Разница в энергии между гош и анти составляет 0,9 ккал/моль, что связано с энергией деформации конформера гош. Таким образом, антиконформер является наиболее стабильным (≈ 0 ккал/моль). Три затменные конформации с двугранными углами 0°, 120° и 240° являются переходными состояниями между конформерами. [6] Обратите внимание, что две затменные конформации имеют разную энергию: при 0 ° затмеваются две метильные группы, что приводит к более высокой энергии (≈ 5 ккал/моль), чем при 120 °, где метильные группы затмеваются водородами (≈ 3,5 ккал/моль). ). [9]

Хотя простые молекулы можно описать этими типами конформаций, более сложные молекулы требуют использования системы Клайна-Прелога для описания различных конформеров. [6]

Более конкретные примеры конформационной изомерии подробно описаны в другом месте:

Свободная энергия и равновесия конформационных изомеров

[ редактировать ]

Равновесие конформеров

[ редактировать ]
Равновесное распределение двух конформеров при разных температурах с учетом свободной энергии их взаимного превращения.

Конформационные изомеры существуют в динамическом равновесии , где относительная свободная энергия изомеров определяет заселенность каждого изомера, а энергетический барьер вращения определяет скорость взаимного превращения между изомерами: [11]

где K — константа равновесия, Δ G° — разность стандартной свободной энергии между двумя конформерами в ккал/моль, R — универсальная газовая постоянная (1,987×10 −3 ккал/моль К), а Т — температура системы в кельвинах . В единицах ккал/моль при 298 К,

Таким образом, каждые 1,36 ккал/моль соответствуют примерно 10-кратному коэффициенту константы равновесия при температурах, близких к комнатной. (Правило 1,36 в целом полезно для оценки констант равновесия при комнатной температуре по разнице свободной энергии. При более низких температурах для получения заданной константы равновесия необходима меньшая разность энергий.)

На схеме приведены три изотермы, изображающие равновесное распределение двух конформеров при разных температурах. При разнице свободной энергии 0 ккал/моль это дает константу равновесия 1, что означает, что два конформера существуют в соотношении 1:1. Оба имеют одинаковую свободную энергию; ни один из них не является более стабильным, поэтому ни один из них не преобладает по сравнению с другим. Отрицательная разница в свободной энергии означает, что конформер взаимно преобразуется в термодинамически более стабильную конформацию, поэтому константа равновесия всегда будет больше 1. Например, Δ G ° для превращения бутана из конформера гош в антиконформер равна -0,47 ккал/моль при 298 К. [12] Это дает константу равновесия примерно 2,2 в пользу антиконформера или смеси гош : антиконформеры в соотношении 31:69 в равновесии. И наоборот, положительная разница в свободной энергии означает, что конформер уже является более стабильным, поэтому взаимное превращение представляет собой неблагоприятное равновесие ( K < 1). Даже при крайне неблагоприятных изменениях (большие положительные ΔG ° ) константу равновесия между двумя конформерами можно увеличить за счет повышения температуры, так что количество менее стабильного конформера, присутствующего в равновесии, увеличивается (хотя он всегда остается второстепенным конформером).

Распределение популяции конформеров

[ редактировать ]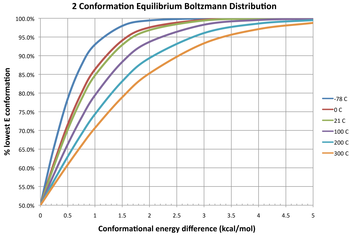
Распределение Больцмана, % конформации с наименьшей энергией в двухкомпонентной уравновешивающей системе при различных температурах (°C, цвет) и разнице энергий в ккал/моль ( x ) ось

Дробное распределение населения различных конформеров соответствует распределению Больцмана : [13]

Левая часть представляет собой долю конформера i в уравновешивающей смеси конформеров M , находящихся в термодинамическом равновесии. В правой части E k ( k = 1, 2, ..., M ) — энергия конформера k , R — молярная постоянная идеального газа (приблизительно равна 8,314 Дж/(моль·К) или 1,987 кал/ (моль·К)), а T — абсолютная температура . Знаменатель правой части — это статистическая сумма.

Факторы, способствующие свободной энергии конформеров

[ редактировать ]

Эффекты электростатических и стерических взаимодействий заместителей, а также орбитальных взаимодействий, таких как гиперконъюгация, ответственны за относительную стабильность конформеров и их переходных состояний. Вклад этих факторов варьируется в зависимости от природы заместителей и может способствовать как положительному, так и отрицательному вкладу в энергетический барьер. Вычислительные исследования малых молекул, таких как этан, показывают, что электростатические эффекты вносят наибольший вклад в энергетический барьер; однако барьер традиционно связывают в первую очередь со стерическими взаимодействиями. [14] [15]

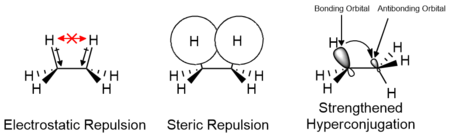
Вклад во вращательный энергетический барьер

В случае циклических систем стерический эффект и вклад в свободную энергию можно аппроксимировать значениями A , которые измеряют разницу энергий, когда заместитель в циклогексане находится в аксиальном положении по сравнению с экваториальным положением. В больших (>14 атомов) кольцах существует множество доступных низкоэнергетических конформаций, соответствующих недеформированной решетке алмаза. [16]

Выделение или наблюдение конформационных изомеров

[ редактировать ]

Короткие сроки взаимного превращения в большинстве случаев исключают разделение конформационных изомеров. Атропоизомеры представляют собой конформационные изомеры, которые можно разделить благодаря ограниченному вращению. [17] Равновесие между конформационными изомерами можно наблюдать с помощью различных спектроскопических методов .

Сворачивание белка также приводит к образованию стабильных конформационных изомеров, которые можно наблюдать. Уравнение Карплюса связывает двугранный угол вицинальных протонов с их константами J-связи , измеренными с помощью ЯМР. Уравнение помогает объяснить сворачивание белка, а также конформацию других жестких алифатических молекул. [18] Боковые цепи белков содержат ротамеры, распределение которых определяется их стерическим взаимодействием с различными конформациями основной цепи. [19] Это очевидно из статистического анализа конформаций боковых цепей белков в Backbone-зависимой библиотеке ротамеров .

В производных циклогексана два конформера кресла быстро взаимопревращаются при комнатной температуре, при этом сам циклогексан подвергается перевороту кольца со скоростью примерно 10 5 переворотов кольца в секунду, с общим энергетическим барьером 10 ккал/моль (42 кДж/моль), что исключает их разделение при температуре окружающей среды. [20] Однако при низких температурах ниже точки слияния можно напрямую контролировать равновесие с помощью ЯМР-спектроскопии и с помощью динамической, зависящей от температуры ЯМР-спектроскопии, барьерного взаимного превращения. [21]

Динамику конформационной (и других видов) изомерии можно отслеживать с помощью ЯМР- спектроскопии при различных температурах. Этот метод применим к барьерам 8–14 ккал/моль, и виды, демонстрирующие такую ​​динамику, часто называют « флюксными ».

Помимо ЯМР-спектроскопии, ИК-спектроскопия для измерения соотношения конформеров используется . Для аксиального и экваториального конформера бромциклогексана ν CBr различается почти на 50 см-1. −1 . [20]

Конформационно-зависимые реакции

[ редактировать ]

Скорость реакции сильно зависит от конформации реагентов. Во многих случаях доминирующий продукт возникает в результате реакции менее распространенного конформера в соответствии с принципом Кертина-Хаммета . Это типично для ситуаций, когда конформационное равновесие происходит гораздо быстрее, чем реакция образования продукта. Поэтому зависимость реакции от стереохимической ориентации обычно видна только у конфигурационных изомеров , у которых определенная конформация зафиксирована заместителями. Прогнозирование скоростей многих реакций, связанных с переходом между состояниями sp2 и sp3, таких как восстановление кетонов, окисление спиртов или нуклеофильное замещение, возможно, если все конформеры и их относительную стабильность, определяемую их штаммом . принять во внимание [22]

Одним из примеров конфигурационных изомеров являются реакции элиминирования , которые включают одновременное удаление протона и уходящей группы из вицинальных или антиперипланарных положений под влиянием основания.

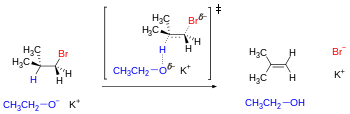
Бимолекулярное дегидрогалогенирование, индуцированное основаниями (механизм реакции типа Е2). Оптимальная геометрия переходного состояния требует, чтобы разрывающиеся связи были антиперипланарными, поскольку они находятся в соответствующей шахматной конформации.

Механизм требует, чтобы вылетающие атомы или группы следовали по антипараллельным траекториям. Для субстратов с открытой цепью этому геометрическому требованию отвечает по крайней мере один из трех расположенных в шахматном порядке конформеров. Однако для некоторых циклических субстратов, таких как циклогексан, антипараллельное расположение может быть недостижимо в зависимости от заместителей, которые могут устанавливать конформационный замок. [23] Соседние заместители в циклогексановом кольце могут достигать антиперипланарности только тогда, когда они занимают трансдиаксиальные положения (то есть оба находятся в аксиальном положении: один вверх, другой вниз).

Одним из последствий этого анализа является то, что транс- 4- трет -бутилциклогексилхлорид не может легко удалиться, а вместо этого подвергается замещению (см. диаграмму ниже), поскольку наиболее стабильная конформация имеет объемную группу t -Bu в экваториальном положении, поэтому хлоридная группа не антиперипланарно с любым вицинальным водородом (это бестактно для всех четырех). Термодинамически неблагоприятная конформация имеет в аксиальном положении группу t -Bu, которая выше по энергии более чем на 5 ккал/моль (см. значение А ). [24] В результате группа t -Bu «запирает» кольцо в той конформации, где оно находится в экваториальном положении и наблюдается реакция замещения. С другой стороны, цис -4- трет -бутилциклогексилхлорид подвергается элиминированию, поскольку антиперипланарность Cl и H может быть достигнута, когда группа t -Bu находится в благоприятном экваториальном положении.

Термодинамически неблагоприятная конформация транс -4- трет -бутилциклогексилхлорида, в которой группа t -Bu находится в аксиальном положении, осуществляя 7-атомные взаимодействия.
Транс - изомер может достичь антиперипланарности только через неблагоприятный аксиальный конформер; следовательно, это не устраняет. Цис - изомер уже имеет правильную геометрию в своей наиболее стабильной конформации; поэтому он легко устраняется.

Отталкивание между аксиальной т -бутильной группой и атомами водорода в 1,3-диаксиальном положении настолько сильное, что циклогексановое кольцо вернется к конформации скрученной лодочки . Деформация в циклических структурах обычно характеризуется отклонениями от идеальных валентных углов ( деформация Байера ), идеальных углов скручивания ( деформация Питцера ) или трансаннулярных (Прелог) взаимодействий.

Стереохимия алканов

[ редактировать ]
Конформации этана

Алкановые конформеры возникают в результате вращения вокруг sp 3 гибридизованные углерод-углеродные сигма-связи . Наименьший алкан с такой химической связью, этан , существует в виде бесконечного числа конформаций относительно вращения вокруг связи C–C. Два из них известны как формы минимума энергии ( шахматная конформация ) и максимума энергии ( затменная конформация ). Существование специфических конформаций обусловлено затрудненным вращением вокруг сигма-связей, хотя роль гиперконъюгации конкурирующая теория предполагает .

Важность минимумов и максимумов энергии проявляется в распространении этих концепций на более сложные молекулы, для которых можно предсказать стабильные конформации как формы с минимальной энергией. Определение стабильных конформаций также сыграло большую роль в создании концепции асимметричной индукции и возможности прогнозировать стереохимию реакций, контролируемых стерическими эффектами.

В примере шахматного этана в проекции Ньюмана атом водорода на одном атоме углерода имеет торсионный угол или торсионный угол 60 °. [25] относительно ближайшего атома водорода на другом углероде, так что стерические препятствия сводятся к минимуму. Ступенчатая конформация стабильнее на 12,5 кДж / моль , чем затменная конформация, которая является энергетическим максимумом для этана. В затменной конформации угол скручивания минимален.

шахматная конформация слева, затменная конформация справа в проекции Ньюмана
staggered conformation left, eclipsed conformation right in Newman projection

В бутане две смещенные конформации больше не эквивалентны и представляют собой два различных конформера: антиконформацию (крайняя левая, внизу) и конформацию гош (крайняя правая, внизу).

анти против бестактных конформаций
anti vs gauche conformations

Обе конформации свободны от деформации кручения, но в конформации гош две метильные группы находятся ближе, чем сумма их ван-дер-ваальсовых радиусов. Взаимодействие между двумя метильными группами является отталкивающим ( деформация Ван-дер-Ваальса ), в результате чего образуется энергетический барьер .

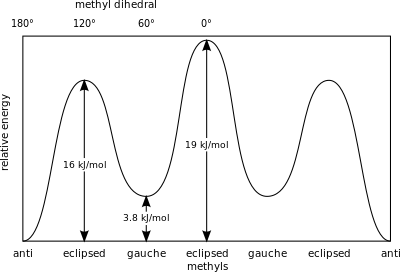
Мера потенциальной энергии, запасенной в бутановых конформерах с большими стерическими затруднениями, чем основное состояние «анти»-конформера, определяется следующими значениями: [26]

  • Слева, соответствует – 3,8 кДж/моль
  • Затмеваемые H и CH 3 – 16 кДж/моль
  • Затмеваемые СН 3 и СН 3 – 19 кДж/моль.

Затменные метильные группы оказывают большее стерическое напряжение из-за их большей электронной плотности по сравнению с одинокими атомами водорода .

Относительные энергии конформаций бутана относительно вращения центральной связи CC.

Хрестоматийное объяснение существования максимума энергии для затменной конформации в этане состоит в стерических затруднениях , но при длине связи CC 154 пм и радиусе Ван-дер-Ваальса для водорода 120 пм атомы водорода в этане никогда не находятся в путь друг друга. Вопрос о том, ответственны ли стерические препятствия за затменный максимум энергии, является предметом дискуссий и по сей день. Одна альтернатива объяснению стерических препятствий основана на гиперконъюгации , которая анализируется в рамках теории естественных орбитальных связей. [27] [28] [29] В шахматной конформации одна сигма- связывающая орбиталь CH передает электронную плотность разрыхляющей орбитали другой связи CH. Энергетическая стабилизация этого эффекта максимизируется, когда две орбитали имеют максимальное перекрытие, происходящее в шахматной конформации. В затменной конформации нет перекрытия, что приводит к невыгодному максимуму энергии. С другой стороны, анализ в рамках количественной теории молекулярных орбиталей показывает, что 2-орбитальные 4-электронные (стерические) отталкивания доминируют над гиперконъюгацией. [30] Исследование теории валентных связей также подчеркивает важность стерических эффектов. [31]

Номенклатура

[ редактировать ]

Именование алканов в соответствии со стандартами, перечисленными в Золотой книге ИЮПАК, осуществляется в соответствии с системой Клайна-Прелога для определения углов (называемых крутильными или двугранными углами ) между заместителями вокруг одинарной связи: [25]

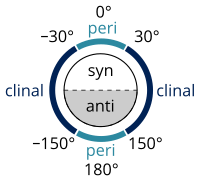
син/антипери/клинальный
syn/anti peri/clinal
  • угол скручивания от 0 ° до ± 90 ° называется Syn (s)
  • угол скручивания между ±90° и 180° называется анти (а)
  • угол скручивания между 30 ° и 150 ° или между -30 ° и -150 ° называется клиналом (c)
  • угол скручивания от 0 ° до ± 30 ° или от ± 150 ° до 180 ° называется перипланарным (p).
  • угол скручивания от 0° до ±30° называется синперипланарным (sp), также называемым син- или цис- конформацией.
  • угол скручивания от 30 ° до 90 ° и от -30 ° до -90 ° называется синклинальным (sc), также называемым гошем или перекосом. [32]
  • угол закручивания между 90 ° и 150 ° или от -90 ° до -150 ° называется антиклинальным (ac).
  • угол скручивания между ±150° и 180° называется антиперипланарным (ap), также называемым анти- или трансконформацией .

Деформация кручения или «деформация Питцера» относится к сопротивлению скручиванию связи.

Особые случаи

[ редактировать ]

В н -пентане концевые метильные группы испытывают дополнительное влияние пентана .

Замена водорода на фтор в политетрафторэтилене меняет стереохимию с зигзагообразной на геометрию спирали из-за электростатического отталкивания атомов фтора в положениях 1,3. Доказательства спиральной структуры в кристаллическом состоянии получены с помощью рентгеновской кристаллографии , ЯМР-спектроскопии и кругового дихроизма в растворе. [33]

См. также

[ редактировать ]
В Wikiquote есть цитаты, связанные с конформационной изомерией .

Ссылки

[ редактировать ]
  1. ^ Перейти обратно: а б с Мосс, врач общей практики (1 января 1996 г.). «Основная терминология стереохимии (Рекомендации ИЮПАК 1996 г.)» . Чистая и прикладная химия . 68 (12): 2193–2222. дои : 10.1351/pac199668122193 . ISSN   1365-3075 . S2CID   98272391 .
  2. ^ ИЮПАК , Сборник химической терминологии , 2-е изд. («Золотая книга») (1997). Онлайн исправленная версия: (1996) « Свободное вращение (затруднённое вращение, ограниченное вращение) ». дои : 10.1351/goldbook.F02520
  3. ^ Оки, Мичинори (1983) Последние достижения в области атропоизомерии, в разделе «Темы стереохимии» , Vol. 14 (Н.Л. Аллингер, Э.Л. Элиэль и С.Х. Вилен, ред.), Хобокен, Нью-Джерси: John Wiley & Sons, стр. 1–82; опубликовано в Интернете в 2007 г. , DOI: 10.1002/9780470147238.ch1, см. [1] и [2] [ постоянная мертвая ссылка ] , по состоянию на 12 июня 2014 г.
  4. ^ Алькорта, Ибон; Хосе Эльгеро; Кристиан Руссель; Николя Вантюин; Патрик Пирас (2012). Атропоизомерия и осевая хиральность в гетероароматических соединениях . Достижения гетероциклической химии. Том. 105. стр. 1–188. дои : 10.1016/B978-0-12-396530-1.00001-2 . hdl : 10261/62060 . ISBN  9780123965301 .
  5. ^ Хант, Ян. «Стереохимия» . Университет Калгари . Проверено 28 октября 2013 г.
  6. ^ Перейти обратно: а б с Анслин, Эрик; Деннис Догерти (2006). Современная физико-органическая химия . Университетская наука. п. 95 . ISBN  978-1891389313 .
  7. ^ Бартон, Дерек (1970). «Принципы конформационного анализа» . Нобель Медиа АБ 2013 . 169 (3945). Издательство Elsevier: 539–44. Бибкод : 1970Sci...169..539B . дои : 10.1126/science.169.3945.539 . ПМИД   17746022 . Проверено 10 ноября 2013 г.
  8. ^ Дж, Макмерри (2012). Органическая химия (8-е изд.). Бельмонт, Калифорния: Брукс/Коул. п. 98. ИСБН  9780840054449 .
  9. ^ Баулд, Натан. «Конформационный анализ бутана» . Техасский университет . Проверено 28 октября 2013 г.
  10. ^ Данбрэк, Р. (2002). «Библиотеки ротамеров в 21 веке». Современное мнение в области структурной биологии . 12 (4): 431–440. дои : 10.1016/S0959-440X(02)00344-5 . ПМИД   12163064 .
  11. ^ Бузик, Кароль. «Глава 6: Телосложение» . Университет Иллинойса в Чикаго . Архивировано из оригинала 11 ноября 2013 года . Проверено 10 ноября 2013 г.
  12. ^ Стандартное изменение энтальпии Δ H ° от гош до анти составляет –0,88 ккал/моль. Однако, поскольку существуют две возможные формы , существует статистический фактор, который необходимо учитывать как энтропийный член. Таким образом, ΔG ° = ΔH ° – T ΔS ° = ΔH ° + RT ln 2 = –0,88 ккал/моль + 0,41 ккал/моль = –0,47 ккал/моль, при 298 К.
  13. ^ Рзепа, Генри. «Конформационный анализ» . Имперский колледж Лондона . Проверено 11 ноября 2013 г.
  14. ^ Лю, Шубин (7 февраля 2013 г.). «Происхождение и природа барьеров вращения связей: единый взгляд». Журнал физической химии А. 117 (5): 962–965. Бибкод : 2013JPCA..117..962L . дои : 10.1021/jp312521z . ПМИД   23327680 .
  15. ^ Кэри, Фрэнсис А. (2011). Органическая химия (8-е изд.). Нью-Йорк: МакГроу-Хилл. п. 105 . ISBN  978-0-07-340261-1 .
  16. ^ Драгойлович, Велько (2015). «Конформационный анализ циклоалканов» (PDF) . Химтексты . 1 (3). дои : 10.1007/s40828-015-0014-0 . S2CID   94348487 .
  17. ^ Макнот (1997). «Атропизомеры» . Сборник химической терминологии ИЮПАК . Оксфорд: Научные публикации Блэквелла. дои : 10.1351/goldbook.A00511 . ISBN  978-0967855097 .
  18. ^ Далтон, Луиза. «Уравнение Карплюса» . Новости химии и техники . Американское химическое общество . Проверено 27 октября 2013 г.
  19. ^ Данбрек, РЛ; Коэн, FE (1997). «Байесовский статистический анализ предпочтений ротамеров боковой цепи белка» . Белковая наука . 6 (8): 1661–1681. дои : 10.1002/pro.5560060807 . ISSN   0961-8368 . ПМК   2143774 . ПМИД   9260279 .
  20. ^ Перейти обратно: а б Элиэль, Эль; Вилен, Ш.; Мандер, Л.Н. (1994). Стереохимия органических соединений . Дж. Уайли и сыновья. ISBN  978-0-471-01670-0 .
  21. ^ Дженсен, Фредерик Р.; Бушвеллер, К. Хакетт (1 июня 1969 г.). «Разделение конформеров. II. Осевые и экваториальные изомеры хлорциклогексана и тридейтериометоксициклогексана». Журнал Американского химического общества . 91 (12): 3223–3225. дои : 10.1021/ja01040a022 . ISSN   0002-7863 .
  22. ^ Шнайдер, Х.-Дж.; Шмидт, Г.; Томас Ф.Дж. Am. хим. Сок., 1983, 105, 3556. https://pubs.acs.org/doi/pdf/10.1021/ja00349a031
  23. ^ Рзепа, Генри С. (2014). «Циклоалканы» . Имперский колледж Лондона.
  24. ^ Догерти, Эрик В. Анслин; Деннис, А. (2006). Современная физико-органическая химия (ред. Додр.). Саусалито, Калифорния: Университетские научные книги. п. 104 . ISBN  978-1-891389-31-3 .
  25. ^ Перейти обратно: а б ИЮПАК , Сборник химической терминологии , 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) « Угол кручения ». два : 10.1351/goldbook.T06406
  26. ^ Макмерри, Дж. Э. (2003). Органическая химия (6-е изд.). Брукс Коул. ISBN  978-0534000134 .
  27. ^ Пофристик, Воислава; Гудман, Лайонел (2001). «Гиперконъюгация, а не стерическое отталкивание приводит к шахматной структуре этана» . Природа . 411 (6837): 565–568. дои : 10.1038/35079036 . ISSN   1476-4687 . ПМИД   11385566 .
  28. ^ Вейнхольд, Франк (2001). «Новый поворот в молекулярной форме». Природа . 411 (6837). ООО «Спрингер Сайенс энд Бизнес Медиа»: 539–541. дои : 10.1038/35079225 . ISSN   0028-0836 . ПМИД   11385553 .
  29. ^ Вайнхольд, Франк (15 сентября 2003 г.). «Опровержение аргумента Бикельхаупта-Бэрендса о стерическом отталкивании, вызывающем шахматную конформацию этана» . Angewandte Chemie, международное издание . 42 (35): 4188–4194. дои : 10.1002/anie.200351777 . ISSN   1433-7851 .
  30. ^ Бикельхаупт, Ф. Матиас; Баэрендс, Эверт Ян (15 сентября 2003 г.). «Дело о стерическом отталкивании, вызывающем шахматную конформацию этана». Angewandte Chemie (на немецком языке). 115 (35): 4315–4320. Бибкод : 2003АнгЧ.115.4315Б . дои : 10.1002/ange.200350947 . ISSN   0044-8249 .
  31. ^ Мо, Йиронг; Ву, Вэй; Сун, Линчунь; Линь, Мэнхай; Чжан, Цянер; Гао, Цзяли (30 марта 2004 г.). «Величина гиперконъюгации в этане: взгляд на теорию валентных связей Ab Initio». Angewandte Chemie, международное издание . 43 (15). Уайли: 1986–1990. дои : 10.1002/anie.200352931 . ISSN   1433-7851 . ПМИД   15065281 .
  32. ^ ИЮПАК , Сборник химической терминологии , 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) « Гош ». дои : 10.1351/goldbook.G02593
  33. ^ Конформационный анализ хиральных спиральных перфторалкильных цепей, проведенный VCD Кенджи Монде, Нобуаки Миура, Май Хашимото, Тору Танигучи и Тамоцу Инабе Дж. Ам. хим. Соц. ; 2006 год ; 128(18) стр. 6000–6001; Графическая абстракция
Retrieved from "https://en.wikipedia.org/w/index.php?title=Conformational_isomerism&oldid=1236437613"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: f292aedc1fff6393590ecf5ec121280c__1721833860
URL1:https://arc.ask3.ru/arc/aa/f2/0c/f292aedc1fff6393590ecf5ec121280c.html
Заголовок, (Title) документа по адресу, URL1:
Conformational isomerism - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)