Преобразование Гильберта

В математике и обработке сигналов представляет преобразование Гильберта собой особый сингулярный интеграл , который принимает функцию u ( t ) действительной переменной и создает другую функцию действительной переменной H( u )( t ) . Преобразование Гильберта задается главным значением Коши с свертки функцией $1/(\pi t)$ (см. § Определение ). Преобразование Гильберта имеет особенно простое представление в частотной области : оно придает фазовый сдвиг ±90° ( π /2 радиан) каждой частотной составляющей функции, причем знак сдвига зависит от знака частоты (см. § Связь с преобразованием Фурье ). Преобразование Гильберта важно при обработке сигналов, где оно является компонентом аналитического представления действительного сигнала u ( t ) . Преобразование Гильберта было впервые введено Дэвидом Гильбертом в этом контексте для решения частного случая проблемы Римана–Гильберта для аналитических функций.

Определение

Преобразование Гильберта u рассматривать как свертку u ) ( t можно с функцией h ( t ) = ⁠ 1 / π t ⁠ , известный как ядро ​​Коши . Поскольку 1/ t не интегрируется по t = 0 , интеграл, определяющий свертку, не всегда сходится. Вместо этого преобразование Гильберта определяется с использованием главного значения Коши (обозначенного здесь pv ). Явно преобразование Гильберта функции (или сигнала) u ( t ) определяется выражением

$$\operatorname {H} (u)(t)={\frac {1}{\pi }}\,\operatorname {p.v.} \int _{-\infty }^{+\infty }{\frac {u(\tau )}{t-\tau }}\,\mathrm {d} \tau ,$$

при условии, что этот интеграл существует как главное значение. Это и есть свертка u с умеренным распределением p.v. ⁠ 1 / π t ⁠ . В качестве альтернативы, заменяя переменные, интеграл главного значения можно записать явно как

$$\operatorname {H} (u)(t)={\frac {2}{\pi }}\,\lim _{\varepsilon \to 0}\int _{\varepsilon }^{\infty }{\frac {u(t-\tau )-u(t+\tau )}{2\tau }}\,\mathrm {d} \tau .$$

Когда преобразование Гильберта применяется дважды подряд к функции u , результат:

$$\operatorname {H} {\bigl (}\operatorname {H} (u){\bigr )}(t)=-u(t),$$

при условии, что интегралы, определяющие обе итерации, сходятся в подходящем смысле. В частности, обратное преобразование $-\operatorname {H}$. Этот факт легче всего увидеть, рассмотрев влияние преобразования Гильберта на Фурье u преобразование ( t ) (см. § Связь с преобразованием Фурье ниже).

Для аналитической функции в верхней полуплоскости преобразование Гильберта описывает связь между действительной и мнимой частью граничных значений. То есть, если f ( z ) аналитична в верхней полукомплексной плоскости { z : Im { z } > 0} и u ( t ) = Re { f ( t + 0· i )} , то Im { f ( t + 0· i )} = H( u )( t ) с точностью до аддитивной константы, при условии, что это преобразование Гильберта существует.

Обозначения

При обработке сигналов преобразование Гильберта u ( t ) обычно обозначается как ${\hat {u}}(t)$. Однако в математике это обозначение уже широко используется для обозначения преобразования Фурье u ( t ) . Иногда преобразование Гильберта может обозначаться как ${\tilde {u}}(t)$. Более того, многие источники определяют преобразование Гильберта как отрицательное по сравнению с определенным здесь.

История

Преобразование Гильберта возникло в работе Гильберта 1905 года по проблеме, поставленной Риманом относительно аналитических функций: которая стала известна как проблема Римана–Гильберта . Работа Гильберта в основном была связана с преобразованием Гильберта для функций, определенных на окружности. Некоторые из его ранних работ, связанных с дискретным преобразованием Гильберта, восходят к лекциям, которые он читал в Геттингене . Результаты были позже опубликованы Германом Вейлем в его диссертации. Шур улучшил результаты Гильберта о дискретном преобразовании Гильберта и распространил их на интегральный случай. Эти результаты были ограничены пространствами L ² и ℓ ² . В 1928 году Марсель Рис доказал, что преобразование Гильберта может быть определено для u в $L^{p}(\mathbb {R} )$ ( Л ^п пространстве ) для 1 < p < ∞ , что преобразование Гильберта является ограниченным оператором на $L^{p}(\mathbb {R} )$ для 1 < p < ∞ и что аналогичные результаты справедливы для преобразования Гильберта на окружности, а также для дискретного преобразования Гильберта. Преобразование Гильберта было мотивирующим примером для Антони Зигмунда и Альберто Кальдерона во время их изучения сингулярных интегралов . Их исследования сыграли фундаментальную роль в современном гармоническом анализе. Различные обобщения преобразования Гильберта, такие как билинейное и трилинейное преобразования Гильберта, до сих пор являются активными областями исследований.

Связь с преобразованием Фурье

Преобразование Гильберта является оператором умножения . Множитель H равен σ _H ( ω ) = − i sgn( ω ) , где Signum — сигнум-функция . Поэтому:

$${\mathcal {F}}{\bigl (}\operatorname {H} (u){\bigr )}(\omega )=-i\operatorname {sgn}(\omega )\cdot {\mathcal {F}}(u)(\omega ),$$

где ${\mathcal {F}}$ обозначает преобразование Фурье . Поскольку sn( x ) = sn(2 π x ) , отсюда следует, что этот результат применим к трем общим определениям ${\mathcal {F}}$.

По формуле Эйлера , $$\sigma _{\operatorname {H} }(\omega )={\begin{cases}~~i=e^{+i\pi /2},&{\text{for }}\omega <0,\\~~0,&{\text{for }}\omega =0,\\-i=e^{-i\pi /2},&{\text{for }}\omega >0.\end{cases}}$$

Следовательно, H( u )( t ) приводит к сдвигу фазы отрицательных частотных составляющих u ( t ) на +90° ( π ⁄ 2 радиан) и фаза положительных частотных составляющих на -90°, а i ·H( u )( t ) приводит к восстановлению положительных частотных составляющих при одновременном смещении отрицательных частотных составляющих еще на +90°, что приводит к в их отрицании (т.е. умножении на −1).

Когда преобразование Гильберта применяется дважды, фаза отрицательной и положительной частотных составляющих u ( t ) соответственно смещается на +180 ° и -180 °, что является эквивалентной величиной. Сигнал отрицается; т. е. H(H( u )) = − u , потому что

$$\left(\sigma _{\operatorname {H} }(\omega )\right)^{2}=e^{\pm i\pi }=-1\quad {\text{for }}\omega \neq 0.$$

Таблица избранных преобразований Гильберта

В следующей таблице частоты параметр $\omega$ реально.

Сигнал $u(t)$	Преобразование Гильберта $\operatorname {H} (u)(t)$
$\sin(\omega t+\varphi )$	${\begin{array}{lll}\sin \left(\omega t+\varphi -{\tfrac {\pi }{2}}\right)=-\cos \left(\omega t+\varphi \right),\quad \omega >0\\\sin \left(\omega t+\varphi +{\tfrac {\pi }{2}}\right)=\cos \left(\omega t+\varphi \right),\quad \omega <0\end{array}}$
$\cos(\omega t+\varphi )$	${\begin{array}{lll}\cos \left(\omega t+\varphi -{\tfrac {\pi }{2}}\right)=\sin \left(\omega t+\varphi \right),\quad \omega >0\\\cos \left(\omega t+\varphi +{\tfrac {\pi }{2}}\right)=-\sin \left(\omega t+\varphi \right),\quad \omega <0\end{array}}$
$e^{i\omega t}$	${\begin{array}{lll}e^{i\left(\omega t-{\tfrac {\pi }{2}}\right)},\quad \omega >0\\e^{i\left(\omega t+{\tfrac {\pi }{2}}\right)},\quad \omega <0\end{array}}$
$e^{-i\omega t}$	${\begin{array}{lll}e^{-i\left(\omega t-{\tfrac {\pi }{2}}\right)},\quad \omega >0\\e^{-i\left(\omega t+{\tfrac {\pi }{2}}\right)},\quad \omega <0\end{array}}$
$1 \over t^{2}+1$	$t \over t^{2}+1$
$e^{-t^{2}}$	${\frac {2}{\sqrt {\pi \,}}}F(t)$ (см. функцию Доусона )
Функция Sinc $\sin(t) \over t$	$1-\cos(t) \over t$
Дельта-функция Дирака $\delta (t)$	${1 \over \pi t}$
Характеристическая функция $\chi _{[a,b]}(t)$	${{\frac {1}{\,\pi \,}}\ln \left\vert {\frac {t-a}{t-b}}\right\vert }$

Примечания

Доступна обширная таблица преобразований Гильберта. Обратите внимание, что преобразование Гильберта константы равно нулю.

Область определения

Ни в коем случае не очевидно, что преобразование Гильберта вообще определено корректно, поскольку определяющий его несобственный интеграл должен сходиться в подходящем смысле. Однако преобразование Гильберта четко определено для широкого класса функций, а именно для функций из $L^{p}(\mathbb {R} )$ для 1 < п < ∞ .

Точнее, если ты в $L^{p}(\mathbb {R} )$ при 1 < p < ∞ предел, определяющий несобственный интеграл

$$\operatorname {H} (u)(t)={\frac {2}{\pi }}\lim _{\varepsilon \to 0}\int _{\varepsilon }^{\infty }{\frac {u(t-\tau )-u(t+\tau )}{2\tau }}\,d\tau$$

существует почти для каждого t . Функция предела также находится в $L^{p}(\mathbb {R} )$ и фактически является пределом среднего несобственного интеграла. То есть,

$${\frac {2}{\pi }}\int _{\varepsilon }^{\infty }{\frac {u(t-\tau )-u(t+\tau )}{2\tau }}\,\mathrm {d} \tau \to \operatorname {H} (u)(t)$$

при ε → 0 в L ^п норме, а также поточечно почти всюду по теореме Титчмарша .

В случае p = 1 преобразование Гильберта по-прежнему сходится поточечно почти всюду, но само по себе может оказаться неинтегрируемым даже локально. В частности, сходимости в среднем в этом случае вообще не происходит. Преобразование Гильберта L ¹ однако функция сходится в L ¹ -weak, а преобразование Гильберта — ограниченный оператор из L ¹ в Л ^{1, стих} . (В частности, поскольку преобразование Гильберта также является оператором-множителем на L ² , интерполяция Марцинкевича и аргумент двойственности дают альтернативное доказательство того, что H ограничено на L ^п .)

Характеристики

Ограниченность

Если 1 < p < ∞ , то преобразование Гильберта на $L^{p}(\mathbb {R} )$ — ограниченный линейный оператор , означающий, что существует константа C _p такая, что

$$\left\|\operatorname {H} u\right\|_{p}\leq C_{p}\left\|u\right\|_{p}$$

для всех $u\in L^{p}(\mathbb {R} )$.

Самая лучшая константа $C_{p}$ дается $$C_{p}={\begin{cases}\tan {\frac {\pi }{2p}}&{\text{for}}~1<p\leq 2,\\[4pt]\cot {\frac {\pi }{2p}}&{\text{for}}~2<p<\infty .\end{cases}}$$

Простой способ найти лучшее $C_{p}$ для $p$ быть степенью двойки - это благодаря так называемому тождеству Котлара, которое $(\operatorname {H} f)^{2}=f^{2}+2\operatorname {H} (f\operatorname {H} f)$ для всех действительных значений f . Те же лучшие константы справедливы и для периодического преобразования Гильберта.

Из ограниченности преобразования Гильберта следует $L^{p}(\mathbb {R} )$ сходимость симметричного оператора частичной суммы $$S_{R}f=\int _{-R}^{R}{\hat {f}}(\xi )e^{2\pi ix\xi }\,\mathrm {d} \xi$$

найти ​ в $L^{p}(\mathbb {R} )$.

Антисамосопряженность

Преобразование Гильберта является антисамосопряженным оператором относительно пары двойственности между $L^{p}(\mathbb {R} )$ и двойное пространство $L^{q}(\mathbb {R} )$, где p и q сопряжены по Гёльдеру и 1 < p , q < ∞ . Символически,

$$\langle \operatorname {H} u,v\rangle =\langle u,-\operatorname {H} v\rangle$$

для $u\in L^{p}(\mathbb {R} )$ и $v\in L^{q}(\mathbb {R} )$.

Обратное преобразование

Преобразование Гильберта — это антиинволюция . это означает, что

$$\operatorname {H} {\bigl (}\operatorname {H} \left(u\right){\bigr )}=-u$$

при условии, что каждое преобразование четко определено. Поскольку H сохраняет пространство $L^{p}(\mathbb {R} )$, это означает, в частности, что преобразование Гильберта обратимо на $L^{p}(\mathbb {R} )$, и это

$$\operatorname {H} ^{-1}=-\operatorname {H}$$

Сложная структура

Потому что Х ² = −I (« I » — тождественный оператор ) в реальном банаховом пространстве вещественных функций в $L^{p}(\mathbb {R} )$преобразование Гильберта определяет линейную комплексную структуру в этом банаховом пространстве. В частности, когда p = 2 , преобразование Гильберта дает гильбертово пространство вещественных функций в $L^{2}(\mathbb {R} )$ структура комплексного гильбертова пространства.

(Комплексные) собственные состояния преобразования Гильберта допускают представления в виде голоморфных функций в верхней и нижней полуплоскостях пространства Харди H ² по теореме Пэли-Винера .

Дифференциация

Формально производная преобразования Гильберта является преобразованием Гильберта производной, т.е. эти два линейных оператора коммутируют:

$$\operatorname {H} \left({\frac {\mathrm {d} u}{\mathrm {d} t}}\right)={\frac {\mathrm {d} }{\mathrm {d} t}}\operatorname {H} (u)$$

Повторяя это тождество,

$$\operatorname {H} \left({\frac {\mathrm {d} ^{k}u}{\mathrm {d} t^{k}}}\right)={\frac {\mathrm {d} ^{k}}{\mathrm {d} t^{k}}}\operatorname {H} (u)$$

Как уже говорилось, это строго верно при условии, что u и его первые k производные принадлежат $L^{p}(\mathbb {R} )$. Это легко проверить в частотной области, где дифференцирование превращается в умножение на ω .

Извилины

Преобразование Гильберта формально может быть реализовано как свертка с умеренным распределением

$$h(t)=\operatorname {p.v.} {\frac {1}{\pi \,t}}$$

Таким образом, формально

$$\operatorname {H} (u)=h*u$$

Однако априори это может быть определено только для носителя распределения компактного . С этим можно работать довольно строго, поскольку функции с компактным носителем (которые заведомо являются распределениями ) плотны в L ^п . В качестве альтернативы можно использовать тот факт, что h ( t ) является производной по распределению функции log| т |/ π ; а именно

$$\operatorname {H} (u)(t)={\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {1}{\pi }}\left(u*\log {\bigl |}\cdot {\bigr |}\right)(t)\right)$$

Для большинства операционных целей преобразование Гильберта можно рассматривать как свертку. Например, в формальном смысле преобразование Гильберта свертки — это свертка преобразования Гильберта, примененного только к одному из факторов:

$$\operatorname {H} (u*v)=\operatorname {H} (u)*v=u*\operatorname {H} (v)$$

Это строго верно, если u и v являются распределениями с компактным носителем, поскольку в этом случае

$$h*(u*v)=(h*u)*v=u*(h*v)$$

Таким образом, переходя к соответствующему пределу, верно и то, что u ∈ L ^п и v ∈ L ^д при условии, что

$$1<{\frac {1}{p}}+{\frac {1}{q}}$$

из теоремы Титчмарша.

Инвариантность

Преобразование Гильберта обладает следующими свойствами инвариантности на $L^{2}(\mathbb {R} )$.

• Он коммутирует с переводами. То есть он коммутирует с операторами T _a f ( x ) = f ( x + a ) для всех a в $\mathbb {R} .$
• Он коммутирует с положительными расширениями. То есть он коммутирует с операторами M _λ f ( x ) = f ( λ x ) для всех λ > 0 .
• Он антикоммутирует с отражением R f ( x ) знак равно f (− x ) .

С точностью до мультипликативной константы преобразование Гильберта является единственным ограниченным оператором в L ² с этими свойствами.

На самом деле существует более широкий набор операторов, коммутирующих с преобразованием Гильберта. Группа ${\text{SL}}(2,\mathbb {R} )$ действует унитарными операторами U _g в пространстве $L^{2}(\mathbb {R} )$ по формуле

$$\operatorname {U} _{g}^{-1}f(x)={\frac {1}{cx+d}}\,f\left({\frac {ax+b}{cx+d}}\right)\,,\qquad g={\begin{bmatrix}a&b\\c&d\end{bmatrix}}~,\qquad {\text{ for }}~ad-bc=\pm 1.$$

Это унитарное представление является примером представления основной серии . $~{\text{SL}}(2,\mathbb {R} )~.$ В этом случае оно приводимо и распадается как ортогональная сумма двух инвариантных подпространств, пространства Харди. $H^{2}(\mathbb {R} )$ и его сопряженное. Это пространства L ² граничные значения голоморфных функций на верхней и нижней полуплоскостях. $H^{2}(\mathbb {R} )$ и его сопряженное состоит именно из таких L ² функции с преобразованиями Фурье, обращающимися в нуль на отрицательной и положительной частях вещественной оси соответственно. Поскольку преобразование Гильберта равно H = − i (2 P − I) , где P является ортогональной проекцией из $L^{2}(\mathbb {R} )$ на $\operatorname {H} ^{2}(\mathbb {R} ),$ и I тождественный оператор , отсюда следует, что $\operatorname {H} ^{2}(\mathbb {R} )$ и его ортогональное дополнение являются собственными пространствами H для собственных значений ± i . Другими словами, H операторами Ug _{коммутирует с} . Ограничения операторов U _g на $\operatorname {H} ^{2}(\mathbb {R} )$ и его сопряженное число дают неприводимые представления ${\text{SL}}(2,\mathbb {R} )$ – так называемый предел представлений дискретной серии .

Расширение области определения

Преобразование Гильберта распределений

Кроме того, преобразование Гильберта можно распространить на определенные пространства распределений ( Pandey 1996 , глава 3). Поскольку преобразование Гильберта коммутирует с дифференцированием и является ограниченным оператором в L ^п , H ограничивается, чтобы дать непрерывное преобразование на обратном пределе пространств Соболева :

$${\mathcal {D}}_{L^{p}}={\underset {n\to \infty }{\underset {\longleftarrow }{\lim }}}W^{n,p}(\mathbb {R} )$$

Тогда преобразование Гильберта можно определить в двойственном пространстве ${\mathcal {D}}_{L^{p}}$, обозначенный ${\mathcal {D}}_{L^{p}}'$, состоящий из L ^п распределения. Это достигается за счет пары дуальности:
Для $u\in {\mathcal {D}}'_{L^{p}}$, определять:

$$\operatorname {H} (u)\in {\mathcal {D}}'_{L^{p}}=\langle \operatorname {H} u,v\rangle \ \triangleq \ \langle u,-\operatorname {H} v\rangle ,\ {\text{for all}}\ v\in {\mathcal {D}}_{L^{p}}.$$

Преобразование Гильберта можно определить и на пространстве умеренных распределений , используя подход Гельфанда и Шилова: но требуется значительно большая осторожность из-за сингулярности интеграла.

Преобразование Гильберта ограниченных функций

Преобразование Гильберта можно определить для функций из $L^{\infty }(\mathbb {R} )$ тоже, но требует некоторых модификаций и оговорок. При правильном понимании отображения преобразования Гильберта $L^{\infty }(\mathbb {R} )$ к банаховому пространству классов ограниченных средних колебаний (BMO).

При наивной интерпретации преобразование Гильберта ограниченной функции явно не определено. Например, при u = sn( x ) интеграл, определяющий H( u ), почти всюду расходится до ±∞ . Чтобы облегчить такие трудности, преобразование Гильберта L ^∞ Таким образом, функция определяется следующей регуляризованной формой интеграла

$$\operatorname {H} (u)(t)=\operatorname {p.v.} \int _{-\infty }^{\infty }u(\tau )\left\{h(t-\tau )-h_{0}(-\tau )\right\}\,\mathrm {d} \tau$$

где, как указано выше, h ( x ) = ⁠ 1 / πx ⁠ и

$$h_{0}(x)={\begin{cases}0&{\text{for}}~|x|<1\\{\frac {1}{\pi \,x}}&{\text{for}}~|x|\geq 1\end{cases}}$$

Модифицированное преобразование H согласуется с исходным преобразованием с точностью до аддитивной константы для функций компактного носителя из общего результата Кальдерона и Зигмунда. Более того, полученный интеграл почти всюду поточечно сходится по норме BMO к функции ограниченного среднего колебания.

Глубокий результат работы Феффермана заключается в том, что функция имеет ограниченное среднее колебание тогда и только тогда, когда она имеет форму f + H( g ) для некоторого $f,g\in L^{\infty }(\mathbb {R} )$.

Сопряженные функции

Преобразование Гильберта можно понимать в терминах пары функций f ( x ) и g ( x ) таких, что функция $$F(x)=f(x)+i\,g(x)$$ — граничное значение голоморфной функции F ( z ) в верхней полуплоскости. В этих обстоятельствах, если f и g достаточно интегрируемы, то одно является преобразованием Гильберта другого.

Предположим, что $f\in L^{p}(\mathbb {R} ).$ Тогда, согласно теории интеграла Пуассона , f допускает единственное гармоническое продолжение в верхнюю полуплоскость, и это расширение задается выражением

$$u(x+iy)=u(x,y)={\frac {1}{\pi }}\int _{-\infty }^{\infty }f(s)\;{\frac {y}{(x-s)^{2}+y^{2}}}\;\mathrm {d} s$$

что является сверткой f с ядром Пуассона

$$P(x,y)={\frac {y}{\pi \,\left(x^{2}+y^{2}\right)}}$$

Кроме того, существует единственная гармоническая функция v, определенная в верхней полуплоскости такая, что F ( z ) = u ( z ) + iv ( z ) голоморфна и $$\lim _{y\to \infty }v\,(x+i\,y)=0$$

Эта гармоническая функция получается из f путем свертки с сопряженным ядром Пуассона

$$Q(x,y)={\frac {x}{\pi \,\left(x^{2}+y^{2}\right)}}.$$

Таким образом $$v(x,y)={\frac {1}{\pi }}\int _{-\infty }^{\infty }f(s)\;{\frac {x-s}{\,(x-s)^{2}+y^{2}\,}}\;\mathrm {d} s.$$

Действительно, действительная и мнимая части ядра Коши равны $${\frac {i}{\pi \,z}}=P(x,y)+i\,Q(x,y)$$

так что F = u + iv голоморфно по интегральной формуле Коши .

Функция v, полученная из u таким образом, называется гармонически сопряженной к u . (Некасательный) граничный предел v ( x , y ) при y → 0 является преобразованием Гильберта f . Таким образом, вкратце, $$\operatorname {H} (f)=\lim _{y\to 0}Q(-,y)\star f$$

Теорема Титчмарша

Теорема Титчмарша (названная в честь Э. К. Титчмарша, который включил ее в свою работу 1937 года) уточняет связь между граничными значениями голоморфных функций в верхней полуплоскости и преобразованием Гильберта. Он дает необходимые и достаточные условия для того, чтобы комплекснозначная интегрируемая с квадратом функция F ( x ) на действительной прямой была граничным значением функции в пространстве Харди H. ² ( U ) голоморфных функций в верхней полуплоскости U .

Теорема утверждает, что следующие условия для комплекснозначной функции, интегрируемой с квадратом $F:\mathbb {R} \to \mathbb {C}$ эквивалентны:

• F ( x ) — предел при z → x голоморфной функции F ( z ) в верхней полуплоскости такой, что $$\int _{-\infty }^{\infty }|F(x+i\,y)|^{2}\;\mathrm {d} x<K$$
• Действительная и мнимая части F ( x ) являются преобразованиями Гильберта друг друга.
• Преобразование Фурье ${\mathcal {F}}(F)(x)$ исчезает при x < 0 .

Более слабый результат верен для функций класса L ^п для р > 1 . В частности, если F ( z ) — голоморфная функция такая, что

$$\int _{-\infty }^{\infty }|F(x+i\,y)|^{p}\;\mathrm {d} x<K$$

для всех y , то существует комплексная функция F ( x ) в $L^{p}(\mathbb {R} )$ такой, что F ( x + iy ) → F ( x ) в L ^п норма при y → 0 (а также поточечно почти всюду ). Более того,

$$F(x)=f(x)-i\,g(x)$$

где f — вещественная функция в $L^{p}(\mathbb {R} )$ g — преобразование Гильберта (класса L ^п ) выключенный .

Это неверно в случае p = 1 . Фактически, преобразование Гильберта L ¹ функция f не обязана сходиться в среднем к другому L ¹ функция. Тем не менее, преобразование Гильберта функции f сходится почти всюду к конечной функции g такой, что

$$\int _{-\infty }^{\infty }{\frac {|g(x)|^{p}}{1+x^{2}}}\;\mathrm {d} x<\infty$$

Этот результат прямо аналогичен результату Андрея Колмогорова для функций Харди в диске. Хотя этот результат обычно называют теоремой Титчмарша, он объединяет в себе большую часть работ других, в том числе Харди, Пейли и Винера (см. Теорему Пэли-Винера ), а также работы Рисса, Хилле и Тамаркина.

Проблема Римана–Гильберта

Одна из форм проблемы Римана–Гильберта направлена ​​на идентификацию пар функций F ₊ и F ₋ таких, что F ₊ голоморфен голоморфен в в верхней полуплоскости, а F ₋ нижней полуплоскости, так что для x вдоль действительной полуплоскости ось, $$F_{+}(x)-F_{-}(x)=f(x)$$

где f ( x ) — некоторая заданная вещественная функция от $x\in \mathbb {R}$. Левую часть этого уравнения можно понимать либо как разность пределов F _± от соответствующих полуплоскостей, либо как распределение гиперфункции . Две функции такого вида являются решением проблемы Римана–Гильберта.

Формально, если F _± решить задачу Римана–Гильберта $$f(x)=F_{+}(x)-F_{-}(x)$$

тогда преобразование Гильберта f ( x ) определяется выражением $$H(f)(x)=-i{\bigl (}F_{+}(x)+F_{-}(x){\bigr )}.$$

Преобразование Гильберта на окружности

См. Также: Пространство Харди

Для периодической функции f определено круговое преобразование Гильберта:

$${\tilde {f}}(x)\triangleq {\frac {1}{2\pi }}\operatorname {p.v.} \int _{0}^{2\pi }f(t)\,\cot \left({\frac {x-t}{2}}\right)\,\mathrm {d} t$$

Круговое преобразование Гильберта используется при описании пространства Харди и при изучении сопряженной функции в ряду Фурье. Ядро, $$\cot \left({\frac {x-t}{2}}\right)$$ известно как ядро ​​Гильберта , поскольку именно в этой форме первоначально изучалось преобразование Гильберта.

Ядро Гильберта (для кругового преобразования Гильберта) можно получить, сделав ядро ​​Коши 1 ⁄ х периодический. Точнее, при x ≠ 0

$${\frac {1}{\,2\,}}\cot \left({\frac {x}{2}}\right)={\frac {1}{x}}+\sum _{n=1}^{\infty }\left({\frac {1}{x+2n\pi }}+{\frac {1}{\,x-2n\pi \,}}\right)$$

Многие результаты о круговом преобразовании Гильберта могут быть получены из соответствующих результатов для преобразования Гильберта из этого соответствия.

Другая, более прямая связь, обеспечивается преобразованием Кэли C ( x ) = ( x – i ) / ( x + i ) , которое переносит действительную линию на круг, а верхнюю полуплоскость на единичный круг. Это индуцирует унитарное отображение

$$U\,f(x)={\frac {1}{(x+i)\,{\sqrt {\pi }}}}\,f\left(C\left(x\right)\right)$$

Л ​ ² ( Т ) на $L^{2}(\mathbb {R} ).$ Оператор U переносит пространство Харди H ² ( T ) на пространство Харди $H^{2}(\mathbb {R} )$.

Преобразование Гильберта в обработке сигналов

Теорема Бедросяна

Теорема Бедросяна утверждает, что преобразование Гильберта произведения низкочастотного и высокочастотного сигналов с неперекрывающимися спектрами определяется произведением низкочастотного сигнала и преобразования Гильберта высокочастотного сигнала, или

$$\operatorname {H} \left(f_{\text{LP}}(t)\cdot f_{\text{HP}}(t)\right)=f_{\text{LP}}(t)\cdot \operatorname {H} \left(f_{\text{HP}}(t)\right),$$

где f _LP и f _HP — сигналы нижних и верхних частот соответственно. Категория сигналов связи, к которым это применимо, называется моделью узкополосного сигнала. Членом этой категории является амплитудная модуляция высокочастотной синусоидальной «несущей»:

$$u(t)=u_{m}(t)\cdot \cos(\omega t+\varphi ),$$

где um _. ( t ) — сигнал «сообщения» с узкой полосой пропускания, например голос или музыка Тогда по теореме Бедросяна:

$$\operatorname {H} (u)(t)={\begin{cases}+u_{m}(t)\cdot \sin(\omega t+\varphi ),&\omega >0,\\-u_{m}(t)\cdot \sin(\omega t+\varphi ),&\omega <0.\end{cases}}$$

Аналитическое представление

Основная статья: аналитический сигнал

Конкретным типом сопряженной функции является :

$$u_{a}(t)\triangleq u(t)+i\cdot H(u)(t),$$

известное как представление аналитическое $u(t).$ Название отражает его математическую доступность, во многом благодаря формуле Эйлера . Применяя теорему Бедросяна к узкополосной модели, аналитическое представление имеет вид :

${\begin{aligned}u_{a}(t)&=u_{m}(t)\cdot \cos(\omega t+\varphi )+i\cdot u_{m}(t)\cdot \sin(\omega t+\varphi ),\quad \omega >0\\&=u_{m}(t)\cdot \left[\cos(\omega t+\varphi )+i\cdot \sin(\omega t+\varphi )\right],\quad \omega >0\\&=u_{m}(t)\cdot e^{i(\omega t+\varphi )},\quad \omega >0.\,\end{aligned}}$ ( Уравнение 1 )

Свойство преобразования Фурье указывает на то, что эта сложная операция может сдвинуть все отрицательные частотные компоненты um _{гетеродинная} ( t ) выше 0 Гц. В этом случае мнимая часть результата представляет собой преобразование Гильберта действительной части. Это косвенный способ получения преобразований Гильберта.

Угловая (фазовая/частотная) модуляция

Форма:

$$u(t)=A\cdot \cos(\omega t+\varphi _{m}(t))$$

называется угловой модуляцией , которая включает в себя как фазовую, так и частотную модуляцию . частота Мгновенная ​ $\omega +\varphi _{m}^{\prime }(t).$ При достаточно больших ω по сравнению с $\varphi _{m}^{\prime }$:

$$\operatorname {H} (u)(t)\approx A\cdot \sin(\omega t+\varphi _{m}(t))$$ и: $$u_{a}(t)\approx A\cdot e^{i(\omega t+\varphi _{m}(t))}.$$

Однополосная модуляция (SSB)

Основная статья: Однополосная модуляция

Когда um _также ( t ) в уравнении 1 является аналитическим представлением (формы сигнала сообщения), то есть:

$$u_{m}(t)=m(t)+i\cdot {\widehat {m}}(t)$$

в результате получается однополосная модуляция:

$$u_{a}(t)=(m(t)+i\cdot {\widehat {m}}(t))\cdot e^{i(\omega t+\varphi )}$$

передаваемый компонент которого:

$${\begin{aligned}u(t)&=\operatorname {Re} \{u_{a}(t)\}\\&=m(t)\cdot \cos(\omega t+\varphi )-{\widehat {m}}(t)\cdot \sin(\omega t+\varphi )\end{aligned}}$$

Причинность

Функция $h(t)=1/(\pi t)$ представляет две проблемы, основанные на причинно-следственной связи, для практической реализации в свертке (в дополнение к ее неопределенному значению, равному 0):

• Его длительность бесконечна (технически бесконечная поддержка ). конечной длины Окно уменьшает эффективный частотный диапазон преобразования; более короткие окна приводят к большим потерям на низких и высоких частотах. См. также квадратурный фильтр .
• Это непричинный фильтр . Итак, отложенная версия, $h(t-\tau ),$ требуется. Соответствующий вывод впоследствии задерживается на $\tau .$ При создании мнимой части аналитического сигнала источник (действительная часть) также должен быть задержан на $\tau$.

Дискретное преобразование Гильберта

Рисунок 1. Фильтр, частотная характеристика которого ограничена примерно 95 % частоты Найквиста.

Рисунок 2. Фильтр преобразования Гильберта с высокочастотной характеристикой.

Рисунок 3 .

Рисунок 4 . Преобразование Гильберта cos( ωt ) равно sin( ωt ) . На этом рисунке показаны sin(ωt) и два приближенных преобразования Гильберта, вычисленные библиотечной функцией MATLAB: Гильберт ()

Рисунок 5 . Дискретное преобразование Гильберта косинусоидальной функции с использованием кусочной свертки

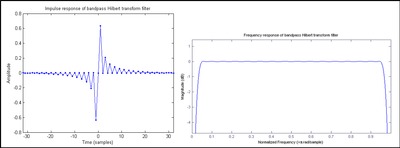
Для дискретной функции $u[n],$ с дискретным преобразованием Фурье (DTFT), $U(\omega )$и дискретное преобразование Гильберта ${\widehat {u}}[n],$ DTFT ${\widehat {u}}[n]$ в области − π < ω < π определяется выражением :

$\operatorname {DTFT} ({\widehat {u}})=U(\omega )\cdot (-i\cdot \operatorname {sgn}(\omega )).$

Обратное DTFT, используя теорему о свертке , имеет вид :

${\begin{aligned}{\widehat {u}}[n]&={\scriptstyle \mathrm {DTFT} ^{-1}}(U(\omega ))\ *\ {\scriptstyle \mathrm {DTFT} ^{-1}}(-i\cdot \operatorname {sgn}(\omega ))\\&=u[n]\ *\ {\frac {1}{2\pi }}\int _{-\pi }^{\pi }(-i\cdot \operatorname {sgn}(\omega ))\cdot e^{i\omega n}\,\mathrm {d} \omega \\&=u[n]\ *\ \underbrace {{\frac {1}{2\pi }}\left[\int _{-\pi }^{0}i\cdot e^{i\omega n}\,\mathrm {d} \omega -\int _{0}^{\pi }i\cdot e^{i\omega n}\,\mathrm {d} \omega \right]} _{h[n]},\end{aligned}}$

где

$h[n]\ \triangleq \ {\begin{cases}0,&{\text{for }}n{\text{ even}}\\{\frac {2}{\pi n}}&{\text{for }}n{\text{ odd}},\end{cases}}$

что представляет собой бесконечную импульсную характеристику (БИХ).

Практические соображения

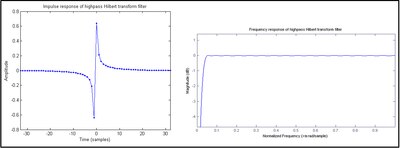
Метод 1: Прямая свертка потоковой передачи $u[n]$ данные с КИХ-аппроксимацией $h[n],$ который мы будем обозначать ${\tilde {h}}[n].$ Примеры усеченного $h[n]$ показаны на рисунках 1 и 2. Рис. 1 имеет нечетное число антисимметричных коэффициентов и называется типом III. Этот тип по своей сути демонстрирует отклики нулевой величины на частотах 0 и Найквиста, что приводит к форме полосового фильтра. Схема типа IV (четное число антисимметричных коэффициентов) показана на рис. 2 . Он имеет высокочастотную характеристику. Тип III – обычный выбор. по этим причинам :

• Типичный (т.е. правильно отфильтрованный и отобранный) $u[n]$ последовательность не имеет полезных компонентов на частоте Найквиста.
• Импульсная реакция типа IV требует ${\tfrac {1}{2}}$ сдвиг выборки в $h[n]$ последовательность. Это приводит к тому, что коэффициенты с нулевым значением становятся ненулевыми, как показано на рисунке 2 . Таким образом, конструкция типа III потенциально в два раза эффективнее типа IV.
• Групповая задержка конструкции типа III представляет собой целое число выборок, что облегчает выравнивание. ${\widehat {u}}[n]$ с $u[n]$ для создания аналитического сигнала . Групповая задержка типа IV находится на полпути между двумя выборками.

Резкое сокращение числа $h[n]$ создает рябь (эффект Гиббса) плоской частотной характеристики. Это можно смягчить, используя функцию окна для сужения. ${\tilde {h}}[n]$ до нуля.

Метод 2: Кусочная свертка. Хорошо известно, что прямая свертка требует гораздо больше вычислений, чем такие методы, как сохранение перекрытия , которые дают доступ к эффективности быстрого преобразования Фурье через теорему о свертке. В частности, дискретное преобразование Фурье (ДПФ) сегмента $u[n]$ умножается поточечно на ДПФ ${\tilde {h}}[n]$ последовательность. Для продукта выполняется обратное ДПФ, и переходные артефакты на переднем и заднем фронтах сегмента отбрасываются. Перекрывающиеся входные сегменты предотвращают разрывы в выходном потоке. Эквивалентное описание во временной области состоит в том, что сегменты длины $N$ (произвольный параметр) свернуты с периодической функцией :

${\tilde {h}}_{N}[n]\ \triangleq \sum _{m=-\infty }^{\infty }{\tilde {h}}[n-mN].$

При длительности ненулевых значений ${\tilde {h}}[n]$ является $M<N,$ выходная последовательность включает в себя $N-M+1$ образцы ${\widehat {u}}.$  $M-1$ выходные данные отбрасываются из каждого блока $N,$ и входные блоки перекрываются на эту величину, чтобы избежать пробелов.

Метод 3: То же, что и метод 2, за исключением ДПФ ${\tilde {h}}[n]$ заменяется образцами $-i\operatorname {sgn} (\omega )$ распределение (чьи действительные и мнимые компоненты всего лишь $0$ или $\pm 1.$) Это сворачивается $u[n]$ с периодическим суммированием :

$h_{N}[n]\ \triangleq \sum _{m=-\infty }^{\infty }h[n-mN],$   

для некоторого произвольного параметра, $N.$ $h[n]$ не является FIR, поэтому краевые эффекты распространяются на все преобразование. Решение о том, что удалять и какая степень перекрытия — это вопрос проектирования, зависящий от приложения.

На рис. 3 показана разница между методами 2 и 3. Показана только половина антисимметричной импульсной характеристики и только ненулевые коэффициенты. Синий график соответствует методу 2, где $h[n]$ усекается прямоугольной оконной функцией, а не сужается. Он генерируется функцией Matlab, hilb(65) . Его временные эффекты точно известны и легко отбрасываются. Частотная характеристика, которая определяется аргументом функции, является единственной проблемой проектирования, зависящей от приложения.

Красный график $h_{512}[n],$ соответствующий методу 3. Это обратное ДПФ $-i\operatorname {sgn} (\omega )$ распределение. В частности, это функция, свернутая с сегментом $u[n]$ функцией MATLAB , hilbert(u,512) , . Действительная часть выходной последовательности — это исходная входная последовательность, так что комплексный выход представляет собой представление аналитическое $u[n].$

Когда входными данными является сегмент чистого косинуса, результирующая свертка для двух разных значений $N$ изображено на рис. 4 (красный и синий графики). Краевые эффекты не позволяют результату быть чистой синусоидальной функцией (зеленый график). С $h_{N}[n]$ не является FIR-последовательностью, теоретический масштаб эффектов равен всей выходной последовательности. Но отличия от синусоидальной функции уменьшаются по мере удаления от краев. Параметр $N$ длина выходной последовательности. Если она превышает длину входной последовательности, входные данные изменяются путем добавления элементов с нулевым значением. В большинстве случаев это уменьшает величину краевых искажений. Но их продолжительность определяется присущими им периодами подъема и спада. $h[n]$ импульсный отклик.

На рис. 5 показан пример кусочной свертки с использованием обоих методов: 2 (синий) и 3 (красные точки). Синусоидальная функция создается путем вычисления дискретного преобразования Гильберта косинусоидальной функции, которая была обработана в четырех перекрывающихся сегментах и ​​снова собрана воедино. Как показывает результат БИХ (синий), искажения, видимые в результате БИХ (красный), не вызваны разницей между $h[n]$ и $h_{N}[n]$ (зеленый и красный на рис. 3 ). Тот факт, что $h_{N}[n]$ конус ( оконный ) действительно полезен в этом контексте. Настоящая проблема в том, что в нем недостаточно окон. Эффективно, $M=N,$ тогда как метод перекрытия-сохранения требует $M<N.$

Теоретико-числовое преобразование Гильберта

Теоретико-числовое преобразование Гильберта является расширением дискретного преобразования Гильберта к целым числам по модулю соответствующего простого числа. При этом следует обобщение дискретного преобразования Фурье на теоретико-числовые преобразования. Теоретико-числовое преобразование Гильберта можно использовать для генерации наборов ортогональных дискретных последовательностей.

См. также

• Аналитический сигнал
• Гармоническое сопряжение
• Гильбертова спектроскопия
• Преобразование Гильберта в комплексной плоскости
• Преобразование Гильберта – Хуанга
• Отношение Крамерса – Кронига
• Преобразование Рисса
• Однополосный сигнал
• Сингулярные интегральные операторы типа свертки

Ссылки

• Баргманн, В. (1947). «Неприводимые унитарные представления группы Лоренца». Энн. математики . 48 (3): 568–640. дои : 10.2307/1969129 . JSTOR   1969129 .
• Бедросян, Э. (декабрь 1962 г.). Теорема о произведении преобразований Гильберта (PDF) (Отчет). Корпорация Рэнд. РМ-3439-ПР.
• Бицадзе, А.В. (2001) [1994], "Краевые задачи аналитической теории функций" , Энциклопедия математики , EMS Press
• Брейсвелл, Р. (2000). Преобразование Фурье и его приложения (3-е изд.). МакГроу-Хилл. ISBN  0-07-116043-4 .
• Брандвуд, Дэвид (2003). Преобразования Фурье в радиолокации и обработке сигналов . Бостон: Артех Хаус. ISBN  9781580531740 .
• Кальдерон, AP ; Зигмунд, А. (1952). «О существовании некоторых сингулярных интегралов» . Акта Математика . 88 (1): 85–139. дои : 10.1007/BF02392130 .
• Каррик, Мэтт; Джагер, Дуг; Харрис, Фред (2011). Проектирование и применение трансформатора Гильберта в цифровом приемнике (PDF) . Шантильи, Вирджиния: Материалы технической конференции и выставки SDR 11, Форум беспроводных инноваций . Проверено 5 июня 2024 г.
• Дуоандикоэчеа, Дж. (2000). Фурье-анализ . Американское математическое общество. ISBN  0-8218-2172-5 .
• Дуистермаат, Джей-Джей ; Колк, JAC (2010). Распределения . Биркгаузер. дои : 10.1007/978-0-8176-4675-2 . ISBN  978-0-8176-4672-1 .
• Дюрен, П. (1970). Теория пространств H^p . Нью-Йорк, штат Нью-Йорк: Academic Press.
• Фефферман, К. (1971). «Характеристика ограниченного среднего колебания» . Бюллетень Американского математического общества . 77 (4): 587–588. дои : 10.1090/S0002-9904-1971-12763-5 . МР   0280994 .
• Фефферман, К.; Штейн, Э.М. (1972). «H^p пространства нескольких переменных» . Акта Математика . 129 : 137–193. дои : 10.1007/BF02392215 . МР   0447953 .
• Фрэнкс, Л.Е. (сентябрь 1969 г.). Томас Кайлат (ред.). Теория сигналов . Теория информации. Энглвуд Клиффс, Нью-Джерси: Прентис Холл. ISBN  0138100772 .
• Гельфанд, И.М. ; Шилов, Г.Е. (1968). Обобщенные функции . Том. 2. Академическая пресса. стр. 153–154. ISBN  0-12-279502-4 .
• Графакос, Лукас (2004). Классический и современный анализ Фурье . Пирсон Образование. стр. 253–257. ISBN  0-13-035399-Х .
• Харди, штат Джорджия ; Литтлвуд, JE ; Полиа, Г. (1952). Неравенства . Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  0-521-35880-9 .
• Гильберт, Дэвид (1953) [1912]. общей теории линейных интегральных уравнений ( Основы на немецком языке). Лейпциг и Берлин, Германия (1912 г.); Нью-Йорк, штат Нью-Йорк (1953): Б. Г. Тойбнер (1912); Паб Челси. Ко (1953). ISBN  978-3-322-00681-3 . OCLC   988251080 . Получено 18 декабря 2020 г. - через archive.org. {{cite book}}: CS1 maint: местоположение ( ссылка )
• Исукапалли, Йогананда. «Типы линейно-фазовых КИХ-фильтров» (PDF) . п. 18 . Проверено 8 июня 2024 г.
• Йоханссон, Матиас. «Преобразование Гильберта, магистерская диссертация» (PDF) . Архивировано из оригинала (PDF) 5 февраля 2012 г. ; также http://www.fuchs-braun.com/media/d9140c7b3d5004fbffff8007fffffff0.pdf. Архивировано 1 мая 2021 г. на Wayback Machine.
• Как, Субхаш (1970). «Дискретное преобразование Гильберта». Учеб. ИИЭЭ . 58 (4): 585–586. дои : 10.1109/PROC.1970.7696 .
• Как, Субхаш (2014). «Теоретико-числовое преобразование Гильберта». Схемы, системы и обработка сигналов . 33 (8): 2539–2548. arXiv : 1308.1688 . дои : 10.1007/s00034-014-9759-8 . S2CID   21226699 .
• Хведелидзе, Б.В. (2001) [1994], «Преобразование Гильберта» , Энциклопедия Математики , EMS Press
• Кинг, Фредерик В. (2009a). Преобразования Гильберта . Том. 1. Кембридж, Великобритания: Издательство Кембриджского университета.
• Кинг, Фредерик В. (2009b). Преобразования Гильберта . Том. 2. Кембридж, Великобритания: Издательство Кембриджского университета. п. 453. ИСБН  978-0-521-51720-1 .
• Кресс, Райнер (1989). Линейные интегральные уравнения . Нью-Йорк, штат Нью-Йорк: Springer-Verlag. стр. 91. ИСБН  3-540-50616-0 .
• Лонг, Серж (1985). СЛ(2, $\mathbb {R}$) . Тексты для аспирантов по математике. Том. 105. Нью-Йорк, штат Нью-Йорк: Springer-Verlag. ISBN  0-387-96198-4 .
• Осгуд, Брэд, Преобразование Фурье и его приложения (PDF) , Стэнфордский университет , получено 30 апреля 2021 г.
• Панди, Дж. Н. (1996). Преобразование Гильберта распределений Шварца и его приложения . Уайли-Интерсайенс. ISBN  0-471-03373-1 .
• Пихорид, С. (1972). «О наилучшем значении констант в теоремах Рисса, Зигмунда и Колмогорова» . Студия Математика . 44 (2): 165–179. дои : 10.4064/см-44-2-165-179 .
• Рабинер, Лоуренс Р.; Голд, Бернард (1975). Теория и применение цифровой обработки сигналов . Энглвуд Клиффс, Нью-Джерси: Прентис-Холл. ISBN  0-13-914101-4 .
• Рисс, Марсель (1928). «О сопряженных функциях». Математический журнал (на французском языке). 27 (1): 218–244. дои : 10.1007/BF01171098 . S2CID   123261514 .
• Розенблюм, Марвин; Ровняк, Джеймс (1997). Классы Харди и теория операторов . Дувр. ISBN  0-486-69536-0 .
• Шварц, Лоран (1950). Теория распределения . Париж, Франция: Германн.
• Шрайер, П.; Шарф, Л. (2010). Статистическая обработка сигналов комплексных данных: Теория несобственных и нециклических сигналов . Кембридж, Великобритания: Издательство Кембриджского университета.
• Смит, Дж. О. (2007). «Аналитические сигналы и фильтры преобразования Гильберта в математике дискретного преобразования Фурье (ДПФ) с аудиоприложениями» (2-е изд.) . Проверено 29 апреля 2021 г. ; также https://www.dsprelated.com/freebooks/mdft/Analytic_Signals_Hilbert_Transform.html

• Штейн, Элиас (1970). Сингулярные интегралы и свойства дифференцируемости функций . Издательство Принстонского университета. ISBN  0-691-08079-8 .
• Штейн, Элиас ; Вайс, Гвидо (1971). Введение в анализ Фурье в евклидовых пространствах . Издательство Принстонского университета. ISBN  0-691-08078-Х .
• Сугиура, Мицуо (1990). Унитарные представления и гармонический анализ: Введение . Математическая библиотека Северной Голландии. Том. 44 (2-е изд.). Эльзевир. ISBN  0444885935 .
• Титчмарш, Э. (1986) [1948]. Введение в теорию интегралов Фурье (2-е изд.). Оксфорд, Великобритания: Clarendon Press. ISBN  978-0-8284-0324-5 .
• Треттер, Стивен А. (1995). Р.В. Лаки (ред.). Проектирование систем связи с использованием алгоритмов DSP . Нью-Йорк: Спрингер. ISBN  0306450321 .
• Зигмунд, Антони (1988) [1968]. Тригонометрическая серия (2-е изд.). Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  978-0-521-35885-9 .

Дальнейшее чтение

• Бенедетто, Джон Дж. (1996). Гармонический анализ и его приложения . Бока-Ратон, Флорида: CRC Press. ISBN  0849378796 .
• Карлсон; Крилли и Ратледж (2002). Системы связи (4-е изд.). МакГроу-Хилл. ISBN  0-07-011127-8 .
• Голд, Б.; Оппенгейм, А.В.; Рейдер, CM (1969). «Теория и реализация дискретного преобразования Гильберта» (PDF) . Материалы симпозиума Бруклинского политехнического института 1969 года . Нью-Йорк . Проверено 13 апреля 2021 г.
• Графакос, Лукас (1994). «Элементарное доказательство квадратичной суммируемости дискретного преобразования Гильберта». Американский математический ежемесячник . 101 (5). Математическая ассоциация Америки: 456–458. дои : 10.2307/2974910 . JSTOR   2974910 .
• Титчмарш, Э. (1926). «Формулы взаимности с участием рядов и интегралов». Математический журнал . 25 (1): 321–347. дои : 10.1007/BF01283842 . S2CID   186237099 .

Внешние ссылки

• Вывод ограниченности преобразования Гильберта.
• Преобразование Гильберта Mathworld — Содержит таблицу преобразований.
• Вайсштейн, Эрик В. «Теорема Титчмарша» . Математический мир .
• «GS256 Лекция 3: Преобразование Гильберта» (PDF) . Архивировано из оригинала (PDF) 27 февраля 2012 г. введение начального уровня в преобразование Гильберта.