Комплексный многогранник
В геометрии комплексный многогранник — это обобщение многогранника в реальном пространстве до аналогичной структуры в комплексном гильбертовом пространстве , где каждое действительное измерение сопровождается мнимым .
Сложный многогранник можно понимать как совокупность комплексных точек, линий, плоскостей и т. д., где каждая точка является соединением нескольких прямых, каждая линия нескольких плоскостей и т. д.
Точные определения существуют только для правильных комплексных многогранников , которые являются конфигурациями . Правильные комплексные многогранники полностью охарактеризованы и могут быть описаны с использованием символической записи, разработанной Коксетером .
Также были описаны некоторые сложные многогранники, которые не являются полностью правильными.
Определения и введение
[ редактировать ]Сложная линия имеет одно измерение с реальными координатами, а другое с мнимыми координатами. Говорят, что применение реальных координат к обоим измерениям дает им два измерения по сравнению с действительными числами. Реальная плоскость с воображаемой осью, обозначенной как таковая, называется диаграммой Аргана . Из-за этого ее иногда называют комплексной плоскостью. Таким образом, комплексное двумерное пространство (также иногда называемое комплексной плоскостью) представляет собой четырехмерное пространство над реальными объектами и так далее в более высоких измерениях.
Комплексный n- многогранник в комплексном n -пространстве является аналогом вещественного n - многогранника в реальном n -пространстве. Однако не существует естественного комплексного аналога упорядочения точек на прямой (или связанных с ним комбинаторных свойств). Из-за этого сложный многогранник нельзя рассматривать как непрерывную поверхность и он не ограничивает внутреннюю часть, как это делает настоящий многогранник.
В случае правильных многогранников точное определение можно дать, используя понятие симметрии. Для любого правильного многогранника группа симметрии (здесь комплексная группа отражений , называемая группой Шепарда ) действует транзитивно на флаги , то есть на вложенные последовательности точек, содержащихся в прямой, содержащейся в плоскости, и так далее.
Более полно, скажем, что набор P аффинных подпространств (или квартир ) комплексного унитарного пространства V размерности n является правильным комплексным многогранником, если он удовлетворяет следующим условиям: [1] [2]
- для каждого −1 ⩽ i < j < k ⩽ n , если F — квартира в P размерности i, а H — квартира в P размерности k такая, что F ⊂ H , то существует по крайней мере две квартиры G в P размерности j такой, что F ⊂ G ⊂ H ;
- для каждого i , j такого, что −1 ⩽ i < j − 2, j ⩽ n , если F ⊂ G — квартиры P размеров i , j , то множество квартир между F и G связно в том смысле, что можно перейти от любого члена этого множества к любому другому с помощью последовательности вложений; и
- подмножество унитарных преобразований V , фиксирующих P транзитивно на флагах F 0 ⊂ F 1 ⊂ … ⊂ F n квартир P (причем Fi , размерности i для всех i ).
(Здесь под плоскостью размерности −1 понимается пустое множество.) Таким образом, по определению правильные комплексные многогранники представляют собой конфигурации в комплексном унитарном пространстве.
Правильные комплексные многогранники были открыты Шепардом (1952), а теория получила дальнейшее развитие Коксетером (1974).
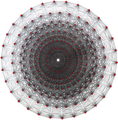
 Этот сложный многоугольник имеет 8 ребер (сложных линий), обозначенных как .. , h и 16 вершин. В каждом ребре лежат четыре вершины и в каждой вершине пересекаются два ребра. На левом изображении обведенные квадраты не являются элементами многогранника, а включены просто для того, чтобы помочь идентифицировать вершины, лежащие на одной сложной линии. Восьмиугольный периметр левого изображения не является элементом многогранника, а является многоугольником Петри . [3] На среднем изображении каждое ребро представлено в виде реальной линии, и четыре вершины в каждой линии видны более четко. |  Перспективный эскиз, представляющий 16 вершинных точек в виде больших черных точек и 8 4-ребер в виде ограниченных квадратов внутри каждого ребра. Зеленый путь представляет собой восьмиугольный периметр левого изображения. |
Комплексный многогранник существует в комплексном пространстве эквивалентной размерности. Например, вершины сложного многоугольника — это точки комплексной плоскости. (плоскость, в которой каждая точка имеет в качестве координат два комплексных числа, не путать с плоскостью Аргана комплексных чисел), а края представляют собой комплексные линии существующие как (аффинные) подпространства плоскости и пересекающиеся в вершинах. Таким образом, как одномерное комплексное пространство, ребру может быть присвоена собственная система координат, в которой каждая точка ребра представлена одним комплексным числом.
В правильном комплексном многограннике вершины, инцидентные ребру, расположены симметрично относительно их центроида , который часто используется в качестве начала системы координат ребра (в реальном случае центроид — это всего лишь середина ребра). Симметрия возникает из-за сложного отражения центроида; это отражение оставит величину любой вершины неизменной, но изменит ее аргумент на фиксированную величину, переместив его к координатам следующей по порядку вершины. Таким образом, мы можем предположить (после подходящего выбора масштаба), что вершины на ребре удовлетворяют уравнению где p — количество инцидентных вершин. Таким образом, в диаграмме Аргана ребра точки вершин лежат в вершинах правильного многоугольника с центром в начале координат.
Выше показаны три действительные проекции правильного комплексного многоугольника 4{4}2 с ребрами a, b, c, d, e, f, g, h . Он имеет 16 вершин, которые для ясности не отмечены индивидуально. Каждое ребро имеет четыре вершины, и каждая вершина лежит на двух ребрах, следовательно, каждое ребро пересекается с четырьмя другими ребрами. На первой диаграмме каждое ребро представлено квадратом. Стороны квадрата не являются частями многоугольника, а нарисованы исключительно для того, чтобы визуально связать четыре вершины. Края выкладываются симметрично. что диаграмма похожа на B 4 на плоскость Кокстера проекцию тессеракта (Обратите внимание , , но структурно отличается).
Средняя диаграмма отказывается от восьмиугольной симметрии в пользу ясности. Каждое ребро отображается как реальная линия, а каждая точка пересечения двух линий является вершиной. Связь между различными краями очевидна.
Последняя диаграмма дает представление о структуре, проецируемой в трех измерениях: два куба с вершинами на самом деле имеют одинаковый размер, но видны в перспективе на разных расстояниях в четвертом измерении.
Регулярные комплексные одномерные многогранники
[ редактировать ]
Настоящий одномерный многогранник существует как замкнутый отрезок вещественной прямой. , определяемый двумя конечными точками или вершинами линии. Его символ Шлефли — {} .
Аналогично, комплексный 1-многогранник существует как набор из p вершинных точек комплексной прямой. . Их можно представить как набор точек на диаграмме Аргана ( x , y )= x + iy . Правильный комплексный одномерный многогранник p {} имеет p ( p ≥ 2) точек вершин, расположенных так, чтобы образовывать выпуклый правильный многоугольник { p } на плоскости Аргана. [4]
В отличие от точек реальной линии, точки комплексной линии не имеют естественного порядка. Таким образом, в отличие от реальных многогранников, внутренняя часть не может быть определена. [5] Несмотря на это, сложные 1-многогранники часто изображают, как здесь, в виде ограниченного правильного многоугольника в плоскости Аргана.

Правильный действительный одномерный многогранник представляется пустым символом Шлефли {} или диаграммой Коксетера-Динкина. ![]() . Точка или узел диаграммы Кокстера-Динкина сама по себе представляет генератор отражения, а круг вокруг узла означает, что точка генератора не находится в отражении, поэтому ее отражающее изображение является отдельной точкой от самой себя. В более широком смысле, правильный комплексный одномерный многогранник в имеет диаграмму Кокстера-Динкина
. Точка или узел диаграммы Кокстера-Динкина сама по себе представляет генератор отражения, а круг вокруг узла означает, что точка генератора не находится в отражении, поэтому ее отражающее изображение является отдельной точкой от самой себя. В более широком смысле, правильный комплексный одномерный многогранник в имеет диаграмму Кокстера-Динкина ![]() , для любого положительного целого числа p , 2 или больше, содержащего p вершин. p может быть подавлен, если он равен 2. Он также может быть представлен пустым символом Шлефли p {}, } p {, {} p или p {2} 1 . 1 — это обозначение-заполнитель, представляющее несуществующее отражение или генератор идентификаторов периода 1. (0-многогранник, действительный или комплексный, является точкой и представлен как } { или 1 {2} 1 .)
, для любого положительного целого числа p , 2 или больше, содержащего p вершин. p может быть подавлен, если он равен 2. Он также может быть представлен пустым символом Шлефли p {}, } p {, {} p или p {2} 1 . 1 — это обозначение-заполнитель, представляющее несуществующее отражение или генератор идентификаторов периода 1. (0-многогранник, действительный или комплексный, является точкой и представлен как } { или 1 {2} 1 .)
Симметрия обозначается диаграммой Кокстера. ![]() , и альтернативно может быть описан в нотации Кокстера как p [], [] p или ] p [, p [2] 1 или p [1] p . Симметрия изоморфна циклической группе порядка p . [6] Подгруппами p [] являются любые целые дивизоры d , d [], где d ≥2.
, и альтернативно может быть описан в нотации Кокстера как p [], [] p или ] p [, p [2] 1 или p [1] p . Симметрия изоморфна циклической группе порядка p . [6] Подгруппами p [] являются любые целые дивизоры d , d [], где d ≥2.
Генератор унитарного оператора для ![]() рассматривается как поворот на 2π/ p радиан против часовой стрелки , а
рассматривается как поворот на 2π/ p радиан против часовой стрелки , а ![]() край создается последовательным применением одного унитарного отражения. Генератор унитарного отражения для 1-многогранника с p вершинами — это e 2π я / п = потому что (2π/ п ) + я грех (2π/ п ) . Когда p = 2, генератором является e π я = –1, то же самое, что и отражение точки в реальной плоскости.
край создается последовательным применением одного унитарного отражения. Генератор унитарного отражения для 1-многогранника с p вершинами — это e 2π я / п = потому что (2π/ п ) + я грех (2π/ п ) . Когда p = 2, генератором является e π я = –1, то же самое, что и отражение точки в реальной плоскости.
В более сложных многогранниках 1-многогранники образуют p -ребра. 2-ребро похоже на обычное вещественное ребро тем, что оно содержит две вершины, но не обязательно должно находиться на реальной линии.
Правильные сложные многоугольники
[ редактировать ]В то время как 1-многогранники могут иметь неограниченное количество p , конечные правильные комплексные многоугольники, за исключением многоугольников с двойной призмой p {4} 2 , ограничены элементами с 5 ребрами (пятиугольными ребрами), а бесконечные правильные апейрогоны также включают 6 ребер (шестиугольные ребра). элементы.
Обозначения
[ редактировать ]Модифицированная нотация Шепарда Шлефли
[ редактировать ]Первоначально Шепард разработал модифицированную форму обозначения Шлефли для правильных многогранников. Для многоугольника, ограниченного p 1 -ребрами, с p 2 -множеством в качестве вершины и общей группой симметрии порядка g , мы обозначаем многоугольник как p 1 ( g ) p 2 .
количество вершин V Тогда равно g / p 2 , а количество ребер E равно g / p 1 .
Сложный многоугольник, показанный выше, имеет восемь квадратных ребер ( p 1 =4) и шестнадцать вершин ( p 2 =2). Отсюда мы можем определить, что g = 32, что дает модифицированный символ Шлефли 4(32)2.
Пересмотренная модифицированная нотация Шлефли Коксетера
[ редактировать ]Более современное обозначение p 1 { q } p 2 принадлежит Кокстеру , [7] и основан на теории групп. Как группа симметрии, ее символ — p 1 [ q ] p 2 .
Группа симметрии p 1 [ q ] p 2 представлена 2 образующими R 1 , R 2 , где: R 1 п 1 = Р2 п 2 = I. Если q четное, (R 2 R 1 ) д /2 = (р 1 р 2 ) д /2 . Если q нечетно, (R 2 R 1 ) (q−1)/2 р 2 = (р 1 р 2 ) ( q −1)/2 Р 1 . Когда q нечетно p1 = p2 , .
Для 4 [4] 2 имеет R 1 4 = Р2 2 = Я, (Р 2 Р 1 ) 2 = (р 1 р 2 ) 2 .
Для 3 [5] 3 имеет R 1 3 = Р2 3 = Я, (Р 2 Р 1 ) 2 р 2 = (р 1 р 2 ) 2 Р1 .
Диаграммы Кокстера-Динкина
[ редактировать ]Коксетер также обобщил использование диаграмм Кокстера-Динкина на сложные многогранники, например, комплексный многоугольник p { q } r представлен формулой ![]()
![]()
![]() и эквивалентная группа симметрии p [ q ] r представляет собой диаграмму без колец.
и эквивалентная группа симметрии p [ q ] r представляет собой диаграмму без колец. ![]()
![]()
![]() . Узлы p и r представляют собой зеркала, создающие изображения p и r в плоскости. Непомеченные узлы на диаграмме имеют две неявные метки. Например, настоящий правильный многоугольник — это 2 { q } 2 или { q } или
. Узлы p и r представляют собой зеркала, создающие изображения p и r в плоскости. Непомеченные узлы на диаграмме имеют две неявные метки. Например, настоящий правильный многоугольник — это 2 { q } 2 или { q } или ![]()
![]()
![]() .
.
Одно ограничение: узлы, соединенные нечетными порядками ветвей, должны иметь одинаковые порядки узлов. Если этого не сделать, группа создаст «звездные» полигоны с перекрывающимися элементами. Так ![]()
![]()
![]() и
и ![]()
![]()
![]() являются обычными, в то время как
являются обычными, в то время как ![]()
![]()
![]() звездный.
звездный.
12 неприводимых групп Шепарда
[ редактировать ]
п [2 q ] 2 → п [ q ] п , индекс 2.
п [4] q → п [ q ] п , индекс q .

п [4] 2 → [ п ], индекс р
p [4] 2 → p [] × p [], индекс 2
Коксетер перечислил этот список правильных комплексных многоугольников в . Правильный комплексный многоугольник, p { q } r или ![]()
![]()
![]() , имеет p -ребра и r -угольные вершинные фигуры . p { q } r — конечный многогранник, если ( p + r ) q > pr ( q -2).
, имеет p -ребра и r -угольные вершинные фигуры . p { q } r — конечный многогранник, если ( p + r ) q > pr ( q -2).
Ее симметрия записывается как p [ q ] r , называемая группой Шепарда , аналогичной группе Кокстера , но также допускающей унитарные отражения .
Для незвездных групп порядок группы p [ q ] r можно вычислить как . [9]
Число Кокстера для p [ q ] r равно , поэтому порядок группы также можно вычислить как . Правильный комплексный многоугольник можно нарисовать в ортогональной проекции с h -угольной симметрией.
Решения ранга 2, которые генерируют сложные многоугольники:
| Группа | Г 3 =G( q ,1,1) | G2 р =G( , 1,2) | Г 4 | Г 6 | Г 5 | Г 8 | Г 14 | GG9 | Г 10 | GG20 | Г 16 | Г 21 | Г 17 | Г 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 [ q ] 2 , q =3,4... | р [4] 2 , р =2,3... | 3 [3] 3 | 3 [6] 2 | 3 [4] 3 | 4 [3] 4 | 3 [8] 2 | 4 [6] 2 | 4 [4] 3 | 3 [5] 3 | 5 [3] 5 | 3 [10] 2 | 5 [6] 2 | 5 [4] 3 | |
| Заказ | 2 кв. | 2 р 2 | 24 | 48 | 72 | 96 | 144 | 192 | 288 | 360 | 600 | 720 | 1200 | 1800 |
| час | д | 2 р | 6 | 12 | 24 | 30 | 60 | |||||||
Исключенные решения с нечетным q и неравными p и r : 6 [3] 2 , 6 [3] 3 , 9 [3] 3 , 12 [3] 3 , ..., 5 [5] 2 , 6 [5] 2 , 8 [5] 2 , 9 [5] 2 , 4 [7] 2 , 9 [5] 2 , 3 [9] 2 и 3 [11] 2 .
Другие целые q с неравными p и r создают звездные группы с перекрывающимися фундаментальными областями: ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() , и
, и ![]()
![]()
![]() .
.
Двойной многоугольник p { q } r — это r { q } p . Многоугольник вида p { q } p самодвойственный. Группы вида p [2 q ] 2 обладают полусимметрией p [ q ] p , поэтому правильный многоугольник ![]()
![]()
![]()
![]()
![]()
![]() то же самое, что и квазирегулярный
то же самое, что и квазирегулярный ![]()
![]()
![]()
![]()
![]() . А также правильный многоугольник с тем же порядком узлов,
. А также правильный многоугольник с тем же порядком узлов, ![]()
![]()
![]()
![]()
![]() , имеют альтернативную конструкцию
, имеют альтернативную конструкцию ![]()
![]()
![]()
![]()
![]()
![]() , что позволяет смежным краям иметь два разных цвета. [10]
, что позволяет смежным краям иметь два разных цвета. [10]
Порядок группы g используется для вычисления общего количества вершин и ребер. Он будет иметь вершины g / r и ребра g / p . Когда p = r , количество вершин и ребер одинаково. Это условие требуется, когда q нечетно.
Матричные генераторы
[ редактировать ]Группа p [ q ] r , ![]()
![]()
![]() , можно представить двумя матрицами: [11]
, можно представить двумя матрицами: [11]
| Имя | Р 1 | Р 2 |
|---|---|---|
| Заказ | п | р |
| Матрица |
С
- к=
- Примеры
|
|
| |||||||||||||||||||||||||||
|
|
|
Перечисление правильных комплексных многоугольников
[ редактировать ]Коксетер перечислил комплексные многоугольники в Таблице III Правильных комплексных многогранников. [12]
| Группа | Заказ | Коксетер число | Полигон | Вершины | Края | Примечания | ||
|---|---|---|---|---|---|---|---|---|
| G(д, д, 2) 2 [ q ] 2 = [ q ] д=2,3,4,... | 2 кв. | д | 2 { q } 2 | д | д | {} | Настоящие правильные многоугольники То же, что То же, что | |
| Группа | Заказ | Коксетер число | Полигон | Вершины | Края | Примечания | |||
|---|---|---|---|---|---|---|---|---|---|
| Г( п ,1,2) п [4] 2 р=2,3,4,... | 2 р 2 | 2 р | р (2 р 2 )2 | п {4} 2 | | п 2 | 2 р | п {} | то же, что p {} × p {} или представление в виде p - p- дуопризмы |
| 2( 2п 2 ) п | 2 {4} п | 2 р | п 2 | {} | представление в виде p - p- дуопирамиды | ||||
| Г(2,1,2) 2 [4] 2 = [4] | 8 | 4 | 2 {4} 2 = {4} | 4 | 4 | {} | то же, что {}×{} или Реальная площадь | ||
| Г(3,1,2) 3 [4] 2 | 18 | 6 | 6(18)2 | 3 {4} 2 | 9 | 6 | 3 {} | то же, что 3 {} × 3 {} или представительство в виде 3-3 дуопризмы | |
| 2(18)3 | 2 {4} 3 | 6 | 9 | {} | представление в виде 3-3 дуопирамид | ||||
| Г(4,1,2) 4 [4] 2 | 32 | 8 | 8(32)2 | 4 {4} 2 | 16 | 8 | 4 {} | то же, что 4 {} × 4 {} или представление в виде 4-4 дуопризм или {4,3,3} | |
| 2(32)4 | 2 {4} 4 | 8 | 16 | {} | представление в виде 4-4 дуопирамиды или {3,3,4} | ||||
| Г(5,1,2) 5 [4] 2 | 50 | 25 | 5(50)2 | 5 {4} 2 | 25 | 10 | 5 {} | то же, что 5 {}× 5 {} или представительство в виде 5-5-дуопризмы | |
| 2(50)5 | 2 {4} 5 | 10 | 25 | {} | представление в виде 5-5-дуопирамиды | ||||
| Г(6,1,2) 6 [4] 2 | 72 | 36 | 6(72)2 | 6 {4} 2 | 36 | 12 | 6 {} | то же, что 6 {} × 6 {} или представительство в виде 6-6 дуопризм | |
| 2(72)6 | 2 {4} 6 | 12 | 36 | {} | представление в виде 6-6 дуопирамид | ||||
| Г 4 =Г(1,1,2) 3 [3] 3 <2,3,3> | 24 | 6 | 3(24)3 | 3 {3} 3 | 8 | 8 | 3 {} | Конфигурация Мёбиуса – Кантора самодвойственный, то же, что представление как {3,3,4} | |
| Г 6 3 [6] 2 | 48 | 12 | 3(48)2 | 3 {6} 2 | 24 | 16 | 3 {} | то же, что | |
| 3 {3} 2 | звездный многоугольник | ||||||||
| 2(48)3 | 2 {6} 3 | 16 | 24 | {} | |||||
| 2 {3} 3 | звездный многоугольник | ||||||||
| Г 5 3 [4] 3 | 72 | 12 | 3(72)3 | 3 {4} 3 | 24 | 24 | 3 {} | самодвойственный, то же, что представление как {3,4,3} | |
| Г 8 4 [3] 4 | 96 | 12 | 4(96)4 | 4 {3} 4 | 24 | 24 | 4 {} | самодвойственный, то же, что представление как {3,4,3} | |
| Г 14 3 [8] 2 | 144 | 24 | 3(144)2 | 3 {8} 2 | 72 | 48 | 3 {} | то же, что | |
| 3 {8/3} 2 | звездный многоугольник, то же самое, что и | ||||||||
| 2(144)3 | 2 {8} 3 | 48 | 72 | {} | |||||
| 2 {8/3} 3 | звездный многоугольник | ||||||||
| GG9 4 [6] 2 | 192 | 24 | 4(192)2 | 4 {6} 2 | 96 | 48 | 4 {} | то же, что | |
| 2(192)4 | 2 {6} 4 | 48 | 96 | {} | |||||
| 4 {3} 2 | 96 | 48 | {} | звездный многоугольник | |||||
| 2 {3} 4 | 48 | 96 | {} | звездный многоугольник | |||||
| Г 10 4 [4] 3 | 288 | 24 | 4(288)3 | 4 {4} 3 | 96 | 72 | 4 {} | ||
| 12 | 4 {8/3} 3 | звездный многоугольник | |||||||
| 24 | 3(288)4 | 3 {4} 4 | 72 | 96 | 3 {} | ||||
| 12 | 3 {8/3} 4 | звездный многоугольник | |||||||
| GG20 3 [5] 3 | 360 | 30 | 3(360)3 | 3 {5} 3 | 120 | 120 | 3 {} | самодвойственный, то же, что представление как {3,3,5} | |
| 3 {5/2} 3 | самодвойственный звездный многоугольник | ||||||||
| Г 16 5 [3] 5 | 600 | 30 | 5(600)5 | 5 {3} 5 | 120 | 120 | 5 {} | самодвойственный, то же, что представление как {3,3,5} | |
| 10 | 5 {5/2} 5 | самодвойственный звездный многоугольник | |||||||
| Г 21 3 [10] 2 | 720 | 60 | 3(720)2 | 3 {10} 2 | 360 | 240 | 3 {} | то же, что | |
| 3 {5} 2 | звездный многоугольник | ||||||||
| 3 {10/3} 2 | звездный многоугольник, то же самое, что и | ||||||||
| 3 {5/2} 2 | звездный многоугольник | ||||||||
| 2(720)3 | 2 {10} 3 | 240 | 360 | {} | |||||
| 2 {5} 3 | звездный многоугольник | ||||||||
| 2 {10/3} 3 | звездный многоугольник | ||||||||
| 2 {5/2} 3 | звездный многоугольник | ||||||||
| Г 17 5 [6] 2 | 1200 | 60 | 5(1200)2 | 5 {6} 2 | 600 | 240 | 5 {} | то же, что | |
| 20 | 5 {5} 2 | звездный многоугольник | |||||||
| 20 | 5 {10/3} 2 | звездный многоугольник | |||||||
| 60 | 5 {3} 2 | звездный многоугольник | |||||||
| 60 | 2(1200)5 | 2 {6} 5 | 240 | 600 | {} | ||||
| 20 | 2 {5} 5 | звездный многоугольник | |||||||
| 20 | 2 {10/3} 5 | звездный многоугольник | |||||||
| 60 | 2 {3} 5 | звездный многоугольник | |||||||
| Г 18 5 [4] 3 | 1800 | 60 | 5(1800)3 | 5 {4} 3 | 600 | 360 | 5 {} | ||
| 15 | 5 {10/3} 3 | звездный многоугольник | |||||||
| 30 | 5 {3} 3 | звездный многоугольник | |||||||
| 30 | 5 {5/2} 3 | звездный многоугольник | |||||||
| 60 | 3(1800)5 | 3 {4} 5 | 360 | 600 | 3 {} | ||||
| 15 | 3 {10/3} 5 | звездный многоугольник | |||||||
| 30 | 3 {3} 5 | звездный многоугольник | |||||||
| 30 | 3 {5/2} 5 | звездный многоугольник | |||||||
Визуализации правильных сложных многоугольников
[ редактировать ]Многоугольники формы p {2 r } q можно визуализировать с помощью q наборов цветов p -ребра. Каждое p -ребро рассматривается как правильный многоугольник, при этом грани отсутствуют.
- 2D ортогональные проекции комплексных многоугольников 2 { r } q
Многоугольники вида 2 {4} q называются обобщенными ортоплексами . Они имеют общие вершины с 4D q - - q дуопирамидами , вершины которых соединены 2-ребрами.
- 2 {4} 2 ,


 , с 4 вершинами и 4 ребрами
, с 4 вершинами и 4 ребрами - 2 {4} 3 ,


 , с 6 вершинами и 9 ребрами [13]
, с 6 вершинами и 9 ребрами [13] - 2 {4} 4 ,


 , с 8 вершинами и 16 ребрами
, с 8 вершинами и 16 ребрами - 2 {4} 5 ,


 , с 10 вершинами и 25 ребрами
, с 10 вершинами и 25 ребрами - 2 {4} 6 ,


 , с 12 вершинами и 36 ребрами
, с 12 вершинами и 36 ребрами - 2 {4} 7 ,


 , с 14 вершинами и 49 ребрами
, с 14 вершинами и 49 ребрами - 2 {4} 8 ,


 , с 16 вершинами и 64 ребрами
, с 16 вершинами и 64 ребрами - 2 {4} 9 ,


 , с 18 вершинами и 81 ребром
, с 18 вершинами и 81 ребром - 2 {4} 10 ,


 , с 20 вершинами и 100 ребрами
, с 20 вершинами и 100 ребрами
- Комплексные многоугольники p {4} 2
Многоугольники вида p {4} 2 называются обобщенными гиперкубами (квадратами для многоугольников). Они имеют общие вершины с 4D p - p дуопризмами , вершины которых соединены p-ребрами. Вершины рисуются зеленым цветом, а p -ребра — чередующимися цветами: красным и синим. Перспектива немного искажается для нечетных размеров, чтобы переместить перекрывающиеся вершины из центра.
- 2 {4} 2 ,


 или
или 

 , с 4 вершинами и 4 2-ребрами
, с 4 вершинами и 4 2-ребрами - 4 {4} 2 ,


 или
или 

 , с 16 вершинами и 8 (квадратными) 4-ребрами
, с 16 вершинами и 8 (квадратными) 4-ребрами - 5 {4} 2 ,


 или
или 

 , с 25 вершинами и 10 (пятиугольными) 5-ребрами
, с 25 вершинами и 10 (пятиугольными) 5-ребрами - 6 {4} 2 ,


 или
или 

 , с 36 вершинами и 12 (шестиугольными) 6-ребрами
, с 36 вершинами и 12 (шестиугольными) 6-ребрами - 7 {4} 2 ,


 или
или 

 , с 49 вершинами и 14 (семиугольными)7-ребрами
, с 49 вершинами и 14 (семиугольными)7-ребрами - 8 {4} 2 ,


 или
или 

 , с 64 вершинами и 16 (восьмиугольными) 8-ребрами
, с 64 вершинами и 16 (восьмиугольными) 8-ребрами - 9 {4} 2 ,


 или
или 

 , с 81 вершиной и 18 (эннеагональными) 9-ребрами
, с 81 вершиной и 18 (эннеагональными) 9-ребрами - 10 {4} 2 ,


 или
или 

 , со 100 вершинами и 20 (десятиугольными) 10-ребрами
, со 100 вершинами и 20 (десятиугольными) 10-ребрами
- 3D перспективные проекции сложных многоугольников p {4} 2 . Двойники 2 {4} p
- видны путем добавления вершин внутри ребер и добавления ребер вместо вершин.
- 3 {4} 2 ,


 или
или 

 с 9 вершинами, 6 3-ребрами в 2 наборах цветов
с 9 вершинами, 6 3-ребрами в 2 наборах цветов - 2 {4} 3 ,


 с 6 вершинами, 9 ребрами в 3 наборах
с 6 вершинами, 9 ребрами в 3 наборах - 4 {4} 2 ,


 или
или 

 с 16 вершинами, 8 4-ребрами в 2 наборах цветов и заполненными квадратными 4-ребрами
с 16 вершинами, 8 4-ребрами в 2 наборах цветов и заполненными квадратными 4-ребрами - 5 {4} 2 ,


 или
или 

 с 25 вершинами, 10 5-ребрами в 2 наборах цветов
с 25 вершинами, 10 5-ребрами в 2 наборах цветов
- Другие сложные многоугольники p { r } 2
- 3 {6} 2 ,


 или
или 

 , с 24 вершинами черного цвета и 16 3-ребрами, окрашенными в 2 набора 3-ребер красного и синего цветов. [14]
, с 24 вершинами черного цвета и 16 3-ребрами, окрашенными в 2 набора 3-ребер красного и синего цветов. [14] - 3 {8} 2 ,


 или
или 

 , с 72 вершинами черного цвета и 48 3-ребрами, окрашенными в 2 набора 3-ребер красного и синего цветов. [15]
, с 72 вершинами черного цвета и 48 3-ребрами, окрашенными в 2 набора 3-ребер красного и синего цветов. [15]
- 2D ортогональные проекции комплексных многоугольников, p { r } p
Многоугольники вида p { r } p имеют одинаковое количество вершин и ребер. Они также самодвойственны.
- 3 {4} 3 ,


 или
или 

 , с 24 вершинами и 24 3-ребрами, показанными в 3 наборах цветов, один набор заполнен [17]
, с 24 вершинами и 24 3-ребрами, показанными в 3 наборах цветов, один набор заполнен [17]
Регулярные комплексные многогранники
[ редактировать ]В общем, правильный комплексный многогранник представляется Кокстером как p { z 1 } q {z 2 } r {z 3 } s … или диаграмма Кокстера ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …, обладающие симметрией p [ z 1 ] q [ z 2 ] r [ z 3 ] s … или
…, обладающие симметрией p [ z 1 ] q [ z 2 ] r [ z 3 ] s … или ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …. [20]
…. [20]
Существуют бесконечные семейства правильных комплексных многогранников, которые встречаются во всех измерениях, обобщая гиперкубы и перекрестные многогранники в реальном пространстве. «Обобщенный ортотоп» Шепарда обобщает гиперкуб; у него есть символ, заданный γ п
n = p {4} 2 {3} 2 … 2 {3} 2 и диаграмма ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …
… ![]()
![]()
![]()
![]()
![]() . Его группа симметрии имеет диаграмму p [4] 2 [3] 2 … 2 [3] 2 ; в классификации Шепарда-Тодда это группа G( p , 1, n ), обобщающая знаковые матрицы перестановок. Его двойственный правильный многогранник, «обобщенный перекрестный многогранник», обозначается символом β. п
. Его группа симметрии имеет диаграмму p [4] 2 [3] 2 … 2 [3] 2 ; в классификации Шепарда-Тодда это группа G( p , 1, n ), обобщающая знаковые матрицы перестановок. Его двойственный правильный многогранник, «обобщенный перекрестный многогранник», обозначается символом β. п
п = 2 {3} 2 {3} 2 … 2 {4} п и диаграмма ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …
… ![]()
![]()
![]()
![]() . [21]
. [21]
Одномерный правильный комплексный многогранник в представлен как ![]() , имеющий p вершин, с его действительным представлением в виде правильного многоугольника { p }. Коксетер также дает ему символ γ. п
, имеющий p вершин, с его действительным представлением в виде правильного многоугольника { p }. Коксетер также дает ему символ γ. п
1 или β п
1 как одномерный обобщенный гиперкуб или перекрестный многогранник. Его симметрия равна p [] или ![]() , циклическая группа порядка p . В более высоком многограннике p {} или
, циклическая группа порядка p . В более высоком многограннике p {} или ![]() представляет элемент p -ребра с 2-краем, {} или
представляет элемент p -ребра с 2-краем, {} или ![]() , представляющий обычное вещественное ребро между двумя вершинами. [21]
, представляющий обычное вещественное ребро между двумя вершинами. [21]
Двойственный комплексный многогранник строится путем замены k и ( n -1- k )-элементов n -многогранника. Например, двойственный комплексный многоугольник имеет вершины, центрированные по каждому краю, а новые ребра центрируются по старым вершинам. Вершина v -валентности создает новое v -ребро, а e -ребра становятся e -валентности. вершинами [22] Двойственный правильному комплексному многограннику имеет перевернутый символ. Правильные комплексные многогранники с симметричными символами, т.е. p { q } p , p { q } r { q } p , p { q } r { s } r { q } p и т. д. являются самодвойственными .
Перечисление правильных комплексных многогранников
[ редактировать ]
Коксетер перечислил этот список незвездных правильных комплексных многогранников в , включая 5 платоновых тел в . [23]
Правильный комплексный многогранник, p { n 1 } q { n 2 } r или ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеет
, имеет ![]()
![]()
![]()
![]()
![]()
![]() лица,
лица, ![]() края, и
края, и ![]()
![]()
![]()
![]()
![]()
![]() вершинные фигуры .
вершинные фигуры .
Комплексный правильный многогранник p { n 1 } q { n 2 } r требует, чтобы g 1 = order( p [ n 1 ] q ) и g 2 = order( q [ n 2 ] r ) были конечными.
Учитывая g = order( p [ n 1 ] q [ n 2 ] r ), количество вершин равно g / g 2 , а количество граней равно g / g 1 . Число ребер равно g / pr .
| Космос | Группа | Заказ | Номер Кокстера | Полигон | Вершины | Края | Лица | Вертекс фигура | Ван Ус многоугольник | Примечания | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Г(1,1,3) 2 [3] 2 [3] 2 = [3,3] | 24 | 4 | а 3 = 2 {3} 2 {3} 2 = {3,3} | 4 | 6 | {} | 4 | {3} | {3} | никто | Настоящий тетраэдр То же, что | ||
| Г 23 2 [3] 2 [5] 2 = [3,5] | 120 | 10 | 2 {3} 2 {5} 2 = {3,5} | 12 | 30 | {} | 20 | {3} | {5} | никто | Настоящий икосаэдр | ||
| 2 {5} 2 {3} 2 = {5,3} | 20 | 30 | {} | 12 | {5} | {3} | никто | Настоящий додекаэдр | |||||
| Г(2,1,3) 2 [3] 2 [4] 2 = [3,4] | 48 | 6 | б 2 3 = β 3 = {3,4} | 6 | 12 | {} | 8 | {3} | {4} | {4} | Настоящий октаэдр То же, что {}+{}+{}, порядок 8 То же, что | ||
| с 2 3 = γ 3 = {4,3} | 8 | 12 | {} | 6 | {4} | {3} | никто | Настоящий куб То же, что {}×{}×{} или | |||||
| Г(р,1,3) 2 [3] 2 [4] п р=2,3,4,... | 6 р. 3 | 33р | б п 3 = 2 {3} 2 {4} п | | 33р | 33р 2 | {} | п 3 | {3} | 2 {4} п | 2 {4} п | Обобщенный октаэдр То же, что p {}+ p {}+ p {}, порядок p 3 То же, что | |
| с п 3 = п {4} 2 {3} 2 | п 3 | 33р 2 | п {} | 33р | п {4} 2 | {3} | никто | Обобщенный куб То же, что p {}× p {}× p {} или | |||||
| Г(3,1,3) 2 [3] 2 [4] 3 | 162 | 9 | б 3 3 = 2 {3} 2 {4} 3 | 9 | 27 | {} | 27 | {3} | 2 {4} 3 | 2 {4} 3 | То же, что 3 {}+ 3 {}+ 3 {}, порядок 27. То же, что | ||
| с 3 3 = 3 {4} 2 {3} 2 | 27 | 27 | 3 {} | 9 | 3 {4} 2 | {3} | никто | То же, что 3 {}× 3 {}× 3 {} или | |||||
| Г(4,1,3) 2 [3] 2 [4] 4 | 384 | 12 | б 4 3 = 2 {3} 2 {4} 4 | 12 | 48 | {} | 64 | {3} | 2 {4} 4 | 2 {4} 4 | То же, что 4 {}+ 4 {}+ 4 {}, порядок 64. То же, что | ||
| с 4 3 = 4 {4} 2 {3} 2 | 64 | 48 | 4 {} | 12 | 4 {4} 2 | {3} | никто | То же, что 4 {}× 4 {}× 4 {} или | |||||
| Г(5,1,3) 2 [3] 2 [4] 5 | 750 | 15 | б 5 3 = 2 {3} 2 {4} 5 | 15 | 75 | {} | 125 | {3} | 2 {4} 5 | 2 {4} 5 | То же, что 5 {}+ 5 {}+ 5 {}, порядок 125. То же, что | ||
| с 5 3 = 5 {4} 2 {3} 2 | 125 | 75 | 5 {} | 15 | 5 {4} 2 | {3} | никто | То же, что 5 {}× 5 {}× 5 {} или | |||||
| Г(6,1,3) 2 [3] 2 [4] 6 | 1296 | 18 | б 6 3 = 2 {3} 2 {4} 6 | 36 | 108 | {} | 216 | {3} | 2 {4} 6 | 2 {4} 6 | То же, что 6 {}+ 6 {}+ 6 {}, порядок 216. То же, что | ||
| с 6 3 = 6 {4} 2 {3} 2 | 216 | 108 | 6 {} | 18 | 6 {4} 2 | {3} | никто | То же, что 6 {}× 6 {}× 6 {} или | |||||
| Г 25 3 [3] 3 [3] 3 | 648 | 9 | 3 {3} 3 {3} 3 | 27 | 72 | 3 {} | 27 | 3 {3} 3 | 3 {3} 3 | 3 {4} 2 | То же, что представление как 2 21 Гессенский многогранник | ||
| Г 26 2 [4] 3 [3] 3 | 1296 | 18 | 2 {4} 3 {3} 3 | 54 | 216 | {} | 72 | 2 {4} 3 | 3 {3} 3 | {6} | |||
| 3 {3} 3 {4} 2 | 72 | 216 | 3 {} | 54 | 3 {3} 3 | 3 {4} 2 | 3 {4} 3 | То же, что представление как 1 22 | |||||
Визуализации правильных комплексных многогранников
[ редактировать ]- 2D ортогональные проекции комплексных многогранников, p { s } t { r } r
- 3 {3} 3 {3} 3 ,




 или
или 



 , имеет 27 вершин, 72 трёхребра и 27 граней, одна из которых выделена синим цветом. [25]
, имеет 27 вершин, 72 трёхребра и 27 граней, одна из которых выделена синим цветом. [25] - 2 {4} 3 {3} 3 ,




 имеет 54 вершины, 216 простых ребер и 72 грани, одна грань выделена синим цветом. [26]
имеет 54 вершины, 216 простых ребер и 72 грани, одна грань выделена синим цветом. [26] - 3 {3} 3 {4} 2 ,




 или
или 



 , имеет 72 вершины, 216 трёхрёбер и 54 вершины, одна грань выделена синим цветом. [27]
, имеет 72 вершины, 216 трёхрёбер и 54 вершины, одна грань выделена синим цветом. [27]
- Обобщенные октаэдры
Обобщенные октаэдры имеют правильную конструкцию: ![]()
![]()
![]()
![]()
![]() и квазирегулярную форму как
и квазирегулярную форму как ![]()
![]()
![]()
![]() . Все элементы являются симплексами .
. Все элементы являются симплексами .
- 2 {3} 2 {4} 3 ,




 или
или 

 , с 9 вершинами, 27 ребрами и 27 гранями
, с 9 вершинами, 27 ребрами и 27 гранями - 2 {3} 2 {4} 4 ,




 или
или 


 , с 12 вершинами, 48 ребрами и 64 гранями.
, с 12 вершинами, 48 ребрами и 64 гранями. - 2 {3} 2 {4} 5 ,




 или
или 


 , с 15 вершинами, 75 ребрами и 125 гранями.
, с 15 вершинами, 75 ребрами и 125 гранями. - 2 {3} 2 {4} 6 ,




 или
или 


 , с 18 вершинами, 108 ребрами и 216 гранями.
, с 18 вершинами, 108 ребрами и 216 гранями. - 2 {3} 2 {4} 7 ,




 или
или 


 , с 21 вершиной, 147 ребрами и 343 гранями.
, с 21 вершиной, 147 ребрами и 343 гранями. - 2 {3} 2 {4} 8 ,




 или
или 


 , с 24 вершинами, 192 ребрами и 512 гранями.
, с 24 вершинами, 192 ребрами и 512 гранями. - 2 {3} 2 {4} 9 ,




 или
или 


 , с 27 вершинами, 243 ребрами и 729 гранями.
, с 27 вершинами, 243 ребрами и 729 гранями. - 2 {3} 2 {4} 10 ,




 или
или 



 , с 30 вершинами, 300 ребрами и 1000 гранями.
, с 30 вершинами, 300 ребрами и 1000 гранями.
- Обобщенные кубы
Обобщенные кубы имеют правильную конструкцию: ![]()
![]()
![]()
![]()
![]() и призматическая конструкция, как
и призматическая конструкция, как ![]()
![]()
![]()
![]()
![]() , произведение трех p -угольных 1-многогранников. Элементы представляют собой обобщенные кубы меньшей размерности.
, произведение трех p -угольных 1-многогранников. Элементы представляют собой обобщенные кубы меньшей размерности.
- 4 {4} 2 {3} 2 ,




 или
или 



 , с 64 вершинами, 48 ребрами и 12 гранями.
, с 64 вершинами, 48 ребрами и 12 гранями. - 5 {4} 2 {3} 2 ,




 или
или 



 , со 125 вершинами, 75 ребрами и 15 гранями.
, со 125 вершинами, 75 ребрами и 15 гранями. - 6 {4} 2 {3} 2 ,




 или
или 



 , с 216 вершинами, 108 ребрами и 18 гранями.
, с 216 вершинами, 108 ребрами и 18 гранями. - 7 {4} 2 {3} 2 ,




 или
или 



 , с 343 вершинами, 147 ребрами и 21 гранью.
, с 343 вершинами, 147 ребрами и 21 гранью. - 8 {4} 2 {3} 2 ,




 или
или 



 , с 512 вершинами, 192 ребрами и 24 гранями.
, с 512 вершинами, 192 ребрами и 24 гранями. - 9 {4} 2 {3} 2 ,




 или
или 



 , с 729 вершинами, 243 ребрами и 27 гранями.
, с 729 вершинами, 243 ребрами и 27 гранями. - 10 {4} 2 {3} 2 ,




 или
или 



 , с 1000 вершинами, 300 ребрами и 30 гранями
, с 1000 вершинами, 300 ребрами и 30 гранями
Перечисление правильных комплексных 4-многогранников
[ редактировать ]Коксетер перечислил этот список незвездных правильных комплексных 4-многогранников в , включая 6 выпуклых правильных 4-многогранников в . [23]
| Космос | Группа | Заказ | Коксетер число | Многогранник | Вершины | Края | Лица | Клетки | Ван Ус многоугольник | Примечания |
|---|---|---|---|---|---|---|---|---|---|---|
| Г(1,1,4) 2 [3] 2 [3] 2 [3] 2 = [3,3,3] | 120 | 5 | а 4 = 2 {3} 2 {3} 2 {3} 2 = {3,3,3} | 5 | 10 {} | 10 {3} | 5 {3,3} | никто | Настоящий 5-клеточный (симплекс) | |
| Г 28 2 [3] 2 [4] 2 [3] 2 = [3,4,3] | 1152 | 12 | 2 {3} 2 {4} 2 {3} 2 = {3,4,3} | 24 | 96 {} | 96 {3} | 24 {3,4} | {6} | Настоящий 24-клеточный | |
| Г 30 2 [3] 2 [3] 2 [5] 2 = [3,3,5] | 14400 | 30 | 2 {3} 2 {3} 2 {5} 2 = {3,3,5} | 120 | 720 {} | 1200 {3} | 600 {3,3} | {10} | Настоящий 600-ячеечный | |
| 2 {5} 2 {3} 2 {3} 2 = {5,3,3} | 600 | 1200 {} | 720 {5} | 120 {5,3} | Настоящий 120-ячеечный | |||||
| Г(2,1,4) 2 [3] 2 [3] 2 [4] п =[3,3,4] | 384 | 8 | б 2 4 = б 4 = {3,3,4} | 8 | 24 {} | 32 {3} | 16 {3,3} | {4} | Настоящий 16-клеточный То же, что | |
| с 2 4 = γ 4 = {4,3,3} | 16 | 32 {} | 24 {4} | 8 {4,3} | никто | Настоящий тессеракт То же, что {} 4 или | ||||
| Г(р,1,4) 2 [3] 2 [3] 2 [4] п р=2,3,4,... | 24 р. 4 | 4 р. | б п 4 = 2 {3} 2 {3} 2 {4} п | 4 р. | 6 р. 2 {} | 4 р. 3 {3} | п 4 {3,3} | 2 {4} п | Обобщенный 4- ортоплекс То же, что | |
| с п 4 = п {4} 2 {3} 2 {3} 2 | п 4 | 4 р. 3 п {} | 6 р. 2 п {4} 2 | 4 р. п {4} 2 {3} 2 | никто | Обобщенный тессеракт То же, что и п {} 4 или | ||||
| Г(3,1,4) 2 [3] 2 [3] 2 [4] 3 | 1944 | 12 | б 3 4 = 2 {3} 2 {3} 2 {4} 3 | 12 | 54 {} | 108 {3} | 81 {3,3} | 2 {4} 3 | Обобщенный 4- ортоплекс То же, что | |
| с 3 4 = 3 {4} 2 {3} 2 {3} 2 | 81 | 108 3 {} | 54 3 {4} 2 | 12 3 {4} 2 {3} 2 | никто | То же, что 3 {} 4 или | ||||
| Г(4,1,4) 2 [3] 2 [3] 2 [4] 4 | 6144 | 16 | б 4 4 = 2 {3} 2 {3} 2 {4} 4 | 16 | 96 {} | 256 {3} | 64 {3,3} | 2 {4} 4 | То же, что | |
| с 4 4 = 4 {4} 2 {3} 2 {3} 2 | 256 | 256 4 {} | 96 4 {4} 2 | 16 4 {4} 2 {3} 2 | никто | То же, что и 4 {} 4 или | ||||
| Г(5,1,4) 2 [3] 2 [3] 2 [4] 5 | 15000 | 20 | б 5 4 = 2 {3} 2 {3} 2 {4} 5 | 20 | 150 {} | 500 {3} | 625 {3,3} | 2 {4} 5 | То же, что | |
| с 5 4 = 5 {4} 2 {3} 2 {3} 2 | 625 | 500 5 {} | 150 5 {4} 2 | 20 5 {4} 2 {3} 2 | никто | То же, что 5 {} 4 или | ||||
| Г(6,1,4) 2 [3] 2 [3] 2 [4] 6 | 31104 | 24 | б 6 4 = 2 {3} 2 {3} 2 {4} 6 | 24 | 216 {} | 864 {3} | 1296 {3,3} | 2 {4} 6 | То же, что | |
| с 6 4 = 6 {4} 2 {3} 2 {3} 2 | 1296 | 864 6 {} | 216 6 {4} 2 | 24 6 {4} 2 {3} 2 | никто | То же, что и 6 {} 4 или | ||||
| Г 32 3 [3] 3 [3] 3 [3] 3 | 155520 | 30 | 3 {3} 3 {3} 3 {3} 3 | 240 | 2160 3 {} | 2160 3 {3} 3 | 240 3 {3} 3 {3} 3 | 3 {4} 3 | Сознательный многогранник представление как 4 21 |
Визуализации правильных комплексных 4-многогранников
[ редактировать ]- Действительное {3,3,3} ,






 , имел 5 вершин, 10 ребер, 10 граней {3} и 5 ячеек {3,3}
, имел 5 вершин, 10 ребер, 10 граней {3} и 5 ячеек {3,3} - Действительное {3,4,3} ,






 , имел 24 вершины, 96 ребер, 96 граней {3} и 24 ячейки {3,4}.
, имел 24 вершины, 96 ребер, 96 граней {3} и 24 ячейки {3,4}. - Действительное {5,3,3} ,






 , имел 600 вершин, 1200 ребер, 720 граней {5} и 120 ячеек {5,3}.
, имел 600 вершин, 1200 ребер, 720 граней {5} и 120 ячеек {5,3}. - Действительное {3,3,5} ,






 , имел 120 вершин, 720 ребер, 1200 граней {3} и 600 ячеек {3,3}.
, имел 120 вершин, 720 ребер, 1200 граней {3} и 600 ячеек {3,3}. - Соображая многогранник ,






 , имеет 240 вершин, 2160 3-ребер, 2160 3{3}3 грани и 240 3{3}3{3}3 ячеек.
, имеет 240 вершин, 2160 3-ребер, 2160 3{3}3 грани и 240 3{3}3{3}3 ячеек.
- Обобщенные 4-ортоплексы
Обобщенные 4-ортоплексы имеют правильную конструкцию: ![]()
![]()
![]()
![]()
![]()
![]()
![]() и квазирегулярную форму как
и квазирегулярную форму как ![]()
![]()
![]()
![]()
![]()
![]() . Все элементы являются симплексами .
. Все элементы являются симплексами .
- 2 {3} 2 {3} 2 {4} 3 ,






 или
или 



 , с 12 вершинами, 54 ребрами, 108 гранями и 81 ячейкой.
, с 12 вершинами, 54 ребрами, 108 гранями и 81 ячейкой. - 2 {3} 2 {3} 2 {4} 4 ,






 или
или 




 , с 16 вершинами, 96 ребрами, 256 гранями и 256 ячейками.
, с 16 вершинами, 96 ребрами, 256 гранями и 256 ячейками. - 2 {3} 2 {3} 2 {4} 5 ,






 или
или 




 , с 20 вершинами, 150 ребрами, 500 гранями и 625 ячейками.
, с 20 вершинами, 150 ребрами, 500 гранями и 625 ячейками. - 2 {3} 2 {3} 2 {4} 6 ,






 или
или 




 , с 24 вершинами, 216 ребрами, 864 гранями и 1296 ячейками.
, с 24 вершинами, 216 ребрами, 864 гранями и 1296 ячейками. - 2 {3} 2 {3} 2 {4} 7 ,






 или
или 




 , с 28 вершинами, 294 ребрами, 1372 гранями и 2401 ячейкой.
, с 28 вершинами, 294 ребрами, 1372 гранями и 2401 ячейкой. - 2 {3} 2 {3} 2 {4} 8 ,






 или
или 




 , с 32 вершинами, 384 ребрами, 2048 гранями и 4096 ячейками.
, с 32 вершинами, 384 ребрами, 2048 гранями и 4096 ячейками. - 2 {3} 2 {3} 2 {4} 9 ,






 или
или 




 , с 36 вершинами, 486 ребрами, 2916 гранями и 6561 ячейкой.
, с 36 вершинами, 486 ребрами, 2916 гранями и 6561 ячейкой. - 2 {3} 2 {3} 2 {4} 10 ,






 или
или 





 , с 40 вершинами, 600 ребрами, 4000 гранями и 10000 ячейками.
, с 40 вершинами, 600 ребрами, 4000 гранями и 10000 ячейками.
- Обобщенные 4-кубы
Обобщенные тессеракты имеют правильную конструкцию: ![]()
![]()
![]()
![]()
![]()
![]()
![]() и призматическая конструкция, как
и призматическая конструкция, как ![]()
![]()
![]()
![]()
![]()
![]()
![]() , произведение четырех p -угольных 1-многогранников. Элементы представляют собой обобщенные кубы меньшей размерности.
, произведение четырех p -угольных 1-многогранников. Элементы представляют собой обобщенные кубы меньшей размерности.
- 3 {4} 2 {3} 2 {3} 2 ,






 или
или 





 , с 81 вершиной, 108 ребрами, 54 гранями и 12 ячейками.
, с 81 вершиной, 108 ребрами, 54 гранями и 12 ячейками. - 4 {4} 2 {3} 2 {3} 2 ,






 или
или 





 , с 256 вершинами, 96 ребрами, 96 гранями и 16 ячейками.
, с 256 вершинами, 96 ребрами, 96 гранями и 16 ячейками. - 5 {4} 2 {3} 2 {3} 2 ,






 или
или 





 , с 625 вершинами, 500 ребрами, 150 гранями и 20 ячейками.
, с 625 вершинами, 500 ребрами, 150 гранями и 20 ячейками. - 6 {4} 2 {3} 2 {3} 2 ,






 или
или 





 , с 1296 вершинами, 864 ребрами, 216 гранями и 24 ячейками.
, с 1296 вершинами, 864 ребрами, 216 гранями и 24 ячейками. - 7 {4} 2 {3} 2 {3} 2 ,






 или
или 





 , с 2401 вершиной, 1372 ребрами, 294 гранями и 28 ячейками.
, с 2401 вершиной, 1372 ребрами, 294 гранями и 28 ячейками. - 8 {4} 2 {3} 2 {3} 2 ,






 или
или 





 , с 4096 вершинами, 2048 ребрами, 384 гранями и 32 ячейками.
, с 4096 вершинами, 2048 ребрами, 384 гранями и 32 ячейками. - 9 {4} 2 {3} 2 {3} 2 ,






 или
или 





 , с 6561 вершиной, 2916 ребрами, 486 гранями и 36 ячейками.
, с 6561 вершиной, 2916 ребрами, 486 гранями и 36 ячейками. - 10 {4} 2 {3} 2 {3} 2 ,






 или
или 





 , с 10000 вершинами, 4000 ребрами, 600 гранями и 40 ячейками.
, с 10000 вершинами, 4000 ребрами, 600 гранями и 40 ячейками.
Перечисление правильных комплексных 5-многогранников
[ редактировать ]Правильные комплексные 5-многогранники в или выше существуют в трех семействах: действительные симплексы , обобщенный гиперкуб и ортоплекс .
| Космос | Группа | Заказ | Многогранник | Вершины | Края | Лица | Клетки | 4-ликий | Ван Ус многоугольник | Примечания |
|---|---|---|---|---|---|---|---|---|---|---|
| Г(1,1,5) = [3,3,3,3] | 720 | а 5 = {3,3,3,3} | 6 | 15 {} | 20 {3} | 15 {3,3} | 6 {3,3,3} | никто | Настоящий 5-симплекс | |
| Г(2,1,5) =[3,3,3,4] | 3840 | б 2 5 = β 5 = {3,3,3,4} | 10 | 40 {} | 80 {3} | 80 {3,3} | 32 {3,3,3} | {4} | Настоящий 5-ортоплекс То же, что | |
| с 2 5 = γ 5 = {4,3,3,3} | 32 | 80 {} | 80 {4} | 40 {4,3} | 10 {4,3,3} | никто | Настоящий 5-куб То же, что {} 5 или | |||
| Г(р,1,5) 2 [3] 2 [3] 2 [3] 2 [4] п | 120 р. 5 | б п 5 = 2 {3} 2 {3} 2 {3} 2 {4} п | 5 р. | 10 р. 2 {} | 10 р. 3 {3} | 5 р. 4 {3,3} | п 5 {3,3,3} | 2 {4} п | Обобщенный 5-ортоплекс То же, что | |
| с п 5 = п {4} 2 {3} 2 {3} 2 {3} 2 | п 5 | 5 р. 4 п {} | 10 р. 3 п {4} 2 | 10 р. 2 п {4} 2 {3} 2 | 5 р. п {4} 2 {3} 2 {3} 2 | никто | Обобщенный 5-куб То же, что и п {} 5 или | |||
| Г(3,1,5) 2 [3] 2 [3] 2 [3] 2 [4] 3 | 29160 | б 3 5 = 2 {3} 2 {3} 2 {3} 2 {4} 3 | 15 | 90 {} | 270 {3} | 405 {3,3} | 243 {3,3,3} | 2 {4} 3 | То же, что | |
| с 3 5 = 3 {4} 2 {3} 2 {3} 2 {3} 2 | 243 | 405 3 {} | 270 3 {4} 2 | 90 3 {4} 2 {3} 2 | 15 3 {4} 2 {3} 2 {3} 2 | никто | То же, что 3 {} 5 или | |||
| Г(4,1,5) 2 [3] 2 [3] 2 [3] 2 [4] 4 | 122880 | б 4 5 = 2 {3} 2 {3} 2 {3} 2 {4} 4 | 20 | 160 {} | 640 {3} | 1280 {3,3} | 1024 {3,3,3} | 2 {4} 4 | То же, что | |
| с 4 5 = 4 {4} 2 {3} 2 {3} 2 {3} 2 | 1024 | 1280 4 {} | 640 4 {4} 2 | 160 4 {4} 2 {3} 2 | 20 4 {4} 2 {3} 2 {3} 2 | никто | То же, что и 4 {} 5 или | |||
| Г(5,1,5) 2 [3] 2 [3] 2 [3] 2 [4] 5 | 375000 | б 5 5 = 2 {3} 2 {3} 2 {3} 2 {5} 5 | 25 | 250 {} | 1250 {3} | 3125 {3,3} | 3125 {3,3,3} | 2 {5} 5 | То же, что | |
| с 5 5 = 5 {4} 2 {3} 2 {3} 2 {3} 2 | 3125 | 3125 5 {} | 1250 5 {5} 2 | 250 5 {5} 2 {3} 2 | 25 5 {4} 2 {3} 2 {3} 2 | никто | То же, что 5 {} 5 или | |||
| Г(6,1,5) 2 [3] 2 [3] 2 [3] 2 [4] 6 | 933210 | б 6 5 = 2 {3} 2 {3} 2 {3} 2 {4} 6 | 30 | 360 {} | 2160 {3} | 6480 {3,3} | 7776 {3,3,3} | 2 {4} 6 | То же, что | |
| с 6 5 = 6 {4} 2 {3} 2 {3} 2 {3} 2 | 7776 | 6480 6 {} | 2160 6 {4} 2 | 360 6 {4} 2 {3} 2 | 30 6 {4} 2 {3} 2 {3} 2 | никто | То же, что и 6 {} 5 или |
Визуализации правильных комплексных 5-многогранников
[ редактировать ]- Обобщенные 5-ортоплексы
Обобщенные 5-ортоплексы имеют правильную конструкцию: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() и квазирегулярную форму как
и квазирегулярную форму как ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Все элементы являются симплексами .
. Все элементы являются симплексами .
- Действительное {3,3,3,4} ,








 , с 10 вершинами, 40 ребрами, 80 гранями, 80 ячейками и 32 4-гранями
, с 10 вершинами, 40 ребрами, 80 гранями, 80 ячейками и 32 4-гранями - 2 {3} 2 {3} 2 {3} 2 {4} 3 ,








 , с 15 вершинами, 90 ребрами, 270 гранями, 405 ячейками и 243 4-гранями.
, с 15 вершинами, 90 ребрами, 270 гранями, 405 ячейками и 243 4-гранями. - 2 {3} 2 {3} 2 {3} 2 {4} 4 ,








 , с 20 вершинами, 160 ребрами, 640 гранями, 1280 ячейками и 1024 4-гранями.
, с 20 вершинами, 160 ребрами, 640 гранями, 1280 ячейками и 1024 4-гранями. - 2 {3} 2 {3} 2 {3} 2 {4} 5 ,








 , с 25 вершинами, 250 ребрами, 1250 гранями, 3125 ячейками и 3125 4-гранями.
, с 25 вершинами, 250 ребрами, 1250 гранями, 3125 ячейками и 3125 4-гранями. - 2 {3} 2 {3} 2 {3} 2 {4} 6 ,








 , с 30 вершинами, 360 ребрами, 2160 гранями, 6480 ячейками, 7776 4-гранями
, с 30 вершинами, 360 ребрами, 2160 гранями, 6480 ячейками, 7776 4-гранями - 2 {3} 2 {3} 2 {3} 2 {4} 7 ,








 , с 35 вершинами, 490 ребрами, 3430 гранями, 12005 ячеек, 16807 4-гранями
, с 35 вершинами, 490 ребрами, 3430 гранями, 12005 ячеек, 16807 4-гранями - 2 {3} 2 {3} 2 {3} 2 {4} 8 ,








 , с 40 вершинами, 640 ребрами, 5120 гранями, 20480 ячейками, 32768 4-гранями
, с 40 вершинами, 640 ребрами, 5120 гранями, 20480 ячейками, 32768 4-гранями - 2 {3} 2 {3} 2 {3} 2 {4} 9 ,








 , с 45 вершинами, 810 ребрами, 7290 гранями, 32805 ячейками, 59049 4-гранями
, с 45 вершинами, 810 ребрами, 7290 гранями, 32805 ячейками, 59049 4-гранями - 2 {3} 2 {3} 2 {3} 2 {4} 10 ,








 , с 50 вершинами, 1000 ребрами, 10000 гранями, 50000 ячейками, 100000 4-гранями
, с 50 вершинами, 1000 ребрами, 10000 гранями, 50000 ячейками, 100000 4-гранями
- Обобщенные 5-кубы
Обобщенные 5-кубы имеют правильную конструкцию: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() и призматическая конструкция, как
и призматическая конструкция, как ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , произведение пяти p -угольных 1-многогранников. Элементы представляют собой обобщенные кубы меньшей размерности.
, произведение пяти p -угольных 1-многогранников. Элементы представляют собой обобщенные кубы меньшей размерности.
- Действительное {4,3,3,3} ,








 , с 32 вершинами, 80 ребрами, 80 гранями, 40 ячейками и 10 4-гранями.
, с 32 вершинами, 80 ребрами, 80 гранями, 40 ячейками и 10 4-гранями. - 3 {4} 2 {3} 2 {3} 2 {3} 2 ,








 , с 243 вершинами, 405 ребрами, 270 гранями, 90 ячейками и 15 4-гранями.
, с 243 вершинами, 405 ребрами, 270 гранями, 90 ячейками и 15 4-гранями. - 4 {4} 2 {3} 2 {3} 2 {3} 2 ,








 , с 1024 вершинами, 1280 ребрами, 640 гранями, 160 ячейками и 20 4-гранями.
, с 1024 вершинами, 1280 ребрами, 640 гранями, 160 ячейками и 20 4-гранями. - 5 {4} 2 {3} 2 {3} 2 {3} 2 ,








 , с 3125 вершинами, 3125 ребрами, 1250 гранями, 250 ячейками и 25 4-гранями.
, с 3125 вершинами, 3125 ребрами, 1250 гранями, 250 ячейками и 25 4-гранями. - 6 {4} 2 {3} 2 {3} 2 {3} 2 ,








 , с 7776 вершинами, 6480 ребрами, 2160 гранями, 360 ячейками и 30 4-гранями.
, с 7776 вершинами, 6480 ребрами, 2160 гранями, 360 ячейками и 30 4-гранями.
Перечисление правильных комплексных 6-многогранников
[ редактировать ]| Космос | Группа | Заказ | Многогранник | Вершины | Края | Лица | Клетки | 4-ликий | 5-гранный | Ван Ус многоугольник | Примечания |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Г(1,1,6) = [3,3,3,3,3] | 720 | а 6 = {3,3,3,3,3} | 7 | 21 {} | 35 {3} | 35 {3,3} | 21 {3,3,3} | 7 {3,3,3,3} | никто | Настоящий 6-симплекс | |
| Г(2,1,6) [3,3,3,4] | 46080 | б 2 6 = б 6 = {3,3,3,4} | 12 | 60 {} | 160 {3} | 240 {3,3} | 192 {3,3,3} | 64 {3,3,3,3} | {4} | Настоящий 6-ортоплекс То же, что | |
| с 2 6 = γ 6 = {4,3,3,3} | 64 | 192 {} | 240 {4} | 160 {4,3} | 60 {4,3,3} | 12 {4,3,3,3} | никто | Настоящий 6-куб То же, что {} 6 или | |||
| Г(р,1,6) 2 [3] 2 [3] 2 [3] 2 [4] п | 720 р. 6 | б п 6 = 2 {3} 2 {3} 2 {3} 2 {4} п | 6 р. | 15 р. 2 {} | 20 р. 3 {3} | 15 р. 4 {3,3} | 6 р. 5 {3,3,3} | п 6 {3,3,3,3} | 2 {4} п | Обобщенный 6-ортоплекс То же, что | |
| с п 6 = п {4} 2 {3} 2 {3} 2 {3} 2 | п 6 | 6 р. 5 п {} | 15 р. 4 п {4} 2 | 20 р. 3 п {4} 2 {3} 2 | 15 р. 2 п {4} 2 {3} 2 {3} 2 | 6 р. п {4} 2 {3} 2 {3} 2 {3} 2 | никто | Обобщенный 6-куб То же, что и п {} 6 или |
Визуализации правильных комплексных 6-многогранников
[ редактировать ]- Обобщенные 6-ортоплексы
Обобщенные 6-ортоплексы имеют правильную конструкцию: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() и квазирегулярную форму как
и квазирегулярную форму как ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Все элементы являются симплексами .
. Все элементы являются симплексами .
- Действительное {3,3,3,3,4} ,










 , с 12 вершинами, 60 ребрами, 160 гранями, 240 ячейками, 192 4-гранями и 64 5-гранями.
, с 12 вершинами, 60 ребрами, 160 гранями, 240 ячейками, 192 4-гранями и 64 5-гранями. - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 3 ,










 , с 18 вершинами, 135 ребрами, 540 гранями, 1215 ячейками, 1458 4-гранями и 729 5-гранями.
, с 18 вершинами, 135 ребрами, 540 гранями, 1215 ячейками, 1458 4-гранями и 729 5-гранями. - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 4 ,










 , с 24 вершинами, 240 ребрами, 1280 гранями, 3840 ячейками, 6144 4-гранями и 4096 5-гранями.
, с 24 вершинами, 240 ребрами, 1280 гранями, 3840 ячейками, 6144 4-гранями и 4096 5-гранями. - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 5 ,










 , с 30 вершинами, 375 ребрами, 2500 гранями, 9375 ячейками, 18750 4-гранями и 15625 5-гранями.
, с 30 вершинами, 375 ребрами, 2500 гранями, 9375 ячейками, 18750 4-гранями и 15625 5-гранями. - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 6 ,










 , с 36 вершинами, 540 ребрами, 4320 гранями, 19 440 ячейками, 46 656 4-гранями и 46 656 5-гранями.
, с 36 вершинами, 540 ребрами, 4320 гранями, 19 440 ячейками, 46 656 4-гранями и 46 656 5-гранями. - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 7 ,










 , с 42 вершинами, 735 ребрами, 6860 гранями, 36015 ячейками, 100842 4-гранниками, 117649 5-гранниками
, с 42 вершинами, 735 ребрами, 6860 гранями, 36015 ячейками, 100842 4-гранниками, 117649 5-гранниками - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 8 ,










 , с 48 вершинами, 960 ребрами, 10240 гранями, 61440 ячейками, 196608 4-гранниками, 262144 5-гранниками
, с 48 вершинами, 960 ребрами, 10240 гранями, 61440 ячейками, 196608 4-гранниками, 262144 5-гранниками - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 9 ,










 , с 54 вершинами, 1215 ребрами, 14580 гранями, 98415 ячейками, 354294 4-гранями, 531441 5-гранями
, с 54 вершинами, 1215 ребрами, 14580 гранями, 98415 ячейками, 354294 4-гранями, 531441 5-гранями - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 10 ,










 , с 60 вершинами, 1500 ребрами, 20000 граней, 150000 ячеек, 600000 4-граней, 1000000 5-граней
, с 60 вершинами, 1500 ребрами, 20000 граней, 150000 ячеек, 600000 4-граней, 1000000 5-граней
- Обобщенные 6-кубы
Обобщенные 6-кубы имеют правильную конструкцию: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() и призматическая конструкция, как
и призматическая конструкция, как ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , произведение шести p -угольных 1-многогранников. Элементы представляют собой обобщенные кубы меньшей размерности.
, произведение шести p -угольных 1-многогранников. Элементы представляют собой обобщенные кубы меньшей размерности.
- Действительное {3,3,3,3,3,4} ,










 , с 64 вершинами, 192 ребрами, 240 гранями, 160 ячейками, 60 4-гранями и 12 5-гранями.
, с 64 вершинами, 192 ребрами, 240 гранями, 160 ячейками, 60 4-гранями и 12 5-гранями. - 3 {4} 2 {3} 2 {3} 2 {3} 2 {3} 2 ,










 , с 729 вершинами, 1458 ребрами, 1215 гранями, 540 ячейками, 135 4-гранями и 18 5-гранями.
, с 729 вершинами, 1458 ребрами, 1215 гранями, 540 ячейками, 135 4-гранями и 18 5-гранями. - 4 {4} 2 {3} 2 {3} 2 {3} 2 {3} 2 ,










 , с 4096 вершинами, 6144 ребрами, 3840 гранями, 1280 ячейками, 240 4-гранями и 24 5-гранями.
, с 4096 вершинами, 6144 ребрами, 3840 гранями, 1280 ячейками, 240 4-гранями и 24 5-гранями. - 5 {4} 2 {3} 2 {3} 2 {3} 2 {3} 2 ,










 , с 15625 вершинами, 18750 ребрами, 9375 гранями, 2500 ячейками, 375 4-гранями и 30 5-гранями.
, с 15625 вершинами, 18750 ребрами, 9375 гранями, 2500 ячейками, 375 4-гранями и 30 5-гранями.
Перечисление правильных сложных апейротопов
[ редактировать ]Коксетер перечислил этот список незвездных правильных сложных апейротопов или сот. [28]
Для каждого измерения существует 12 апейротопов, обозначенных как δ. п , р
n+1 существует в любых измерениях , или если р = q =2. Коксетер называет эти обобщенные кубические соты для n >2. [29]
Каждый из них имеет пропорциональное количество элементов, заданное как:
- k-граней = , где и н ! обозначает факториал числа n .
Регулярные комплексные 1-многогранники
[ редактировать ]Единственный правильный комплексный 1-многогранник — это ∞ {}, или ![]() . Его реальным представлением является апейрогон , {∞} или
. Его реальным представлением является апейрогон , {∞} или ![]()
![]()
![]() .
.
Правильные сложные апейрогоны
[ редактировать ]




 представляет собой смесь двух правильных апейрогонов
представляет собой смесь двух правильных апейрогонов 

 и
и 

 , здесь видно с синими и розовыми краями.
, здесь видно с синими и розовыми краями. 

 имеет только один цвет ребер, поскольку q нечетно, что делает его двойным покрытием.
имеет только один цвет ребер, поскольку q нечетно, что делает его двойным покрытием. Комплексные апейрогоны ранга 2 обладают симметрией p [ q ] r , где 1/ p + 2/ q + 1/ r = 1. Коксетер выражает их как δ п , р
2 , где q ограничено так, чтобы удовлетворять q = 2/(1 – ( p + r )/ pr ) . [30]
Есть 8 решений:
| 2 [∞] 2 | 3 [12] 2 | 4 [8] 2 | 6 [6] 2 | 3 [6] 3 | 6 [4] 3 | 4 [4] 4 | 6 [3] 6 |
Имеются два исключенных решения нечетные q и неравные p и r : 10 [5] 2 и 12 [3] 4 , или ![]()
![]()
![]() и
и ![]()
![]()
![]() .
.
Правильный комплексный апейрогон p { q } r имеет p -ребра и r -угольные вершинные фигуры. Двойственный апейрогон к p { q } r — это r { q } p . Апейрогон вида p { q } p самодвойственный. Группы вида p [2 q ] 2 обладают полусимметрией p [ q ] p , поэтому правильный апейрогон ![]()
![]()
![]()
![]() то же самое, что и квазирегулярный
то же самое, что и квазирегулярный ![]()
![]()
![]() . [31]
. [31]
Апейрогоны могут быть представлены на плоскости Аргана с четырьмя различными расположениями вершин. Апейрогоны вида 2 { q } r имеют расположение вершин { q /2, p }. Форма p { q } 2 имеет расположение вершин как r { p , q /2}. Апейрогоны формы p {4} r имеют расположение вершин { p , r }.
Включая аффинные узлы и , существует еще 3 бесконечных решения: ∞ [2] ∞ , ∞ [4] 2 , ∞ [3] 3 и ![]()
![]()
![]() ,
, ![]()
![]()
![]() , и
, и ![]()
![]()
![]() . Первая является подгруппой индекса 2 второй. Вершины этих апейрогонов существуют в .
. Первая является подгруппой индекса 2 второй. Вершины этих апейрогонов существуют в .
| Космос | Группа | Апейрогон | Край | представитель. [32] | Картина | Примечания | |
|---|---|---|---|---|---|---|---|
| 2 [∞] 2 = [∞] | д 2,2 2 = {∞} | | {} | Настоящий апейрогон То же, что | |||
| / | ∞ [4] 2 | ∞ {4} 2 | ∞ {} | {4,4} |  | То же, что  | |
| ∞ [3] 3 | ∞ {3} 3 | ∞ {} | {3,6} | То же, что | |||
| п [ q ] р | д п, р 2 = п { q } р | п {} | |||||
| 3 [12] 2 | д 3,2 2 = 3 {12} 2 | 3 {} | г{3,6} |  | То же, что  | ||
| д 2,3 2 = 2 {12} 3 | {} | {6,3} |  | ||||
| 3 [6] 3 | д 3,3 2 = 3 {6} 3 | 3 {} | {3,6} | То же, что | |||
| 4 [8] 2 | д 4,2 2 = 4 {8} 2 | 4 {} | {4,4} |  | То же, что  | ||
| д 2,4 2 = 2 {8} 4 | {} | {4,4} |  | ||||
| 4 [4] 4 | д 4,4 2 = 4 {4} 4 | 4 {} | {4,4} |  | То же, что | ||
| 6 [6] 2 | д 6,2 2 = 6 {6} 2 | 6 {} | г{3,6} | То же, что | |||
| д 2,6 2 = 2 {6} 6 | {} | {3,6} | |||||
| 6 [4] 3 | д 6,3 2 = 6 {4} 3 | 6 {} | {6,3} |  | |||
| д 3,6 2 = 3 {4} 6 | 3 {} | {3,6} | |||||
| 6 [3] 6 | д 6,6 2 = 6 {3} 6 | 6 {} | {3,6} |  | То же, что | ||
Правильные сложные апейроэдры
[ редактировать ]Имеется 22 правильных комплексных апейроэдра вида p { a } q { b } r . 8 самодуальны ( p = r и a = b ), а 14 существуют как двойственные пары многогранников. Три из них вполне реальны ( p = q = r =2).
Коксетер символизирует 12 из них как δ. п , р
3 или p {4} 2 {4} r — правильная форма произведения апейротопа δ п , р
2 × д п , р
2 или p { q } r × p { q } r , где q определяется из p и r .
![]()
![]()
![]()
![]()
![]() то же самое, что
то же самое, что ![]()
![]()
![]()
![]() , а также
, а также ![]()
![]()
![]()
![]()
![]()
![]()
![]() , для p , r =2,3,4,6. Также
, для p , r =2,3,4,6. Также ![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]() . [33]
. [33]
| Космос | Группа | Апейроэдр | Вертекс | Край | Лицо | привык к нам апейрогон | Примечания | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 [3] 2 [4] ∞ | ∞ {4} 2 {3} 2 | ∞ {} | ∞ {4} 2 | То же, что ∞ {}× ∞ {}× ∞ {} или Реальное представление {4,3,4} | ||||||
| п [4] 2 [4] р | п {4} 2 {4} р | | п 2 | 2 пр | п {} | р 2 | п {4} 2 | 2 { q } р | То же, что | |
| [4,4] | д 2,2 3 = {4,4} | 4 | 8 | {} | 4 | {4} | {∞} | Настоящая квадратная плитка То же, что | ||
| 3 [4] 2 [4] 2 3 [4] 2 [4] 3 4 [4] 2 [4] 2 4 [4] 2 [4] 4 6 [4] 2 [4] 2 6 [4] 2 [4] 3 6 [4] 2 [4] 6 | 3 {4} 2 {4} 2 2 {4} 2 {4} 3 3 {4} 2 {4} 3 4 {4} 2 {4} 2 2 {4} 2 {4} 4 4 {4} 2 {4} 4 6 {4} 2 {4} 2 2 {4} 2 {4} 6 6 {4} 2 {4} 3 3 {4} 2 {4} 6 6 {4} 2 {4} 6 | 9 4 9 16 4 16 36 4 36 9 36 | 12 12 18 16 16 32 24 24 36 36 72 | 3 {} {} 3 {} 4 {} {} 4 {} 6 {} {} 6 {} 3 {} 6 {} | 4 9 9 4 16 16 4 36 9 36 36 | 3 {4} 2 {4} 3 {4} 2 4 {4} 2 {4} 4 {4} 2 6 {4} 2 {4} 6 {4} 2 3 {4} 2 6 {4} 2 | п { q } р | То же, что То же, что То же, что То же, что То же, что То же, что То же, что То же, что То же, что То же, что То же, что | ||
| Космос | Группа | Апейроэдр | Вертекс | Край | Лицо | привык к нам апейрогон | Примечания | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 [4] р [4] 2 | 2 {4} р {4} 2 | | 2 | {} | 2 | п {4} 2' | 2 {4} р | То же, что | ||
| [4,4] | {4,4} | 2 | 4 | {} | 2 | {4} | {∞} | То же, что | ||
| 2 [4] 3 [4] 2 2 [4] 4 [4] 2 2 [4] 6 [4] 2 | 2 {4} 3 {4} 2 2 {4} 4 {4} 2 2 {4} 6 {4} 2 | 2 | 9 16 36 | {} | 2 | 2 {4} 3 2 {4} 4 2 {4} 6 | 2 { q } р | То же, что То же, что То же, что | ||
| Космос | Группа | Апейроэдр | Вертекс | Край | Лицо | привык к нам апейрогон | Примечания | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 [6] 2 [3] 2 = [6,3] | {3,6} | | 1 | 3 | {} | 2 | {3} | {∞} | Настоящая треугольная плитка | |
| {6,3} | 2 | 3 | {} | 1 | {6} | никто | Настоящая шестиугольная плитка | |||
| 3 [4] 3 [3] 3 | 3 {3} 3 {4} 3 | 1 | 8 | 3 {} | 3 | 3 {3} 3 | 3 {4} 6 | То же, что | ||
| 3 {4} 3 {3} 3 | 3 | 8 | 3 {} | 1 | 3 {4} 3 | 3 {12} 2 | ||||
| 4 [3] 4 [3] 4 | 4 {3} 4 {3} 4 | 1 | 6 | 4 {} | 1 | 4 {3} 4 | 4 {4} 4 | Самодвойственный, то же, что | ||
| 4 [3] 4 [4] 2 | 4 {3} 4 {4} 2 | 1 | 12 | 4 {} | 3 | 4 {3} 4 | 2 {8} 4 | То же, что | ||
| 2 {4} 4 {3} 4 | 3 | 12 | {} | 1 | 2 {4} 4 | 4 {4} 4 | ||||
Регулярные сложные 3-апейротопы
[ редактировать ]В организме 16 правильных сложных апейротопов. . Коксетер выражает 12 из них через δ п , р
3 , где q ограничено так, чтобы удовлетворять q = 2/(1 – ( p + r )/ pr ) . Их также можно разложить на апейротопы продуктов: ![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Первый случай – это кубические соты .
. Первый случай – это кубические соты .
| Космос | Группа | 3-апейротоп | Вертекс | Край | Лицо | Клетка | привык к нам апейрогон | Примечания |
|---|---|---|---|---|---|---|---|---|
| п [4] 2 [3] 2 [4] р | д п , р 3 = п {4} 2 {3} 2 {4} р | п {} | п {4} 2 | п {4} 2 {3} 2 | п { q } р | То же, что | ||
| 2 [4] 2 [3] 2 [4] 2 =[4,3,4] | д 2,2 3 = 2 {4} 2 {3} 2 {4} 2 | {} | {4} | {4,3} | Кубические соты То же, что | |||
| 3 [4] 2 [3] 2 [4] 2 | д 3,2 3 = 3 {4} 2 {3} 2 {4} 2 | 3 {} | 3 {4} 2 | 3 {4} 2 {3} 2 | То же, что | |||
| д 2,3 3 = 2 {4} 2 {3} 2 {4} 3 | {} | {4} | {4,3} | То же, что | ||||
| 3 [4] 2 [3] 2 [4] 3 | д 3,3 3 = 3 {4} 2 {3} 2 {4} 3 | 3 {} | 3 {4} 2 | 3 {4} 2 {3} 2 | То же, что | |||
| 4 [4] 2 [3] 2 [4] 2 | д 4,2 3 = 4 {4} 2 {3} 2 {4} 2 | 4 {} | 4 {4} 2 | 4 {4} 2 {3} 2 | То же, что | |||
| д 2,4 3 = 2 {4} 2 {3} 2 {4} 4 | {} | {4} | {4,3} | То же, что | ||||
| 4 [4] 2 [3] 2 [4] 4 | д 4,4 3 = 4 {4} 2 {3} 2 {4} 4 | 4 {} | 4 {4} 2 | 4 {4} 2 {3} 2 | То же, что | |||
| 6 [4] 2 [3] 2 [4] 2 | д 6,2 3 = 6 {4} 2 {3} 2 {4} 2 | 6 {} | 6 {4} 2 | 6 {4} 2 {3} 2 | То же, что | |||
| д 2,6 3 = 2 {4} 2 {3} 2 {4} 6 | {} | {4} | {4,3} | То же, что | ||||
| 6 [4] 2 [3] 2 [4] 3 | д 6,3 3 = 6 {4} 2 {3} 2 {4} 3 | 6 {} | 6 {4} 2 | 6 {4} 2 {3} 2 | То же, что | |||
| д 3,6 3 = 3 {4} 2 {3} 2 {4} 6 | 3 {} | 3 {4} 2 | 3 {4} 2 {3} 2 | То же, что | ||||
| 6 [4] 2 [3] 2 [4] 6 | д 6,6 3 = 6 {4} 2 {3} 2 {4} 6 | 6 {} | 6 {4} 2 | 6 {4} 2 {3} 2 | То же, что |
| Космос | Группа | 3-апейротоп | Вертекс | Край | Лицо | Клетка | привык к нам апейрогон | Примечания |
|---|---|---|---|---|---|---|---|---|
| 2 [4] 3 [3] 3 [3] 3 | 3 {3} 3 {3} 3 {4} 2 | 1 | 24 3 {} | 27 3 {3} 3 | 2 3 {3} 3 {3} 3 | 3 {4} 6 | То же, что | |
| 2 {4} 3 {3} 3 {3} 3 | 2 | 27 {} | 24 2 {4} 3 | 1 2 {4} 3 {3} 3 | 2 {12} 3 | |||
| 2 [3] 2 [4] 3 [3] 3 | 2 {3} 2 {4} 3 {3} 3 | 1 | 27 {} | 72 2 {3} 2 | 8 2 {3} 2 {4} 3 | 2 {6} 6 | ||
| 3 {3} 3 {4} 2 {3} 2 | 8 | 72 3 {} | 27 3 {3} 3 | 1 3 {3} 3 {4} 2 | 3 {6} 3 | То же, что |
Регулярные сложные 4-апейротопы
[ редактировать ]В организме 15 правильных сложных апейротопов. . Коксетер выражает 12 из них через δ п , р
4 , где q ограничено так, чтобы удовлетворять q = 2/(1 – ( p + r )/ pr ) . Их также можно разложить на апейротопы продуктов: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Первый случай – это тессерактические соты . Соты с 16 ячейками и соты с 24 ячейками являются реальными решениями. Последнее полученное решение содержит элементы многогранника Виттинга .
. Первый случай – это тессерактические соты . Соты с 16 ячейками и соты с 24 ячейками являются реальными решениями. Последнее полученное решение содержит элементы многогранника Виттинга .
| Космос | Группа | 4-апейротоп | Вертекс | Край | Лицо | Клетка | 4-сторонний | привык к нам апейрогон | Примечания |
|---|---|---|---|---|---|---|---|---|---|
| п [4] 2 [3] 2 [3] 2 [4] р | д п , р 4 = п {4} 2 {3} 2 {3} 2 {4} р | п {} | п {4} 2 | п {4} 2 {3} 2 | п {4} 2 {3} 2 {3} 2 | п { q } р | То же, что | ||
| 2 [4] 2 [3] 2 [3] 2 [4] 2 | д 2,2 4 = {4,3,3,3} | {} | {4} | {4,3} | {4,3,3} | {∞} | Тессерактические соты То же, что | ||
| 2 [3] 2 [4] 2 [3] 2 [3] 2 =[3,4,3,3] | {3,3,4,3} | 1 | 12 {} | 32 {3} | 24 {3,3} | 3 {3,3,4} | Настоящие 16-ячеистые соты То же, что | ||
| {3,4,3,3} | 3 | 24 {} | 32 {3} | 12 {3,4} | 1 {3,4,3} | Настоящие соты из 24 ячеек То же, что | |||
| 3 [3] 3 [3] 3 [3] 3 [3] 3 | 3 {3} 3 {3} 3 {3} 3 {3} 3 | 1 | 80 3 {} | 270 3 {3} 3 | 80 3 {3} 3 {3} 3 | 1 3 {3} 3 {3} 3 {3} 3 | 3 {4} 6 | представительство 5 21 |
Регулярные сложные 5-апейротопы и выше
[ редактировать ]В организме всего 12 правильных сложных апейротопов. или выше, [35] выраженный δ п , р
n где q ограничено так, чтобы удовлетворять q = 2/(1 – ( p + r )/ pr ) . Их также можно разложить на произведение n апейрогонов: ![]()
![]()
![]()
![]()
![]() ...
... ![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]() ...
... ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Первый случай - реальный Гиперкубические соты .
. Первый случай - реальный Гиперкубические соты .
| Космос | Группа | 5-апейротопы | Вершины | Край | Лицо | Клетка | 4-сторонний | 5-гранный | привык к нам апейрогон | Примечания |
|---|---|---|---|---|---|---|---|---|---|---|
| п [4] 2 [3] 2 [3] 2 [3] 2 [4] р | д п , р 5 = п {4} 2 {3} 2 {3} 2 {3} 2 {4} р | п {} | п {4} 2 | п {4} 2 {3} 2 | п {4} 2 {3} 2 {3} 2 | п {4} 2 {3} 2 {3} 2 {3} 2 | п { q } р | То же, что | ||
| 2 [4] 2 [3] 2 [3] 2 [3] 2 [4] 2 =[4,3,3,3,4] | д 2,2 5 = {4,3,3,3,4} | {} | {4} | {4,3} | {4,3,3} | {4,3,3,3} | {∞} | 5-кубовые соты То же, что |
полигон Ван Осса
[ редактировать ]
Многоугольник Ван Осса — это правильный многоугольник на плоскости (вещественная плоскость). , или унитарная плоскость ), в котором лежат ребро и центр тяжести правильного многогранника и образованы из элементов многогранника. Не все правильные многогранники имеют многоугольники Ван Осса.
Например, многоугольники Ван Осса настоящего октаэдра — это три квадрата, плоскости которых проходят через его центр. Напротив, куб не имеет многоугольника Ван Осса, потому что плоскость от края до центра пересекает по диагонали две квадратные грани, а два ребра куба, лежащие в плоскости, не образуют многоугольник.
Бесконечные соты также имеют апейрогоны Ван Осса . Например, вещественная квадратная мозаика и треугольная мозаика имеют апейрогоны {∞} ван Осса. [36]
Если он существует, то многоугольник Ван Осса правильного комплексного многогранника вида p { q } r { s } t ... имеет p -рёбра.
Неправильные комплексные многогранники
[ редактировать ]Произведение сложных многогранников
[ редактировать ]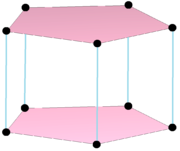 Сложный многоугольник продукта | 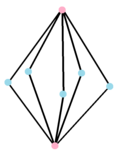 Двойной многоугольник {}+ 5 {} имеет 7 вершин с центрами на краях оригинала, соединенных 10 ребрами. Ее реальное представление — пятиугольная бипирамида . |
Некоторые сложные многогранники можно представить в виде декартовых произведений . Эти многогранники-продукты не являются строго правильными, поскольку они будут иметь более одного типа граней, но некоторые из них могут представлять более низкую симметрию правильных форм, если все ортогональные многогранники идентичны. Например, произведение p {}× p {} или ![]()
![]()
![]() двух одномерных многогранников совпадает с регулярным p {4} 2 или
двух одномерных многогранников совпадает с регулярным p {4} 2 или ![]()
![]()
![]() . Более общие продукты, такие как p {}× q {}, имеют вещественные представления в виде 4-мерных p - q дуопризм . Двойственный многограннику-продукту можно записать в виде суммы p {}+ q {} и иметь действительные представления в виде 4-мерной p - q дуопирамиды . Симметрия p {}+ p {} может быть удвоена как правильный комплексный многогранник 2 {4} p или
. Более общие продукты, такие как p {}× q {}, имеют вещественные представления в виде 4-мерных p - q дуопризм . Двойственный многограннику-продукту можно записать в виде суммы p {}+ q {} и иметь действительные представления в виде 4-мерной p - q дуопирамиды . Симметрия p {}+ p {} может быть удвоена как правильный комплексный многогранник 2 {4} p или ![]()
![]()
![]() .
.
Аналогично, Комплексный многогранник можно построить как тройное произведение: p {}× p {}× p {} или ![]()
![]()
![]()
![]()
![]() то же самое, что и обычный обобщенный куб , p {4} 2 {3} 2 или
то же самое, что и обычный обобщенный куб , p {4} 2 {3} 2 или ![]()
![]()
![]()
![]()
![]() , а также произведение p {4} 2 × p {} или
, а также произведение p {4} 2 × p {} или ![]()
![]()
![]()
![]()
![]() . [37]
. [37]
Квазиправильные многоугольники
[ редактировать ]Квазиправильный усечение многоугольник – это правильного многоугольника. Квазиправильный многоугольник ![]()
![]()
![]() содержит альтернативные ребра правильных многоугольников
содержит альтернативные ребра правильных многоугольников ![]()
![]()
![]() и
и ![]()
![]()
![]() . Квазиправильный многоугольник имеет p вершин на p-ребрах правильной формы.
. Квазиправильный многоугольник имеет p вершин на p-ребрах правильной формы.
Квазиправильные апейрогоны
[ редактировать ]Существует семь квазиправильных комплексных апейрогонов, которые чередуют ребра правильного апейрогона и правильного двойственного ему апейрогона. Расположение вершин этих апейрогонов имеет вещественные представления с правильными и однородными мозаиками евклидовой плоскости. Последний столбец для апейрогона 6{3}6 не только самодвойственный, но и двойственный совпадает сам с собой с перекрывающимися шестиугольными рёбрами, поэтому их квазиправильная форма также имеет перекрывающиеся шестиугольные рёбра, поэтому его нельзя нарисовать двумя чередующимися цветами. как и другие. Симметрию самодуальных семейств можно удвоить, создав таким образом геометрию, идентичную правильной форме: ![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
| п [ q ] р | 4 [8] 2 | 4 [4] 4 | 6 [6] 2 | 6 [4] 3 | 3 [12] 2 | 3 [6] 3 | 6 [3] 6 |
|---|---|---|---|---|---|---|---|
| Обычный |  |  |  |  |  |  | 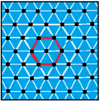 |
| Квазирегулярный |  |  |  |  | 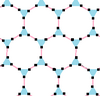 |  |  |
| Обычный двойной |  |  |  |  |  |  | 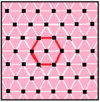 |
Квазиправильные многогранники
[ редактировать ]




 , до исправленного предела, показывая обведенные зелеными треугольниками грани в начале и синие 2 {4} 3 ,
, до исправленного предела, показывая обведенные зелеными треугольниками грани в начале и синие 2 {4} 3 , 

 , фигуры вершин расширяются как новые грани.
, фигуры вершин расширяются как новые грани. Как и реальные многогранники, сложный квазиправильный многогранник можно построить как спрямление (полное усечение ) правильного многогранника. Вершины создаются посередине правильного многогранника, а грани правильного многогранника и его двойника располагаются поочередно по общим ребрам.
Например, p-обобщенный куб, ![]()
![]()
![]()
![]()
![]() , имеет п 3 вершины, 3 п. 2 ребра и 3 p p -обобщенные квадратные грани, а p -обобщенный октаэдр,
, имеет п 3 вершины, 3 п. 2 ребра и 3 p p -обобщенные квадратные грани, а p -обобщенный октаэдр, ![]()
![]()
![]()
![]()
![]() , имеет 3 p вершины, 3 p 2 края и п 3 треугольные лица. Средняя квазиправильная форма p -обобщенный кубооктаэдр,
, имеет 3 p вершины, 3 p 2 края и п 3 треугольные лица. Средняя квазиправильная форма p -обобщенный кубооктаэдр, ![]()
![]()
![]()
![]()
![]() , имеет 3 п 2 вершины, 3 п. 3 края, и 3 п + п 3 лица.
, имеет 3 п 2 вершины, 3 п. 3 края, и 3 п + п 3 лица.
Также выпрямление гессенского многогранника. ![]()
![]()
![]()
![]()
![]() , является
, является ![]()
![]()
![]()
![]()
![]() , квазиправильная форма, имеющая геометрию правильного комплексного многогранника.
, квазиправильная форма, имеющая геометрию правильного комплексного многогранника. ![]()
![]()
![]()
![]()
![]() .
.
| Обобщенный куб/октаэдры | Гессенский многогранник | |||||
|---|---|---|---|---|---|---|
| р=2 (реальный) | р=3 | р=4 | р=5 | р=6 | ||
| Обобщенный кубики (обычный) |  Куб | 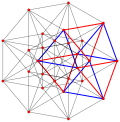 |  | 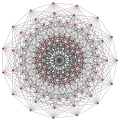 |  |  |
| Обобщенный кубооктаэдры (квазирегулярный) | 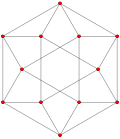 Кубооктаэдр | 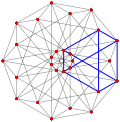 |  | 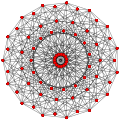 | 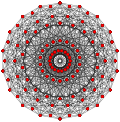 | 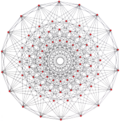 |
| Обобщенный октаэдры (обычный) |  Октаэдр | 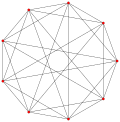 |  | 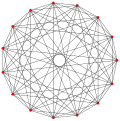 |  |  |
Другие сложные многогранники с унитарными отражениями второго периода.
[ редактировать ]Другие нерегулярные комплексные многогранники могут быть построены внутри унитарных групп отражений, которые не образуют линейных графов Кокстера. На диаграммах Кокстера с петлями Коксетер отмечает интерьер особого периода, например ![]()
![]()
![]() или символ (1 1 1 1) 3 , и группа [1 1 1] 3 . [38] [39] Эти сложные многогранники систематически не исследовались, за исключением нескольких случаев.
или символ (1 1 1 1) 3 , и группа [1 1 1] 3 . [38] [39] Эти сложные многогранники систематически не исследовались, за исключением нескольких случаев.
Группа ![]()
![]()
![]() определяется тремя унитарными отражениями, R 1 , R 2 , R 3 , все порядка 2: R 1 2 = Р1 2 = Р 3 2 = (р 1 р 2 ) 3 = (р 2 р 3 ) 3 = (р 3 р 1 ) 3 = (р 1 р 2 р 3 р 1 ) п = 1. Период p можно рассматривать как двойной оборот в реальном .
определяется тремя унитарными отражениями, R 1 , R 2 , R 3 , все порядка 2: R 1 2 = Р1 2 = Р 3 2 = (р 1 р 2 ) 3 = (р 2 р 3 ) 3 = (р 3 р 1 ) 3 = (р 1 р 2 р 3 р 1 ) п = 1. Период p можно рассматривать как двойной оборот в реальном .
Как и во всех конструкциях Витхоффа , многогранниках, порожденных отражениями, количество вершин однокольцевого многогранника диаграммы Коксетера равно порядку группы, делённому на порядок подгруппы, из которой удален кольцевой узел. Например, реальный куб имеет диаграмму Кокстера. ![]()
![]()
![]()
![]()
![]() , с октаэдрической симметрией
, с октаэдрической симметрией ![]()
![]()
![]()
![]()
![]() порядок 48 и диэдральная симметрия подгруппы
порядок 48 и диэдральная симметрия подгруппы ![]()
![]()
![]() порядка 6, поэтому количество вершин куба равно 48/6=8. Фасеты создаются путем удаления одного узла, самого дальнего от узла с кольцом, например
порядка 6, поэтому количество вершин куба равно 48/6=8. Фасеты создаются путем удаления одного узла, самого дальнего от узла с кольцом, например ![]()
![]()
![]() для куба. Фигуры вершин генерируются путем удаления окольцованного узла и окольцовывания одного или нескольких связанных узлов, и
для куба. Фигуры вершин генерируются путем удаления окольцованного узла и окольцовывания одного или нескольких связанных узлов, и ![]()
![]()
![]() для куба.
для куба.
Коксетер представляет эти группы следующими символами. Некоторые группы имеют одинаковый порядок, но разную структуру, определяющую одно и то же расположение вершин в сложных многогранниках, но разные ребра и более высокие элементы, например ![]()
![]()
![]() и
и ![]()
![]()
![]()
![]() с р ≠3. [40]
с р ≠3. [40]
| Диаграмма Кокстера | Заказ | Символ или позиция в Таблице VII Шепарда и Тодда (1954) |
|---|---|---|
| п п - 1 п !, р ≥ 3 | г ( п , п , п ), [ п ], [1 1 1] п , [1 1 ( п −2) п ] 3 | |
| 72·6!, 108·9! | Нас. 33, 34, [1 2 2] 3 , [1 2 3] 3 | |
| 14·4!, 3·6!, 64·5! | Нас. 24, 27, 29 |
Коксетер называет некоторые из этих сложных многогранников почти правильными, поскольку они имеют правильные грани и фигуры вершин. Первый представляет собой форму более низкой симметрии обобщенного кросс-многогранника в . Второй — дробный обобщенный куб, сводящий p -ребра в отдельные вершины, оставляя обычные 2-ребра. Три из них связаны с конечным правильным косым многогранником в .
| Космос | Группа | Заказ | Коксетер символы | Вершины | Края | Лица | Вертекс фигура | Примечания |
|---|---|---|---|---|---|---|---|---|
| [1 1 1 п ] 3 р =2,3,4... | 6 р. 2 | (1 1 1 1 п ) 3 | 33р | 33р 2 | {3} | {2 п } | Символ пастуха (1 1; 1 1 ) п то же, что β п 3 = | |
| (1 1 1 1 п ) 3 | п 2 | {3} | {6} | Символ пастуха (1 1 1; 1) п 1/ шт . п 3 | ||||
| [1 1 1 2 ] 3 | 24 | (1 1 1 1 2 ) 3 | 6 | 12 | 8 {3} | {4} | То же, что β 2 3 = | |
| (1 1 1 1 2 ) 3 | 4 | 6 | 4 {3} | {3} | 1/2 стакана 2 3 = | |||
| [1 1 1] 3 | 54 | (1 1 1 1 ) 3 | 9 | 27 | {3} | {6} | Символ пастуха (1 1; 1 1 ) 3 то же, что β 3 3 = | |
| (1 1 1 1) 3 | 9 | 27 | {3} | {6} | Символ пастуха (1 1 1; 1) 3 1/3 стакана 3 3 = б 3 3 | |||
| [1 1 1 4 ] 3 | 96 | (1 1 1 1 4 ) 3 | 12 | 48 | {3} | {8} | Символ пастуха (1 1; 1 1 ) 4 то же, что β 4 3 = | |
| (1 1 1 1 4 ) 3 | 16 | {3} | {6} | Символ пастуха (1 1 1; 1) 4 1/4 стакана 4 3 | ||||
| [1 1 1 5 ] 3 | 150 | (1 1 1 1 5 ) 3 | 15 | 75 | {3} | {10} | Символ пастуха (1 1; 1 1 ) 5 то же, что β 5 3 = | |
| (1 1 1 1 5 ) 3 | 25 | {3} | {6} | Символ пастуха (1 1 1; 1) 5 1/5 ц 5 3 | ||||
| [1 1 1 6 ] 3 | 216 | (1 1 1 1 6 ) 3 | 18 | 216 | {3} | {12} | Символ пастуха (1 1; 1 1 ) 6 то же, что β 6 3 = | |
| (1 1 1 1 6 ) 3 | 36 | {3} | {6} | Символ пастуха (1 1 1; 1) 6 1/6 ц 6 3 | ||||
| [1 1 1 4 ] 4 | 336 | (1 1 1 1 4 ) 4 | 42 | 168 | 112 {3} | {8} | представление {3,8|,4} = {3,8} 8 | |
| (1 1 1 1 4 ) 4 | 56 | {3} | {6} | |||||
| [1 1 1 5 ] 4 | 2160 | (1 1 1 1 5 ) 4 | 216 | 1080 | 720 {3} | {10} | представление {3,10|,4} = {3,10} 8 | |
| (1 1 1 1 5 ) 4 | 360 | {3} | {6} | |||||
| [1 1 1 4 ] 5 | (1 1 1 1 4 ) 5 | 270 | 1080 | 720 {3} | {8} | представление {3,8|,5} = {3,8} 10 | ||
| (1 1 1 1 4 ) 5 | 360 | {3} | {6} |
Коксетер определяет другие группы с антиунитарными конструкциями, например эти три. Первый был обнаружен и нарисован Питером Макмалленом в 1966 году. [42]
| Космос | Группа | Заказ | Коксетер символы | Вершины | Края | Лица | Вертекс фигура | Примечания |
|---|---|---|---|---|---|---|---|---|
| [1 1 4 1 4 ] (3) | 336 | (1 1 1 4 1 4 ) (3) | 56 | 168 | 84 {4} | {6} | представление {4,6|,3} = {4,6} 6 | |
| [1 5 1 4 1 4 ] (3) | 2160 | (1 1 5 1 4 1 4 ) (3) | 216 | 1080 | 540 {4} | {10} | представление {4,10|,3} = {4,10} 6 | |
| [1 4 1 5 1 5 ] (3) | (1 1 4 1 5 1 5 ) (3) | 270 | 1080 | 432 {5} | {8} | представление {5,8|,3} = {5,8} 6 |
| Космос | Группа | Заказ | Коксетер символы | Вершины | Другой элементы | Клетки | Вертекс фигура | Примечания |
|---|---|---|---|---|---|---|---|---|
| [1 1 2 п ] 3 р =2,3,4... | 24 р. 3 | (1 1 2 2 п ) 3 | 4 р. | Шепард (2 2 1; 1) п то же, что β п 4 = | ||||
| (1 1 1 2 п ) 3 | п 3 | Шепард (2 1; 1 1 ) п 1/ шт . п 4 | ||||||
| [1 1 2 2 ] 3 =[3 1,1,1 ] | 192 | (1 1 2 2 2 ) 3 | 8 | 24 края 32 лица | 16 | б 2 4 = | ||
| (1 1 1 2 2 ) 3 | 1/2 стакана 2 4 = 4 , настоящий 16-клеточный | |||||||
| [1 1 2] 3 | 648 | (1 1 2 2 ) 3 | 12 | Шепард (2 2 1; 1) 3 то же, что β 3 4 = | ||||
| (1 1 1 2 3 ) 3 | 27 | Шепард (2 1; 1 1 ) 3 1/3 стакана 3 4 | ||||||
| [1 1 2 4 ] 3 | 1536 | (1 1 2 2 4 ) 3 | 16 | Шепард (2 2 1; 1) 4 то же, что β 4 4 = | ||||
| (1 1 1 2 4 ) 3 | 64 | Шепард (2 1; 1 1 ) 4 1/4 стакана 4 4 | ||||||
| [1 4 1 2] 3 | 7680 | (2 2 1 4 1) 3 | 80 | Шепард (2 2 1; 1) 4 | ||||
| (1 1 4 1 2) 3 | 160 | Шепард (2 1; 1 1 ) 4 | ||||||
| (1 1 1 4 2) 3 | 320 | Шепард (2 1 1 ; 1) 4 | ||||||
| [1 1 2] 4 | (1 1 2 2 ) 4 | 80 | 640 ребер 1280 треугольников | 640 | ||||
| (1 1 1 2) 4 | 320 |
| Космос | Группа | Заказ | Коксетер символы | Вершины | Края | Фасеты | Вертекс фигура | Примечания |
|---|---|---|---|---|---|---|---|---|
| [1 1 3 п ] 3 р =2,3,4... | 120 р. 4 | (1 1 3 3 п ) 3 | 5 р. | Шепард (3 3 1; 1) п то же, что β п 5 = | ||||
| (1 1 1 3 п ) 3 | п 4 | Шепард (3 1; 1 1 ) п 1/ шт . п 5 | ||||||
| [2 2 1] 3 | 51840 | (2 1 2 2 ) 3 | 80 | Шепард (2 1; 2 2 ) 3 | ||||
| (2 1 1 2) 3 | 432 | Шепард (2 1 1 ; 2) 3 |
| Космос | Группа | Заказ | Коксетер символы | Вершины | Края | Фасеты | Вертекс фигура | Примечания |
|---|---|---|---|---|---|---|---|---|
| [1 1 4 п ] 3 р =2,3,4... | 720 р. 5 | (1 1 4 4 п ) 3 | 6 р. | Шепард (4 4 1; 1) п то же, что β п 6 = | ||||
| (1 1 1 4 п ) 3 | п 5 | Шепард (4 1; 1 1 ) п 1/ шт . п 6 | ||||||
| [1 2 3] 3 | 39191040 | (2 1 3 3 ) 3 | 756 | Шепард (2 1; 3 3 ) 3 | ||||
| (2 2 1 3) 3 | 4032 | Шепард (2 2 1; 3) 3 | ||||||
| (2 1 1 3) 3 | 54432 | Шепард (2 1 1 ; 3) 3 |
Визуализации
[ редактировать ]- (1 1 1 1 4 ) 4 ,



 имеет 42 вершины, 168 ребер и 112 треугольных граней, видимых в этой 14-угольной проекции.
имеет 42 вершины, 168 ребер и 112 треугольных граней, видимых в этой 14-угольной проекции. - (1 4 1 4 1 1 ) (3) ,


 имеет 56 вершин, 168 ребер и 84 квадратных грани, как видно в этой 14-угольной проекции.
имеет 56 вершин, 168 ребер и 84 квадратных грани, как видно в этой 14-угольной проекции. - (1 1 2 2 ) 4 ,




 имеет 80 вершин, 640 ребер, 1280 треугольных граней и 640 тетраэдрических ячеек, видимых в этой 20-угольной проекции. [43]
имеет 80 вершин, 640 ребер, 1280 треугольных граней и 640 тетраэдрических ячеек, видимых в этой 20-угольной проекции. [43]
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ Питер Орлик , Виктор Райнер, Энн В. Шеплер. Знаковое представление групп Шепарда . Математические Аннален . Март 2002 г., том 322, выпуск 3, стр. 477–492. DOI:10.1007/s002080200001 [1]
- ^ Коксетер, Правильные комплексные многогранники, с. 115
- ^ Коксетер, Правильные комплексные многогранники , 11.3 Многоугольник Петри , простой h -угольник, образованный орбитой флага (O 0 , O 0 O 1 ) для произведения двух порождающих отражений любого незвездного правильного комплексного многоугольника, p 1 { q } п 2 .
- ^ Комплексные правильные многогранники, 11.1 Правильные комплексные многоугольники стр.103
- ^ Шепард, 1952; «Именно из подобных соображений мы выводим понятие внутренней части многогранника, и будет видно, что в унитарном пространстве, где числа не могут быть упорядочены таким образом, такое понятие внутренней части невозможно. [Парабрейк] Следовательно. ... мы должны рассматривать унитарные многогранники как конфигурации».
- ^ Коксетер, Правильные комплексные многогранники, с. 96
- ^ Коксетер, Правильные комплексные многогранники, с. xiv
- ^ Коксетер, Комплексные правильные многогранники, с. 177, таблица III
- ^ Лерер и Тейлор 2009, с. 87
- ^ Коксетер, Правильные комплексные многогранники, Таблица IV. Правильные многоугольники. стр. 178–179.
- ^ Комплексные многогранники, 8.9 Двумерный случай , с. 88
- ^ Правильные комплексные многогранники, Коксетер, стр. 177-179.
- ^ Перейти обратно: а б Коксетер, Правильные комплексные многогранники, с. 108
- ^ Коксетер, Правильные комплексные многогранники, с. 109
- ^ Коксетер, Правильные комплексные многогранники, с. 111
- ^ Коксетер, Правильные комплексные многогранники, с. 30 схема и стр. 47 индексов для 8 трехгранников
- ^ Перейти обратно: а б Коксетер, Правильные комплексные многогранники, с. 110
- ^ Коксетер, Правильные комплексные многогранники, с. 48
- ^ Коксетер, Правильные комплексные многогранники, с. 49
- ^ Коксетер, Правильные комплексные многогранники, стр. 116–140.
- ^ Перейти обратно: а б Коксетер, Правильные комплексные многогранники, стр. 118–119.
- ^ Комплексные правильные многогранники, стр.29
- ^ Перейти обратно: а б Коксетер, Правильные комплексные многогранники, Таблица V. Незвездные правильные многогранники и 4-многогранники. п. 180.
- ^ Коксетер, Калейдоскопы - Избранные сочинения HSM Коксетера , Статья 25 Удивительные отношения между унитарными группами отражения , стр. 431.
- ^ Перейти обратно: а б Коксетер, Правильные комплексные многогранники, с. 131
- ^ Коксетер, Правильные комплексные многогранники, с. 126
- ^ Коксетер, Правильные комплексные многогранники, с. 125
- ^ Коксетер, Правильные комплексные многогранники, Таблица VI. Обычные соты. п. 180.
- ^ Комплексный правильный многогранник, стр.174
- ^ Коксетер, Правильные комплексные многогранники, Таблица VI. Обычные соты. п. 111, 136.
- ^ Коксетер, Правильные комплексные многогранники, Таблица IV. Правильные многоугольники. стр. 178–179.
- ^ Коксетер, Правильные комплексные многогранники, 11.6 апейрогонов, стр. 111-112.
- ^ Коксетер, Комплексные правильные многогранники, стр.140
- ^ Коксетер, Правильные комплексные многогранники, стр. 139-140.
- ^ Комплексные правильные многогранники, стр.146
- ^ Комплексные правильные многогранники, стр.141
- ^ Коксетер, Правильные комплексные многогранники, стр. 118–119, 138.
- ^ Коксетер, Правильные комплексные многогранники, Глава 14, Почти правильные многогранники , стр. 156–174.
- ^ Коксетер, Группы, порожденные унитарными отражениями второго периода , 1956 г.
- ^ Коксетер , Конечные группы, порожденные унитарными отражениями , 1966, 4. Графические обозначения , Таблица n -мерных групп, порожденных n унитарными отражениями. стр. 422-423
- ^ Перейти обратно: а б с д и Коксетер, Группы, порожденные унитарными отражениями второго периода (1956), Таблица III: Некоторые сложные многогранники, стр. 413
- ^ Коксетер, Комплексные правильные многогранники, (1991), 14.6 Два многогранника Макмаллена с 84 квадратными гранями, стр.166-171
- ^ Коксетер, Комплексные правильные многогранники, стр. 172-173.
Ссылки
[ редактировать ]- Коксетер, HSM и Мозер, WOJ; Генераторы и отношения для дискретных групп (1965), особенно стр. 67–80.
- Коксетер, HSM (1991), Правильные комплексные многогранники , издательство Кембриджского университета, ISBN 0-521-39490-2
- Коксетер, HSM и Шепард, GC; Портреты семейства сложных многогранников, Леонардо Том 25, № 3/4 (1992), стр. 239–244,
- Шепард, GC; Правильные комплексные многогранники , Учеб. Лондонская математика. Соц. Серия 3, Том 2 (1952), стр. 82–97.
- Г.К. Шепард , Дж.А. Тодд, Конечные унитарные группы отражений , Канадский математический журнал. 6(1954), 274-304, два : 10.4153/CJM-1954-028-3
- Густав И. Лерер и Дональд Э. Тейлор, Группы унитарного отражения , Cambridge University Press, 2009 г.
Дальнейшее чтение
[ редактировать ]- Ф. Артур Шерк, Питер МакМаллен, Энтони К. Томпсон и Азия Ивич Вайс, редакторы: Калейдоскопы - Избранные сочинения HSM Coxeter. , Статья 25, Конечные группы, порожденные унитарными отражениями , стр. 415-425, Джон Уайли, 1995, ISBN 0-471-01003-0
- МакМаллен, Питер ; Шульте, Эгон (декабрь 2002 г.), Абстрактные правильные многогранники (1-е изд.), Cambridge University Press , ISBN 0-521-81496-0 Глава 9. Унитарные группы и эрмитовы формы , стр. 289–298.







![{\displaystyle \left[{\begin{smallmatrix}e^{2\pi i/p}&0\\(e^{2\pi i/p}-1)k&1\\\end{smallmatrix}} \right ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d128407ddca614c4bed7308acba9bd274b704c5c)
![{\displaystyle \left[{\begin{smallmatrix}1&(e^{2\pi i/r}-1)k\\0&e^{2\pi i/r}\\\end{smallmatrix}}\right ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de7bd24e7be60162da1fa1566fea5571820d3e82)

![{\displaystyle \left[{\begin{smallmatrix}e^{2\pi i/p}&0\\0&1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/922057855ba2380fdbf36b0e91f0afe08b867bcb)
![{\displaystyle \left[{\begin{smallmatrix}1&0\\0&e^{2\pi i/q}\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6991a4012a94e23b3475fd268007ca2aeba4bcbe)
![{\displaystyle \left[{\begin{smallmatrix}0&1\\1&0\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9694a3311550c844e792232f8c8742c6f3c9d32f)
![{\displaystyle \left[{\begin{smallmatrix}{\frac {-1+{\sqrt {3}}i}{2}}&0\\{\frac {-3+{\sqrt {3}}i }{2}}&1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aef7975113174eb40a8488733bebb8fb4d1bd293)
![{\displaystyle \left[{\begin{smallmatrix}1&{\frac {-3+{\sqrt {3}}i}{2}}\\0&{\frac {-1+{\sqrt {3}} i}{2}}\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1081ee946ee626dd6ae6d776581d567006cd16fb)
![{\displaystyle \left[{\begin{smallmatrix}i&0\\0&1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4087d1ec8773364a46947bc9f58bf721a413846c)
![{\displaystyle \left[{\begin{smallmatrix}1&0\\0&i\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3736413b59866ae2edd640f7bb77f7b8bdd6a9d)
![{\displaystyle \left[{\begin{smallmatrix}1&-2\\0&-1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de49a4aea18b37177252a0f6c2a3707c14b9b910)


![2{4}3, , с 6 вершинами и 9 ребрами[13]](http://upload.wikimedia.org/wikipedia/commons/thumb/7/70/Complex_polygon_2-4-3-bipartite_graph.png/120px-Complex_polygon_2-4-3-bipartite_graph.png)








![3{4}2 или , с 9 вершинами и 6 (треугольными) 3-ребрами[13]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/dc/3-generalized-2-cube_skew.svg/120px-3-generalized-2-cube_skew.svg.png)









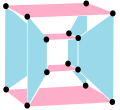

![3{6}2 или , с 24 вершинами черного цвета и 16 3-ребрами, окрашенными в 2 набора 3-ребер красного и синего цвета[14]](http://upload.wikimedia.org/wikipedia/commons/thumb/3/36/Complex_polygon_3-6-2.png/120px-Complex_polygon_3-6-2.png)
![3{8}2 или , с 72 вершинами черного цвета и 48 3-ребрами, окрашенными в 2 набора 3-ребер красным и синим[15]](http://upload.wikimedia.org/wikipedia/commons/thumb/0/00/Complex_polygon_3-8-2.png/120px-Complex_polygon_3-8-2.png)
![3{3}3, или , с 8 вершинами черного цвета и 8 3-ребрами, окрашенными в 2 набора 3-ребер красного и синего цвета[16]](http://upload.wikimedia.org/wikipedia/commons/thumb/e/ef/Complex_polygon_3-3-3.png/120px-Complex_polygon_3-3-3.png)
![3{4}3 или , с 24 вершинами и 24 3-ребрами, показанными в 3 наборах цветов, один набор заполнен[17]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/de/Complex_polygon_3-4-3-fill1.png/120px-Complex_polygon_3-4-3-fill1.png)
![4{3}4 или , с 24 вершинами и 24 4-ребрами, показанными в 4 наборах цветов[17]](http://upload.wikimedia.org/wikipedia/commons/thumb/4/46/Complex_polygon_4-3-4.png/119px-Complex_polygon_4-3-4.png)
![3{5}3 или , со 120 вершинами и 120 3-ребрами[18]](http://upload.wikimedia.org/wikipedia/commons/thumb/2/20/Complex_polygon_3-5-3.png/120px-Complex_polygon_3-5-3.png)
![5{3}5 или , со 120 вершинами и 120 5-ребрами[19]](http://upload.wikimedia.org/wikipedia/commons/thumb/b/b9/Complex_polygon_5-3-5.png/119px-Complex_polygon_5-3-5.png)




![3{3}3{3}3, или , имеет 27 вершин, 72 3-ребра и 27 граней, причем одна грань выделена синим цветом.[25]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/df/Complex_polyhedron_3-3-3-3-3-one-blue-face.png/120px-Complex_polyhedron_3-3-3-3-3-one-blue-face.png)
![2{4}3{3}3, имеет 54 вершины, 216 простых ребер и 72 грани, одна из которых выделена синим цветом.[26]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1d/Complex_polyhedron_2-4-3-3-3_blue-edge.png/120px-Complex_polyhedron_2-4-3-3-3_blue-edge.png)
![3{3}3{4}2, или , имеет 72 вершины, 216 3-ребер и 54 вершины, причем одна грань выделена синим цветом.[27]](http://upload.wikimedia.org/wikipedia/commons/thumb/8/86/Complex_polyhedron_3-3-3-4-2-one-blue-face.png/118px-Complex_polyhedron_3-3-3-4-2-one-blue-face.png)







![3{4}2{3}2, или имеет 27 вершин, 27 3-ребер и 9 граней[25]](http://upload.wikimedia.org/wikipedia/commons/thumb/8/8d/3-generalized-3-cube.svg/118px-3-generalized-3-cube.svg.png)