Сложный самолет
| Математический анализ → Комплексный анализ |
| Комплексный анализ |
|---|
 |
| Комплексные числа |
| Сложные функции |
| Основная теория |
| Геометрическая теория функций |
| Люди |
В математике комплексная плоскость — это плоскость , образованная комплексными числами , с декартовой системой координат , в которой горизонтальная ось X , называемая действительной осью , образована действительными числами , а вертикальная ось Y , называемая мнимой. ось , образована мнимыми числами .
Комплексная плоскость позволяет геометрическую интерпретацию комплексных чисел. При сложении они складывают подобные векторы . Умножение угол двух комплексных чисел проще выразить в полярных координатах : величина или модуль произведения представляет собой произведение двух абсолютных значений или модулей, а или аргумент произведения представляет собой сумму двух углов. или аргументы. В частности, умножение на комплексное число по модулю 1 действует как вращение.
Комплексную плоскость иногда называют плоскостью Аргана или плоскостью Гаусса .
Условные обозначения [ править ]
Комплексные числа [ править ]
В комплексном анализе комплексные числа обычно обозначаются символом z , который можно разделить на действительную ( x ) и мнимую ( y ) части:
например: z = 4 + 5 i , где x и y — действительные числа, а i — мнимая единица . В этих обычных обозначениях комплексное число z соответствует точке ( x , y ) на декартовой плоскости ; точка ( x , y ) также может быть представлена в полярных координатах с помощью:
В декартовой плоскости можно предположить, что диапазон функции арктангенса принимает значения (−π/2, π/2) (в радианах ), и необходимо позаботиться о том, чтобы определить более полную функцию арктангенса для точек ( x , y ), когда x ≤ 0 . [примечание 1] В комплексной плоскости эти полярные координаты принимают вид
где [примечание 2]
Здесь | г | — абсолютное значение или модуль комплексного числа z ; θ , аргумент z θ обычно берется в интервале 0 ≤ ; < 2 π , и последнее равенство (to | z | e я ) берется из формулы Эйлера . Без ограничения на диапазон θ аргумент z является многозначным, поскольку комплексная показательная функция является периодической с периодом 2 πi . Таким образом, если θ — одно значение arg( z ) , остальные значения задаются формулой arg( z ) = θ + 2 nπ , где n — любое ненулевое целое число. [2]
Хотя геометрическое представление комплексных чисел редко используется явно, оно неявно основано на его структуре евклидова векторного пространства размерности 2, где внутренний продукт комплексных чисел w и z определяется выражением ; тогда для комплексного числа z его абсолютное значение | г | совпадает с его евклидовой нормой, а его аргумент arg( z ) с углом поворота от 1 до z .
Теория контурного интегрирования составляет большую часть комплексного анализа. В этом контексте важно направление движения по замкнутой кривой: изменение направления движения кривой на противоположное умножает значение интеграла на −1 . По соглашению положительное направление — против часовой стрелки. Например, единичная окружность проходится в положительном направлении, когда мы начинаем с точки z = 1 , затем перемещаемся вверх и влево через точку z = i , затем вниз и влево через −1 , затем вниз и до направо через − i и, наконец, вверх и вправо до z = 1 , откуда мы начали.
Почти весь комплексный анализ связан со сложными функциями , то есть с функциями, которые отображают некоторое подмножество комплексной плоскости в какое-то другое (возможно, перекрывающееся или даже идентичное) подмножество комплексной плоскости. Здесь принято говорить о области определения f ( z ) как о лежащей в z -плоскости, а область значений ( f z ) — как о наборе точек в w -плоскости. Символами мы пишем
и часто думайте о функции f как о преобразовании из z -плоскости (с координатами ( x , y ) ) в w -плоскость (с координатами ( u , v ) ).
Обозначение сложной плоскости [ править ]
Комплексная плоскость обозначается как .
Аргана [ править] Диаграмма
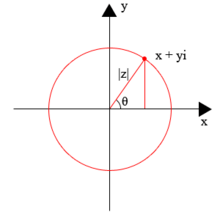
Диаграмма Аргана представляет собой геометрический график комплексных чисел в виде точек z = x + iy с использованием горизонтальной оси x в качестве действительной оси и вертикальной оси y в качестве мнимой оси. [3] Такие участки названы в честь Жана-Робера Аргана (1768–1822), хотя впервые они были описаны норвежско-датским землемером и математиком Каспаром Весселем (1745–1818). [примечание 3] Диаграммы Аргана часто используются для построения положений нулей и полюсов функции на комплексной плоскости.
Стереографические проекции [ править ]

Может оказаться полезным представить комплексную плоскость так, как если бы она занимала поверхность сферы. Дана сфера единичного радиуса, поместим ее центр в начало комплексной плоскости, ориентированный так, чтобы экватор на сфере совпадал с единичным кругом в плоскости, а северный полюс находился «над» плоскостью.
Мы можем установить взаимно однозначное соответствие между точками на поверхности сферы за вычетом северного полюса и точками на комплексной плоскости следующим образом. Дана точка на плоскости и нарисуйте прямую линию, соединяющую ее с северным полюсом сферы. Эта линия пересечет поверхность сферы ровно в одной точке. Точка z = 0 будет спроецирована на южный полюс сферы. Поскольку внутренняя часть единичного круга находится внутри сферы, вся эта область ( | z | < 1 ) будет отображена на южном полушарии. Сам единичный круг ( | z | = 1 ) будет отображен на экваторе, а внешняя часть единичного круга ( | z | > 1 ) будет отображена на северном полушарии за вычетом северного полюса. Очевидно, что эта процедура обратима: если взять любую точку на поверхности сферы, не являющуюся северным полюсом, мы можем провести прямую линию, соединяющую эту точку с северным полюсом и пересекающую плоскую плоскость ровно в одной точке.
В этой стереографической проекции сам северный полюс не связан ни с одной точкой комплексной плоскости. Мы совершенствуем взаимно-однозначное соответствие, добавляя к комплексной плоскости еще одну точку – так называемую точку на бесконечности – и отождествляя ее с северным полюсом сферы. Это топологическое пространство, комплексная плоскость плюс бесконечная точка, известно как расширенная комплексная плоскость . Когда мы обсуждаем комплексный анализ, мы говорим об одной «точке бесконечности». есть две точки на бесконечности (положительная и отрицательная) На прямой действительной числовой линии , но на расширенной комплексной плоскости есть только одна точка на бесконечности (северный полюс). [5]
Представьте себе на минутку, что произойдет с линиями широты и долготы, если их спроецировать со сферы на плоскую плоскость. Все линии широты параллельны экватору, поэтому они станут идеальными кругами с центром в начале координат z = 0 . А линии долготы станут прямыми, проходящим через начало координат (а также через «точку в бесконечности», поскольку они проходят как через северный, так и через южный полюс сферы).
Это не единственная возможная, но правдоподобная стереографическая ситуация проекции сферы на плоскость, состоящую из двух и более величин. Например, северный полюс сферы можно поместить поверх начала координат z = −1 в плоскости, касательной к окружности. Детали не имеют особого значения. Любая стереографическая проекция сферы на плоскость создаст одну «точку в бесконечности» и отобразит линии широты и долготы на сфере в круги и прямые линии соответственно на плоскости.
Разрезание плоскости [ править ]
При обсуждении функций комплексной переменной часто удобно думать о разрезе на комплексной плоскости. Эта идея естественным образом возникает в нескольких различных контекстах.
Многозначные отношения и точки ветвления [ править ]
Рассмотрим простое двузначное отношение
Прежде чем мы сможем рассматривать эту связь как однозначную функцию , необходимо каким-то образом ограничить диапазон результирующего значения. Когда мы имеем дело с квадратными корнями из неотрицательных действительных чисел, это легко сделать. Например, мы можем просто определить
быть неотрицательным действительным числом y таким, что y 2 = х . Эта идея не так хорошо работает в двумерной комплексной плоскости. Чтобы понять почему, давайте подумаем о том, как значение f ( z ) меняется при движении точки z по единичному кругу. Мы можем написать и возьми
Очевидно, что когда z движется по всему кругу, w очерчивает только половину круга. Итак, одно непрерывное движение в комплексной плоскости превратило положительный квадратный корень e 0 = 1 в отрицательный квадратный корень e яπ = −1 .
Эта проблема возникает потому, что точка z = 0 имеет только один квадратный корень, в то время как любое другое комплексное число z ≠ 0 имеет ровно два квадратных корня. На прямой числовой линии мы могли бы обойти эту проблему, воздвигнув «барьер» в единственной точке x = 0 . В комплексной плоскости необходим барьер большего размера, чтобы любой замкнутый контур не мог полностью окружить точку ветвления z = 0 . Обычно это делается путем обрезки ветвей ; в этом случае «разрез» может простираться от точки z = 0 вдоль положительной вещественной оси до точки, находящейся на бесконечности, так что аргумент переменной z в плоскости разреза ограничивается диапазоном 0 ≤ arg( z ) < 2 π .
Теперь мы можем дать полное описание w = z 1/2 . Для этого нам нужны две копии плоскости z , каждая из которых разрезана по действительной оси. На одной копии мы определяем квадратный корень из 1 как e 0 = 1 , а с другой стороны, мы определяем квадратный корень из 1 как e яπ = −1 . Мы называем эти две копии полных разрезанных плоских листов . Приведя аргумент непрерывности, мы видим, что (теперь однозначная) функция w = z 1/2 отображает первый лист в верхнюю половину w -плоскости, где 0 ≤ arg( w ) < π , при этом второй лист отображается в нижнюю половину w -плоскости (где π ≤ arg( w ) < 2 π ) . [6]
Разрез ветки в этом примере не обязательно должен лежать вдоль действительной оси; это даже не обязательно должна быть прямая линия. любая непрерывная кривая, соединяющая начало координат z = 0 Подойдет с точкой на бесконечности. В некоторых случаях срез ветки даже не обязательно должен проходить через точку, находящуюся на бесконечности. Например, рассмотрим отношения
Здесь полином z 2 − 1 исчезает, когда z = ±1 , поэтому очевидно, что g имеет две точки ветвления. Мы можем «разрезать» плоскость по действительной оси, от −1 до 1 , и получить лист, на котором g ( z ) является однозначной функцией. В качестве альтернативы разрез может проходить от z = 1 вдоль положительной вещественной оси через точку на бесконечности, а затем продолжить «вверх» по отрицательной вещественной оси до другой точки ветвления, z = −1 .
Эту ситуацию легче всего визуализировать с помощью описанной выше стереографической проекции . На сфере один из этих разрезов проходит через южное полушарие в продольном направлении, соединяя точку на экваторе ( z = −1 ) с другой точкой на экваторе ( z = 1 ) и проходя через южный полюс (начало координат z = 0 ) в пути. Второй вариант разреза проходит в продольном направлении через северное полушарие и соединяет те же две экваториальные точки, проходя через северный полюс (то есть точку, находящуюся на бесконечности).
Ограничение области применения мероморфных функций [ править ]
Мероморфная функция — это комплексная функция, которая голоморфна и, следовательно, аналитична всюду в своей области определения, за исключением конечного или счетного числа точек. [примечание 4] Точки, в которых такая функция не может быть определена, называются полюсами мероморфной функции. Иногда все эти полюса лежат на одной прямой. В этом случае математики могут сказать, что функция «голоморфна на плоскости сечения». На примере:
, Гамма-функция определяемая формулой
где γ - постоянная Эйлера-Машерони и имеет простые полюса в точках 0, −1, −2, −3, ... потому что ровно один знаменатель в бесконечном произведении обращается в нуль, когда z = 0 или отрицательное целое число. [примечание 5] Поскольку все ее полюса лежат на отрицательной вещественной оси, от z = 0 до точки, находящейся на бесконечности, эту функцию можно описать как «голоморфную на плоскости сечения, при этом разрез простирается вдоль отрицательной вещественной оси от 0 (включительно) до точка в бесконечности».
В качестве альтернативы, Γ( z ) можно было бы описать как «голоморфную в плоскости сечения с − π < arg( z ) < π и исключающую точку z = 0 ».
Этот разрез немного отличается от разреза ветвления, с которым мы уже столкнулись, поскольку он фактически исключает отрицательную действительную ось из плоскости разреза. Разрез ветки оставил действительную ось, соединенную с плоскостью сечения с одной стороны (0 ≤ θ ) , но отделил ее от плоскости сечения с другой стороны ( θ < 2π ) .
Конечно, на самом деле нет необходимости исключать весь отрезок от z = 0 до −∞, чтобы построить область, в которой Γ( z ) голоморфна. Все, что нам действительно нужно сделать, это проколоть плоскость в счетном множестве точек {0, −1, −2, −3, ...} . Но замкнутый контур в проколотой плоскости может окружать один или несколько полюсов Γ( z ) , давая контурный интеграл , который не обязательно равен нулю, согласно теореме о вычетах . Разрезание комплексной плоскости гарантирует не только то, что Γ( z ) голоморфно в этой ограниченной области, но и то, что контурный интеграл гамма-функции по любой замкнутой кривой, лежащей в плоскости разреза, тождественно равен нулю.
Указание регионов сходимости [ править ]
Многие сложные функции определяются бесконечными рядами или цепными дробями . Фундаментальным соображением при анализе этих бесконечно длинных выражений является определение части комплексной плоскости, в которой они сходятся к конечному значению. Разрез в плоскости может облегчить этот процесс, как показывают следующие примеры.
Рассмотрим функцию, определяемую бесконечным рядом
Потому что з 2 знак равно (- z ) 2 для каждого комплексного числа z ясно, что f ( z ) является четной функцией от z , поэтому анализ можно ограничить одной половиной комплексной плоскости. И поскольку ряд не определен, когда
имеет смысл разрезать плоскость по всей мнимой оси и установить сходимость этого ряда, где действительная часть z не равна нулю, прежде чем приступить к более трудной задаче исследования f ( z ), когда z — чисто мнимое число. [примечание 6]
В этом примере разрез является просто удобством, поскольку точки, в которых бесконечная сумма не определена, изолированы, и плоскость разреза можно заменить плоскостью, проколотой подходящим образом . В некоторых случаях сокращение необходимо, а не просто удобно. Рассмотрим бесконечную периодическую цепную дробь
Можно показать , что f ( z ) сходится к конечному значению, если z не является отрицательным действительным числом таким, что z < - 1 ⁄ 4 . Другими словами, областью сходимости этой цепной дроби является плоскость разреза, где разрез проходит вдоль отрицательной вещественной оси, от — 1 ⁄ 4 до бесконечности. [8]
Склеиваем разрезанную плоскость обратно [ править ]
Мы уже видели, как связаны отношения
можно превратить в однозначную функцию, разбив область определения f на два несвязных листа. Также возможно «склеить» эти два листа обратно вместе, чтобы сформировать единую риманову поверхность , на которой f ( z ) = z 1/2 можно определить как голоморфную функцию, образом которой является вся w -плоскость (кроме точки w = 0 ). Вот как это работает.
Представьте себе две копии разрезаемой комплексной плоскости, разрезы простираются вдоль положительной действительной оси от z = 0 до точки на бесконечности. На одном листе определим 0 ≤ arg( z ) < 2 π , так что 1 1/2 = и 0 = 1 по определению. На втором листе определим 2 π ≤ arg( z ) < 4 π , так что 1 1/2 = и яπ = −1 , опять же по определению. Теперь переверните второй лист вверх дном так, чтобы воображаемая ось указывала в направлении, противоположном воображаемой оси первого листа, причем обе реальные оси были направлены в одном направлении, и «склейте» два листа вместе (так, чтобы край на первый лист с меткой « θ = 0 » соединен с ребром с меткой « θ < 4 π » на втором листе, а ребро на втором листе с меткой « θ = 2 π » соединено с ребром с меткой « θ < 2». π » на первом листе). В результате получается область римановой поверхности, на которой f ( z ) = z 1/2 является однозначным и голоморфным (за исключением случаев, когда z = 0 ). [6]
Чтобы понять, почему f является однозначным в этой области, представьте себе контур вокруг единичной окружности, начиная с z = 1 на первом листе. Когда 0 ≤ θ < 2 π, мы все еще находимся на первом листе. Когда θ = 2 π, мы перешли на второй лист и должны сделать второй полный обход вокруг точки ветвления z = 0, прежде чем вернуться в нашу исходную точку, где θ = 4 π эквивалентно θ = 0 , потому что о том, как мы склеили два листа вместе. Другими словами, поскольку переменная z делает два полных оборота вокруг точки ветвления, образ z в w -плоскости очерчивает только одну полную окружность.
Формальное дифференцирование показывает, что
откуда мы можем заключить, что производная f существует и конечна всюду на римановой поверхности, кроме случаев, когда z = 0 (т. е. f голоморфна, за исключением случаев, когда z = 0 ).
Как можно определить риманову поверхность для функции
также обсуждалось выше , быть построенным? Мы снова начинаем с двух копий z -плоскости, но на этот раз каждая из них разрезается по реальному отрезку, простирающемуся от z = −1 до z = 1 – это две точки ветвления g ( z ) . Мы переворачиваем один из них вверх дном так, чтобы две воображаемые оси были направлены в противоположные стороны, и склеиваем соответствующие края двух разрезанных листов вместе. Мы можем убедиться, что g является однозначной функцией на этой поверхности, проведя контур вокруг круга единичного радиуса с центром в точке z = 1 . Начиная с точки z = 2 на первом листе, мы поворачиваем половину круга, прежде чем встретить разрез в точке z = 0 . Разрез вынуждает нас перейти на второй лист, так что, когда z сделал один полный оборот вокруг точки ветвления z = 1 , w сделал только половину полного оборота, знак w поменялся на противоположный (потому что e яπ = −1 ), и наш путь привел нас к точке z = 2 на втором листе поверхности. Продолжая еще пол-оборота, мы встречаем другую сторону разреза, где z = 0 , и, наконец, достигаем нашей начальной точки ( z = 2 на первом листе), сделав два полных оборота вокруг точки ветвления.
Естественный способ обозначить θ = arg( z ) в этом примере — установить − π < θ ≤ π на первом листе, при этом π < θ ≤ 3 π на втором. Воображаемые оси на двух листах направлены в противоположные стороны, так что сохраняется направление положительного вращения против часовой стрелки при перемещении замкнутого контура с одного листа на другой (помните, второй лист перевернут ) . Представьте себе эту поверхность, встроенную в трехмерное пространство, причем оба листа параллельны плоскости xy . Затем на поверхности появляется вертикальное отверстие, где два разреза соединяются вместе. Что, если разрез будет сделан от z = −1 вниз по действительной оси до точки, находящейся на бесконечности, и от z = 1 вверх по действительной оси, пока разрез не встретится сам с собой? Снова можно построить риманову поверхность, но на этот раз «дырка» горизонтальна. С топологической точки зрения обе версии этой римановой поверхности эквивалентны — они представляют собой ориентируемые двумерные поверхности рода один.
в управления Использование теории
В теории управления одно из применений комплексной плоскости известно как s-плоскость . Он используется для графической визуализации корней уравнения, описывающего поведение системы (характеристическое уравнение). Уравнение обычно выражается в виде многочлена от параметра s , преобразования Лапласа отсюда и название s -плоскость. Точки в s-плоскости принимают форму s = σ + jω , где ' j ' используется вместо обычного ' i ' для обозначения мнимой составляющей (переменная ' i ' часто используется для обозначения электрического тока в инженерных контекстах) .
Другое связанное использование комплексной плоскости связано с критерием устойчивости Найквиста . Это геометрический принцип, который позволяет определять стабильность системы с обратной связью с обратной связью путем проверки графика Найквиста ее величины и фазовой характеристики в разомкнутом контуре как функции частоты (или передаточной функции контура ) в комплексной плоскости.
Z - плоскость представляет собой -плоскости с дискретным временем версию s , где z -преобразования вместо преобразования Лапласа используются .
Квадратичные пространства [ править ]
Комплексная плоскость связана с двумя различными квадратичными пространствами . Для точки z = x + iy на комплексной плоскости квадратичная функция z 2 и квадрат нормы x 2 + и 2 обе квадратичные формы . Первым часто пренебрегают после использования второго для задания метрики на комплексной плоскости. Эти отдельные грани комплексной плоскости как квадратичного пространства возникают при построении алгебр над полем с процессом Кэли-Диксона . Эту процедуру можно применить к любому полю , и для полей R и C получаются разные результаты : когда R является взлетным полем, тогда C строится с квадратичной формой x 2 + и 2 , но процесс также может начинаться с C и z 2 , и этот случай порождает алгебры, отличные от алгебр, полученных из R . В любом случае генерируемые алгебры являются композиционными алгебрами ; в этом случае комплексная плоскость является множеством точек для двух различных композиционных алгебр.
Другие значения слова «сложная плоскость» [ править ]
Предыдущие разделы этой статьи посвящены комплексной плоскости с точки зрения геометрического представления комплексных чисел. Хотя использование термина «комплексная плоскость» имеет долгую и богатую с математической точки зрения историю, это ни в коем случае не единственное математическое понятие, которое можно охарактеризовать как «комплексная плоскость». Есть как минимум три дополнительных возможности.
- Двумерное комплексное векторное пространство, «комплексная плоскость» в том смысле, что это двумерное векторное пространство, координаты которого являются комплексными числами . См. также: Комплексное аффинное пространство § Два измерения .
- (1 + 1) -мерное пространство Минковского , также известное как расщепленно-комплексная плоскость , представляет собой «комплексную плоскость» в том смысле, что алгебраические расщепленно-комплексные числа можно разделить на две вещественные компоненты, которые легко сопоставляются с точкой ( x , y ) в декартовой плоскости.
- Набор двойственных чисел над действительными числами также может быть помещен во взаимно однозначное соответствие точкам ( x , y ) декартовой плоскости и представлять собой еще один пример «комплексной плоскости».
См. также [ править ]
- Комплексное координатное пространство
- Сложная геометрия
- Сложная линия
- Диаграмма созвездия
- Сфера Римана , представляющая собой расширенную комплексную плоскость.
- S-плоскость
- Синфазные и квадратурные составляющие
- Реальная линия
Примечания [ править ]
- ^ Подробное определение комплексного аргумента в терминах полного арктангенса можно найти в описании функции atan2 .
- ^ Все знакомые свойства комплексной показательной функции, тригонометрических функций и комплексного логарифма можно вывести непосредственно из степенного ряда для e С . В частности, главное значение log r , где | р | = 1 , можно вычислить без обращения к какой-либо геометрической или тригонометрической конструкции. [1]
- ^ Мемуары Весселя были представлены Датской академии в 1797 году; Статья Аргана была опубликована в 1806 году. [4]
- ^ См. также Доказательство того, что голоморфные функции аналитичны .
- ^ Бесконечное произведение для Γ( z ) в равномерно сходится любой ограниченной области, где ни один из его знаменателей не обращается в нуль; следовательно, он определяет мероморфную функцию на комплексной плоскости. [7]
- ^ При Re( z ) > 0 эта сумма сходится равномерно в любой ограниченной области по сравнению с ζ (2) , где ζ ( s ) — дзета-функция Римана .
Ссылки [ править ]
- ^ Whittaker & Watson 1927 , Приложение .
- ^ Уиттакер и Уотсон 1927 , с. 10.
- ^ Вайсштейн, Эрик В. (8 февраля 2024 г.). «Диаграмма Аргана» . Математический мир . Проверено 17 февраля 2024 г.
- ^ Уиттакер и Уотсон 1927 , с. 9.
- ^ Фланиган 1983 , с. 305.
- ↑ Перейти обратно: Перейти обратно: а б Моретти 1964 , стр. 113–119.
- ^ Уиттакер и Уотсон 1927 , стр. 235–236.
- ^ Стена 1948 , с. 39.
Цитируемые работы [ править ]
- Фланиган, Фрэнсис Дж. (1983). Комплексные переменные: гармонические и аналитические функции . Дувр. ISBN 0-486-61388-7 .
- Моретти, Джино (1964). Функции комплексной переменной . Прентис-Холл.
- Уолл, HS (1948). Аналитическая теория цепных дробей . Компания Д. Ван Ностранда. Перепечатано (1973) издательством Chelsea Publishing Company. ISBN 0-8284-0207-8 .
- Уиттакер, ET ; Уотсон, Дж. Н. (1927). Курс современного анализа (Четвертое изд.). Издательство Кембриджского университета.
Внешние ссылки [ править ]
- Жан-Робер Арган, « Очерк о способах представления мнимых величин в геометрических конструкциях », 1806 г., онлайн и проанализирован на BibNum [для английской версии нажмите « чтобы скачать »]












![{\displaystyle \Gamma (z)={\frac {e^{-\gamma z}}{z}} \prod _ {n = 1}^{\infty }\left[\left(1+{\frac {z}{n}}\вправо)^{-1}e^{z/n}\вправо]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78a2a4c26802856b410866a0e00e4c5046664928)





