Набор Мандельброта

Набор Мандельброта в непрерывно окрашенной среде.

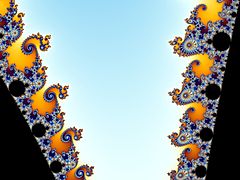
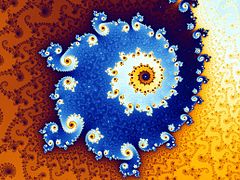
Множество Мандельброта ( / ˈ m æ n d əl b r oʊ t , - b r ɒ t / ) представляет собой двумерный набор с относительно простым определением, который демонстрирует большую сложность, особенно при увеличении. Он популярен благодаря своей эстетической привлекательности и фрактальным структурам. Множество определяется в комплексной плоскости как комплексные числа $c$ для которого функция $f_{c}(z)=z^{2}+c$ не уходит в бесконечность при повторении, начиная с $z=0$, т. е. для которого последовательность $f_{c}(0)$, $f_{c}(f_{c}(0))$и т. д., остается ограниченным по абсолютной величине .

Этот набор был впервые определен и нарисован Робертом Бруксом и Питером Мательски в 1978 году в рамках исследования кляйнианских групп . Впоследствии, в 1980 году, Бенуа Мандельброт получил высококачественные визуализации набора, работая в в IBM Исследовательском центре Томаса Дж. Уотсона Йорктаун -Хайтс, Нью-Йорк .

Увеличение масштаба границы множества Мандельброта

Изображения множества Мандельброта демонстрируют бесконечно сложную границу раскрывает все более мелкие рекурсивные , которая при увеличении детали; математически граница множества Мандельброта представляет собой фрактальную кривую . «Стиль» этой рекурсивной детали зависит от исследуемой области заданной границы. Изображения множества Мандельброта могут быть созданы путем выборки комплексных чисел и тестирования для каждой точки выборки. $c$, является ли последовательность $f_{c}(0),f_{c}(f_{c}(0)),\dotsc$ уходит в бесконечность . Работа с реальной и мнимой частями $c$ В качестве координат изображения на комплексной плоскости пиксели затем могут быть окрашены в зависимости от того, как скоро последовательность $|f_{c}(0)|,|f_{c}(f_{c}(0))|,\dotsc$ пересекает произвольно выбранный порог (порог должен быть не менее 2, поскольку -2 — это комплексное число с наибольшей величиной в наборе, в противном случае порог является произвольным). Если $c$ считается постоянным, а начальное значение $z$ вместо этого варьируется соответствующий набор Жюлиа для точки $c$ получается.

Множество Мандельброта стало популярным за пределами математики как из-за своей эстетической привлекательности, так и как пример сложной структуры, возникающей в результате применения простых правил. Это один из самых известных примеров математической визуализации , математической красоты и мотива .

История

Первое опубликованное изображение множества Мандельброта, сделанное Робертом В. Бруксом и Питером Мательски в 1978 году.

Множество Мандельброта берет свое начало в сложной динамике — области, впервые исследованной французскими математиками Пьером Фату и Гастоном Жюли в начале 20 века. Фрактал был впервые определен и нарисован в 1978 году Робертом Бруксом и Питером Мательски в рамках исследования кляйнианских групп . 1 марта 1980 года в IBM компании Исследовательском центре Томаса Дж. Уотсона в Йорктаун-Хайтс , штат Нью-Йорк , Бенуа Мандельброт впервые визуализировал этот набор.

Мандельброт изучил пространство параметров квадратичных многочленов в статье, появившейся в 1980 году. Математическое исследование множества Мандельброта действительно началось с работы математиков Адриана Дуади и Джона Х. Хаббарда (1985): который установил многие из его фундаментальных свойств и назвал множество в честь Мандельброта за его влиятельную работу во фрактальной геометрии .

Математики Хайнц-Отто Пейтген и Петер Рихтер стали известны тем, что продвигали набор с помощью фотографий, книг (1986), и международная гастрольная выставка немецкого Гете-Института (1985).

В обложке журнала Scientific American за август 1985 года был представлен алгоритм вычисления множества Мандельброта. Обложку создали Пайтген, Рихтер и Саупе в Бременском университете . Набор Мандельброта стал известен в середине 1980-х годов как демонстрация компьютерной графики , когда персональные компьютеры стали достаточно мощными, чтобы рисовать и отображать набор в высоком разрешении.

Работа Дуади и Хаббарда произошла во время роста интереса к сложной динамике и абстрактной математике . и с тех пор изучение множества Мандельброта стало центральным элементом этой области.

Формальное определение

Множество Мандельброта — это набор значений c в комплексной плоскости , для которых орбита критической точки ${\textstyle z=0}$ при итерации квадратичного отображения

$z_{n+1}=z_{n}^{2}+c$

остается ограниченным . Таким образом, комплексное число c является членом множества Мандельброта, если, начиная с $z_{0}=0$ и повторно применяя итерацию, значение абсолютное $z_{n}$ остается ограниченным для всех $n>0$.

Например, для c = 1 последовательность равна 0, 1, 2, 5, 26, ..., которая стремится к бесконечности , поэтому 1 не является элементом множества Мандельброта. С другой стороны, для $c=-1$, последовательность равна 0, −1, 0, −1, 0, ..., которая ограничена, поэтому −1 действительно принадлежит множеству.

Множество Мандельброта также можно определить как локус связности семейства квадратных многочленов. $f(z)=z^{2}+c$, подмножество пространства параметров $c$ для которого множество Жюлиа соответствующего многочлена образует связное множество . Точно так же границу множества Мандельброта можно определить как место бифуркации этого квадратичного семейства, подмножества параметров, вблизи которого динамическое поведение полинома (при его повторении ) резко меняется.

Основные свойства

Множество Мандельброта является компактным , так как оно замкнуто и содержится в замкнутом круге радиуса 2 вокруг начала координат . точка $c$ принадлежит множеству Мандельброта тогда и только тогда, когда $|z_{n}|\leq 2$ для всех $n\geq 0$. Другими словами, абсолютное значение $z_{n}$ должно оставаться на уровне 2 или ниже для $c$ находиться в множестве Мандельброта, $M$, и если это абсолютное значение превышает 2, последовательность уйдет в бесконечность. С $c=z_{1}$, отсюда следует, что $|c|\leq 2$, установив, что $c$ всегда будет находиться в замкнутом диске радиуса 2 вокруг начала координат.

Соответствие множества Мандельброта бифуркационной диаграмме квадратичного отображения

С $z_{n}$ итераций, нанесенных на вертикальную ось, можно увидеть, что множество Мандельброта раздваивается в периоде-2 ^к компоненты.

Пересечение ​ ​ $M$ с действительной осью — это интервал $\left[-2,{\frac {1}{4}}\right]$. Параметры в этом интервале можно привести во взаимно однозначное соответствие с параметрами реального логистического семейства .

$x_{n+1}=rx_{n}(1-x_{n}),\quad r\in [1,4].$

Переписка предоставлена

$z=r\left({\frac {1}{2}}-x\right),\quad c={\frac {r}{2}}\left(1-{\frac {r}{2}}\right).$

Это дает соответствие между всем пространством параметров логистического семейства и пространством множества Мандельброта.

Дуади и Хаббард показали, что множество Мандельброта связно . Они построили явный конформный изоморфизм между дополнением множества Мандельброта и дополнением замкнутого единичного круга . Первоначально Мандельброт предположил, что множество Мандельброта несвязно . Эта гипотеза была основана на компьютерных изображениях, созданных программами, которые не способны обнаружить тонкие нити, соединяющие разные части тела. $M$. В ходе дальнейших экспериментов он пересмотрел свою гипотезу, решив, что $M$ должен быть подключен. Топологическое доказательство связности было обнаружено в 2001 году Джереми Каном .

Внешние лучи следов вблизи континента периода 1 множества Мандельброта

Динамическая формула униформизации дополнения к множеству Мандельброта, возникшая на основе доказательства Дуади и Хаббарда связности $M$, порождает внешние лучи множества Мандельброта. Эти лучи можно использовать для изучения множества Мандельброта в комбинаторных терминах и сформировать основу параголоволомки Йоккоза .

Границей место множества Мандельброта является бифуркации семейства квадратичных многочленов. Другими словами, граница множества Мандельброта — это совокупность всех параметров $c$ для которого динамика квадратичного отображения $z_{n}=z_{n-1}^{2}+c$ проявляет чувствительную зависимость от $c,$ т.е. резко меняется при сколь угодно малых изменениях $c.$ Его можно построить как предельное множество последовательности плоских алгебраических кривых — кривых Мандельброта общего типа, известных как полиномиальные лемнискаты . Кривые Мандельброта определяются установкой $p_{0}=z,\ p_{n+1}=p_{n}^{2}+z$, а затем интерпретируем набор точек $|p_{n}(z)|=2$ в комплексной плоскости как кривая в вещественной декартовой плоскости степени $2^{n+1}$по х и у . Каждая кривая $n>0$ — отображение исходной окружности радиуса 2 при $p_{n}$. Эти алгебраические кривые появляются на изображениях множества Мандельброта, вычисленных с использованием упомянутого ниже «алгоритма времени выхода».

Другие объекты недвижимости

Основные кардиоидные и периодические лампы

Периоды гиперболических компонент

Основная кардиоида – это период 1 континента. Это область параметров $c$ для чего карта

$f_{c}(z)=z^{2}+c$

имеет притягивающую неподвижную точку . Он состоит из всех параметров вида

$c(\mu ):={\frac {\mu }{2}}\left(1-{\frac {\mu }{2}}\right)$

для некоторых $\mu$ в открытом блоке диск .

Слева от основной кардиоиды, прикрепленной к ней в точке $c=-3/4$, круглая лампочка, лампочка периода-2 видна . Лампа состоит из $c$ для чего $f_{c}$ имеет притягивающий цикл периода 2 . Это закрашенный круг радиуса 1/4 с центром вокруг −1.

В более общем смысле, для каждого положительного целого числа $q>2$, есть $\phi (q)$ круглые лампочки, касающиеся основной кардиоиды, называемые лампочками периода q (где $\phi$ обозначает фи-функцию Эйлера ), которые состоят из параметров $c$ для чего $f_{c}$ имеет притягивающий цикл периода $q$. Точнее, для каждого примитива $q$корень единства $r=e^{2\pi i{\frac {p}{q}}}$ (где $0<{\frac {p}{q}}<1$), есть одна лампочка с периодом q, называемая ${\frac {p}{q}}$ лампочка, касательная к основной кардиоиде при параметре

$c_{\frac {p}{q}}:=c(r)={\frac {r}{2}}\left(1-{\frac {r}{2}}\right),$

Притягивающий цикл в 2/5 лампочке, построенный на наборе Джулии (анимация)

и который содержит параметры с $q$-циклы, имеющие комбинаторное число вращения ${\frac {p}{q}}$. Точнее, $q$ периодические компоненты Фату, содержащие притягивающий цикл, соприкасаются в общей точке (обычно называемой $\alpha$-фиксированная точка ). Если мы обозначим эти компоненты $U_{0},\dots ,U_{q-1}$ против часовой стрелки, затем $f_{c}$ отображает компонент $U_{j}$ к компоненту $U_{j+p\,(\operatorname {mod} q)}$.

Притягивающие циклы и наборы Джулии для параметров лампочек 1/2, 3/7, 2/5, 1/3, 1/4 и 1/5.

Изменение поведения, происходящее $c_{\frac {p}{q}}$ известен как бифуркация : притягивающая неподвижная точка «сталкивается» с отталкивающим циклом периода q . Когда мы переходим через параметр бифуркации в ${\tfrac {p}{q}}$-лампочка, притягивающая неподвижная точка превращается в отталкивающую неподвижную точку (т. $\alpha$-фиксированная точка), и цикл периода q становится притягивающим.

Гиперболические компоненты

Лампочки, являющиеся внутренними компонентами множества Мандельброта, в котором карты $f_{c}$ имеют притягивающий периодический цикл, называются гиперболическими компонентами .

Предполагается, что это единственные внутренние области $M$ они плотные и что $M$. Эта проблема, известная как плотность гиперболичности , является одной из наиболее важных открытых проблем в сложной динамике . Гипотетические негиперболические компоненты множества Мандельброта часто называют «странными» или призрачными компонентами. Для действительных квадратичных полиномов этот вопрос был доказан в 1990-х годах независимо Любичем, а также Грачиком и Свёнтеком. (Обратите внимание, что гиперболические компоненты, пересекающие действительную ось, точно соответствуют периодическим окнам на диаграмме Фейгенбаума . Таким образом, этот результат утверждает, что такие окна существуют вблизи каждого параметра на диаграмме.)

Не к каждой гиперболической компоненте можно добраться последовательностью прямых бифуркаций от главной кардиоиды множества Мандельброта. К такому компоненту можно прийти последовательностью прямых бифуркаций от главной кардиоиды маленькой копии Мандельброта (см. ниже).

Центры 983 гиперболических компонент множества Мандельброта.

Каждая из гиперболических компонент имеет центр , который является точкой c такой, что внутренняя область Фату для $f_{c}(z)$ имеет цикл сверхпритяжения, то есть притяжение бесконечно. Это означает, что цикл содержит критическую точку 0, так что 0 после нескольких итераций возвращается к самому себе. Поэтому, $f_{c}^{n}(0)=0$ для некоторых н . Если мы назовем этот полином $Q^{n}(c)$ (позволяя этому зависеть от c вместо z ), мы имеем это $Q^{n+1}(c)=Q^{n}(c)^{2}+c$ и что степень $Q^{n}(c)$ является $2^{n-1}$. Поэтому построение центров гиперболических компонент возможно путем последовательного решения уравнений $Q^{n}(c)=0,n=1,2,3,...$. Количество новых центров, созданных на каждом этапе, определяется OEIS Слоана : A000740 .

Локальное подключение

Предполагается, что множество Мандельброта локально связно . Эта гипотеза известна как MLC (от локально связного Мандельброта ). Благодаря работе Адриана Дуади и Джона Х. Хаббарда эта гипотеза привела к созданию простой абстрактной модели «сжатого диска» множества Мандельброта. В частности, это подразумевало бы важную гипотезу гиперболичности, упомянутую выше.

Работа Жана-Кристофа Йоко установила локальную связность множества Мандельброта при всех конечно перенормируемых параметрах; то есть, грубо говоря, содержащиеся лишь в конечном числе маленьких копий Мандельброта. С тех пор локальная связность была доказана во многих других точках $M$, но полная гипотеза все еще остается открытой.

Самоподобие

Самоподобие в множестве Мандельброта показано увеличением круглого объекта при панорамировании в отрицательном направлении x . Центр дисплея перемещается влево от пятого к седьмому раунду от (-1,4002, 0) до (-1,4011, 0), а изображение увеличивается в 21,78 раза, чтобы приблизиться к квадрату отношения Фейгенбаума .

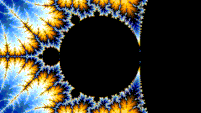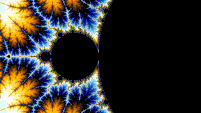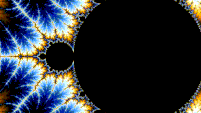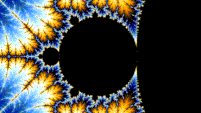
Множество Мандельброта самоподобно при увеличении в окрестностях точек Мисюревича . Также предполагается, что он самоподобен вокруг обобщенных точек Фейгенбаума (например, -1,401155 или -0,1528 + 1,0397 i ) в смысле сходимости к предельному множеству. Множество Мандельброта в целом квазисамоподобно, поскольку небольшие, слегка отличающиеся версии самого себя можно найти в сколь угодно малых масштабах. Все эти копии набора Мандельброта немного отличаются, в основном из-за тонких нитей, соединяющих их с основной частью набора.

Дальнейшие результаты

Хаусдорфова размерность границы множества Мандельброта равна 2, как это определено Мицухиро Шишикурой . Тот факт, что это число на целое число больше, чем его топологическая размерность, равная 1, отражает крайнюю фрактальную природу границы множества Мандельброта. Грубо говоря, результат Шишикуры утверждает, что граница множества Мандельброта настолько «волнистая», что локально заполняет пространство так же эффективно, как двумерная плоская область. Кривые с размерностью Хаусдорфа 2, несмотря на то, что они (топологически) одномерны, часто могут иметь ненулевую площадь (более формально, ненулевую плоскую меру Лебега ). Так ли обстоит дело с границей множества Мандельброта, остается нерешенной проблемой.

Было показано, что обобщенное множество Мандельброта в многомерных гиперкомплексных числовых пространствах (т.е. когда степень $\alpha$ повторяемой переменной $z$ стремится к бесконечности) сходится к единице ( $\alpha$-1)-сфера.

В Блюма-Шуба-Смейла модели реальных вычислений множество Мандельброта не вычислимо, но его дополнение вычислимо перечислимо . Многие простые объекты (например, график возведения в степень) также не вычислимы в модели BSS. В настоящее время неизвестно, вычислимо ли множество Мандельброта в моделях реальных вычислений, основанных на вычислимом анализе , которые более точно соответствуют интуитивному понятию «построение множества с помощью компьютера». Гертлинг показал, что множество Мандельброта вычислимо в этой модели, если гипотеза гиперболичности верна.

Отношения с Юлей налаживаются

Мозаика, созданная путем сопоставления наборов Джулии со значениями c на комплексной плоскости. Множество Мандельброта представляет собой карту связных множеств Жюлиа.

Как следствие определения множества Мандельброта, существует тесное соответствие между геометрией множества Мандельброта в данной точке и структурой соответствующего множества Жюлиа . Например, значение c принадлежит множеству Мандельброта тогда и только тогда, когда соответствующее множество Жюлиа связно. Таким образом, множество Мандельброта можно рассматривать как отображение связных множеств Жюлиа.

Этот принцип используется практически во всех глубоких результатах на множестве Мандельброта. Например, Шишикура доказал, что для плотного набора параметров на границе множества Мандельброта множество Жюлиа имеет хаусдорфову размерность два, а затем переносит эту информацию на плоскость параметров. Точно так же Йокко сначала доказал локальную связность множеств Жюлиа, а затем установил ее для множества Мандельброта с соответствующими параметрами.

Геометрия

Для каждого рационального числа ${\tfrac {p}{q}}$, где p и q , взаимно простые гиперболическая компонента периода q отделяется от основной кардиоиды в точке на краю кардиоиды, соответствующей внутреннему углу ${\tfrac {2\pi p}{q}}$. Часть множества Мандельброта, соединенная с основной кардиоидой в этой точке бифуркации, называется p / q -лимбом . Компьютерные эксперименты показывают, что диаметр конечности стремится к нулю, как ${\tfrac {1}{q^{2}}}$. Наилучшая известная на данный момент оценка — это неравенство Йоккоза, которое утверждает, что размер стремится к нулю, как ${\tfrac {1}{q}}$.

Член периода q будет иметь $q-1$ «усики» наверху его конечности. Период данной лампочки определяется путем подсчета этих антенн. Числитель числа вращения p находится путем нумерации каждой антенны против часовой стрелки от конечности от 1 до $q-1$ и найти, какая антенна самая короткая.

Пи в множестве Мандельброта

Пытаясь продемонстрировать, что толщина p / q -лимба равна нулю, Дэвид Болл в 1991 году провел компьютерный эксперимент, в котором вычислил количество итераций, необходимое для того, чтобы ряд разошелся для $z=-{\tfrac {3}{4}}+i\varepsilon$ ( $-{\tfrac {3}{4}}$ являющееся его местонахождением). Поскольку ряд не расходится при точном значении $z=-{\tfrac {3}{4}}$, количество требуемых итераций увеличивается с небольшим $\varepsilon$. Оказывается, умножив значение $\varepsilon$ с необходимым количеством итераций дает приближение $\pi$ это становится лучше для меньшего размера $\varepsilon$. Например, для $\varepsilon$ = 0,0000001, количество итераций 31415928, произведение 3,1415928. В 2001 году Аарон Клебанов доказал открытие Болла.

Последовательность Фибоначчи в множестве Мандельброта

Набор Мандельброта имеет фундаментальную кардиоидную форму, украшенную многочисленными лампочками, непосредственно прикрепленными к нему. Понимание расположения этих луковиц требует детального изучения границы множества Мандельброта. При увеличении масштаба конкретных частей с геометрической точки зрения появляется точная выводимая информация о местоположении внутри границы и соответствующем динамическом поведении параметров, взятых из связанных лампочек.

Итерация квадратичного полинома $f_{c}(z)=z^{2}+c$, где $c$ это параметр, полученный от одной из лампочек, прикрепленных к главной кардиоиде в множестве Мандельброта, приводит к созданию карт, показывающих притягивающие циклы определенного периода. $q$ и номер вращения $p/q$. В этом контексте цикл притяжения демонстрирует вращательное движение вокруг центральной фиксированной точки, совершая в среднем $p/q$ оборотов на каждой итерации.

Луковицы в множестве Мандельброта отличаются как циклами притяжения, так и геометрическими особенностями своей структуры. Каждая лампочка характеризуется прикрепленной к ней антенной, исходящей из точки соединения и имеющей определенное количество спиц, указывающих на ее период. Например, $2/5$ лампочка идентифицируется по циклу притяжения с числом оборотов $2/5$. Его характерная антенноподобная структура включает точку соединения, из которой выходят пять спиц. Среди этих спиц так называемая главная спица непосредственно прикреплена к $2/5$ лампочка, а «самая маленькая» неосновная спица расположена примерно $2/5$ поворота против часовой стрелки от главной спицы, что обеспечивает отличительную идентификацию как $2/5$-лампочка. Возникает вопрос: как определить, какая из этих спиц является «самой маленькой»? В теории внешних лучей, разработанной Дуади и Хаббардом. есть ровно два внешних луча, приземляющихся в корневой точке спутниковой гиперболической компоненты множества Мандельброта. Каждый из этих лучей имеет внешний угол, который удваивается по карте удвоения угла. $\theta \mapsto$ $2\theta$. Согласно этой теореме, когда два луча попадают в одну и ту же точку, никакие другие лучи между ними не могут пересечься. Таким образом, «размер» этой области измеряется путем определения длины дуги между двумя углами.

Если корневой точкой главной кардиоиды является точка возврата $c=1/4$, то основной кардиоидой является $0/1$-лампочка. Корневая точка любой другой лампочки — это точка, где эта лампочка крепится к основной кардиоиде. Это вызывает вопрос: какая луковица является самой большой между корневыми точками $0/1$ и $1/2$-лампочки? Это явно $1/3$-лампочка. И обратите внимание, что $1/3$ получается из двух предыдущих дробей сложением Фарея , т. е. сложением числителей и сложением знаменателей.

${\frac {0}{1}}$ $\oplus$ ${\frac {1}{2}}$$=$${\frac {1}{3}}$

Точно так же самая большая луковица между $1/3$ и $1/2$-лампочки - это $2/5$-лампочка, опять же подаренная дополнением Фейри.

${\frac {1}{3}}$ $\oplus$ ${\frac {1}{2}}$$=$${\frac {2}{5}}$

Самая большая луковица между $2/5$ и $1/2$-лампочка - это $3/7$-луковица, а самая большая луковица между $2/5$ и $1/3$-лампочки - это $3/8$-лампочка и так далее. Расположение луковиц в множестве Мандельброта следует замечательному образцу, определяемому деревом Фарея , структурой, охватывающей все рациональные числа между $0$ и $1$. Такое упорядочение располагает лампочки вдоль границы главной кардиоиды точно в соответствии с рациональными числами в единичном интервале .

Последовательность Фибоначчи в множестве Мандельброта

Начиная с $1/3$ лампочка вверху и продвигается к $1/2$ круге, последовательность разворачивается систематически: самая большая луковица между $1/2$ и $1/3$ является $2/5$, между $1/3$ и $2/5$ является $3/8$и так далее. Интересно, что знаменатели периодов круглых лампочек в последовательных масштабах множества Мандельброта соответствуют последовательности чисел Фибоначчи , последовательности, которая получается путем сложения двух предыдущих членов — 1, 2, 3, 5, 8, 13, 21. ..

Последовательность Фибоначчи проявляется в количестве спиральных рукавов в уникальном месте множества Мандельброта, зеркально отраженных сверху и снизу. Это уникальное расположение требует максимального количества итераций для детального фрактального изображения со сложными деталями, повторяющимися при увеличении масштаба.

Галерея изображений последовательности масштабирования

Граница множества Мандельброта показывает более сложные детали по мере приближения или увеличения изображения. Ниже приведен пример последовательности изображений, масштабируемой до выбранного значения c .

Увеличение последнего изображения относительно первого около 10 раз. ¹⁰ к 1. Относительно обычного компьютерного монитора он представляет собой сечение множества Мандельброта диаметром 4 миллиона километров.

• 
  Начинать. Множество Мандельброта с непрерывно окрашенной средой.
• 
  Зазор между «головой» и «телом», также называемый «долиной морского конька».
• 
  Слева двойные спирали, справа «морские коньки».
• 
  «Морской конёк» вверх тормашками

«Тело» морского конька состоит из 25 «спиц», состоящих из двух групп по 12 «спиц» в каждой и одной «спицы», соединяющейся с основной кардиоидой. Эти две группы можно отнести путем некоторой метаморфозы к двум «пальцам» «верха» множества Мандельброта; следовательно, количество «спиц» увеличивается от одного «морского конька» к другому на 2; «концентратор» — это точка Мисюревича . Между «верхней частью тела» и «хвостом» находится искаженная копия множества Мандельброта, называемая «спутником».

• 
  Центральная конечная точка «хвоста морского конька» также является точкой Мисюревича .
• 
  Часть «хвоста» – существует только один путь, состоящий из тонких структур, проходящих через весь «хвост». Этот зигзагообразный путь проходит через «ступицы» крупных объектов с 25 «спцами» на внутренней и внешней границе «хвоста»; таким образом, множество Мандельброта представляет собой односвязное множество, а это означает, что вокруг дыры нет островов и кольцевых дорог.
• 
  Спутник. Два «хвоста морского конька» являются началом серии концентрических корон со спутником в центре.
• 
  Каждая из этих корон состоит из одинаковых «хвостов морского конька»; их число увеличивается со степенью 2, что является типичным явлением в среде спутников. Уникальный путь к центру спирали проходит спутник от канавки кардиоиды к вершине «антенны» на «голове».
• 
  «Антенна» спутника. Имеется несколько спутников второго порядка.
• 
  «Долина морских коньков» спутника. Все структуры с самого начала появляются снова.
• 
  Двойные спирали и «морские коньки» — в отличие от второго изображения с самого начала, у них есть отростки, состоящие из структур типа «хвостов морского конька»; это демонстрирует типичное соединение n + 1 различных структур в среде спутников порядка n , здесь для простейшего случая n = 1.
• 
  Двойные спирали со сателлитами второго порядка – по аналогии с «морскими коньками», двойные спирали можно интерпретировать как метаморфозу «антенны».
• 
  Во внешней части приложений можно узнать островки сооружений; они имеют форму, подобную множествам Юлии J _c ; самый крупный из них можно найти в центре «двойного крючка» с правой стороны.
• 
  Часть «двойного крючка».
• 
  Острова.
• 
  Деталь одного острова.
• 
  Деталь спирали.

Острова на предпоследнем шаге кажутся состоящими из бесконечного числа частей, как и в случае соответствующего множества Жюлиа. $J_{c}$. Они соединены крошечными структурами, так что целое представляет собой односвязное множество. Крошечные структуры встречаются друг с другом на спутнике в центре, который слишком мал, чтобы его можно было распознать при таком увеличении. Стоимость $c$ для соответствующего $J_{c}$ не является центром изображения, но относительно основной части множества Мандельброта занимает то же положение, что и центр этого изображения относительно спутника, показанного на 6-м шаге.

Внутренняя структура

Хотя множество Мандельброта обычно визуализируется с отображением деталей внешних границ, также может быть выявлена ​​структура внутри ограниченного множества. Например, при вычислении того, является ли данное значение c связанным или несвязанным, пока оно остается связанным, максимальное значение, которого достигает это число, можно сравнить со значением c в этом месте. Если используется метод суммы квадратов, вычисленное число будет иметь вид max:(действительное^2 + мнимое^2) - c:(действительное^2 + мнимое^2). Величину этого расчета можно представить как значение градиента.

Это приводит к следующим результатам: градиенты с четкими краями и контурами по мере приближения к границам. Анимации служат для выделения границ градиента.

• 
  Анимированная структура градиента внутри множества Мандельброта
• 
  Анимированная структура градиента внутри множества Мандельброта, деталь
• 
  Рендеринг прогрессивных итераций от 285 до примерно 200 000 с анимированными соответствующими ограниченными градиентами.
• 
  Миниатюра градиента в прогрессивных итерациях

Обобщения

Duration: 10 seconds.0:10

Анимации набора Мультиброт для d от 0 до 5 (слева) и от 0,05 до 2 (справа).

4D-множество Жюлиа можно спроецировать или разделить на 3D, поэтому также возможно 4D-множество Мандельброта.

Наборы Мультиброт

Мультибротные множества - это ограниченные множества, найденные в комплексной плоскости для членов общего семейства одномерных полиномиальных рекурсий.

$z\mapsto z^{d}+c$.

Для целого числа d эти наборы являются локусами связности для множеств Жюлиа, построенных по той же формуле. Также был изучен локус полной кубической связности; здесь рассматривается двухпараметрическая рекурсия $z\mapsto z^{3}+3kz+c$, две критические точки которого являются комплексными квадратными корнями параметра k . Параметр находится в локусе кубической связности, если обе критические точки стабильны. Для общих семейств голоморфных функций граница множества Мандельброта обобщается до бифуркационного локуса .

получается Множество Мультибро путем изменения значения показателя d . В статье есть видео, где показано развитие от d =0 до 7, в этот момент их 6 т.е. $(d-1)$ лепестки по периметру . В общем, когда d — целое положительное число, центральная область в каждом из этих множеств всегда эпициклоидой является $(d-1)$ выступы. Аналогичное развитие событий с отрицательными целыми показателями приводит к $(1-d)$ расщелины на внутренней стороне кольца, где основная центральная область множества представляет гипоциклоиду собой $(1-d)$ выступы.

Высшие измерения

Не существует идеального расширения множества Мандельброта в 3D, потому что не существует 3D-аналога комплексных чисел, по которому можно было бы выполнять итерации. Существует расширение комплексных чисел в 4 измерения, кватернионы , которые создают идеальное расширение множества Мандельброта и множеств Жюлиа в 4 измерения. Затем их можно либо разрезать в поперечном сечении , либо спроецировать в трехмерную структуру. Кватернионное (4-мерное) множество Мандельброта представляет собой просто тело вращения 2-мерного множества Мандельброта (в плоскости jk), и поэтому на него неинтересно смотреть. Взяв трехмерное сечение при $d=0\ (q=a+bi+cj+dk)$ приводит к телу вращения двумерного множества Мандельброта вокруг действительной оси.

Другие неаналитические сопоставления

Изображение фрактала Треуголка/Мандельбара

Особый интерес представляет фрактал- треугольник — локус связности антиголоморфного семейства.

$z\mapsto {\bar {z}}^{2}+c$.

Треуголка (также иногда называемая Мандельбаром ) была встречена Милнором в его исследовании срезов параметров действительных кубических многочленов . Он не подключен локально. Это свойство наследуется локусом связности вещественных кубических многочленов.

Еще одним неаналитическим обобщением является фрактал «Горящий корабль» , который получается повторением следующего:

$z\mapsto (|\Re \left(z\right)|+i|\Im \left(z\right)|)^{2}+c$.

Компьютерные рисунки

Основная статья: Алгоритмы построения множества Мандельброта

Существует множество различных алгоритмов построения множества Мандельброта с помощью вычислительного устройства. Здесь будет продемонстрирован наиболее широко используемый и простой алгоритм, а именно, наивный «алгоритм времени выхода». В алгоритме времени выхода повторяющийся расчет выполняется для каждой точки x , y в области графика, и на основе поведения этого расчета для этого пикселя выбирается цвет.

Местоположение x и y каждой точки используется в качестве начальных значений в повторяющихся или итерирующих вычислениях (подробно описано ниже). Результат каждой итерации используется в качестве начального значения для следующей. Значения проверяются во время каждой итерации, чтобы увидеть, достигли ли они критического состояния «выхода» или «катастрофы». Если это условие достигнуто, расчет останавливается, пиксель рисуется и x , y исследуется следующая точка .

Цвет каждой точки показывает, насколько быстро значения достигли точки выхода. Часто черный цвет используется для отображения значений, которые не могут выйти за пределы итерации, а для точек, которые выходят за рамки, постепенно используются более яркие цвета. Это дает визуальное представление о том, сколько циклов потребовалось для достижения условия выхода.

Для визуализации такого изображения рассматриваемую нами область комплексной плоскости разбивают на определенное количество пикселей . Чтобы раскрасить любой такой пиксель, пусть $c$ быть серединой этого пикселя. Повторите критическую точку 0 под $f_{c}$, проверяя на каждом шаге, имеет ли точка орбиты радиус больше 2. В этом случае $c$ не принадлежит множеству Мандельброта, и раскрасьте пиксель в соответствии с количеством итераций, использованных для его определения. В противном случае продолжайте итерацию до фиксированного количества шагов, после чего мы решаем, что наш параметр «вероятно» принадлежит множеству Мандельброта или, по крайней мере, очень близок к нему, и окрашиваем пиксель в черный цвет.

В псевдокоде этот алгоритм будет выглядеть следующим образом. Алгоритм не использует комплексные числа и вручную моделирует операции с комплексными числами, используя два действительных числа, для тех, у кого нет сложного типа данных . Программа может быть упрощена, если язык программирования включает операции со сложными типами данных .

for each pixel (Px, Py) on the screen do
    x0 := scaled x coordinate of pixel (scaled to lie in the Mandelbrot X scale (-2.00, 0.47))
    y0 := scaled y coordinate of pixel (scaled to lie in the Mandelbrot Y scale (-1.12, 1.12))
    x := 0.0
    y := 0.0
    iteration := 0
    max_iteration := 1000
    while (x^2 + y^2 ≤ 2^2 AND iteration < max_iteration) do
        xtemp := x^2 - y^2 + x0
        y := 2*x*y + y0
        x := xtemp
        iteration := iteration + 1

    color := palette[iteration]
    plot(Px, Py, color)

Здесь, связывая псевдокод с $c$, $z$ и $f_{c}$:

• $z=x+iy$
• $z^{2}=x^{2}+i2xy-y^{2}$
• $c=x_{0}+iy_{0}$

и так, как видно из псевдокода при вычислении x и y :

• $x=\mathop {\mathrm {Re} } (z^{2}+c)=x^{2}-y^{2}+x_{0}$ и $y=\mathop {\mathrm {Im} } (z^{2}+c)=2xy+y_{0}$.

Чтобы получить красочные изображения множества, присвоение цвета каждому значению числа выполненных итераций может быть произведено с помощью одной из множества функций (линейной, экспоненциальной и т. д.).

Упоминания в популярной культуре

Множество Мандельброта широко считается самым популярным фракталом . и несколько раз упоминался в популярной культуре .

• Песня Джонатана Коултона «Mandelbrot Set» — это дань уважения как самому фракталу, так и человеку, в честь которого он назван, Бенуа Мандельброту.
• на дебютном альбоме Blue Man Group 1999 года Audio Несколько названий треков относятся к сету Мандельброта. Это «Открытие Мандельброта», «Мандельгрув» и «Кляйн Мандельброт».
• Вторая книга серии Mode Пирса Энтони , Fractal Mode , описывает мир, который представляет собой идеальную 3D-модель набора.
• Артура Кларка В романе «Призрак с Гранд-Бэнкс» изображено искусственное озеро, повторяющее форму множества Мандельброта.
• Бенуа Мандельброт и одноименная компания стали героями дудла Google 20 ноября 2020 года (96-летие покойного Бенуа Мандельброта).
• Американская рок-группа Heart разместила изображение Мандельброта на обложке своего альбома 2004 года Jupiters Darling .
• Британская блэк-метал группа Anaal Nathrakh использует изображение, напоминающее набор Мандельброта, на Eschaton . обложке своего альбома
• В телесериале «Холистическое детективное агентство Дирка Джентли» (2016) заметно показано действие Мандельброта в связи с видениями персонажа Аманды. Во втором сезоне на ее куртке на спине большое изображение фрактала.
• В книге Яна Стюарта 2001 года «Флаттерланд» есть персонаж по имени Мандельблот, который помогает героям и читателю объяснять фракталы.
• Незавершенная Алана Мура серия комиксов 1990 года «Большие числа» использовала работы Мандельброта по фрактальной геометрии и теории хаоса в качестве основы для структуры этой работы. В какой-то момент Мур собирался назвать серию комиксов « множество Мандельброта» .
• В манге The Summer Hikaru Died Йошики галлюцинирует набор Мандельброта, когда он проникает в тело ложного Хикару.

См. также

• Буддадброт
• Фрактал Коллатца
• Фрактинт
• Перестановка Гилбрета
• Мандельбокс
• Мандельбулба
• Моя губка
• Ньютон фрактал
• Орбитальный портрет
• Орбитальная ловушка
• Пиковерный стебель
• Алгоритмы построения множества Мандельброта

Дальнейшее чтение

• Милнор, Джон В. (2006). Динамика в одной комплексной переменной . Анналы математических исследований. Том. 160 (Третье изд.). Издательство Принстонского университета. ISBN  0-691-12488-4 .
  (Впервые появилось в 1990 году как препринт Stony Brook IMS , доступный как arXiV:math.DS/9201272 )
• Лесмуар-Гордон, Найджел (2004). Цвета бесконечности: красота, сила и смысл фракталов . Очистить Пресс. ISBN  1-904555-05-5 .
  (включает DVD с участием Артура Кларка и Дэвида Гилмора )
• Пейтген, Хайнц Отто ; Юргенс, Хартмут ; Саупе, Дитмар (2004) [1992]. Хаос и фракталы: новые рубежи науки . Нью-Йорк: Спрингер. ISBN  0-387-20229-3 .

Внешние ссылки

• Хаос и фракталы в Керли
• Видео: Фрактальный зум Мандельброта до 6,066 e228
• Относительно простое объяснение математического процесса , автор : Холли Кригер , Массачусетский технологический институт.
• Обозреватель множеств Мандельброта : средство просмотра множеств Мандельброта на основе браузера с интерфейсом, похожим на карту.
• Различные алгоритмы вычисления множества Мандельброта (на Rosetta Code )
• Фрактальный калькулятор, написанный на Lua Деяном Добромировым, София, Болгария