Комплексный квадратичный полином

Комплексный квадратичный многочлен — это квадратный многочлен которого , коэффициенты и переменная являются комплексными числами .

Характеристики

Квадратичные полиномы независимо от формы обладают следующими свойствами:

• Это некритический полином, т. е. он имеет одну конечную критическую точку в комплексной плоскости. Динамическая плоскость состоит максимум из двух бассейнов: бассейна бесконечности и бассейна конечной критической точки (если конечная критическая точка не выходит за пределы)
• Она может быть посткритически конечной , т. е. орбита критической точки может быть конечной, поскольку критическая точка является периодической или предпериодической.
• Это унимодальная функция ,
• Это рациональная функция ,
• Это целая функция .

Формы

Когда квадратичный полином имеет только одну переменную ( одномерную ), можно выделить четыре его основные формы:

• Общая форма: $f(x)=a_{2}x^{2}+a_{1}x+a_{0}$ где $a_{2}\neq 0$
• Факторизованная форма, используемая для логистической карты : $f_{r}(x)=rx(1-x)$
• $f_{\theta }(x)=x^{2}+\lambda x$ который имеет безразличную неподвижную точку с множителем $\lambda =e^{2\pi \theta i}$ в начале
• Моническая , и центрированная форма $f_{c}(x)=x^{2}+c$

Уническая и центрированная форма широко изучена и обладает следующими свойствами:

• Это простейшая форма нелинейной функции с одним коэффициентом ( параметром ),
• Это центрированный полином (сумма его критических точек равна нулю).
• это бином

Лямбда-форма $f_{\lambda }(z)=z^{2}+\lambda z$ является:

• простейшее нетривиальное возмущение невозмущенной системы $z\mapsto \lambda z$
• «первое семейство динамических систем , в котором известны явные необходимые и достаточные условия, когда проблема малых делителей устойчива»

Спряжение

Между формами

С $f_{c}(x)$ аффинно сложной сопряжен с общей формой квадратичного многочлена; он часто используется для изучения динамики и создания изображений множеств Мандельброта , Жюлиа и Фату .

Когда человек хочет перемен от $\theta$ к $c$:

$c=c(\theta )={\frac {e^{2\pi \theta i}}{2}}\left(1-{\frac {e^{2\pi \theta i}}{2}}\right).$

Когда человек хочет перемен от $r$ к $c$, преобразование параметра

$c=c(r)={\frac {1-(r-1)^{2}}{4}}=-{\frac {r}{2}}\left({\frac {r-2}{2}}\right)$

и преобразование между переменными в $z_{t+1}=z_{t}^{2}+c$ и $x_{t+1}=rx_{t}(1-x_{t})$ является

$z=r\left({\frac {1}{2}}-x\right).$

С удвоенной картой

Существует полусопряженность между диадическим преобразованием (отображением удвоения) и случаем квадратичного полинома c = –2.

Обозначения

Итерация

Здесь $f^{n}$ обозначает n -ю итерацию функции $f$:

$f_{c}^{n}(z)=f_{c}^{1}(f_{c}^{n-1}(z))$

так

$z_{n}=f_{c}^{n}(z_{0}).$

Из-за возможной путаницы с возведением в степень некоторые авторы пишут $f^{\circ n}$ для n- й итерации $f$.

Параметр

Моническая и центрированная форма $f_{c}(x)=x^{2}+c$ можно обозначить:

• параметр $c$
• внешний угол $\theta$ луча, который приземляется:
  • в c в Мандельброте, заданном на плоскости параметров
  • от критического значения: z = c в наборе Жюлиа на динамической плоскости

так :

$f_{c}=f_{\theta }$

$c=c({\theta })$

Примеры:

• c — точка приземления 1/6 внешнего луча множества Мандельброта , и $z\to z^{2}+i$ (где я^2=-1)
• c — точка приземления внешнего луча 5/14 . $z\to z^{2}+c$ с $c=-1.23922555538957+0.412602181602004*i$

• 
  1/4
• 
  1/6
• 
  9/56
• 
  129/16256

Карта

Моническая и центрированная форма, иногда называемая семейством квадратичных многочленов Дуади-Хаббарда , обычно используется с переменной $z$ и параметр $c$:

$f_{c}(z)=z^{2}+c.$

Когда он используется как функция эволюции дискретной нелинейной динамической системы

$z_{n+1}=f_{c}(z_{n})$

оно называется квадратичным отображением :

$f_{c}:z\to z^{2}+c.$

Множество Мандельброта — это набор значений параметра c, для которых начальное условие z ₀ = 0 не приводит к расхождению итераций к бесконечности.

Критические предметы

Критические точки

сложная плоскость

точка Критическая ​ $f_{c}$ это точка $z_{cr}$ на динамической плоскости так, что производная обращается в нуль:

$f_{c}'(z_{cr})=0.$

С

$f_{c}'(z)={\frac {d}{dz}}f_{c}(z)=2z$

подразумевает

$z_{cr}=0,$

мы видим, что единственная (конечная) критическая точка $f_{c}$ в этом суть $z_{cr}=0$.

$z_{0}$ является начальной точкой для итерации множества Мандельброта .

Для квадратичного семейства $f_{c}(z)=z^{2}+c$ критическая точка z = 0 является центром симметрии множества Жюлиа Jc, поэтому она представляет собой выпуклую комбинацию двух точек из Jc.

расширенная сложная плоскость

В сфере Римана полином имеет 2d-2 критических точки. Здесь ноль и бесконечность являются критическими точками.

Критическое значение

Критическое значение $z_{cv}$ из $f_{c}$ является изображением критической точки:

$z_{cv}=f_{c}(z_{cr})$

С

$z_{cr}=0$

у нас есть

$z_{cv}=c$

Таким образом, параметр $c$ является критическим значением $f_{c}(z)$.

Кривые критического уровня

Кривая критического уровня – кривая уровня, содержащая критическую точку. Он действует как своего рода скелет. динамической плоскости

Пример: кривые уровня пересекаются в седловой точке , которая является особым типом критической точки.

• 
  привлечение
• 
  привлечение
• 
  привлечение
• 
  параболический
• Видео для c по внутреннему лучу 0

Установлен критический предел

Набор критических пределов - это набор прямых орбит всех критических точек.

Критическая орбита

Динамическая плоскость с критической орбитой, попадающая в трехпериодный цикл

Динамическая плоскость с множеством Жюлиа и критической орбитой.

Динамическая плоскость: изменения критической орбиты вдоль внутреннего луча главной кардиоиды на угол 1/6.

Критическая орбита, стремящаяся к слабо притягивающей неподвижной точке с abs(множителем) = 0,99993612384259

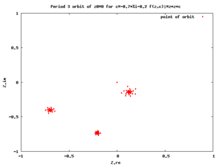
Передняя орбита критической точки называется критической орбитой . Критические орбиты очень важны, поскольку каждая притягивающая периодическая орбита притягивает критическую точку, поэтому изучение критических орбит помогает нам понять динамику множества Фату .

$z_{0}=z_{cr}=0$

$z_{1}=f_{c}(z_{0})=c$

$z_{2}=f_{c}(z_{1})=c^{2}+c$

$z_{3}=f_{c}(z_{2})=(c^{2}+c)^{2}+c$

$\ \vdots$

Эта орбита попадает в притягивающий периодический цикл, если таковой существует.

Критический сектор

Критический сектор – это сектор динамической плоскости, содержащий критическую точку.

Критический набор

Критический набор – это набор критических точек.

Критический полином

$P_{n}(c)=f_{c}^{n}(z_{cr})=f_{c}^{n}(0)$

так

$P_{0}(c)=0$

$P_{1}(c)=c$

$P_{2}(c)=c^{2}+c$

$P_{3}(c)=(c^{2}+c)^{2}+c$

Эти полиномы используются для:

• нахождение центров этих компонент множества Мандельброта периода n . Центры являются корнями -го n критического полинома.

${\text{centers}}=\{c:P_{n}(c)=0\}$

• нахождение корней компонентов множества Мандельброта периода n ( локальный минимум $P_{n}(c)$)
• Мисюревич очки

$M_{n,k}=\{c:P_{k}(c)=P_{k+n}(c)\}$

Критические кривые

Критические кривые

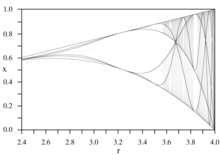
Диаграммы критических полиномов называются критическими кривыми .

Эти кривые создают скелет (темные линии) бифуркационной диаграммы .

Пространства, плоскости

4D пространство

можно использовать четырехмерное ( 4D) пространство Джулии-Мандельброта. Для глобального анализа этой динамической системы

w -плоскость и c -плоскость

В этом пространстве есть два основных типа 2D-плоскостей:

• динамическая (динамическая) плоскость, $f_{c}$-плоскость или c -плоскость
• плоскость параметров или z -плоскость

Существует также еще одна плоскость, используемая для анализа таких динамических систем w -плоскость :

• плоскость сопряжения
• модель самолета

2D-плоскость параметров

• Типы плоскостей параметров
• 
  плоскость параметров r (логистическая карта)
• 
  плоскость параметров c

Фазовое пространство квадратичного отображения называется плоскостью его параметров . Здесь:

$z_{0}=z_{cr}$ является постоянным и $c$ является переменной.

Никакой динамики здесь нет. Это всего лишь набор значений параметров. На плоскости параметров нет орбит.

Плоскость параметров состоит из:

• Множество Мандельброта
  • Место бифуркации = граница множества Мандельброта с
    • корневые точки
  • Ограниченные гиперболические компоненты множества Мандельброта = внутренняя часть множества Мандельброта. с внутренними лучами
• внешний вид набора Мандельброта с
  • внешние лучи
  • эквипотенциальные линии

Существует много различных подтипов плоскости параметров.

Карта множителей

См. также:

• Карта Бетчера , которая отображает внешнюю часть набора Мандельброта на внешнюю сторону единичного диска.
• карта множителя, которая отображает внутреннюю часть гиперболической компоненты множества Мандельброта во внутреннюю часть единичного круга

2D-динамическая плоскость

«Многочлен Pc отображает каждый динамический луч в другой луч, удваивая угол (который мы измеряем при полных оборотах, т.е. 0 = 1 = 2π рад = 360°), и динамические лучи любого многочлена «выглядят как прямые лучи» вблизи бесконечности. Это позволяет нам изучать множества Мандельброта и Жюлиа комбинаторно, заменяя динамическую плоскость единичным кругом, лучи углами, а квадратичный полином отображением удвоения по модулю один». Вирпи Кауко

В динамической плоскости можно найти:

• Набор Юлии
• Набор « Наполненная Джулия»
• Набор Фату
• Орбиты

Динамическая плоскость состоит из:

• Фату набор
• Джулия сет

Здесь, $c$ является константой и $z$ является переменной.

Двумерную динамическую плоскость можно рассматривать как сечение Пуанкаре трехмерного пространства непрерывной динамической системы.

Динамические z -плоскости можно разделить на две группы:

• $f_{0}$ самолет для $c=0$ (см. карту комплексного возведения в квадрат )
• $f_{c}$ самолеты (все остальные самолеты для $c\neq 0$)

сфера Римана

Расширенная комплексная плоскость плюс бесконечная точка.

• сфера Римана

Производные

Первая производная по c

На плоскости параметров:

• $c$ это переменная
• $z_{0}=0$ постоянен

Первая производная от $f_{c}^{n}(z_{0})$ относительно c есть

$z_{n}'={\frac {d}{dc}}f_{c}^{n}(z_{0}).$

Эту производную можно найти итерацией, начиная с

$z_{0}'={\frac {d}{dc}}f_{c}^{0}(z_{0})=1$

а затем заменяя на каждом последовательном шаге

$z_{n+1}'={\frac {d}{dc}}f_{c}^{n+1}(z_{0})=2\cdot {}f_{c}^{n}(z)\cdot {\frac {d}{dc}}f_{c}^{n}(z_{0})+1=2\cdot z_{n}\cdot z_{n}'+1.$

В этом легко убедиться, воспользовавшись цепным правилом для производной.

Эта производная используется в методе оценки расстояния для построения множества Мандельброта .

Первая производная по z

В динамической плоскости:

• $z$ является переменной;
• $c$ является константой.

В фиксированной точке $z_{0}$,

$f_{c}'(z_{0})={\frac {d}{dz}}f_{c}(z_{0})=2z_{0}.$

В периодической точке z ₀ периода p первая производная функции

$(f_{c}^{p})'(z_{0})={\frac {d}{dz}}f_{c}^{p}(z_{0})=\prod _{i=0}^{p-1}f_{c}'(z_{i})=2^{p}\prod _{i=0}^{p-1}z_{i}=\lambda$

часто представлен $\lambda$ и называется множителем или характеристическим числом Ляпунова. Его логарифм известен как показатель Ляпунова. Абсолютное значение множителя используется для проверки устойчивости периодических (также фиксированных) точек .

В непериодической точке производная, обозначаемая $z'_{n}$, можно найти путем итерации, начиная с

$z'_{0}=1,$

а затем используя

$z'_{n}=2*z_{n-1}*z'_{n-1}.$

Эта производная используется для вычисления внешнего расстояния до множества Жюлиа.

Производная Шварца

Производная Шварца (сокращенно SD) от f равна:

$(Sf)(z)={\frac {f'''(z)}{f'(z)}}-{\frac {3}{2}}\left({\frac {f''(z)}{f'(z)}}\right)^{2}.$

См. также

• точка Мисюревича
• Периодические точки комплексных квадратичных отображений
• Набор Мандельброта
• Джулия сет
• Теория замешивания Милнора – Терстона
• Карта палаток
• Логистическая карта

Внешние ссылки

• Моника Невинс и Томас Д. Роджерс, « Квадратичные карты как динамические системы p-адических чисел». "
• Вольф Юнг: Гомеоморфизмы на ребрах множества Мандельброта. доктор философии дипломная работа 2002 г.
• Подробнее о квадратичных картах: Квадратичная карта