Вращательно-колебательная спектроскопия

Вращательно-колебательная спектроскопия раздел молекулярной спектроскопии , изучающий инфракрасные и рамановские спектры молекул — в газовой фазе . Переходы, включающие изменения как в колебательном , так и в вращательном состояниях, могут быть сокращенно обозначены как вращательно-колебательные (или вращательно-колебательные ) переходы. Когда такие переходы испускают или поглощают фотоны ( электромагнитное излучение ), частота пропорциональна разнице энергетических уровней и может быть обнаружена с помощью определенных видов спектроскопии . Поскольку изменения уровней вращательной энергии обычно намного меньше, чем изменения уровней колебательной энергии, говорят, что изменения вращательного состояния придают тонкую структуру колебательному спектру. Для данного колебательного перехода та же теоретическая трактовка, что и для чистой вращательной спектроскопии, дает вращательные квантовые числа , уровни энергии и правила отбора . В молекулах с линейной и сферической вершиной линии вращения обнаруживаются как простые прогрессии как на более высоких, так и на более низких частотах относительно чистой частоты вибрации. В молекулах с симметричным волчком переходы классифицируются как параллельные, если Изменение дипольного момента параллельно главной оси вращения и перпендикулярно, если изменение перпендикулярно этой оси. асимметричного ротора Ро-колебательный спектр воды важен из-за присутствия водяного пара в атмосфере.

Обзор

См. Также: Вращательная спектроскопия и Вибронная спектроскопия.

Ро-колебательная спектроскопия касается молекул в газовой фазе . Существуют последовательности квантованных вращательных уровней, связанных как с основным, так и с возбужденным колебательными состояниями. Спектры часто разрешаются в линии из-за переходов с одного вращательного уровня в основном колебательном состоянии на один вращательный уровень в колебательно-возбужденном состоянии. Линии, соответствующие данному колебательному переходу, образуют полосу .

В простейших случаях часть инфракрасного спектра, включающая колебательные переходы с одинаковым вращательным квантовым числом (ΔJ = 0) в основном и возбужденном состояниях, называется Q-ветвью. На высокочастотной стороне Q-ветви к энергии колебательного перехода добавляется энергия вращательных переходов. Это известно как R-ветвь спектра для ΔJ = +1. P-ветвь для ΔJ = −1 лежит со стороны Q-ветви с низким волновым числом. Внешний вид R-ветви очень похож на внешний вид чистого спектра вращения (но сдвинут в сторону гораздо более высоких волновых чисел ), а P-ветвь выглядит как почти зеркальное отражение R-ветви. Ветвь Q иногда отсутствует, поскольку запрещены переходы без изменения J.

Появление вращательной тонкой структуры определяется симметрией молекулярных роторов , которые классифицируются так же, как и в чисто вращательной спектроскопии, на классы линейных молекул, сферических, симметричных и асимметричных роторов. Квантовомеханическая трактовка вращательной тонкой структуры такая же, как и для чистого вращения .

Сила линии поглощения связана с количеством молекул с начальными значениями колебательного квантового числа ν и вращательного квантового числа. $J$, и зависит от температуры. Поскольку на самом деле существуют $2J+1$ состояния с вращательным квантовым числом $J$, население со значением $J$ увеличивается с $J$ сначала, а затем затухает при более высоких $J$. Это придает характерную форму ветвям P и R.

Общее соглашение состоит в том, чтобы обозначать величины, относящиеся к основному и возбужденному состояниям перехода, двойным штрихом и одинарным штрихом соответственно. Например, постоянная вращения для основного состояния записывается как $B^{\prime \prime },$ и состояние возбужденного состояния как $B^{\prime }.$Кроме того, эти константы выражаются в единицах молекулярной спектроскопии см. ⁻¹ . так что $B$ в этой статье соответствует ${\bar {B}}=B/hc$ в определении постоянной вращения жесткого ротора .

Метод комбинаций разностей

Численный анализ вращательно-колебательных спектральных данных может показаться сложным из-за того, что волновое число для каждого перехода зависит от двух вращательных постоянных: $B^{\prime \prime }$ и $B^{\prime }$. Однако комбинации, которые зависят только от одной вращательной постоянной, находятся путем вычитания волновых чисел пар линий (одной в P-ветви и одной в R-ветви), которые имеют либо одинаковый нижний уровень, либо один и тот же верхний уровень. Например, в двухатомной молекуле линия, обозначенная P ( J +1), обусловлена ​​переходом ( v = 0, J +1) → ( v = 1, J ) (имеется в виду переход из состояния с колебательным квантовым числом ν от 0 до 1, а вращательное квантовое число переходит от некоторого значения J + 1 к J , при этом J > 0), а линия R ( J − 1) обусловлена ​​переходом ( v = 0, J − 1) → ( v = 1, Дж ). Разница между двумя волновыми числами соответствует разнице энергий между уровнями ( J + 1) и ( J - 1) нижнего колебательного состояния и обозначается $\Delta _{2}$ поскольку это разница между уровнями, отличающимися на две единицы Дж. Если учитывать центробежное искажение, оно определяется выражением

$\Delta _{2}^{\prime \prime }F(J)={\bar {\nu }}(R(J-1))-{\bar {\nu }}(P(J+1))=(2B^{\prime \prime }-3D^{\prime \prime })\left(2J+1\right)-D^{\prime \prime }\left(2J+1\right)^{3}$

где ${\bar {\nu }}()$ означает частоту (или волновое число ) данной линии. Основной термин, $2B''(2J+1),$ возникает из-за разницы в энергии $J+1$ вращательное состояние, $B''((J+1)(J+2)),$ и что из $J-1$ состояние, $B''((J-1)J).$

Постоянная вращения основного колебательного состояния B " и константа центробежного искажения D " могут быть найдены методом наименьших квадратов, эту разницу как функцию J. подгоняющим Константа B » используется для определения межъядерного расстояния в основном состоянии, как и в чистой вращательной спектроскопии . (См. Приложение )

Аналогично, разность R ( J ) − P ( J ) зависит только от констант B ′ и D ′ для возбужденного колебательного состояния ( v = 1), и B ′ может использоваться для определения межъядерного расстояния в этом состоянии (которое недоступны для чистой вращательной спектроскопии).

$\Delta _{2}^{\prime }F(J)={\bar {\nu }}(R(J))-{\bar {\nu }}(P(J))=(2B^{\prime }-3D^{\prime })\left(2J+1\right)-D^{\prime }\left(2J+1\right)^{3}$

Линейные молекулы

Гетероядерные двухатомные молекулы

Имитированный вибро-вращательный линейный спектр монооксида углерода , ¹² С ¹⁶ О. П-ветвь левее разрыва около 2140 см. ⁻¹ , R-ветвь справа.

Схематическая диаграмма колебательно-энергетических уровней линейной молекулы

Двухатомные молекулы общей формулы AB имеют один нормальный режим колебаний, связанный с растяжением связи AB. Значения вибрационного члена $G(v)$, для ангармонического осциллятора в первом приближении даются формулами

$G(v)=\omega _{e}\left(v+{1 \over 2}\right)-\omega _{e}\chi _{e}\left(v+{1 \over 2}\right)^{2}\,$

где v — колебательное квантовое число , ω _e — волновое число гармоники, а χ _e — константа ангармонизма.

Когда молекула находится в газовой фазе, она может вращаться вокруг оси, перпендикулярной оси молекулы, проходящей через центр масс молекулы. Энергия вращения также квантуется, при этом значения членов в первом приближении определяются выражением

$F_{v}(J)=B_{v}J\left(J+1\right)-DJ^{2}\left(J+1\right)^{2}$

где J — вращательное квантовое число, а D — константа центробежного искажения . Постоянная вращения B _v зависит от момента инерции молекулы I _v , который меняется в зависимости от колебательного квантового числа v .

$B_{v}={h \over {8\pi ^{2}cI_{v}}};\quad I_{v}={\frac {m_{A}m_{B}}{m_{A}+m_{B}}}d_{v}^{2}$

где m _A и m _B — массы атомов A и B, а d — расстояние между атомами. Значения термов ротационно-колебательных состояний находятся (в приближении Борна-Оппенгеймера ) путем объединения выражений для вибрации и вращения.

$G(v)+F_{v}(J)=\left[\omega _{e}\left(v+{1 \over 2}\right)+B_{v}J(J+1)\right]-\left[\omega _{e}\chi _{e}\left(v+{1 \over 2}\right)^{2}+DJ^{2}(J+1)^{2}\right]$

Первые два слагаемых в этом выражении соответствуют гармоническому генератору и жесткому ротору, вторая пара слагаемых вносит поправку на ангармонизм и центробежные искажения. Более общее выражение дал Данэм .

Правило отбора для электрических дипольно-разрешенных колебательно-колебательных переходов в случае диамагнитной двухатомной молекулы имеет вид

$\Delta v=\pm 1\ (\pm 2,\pm 3,{\textit {etc.}}$$),\Delta J=\pm 1$

Переход с Δv=±1 известен как фундаментальный переход. Правило выбора имеет два следствия.

1. И колебательные, и вращательные квантовые числа должны измениться. Переход: $\Delta v=\pm 1,\Delta J=0$ (Q-ветвь) запрещена
2. Изменение энергии вращения можно либо вычесть, либо добавить к изменению энергии вибрации, давая P- и R-ветви спектра соответственно.

Расчет волновых чисел перехода более сложен, чем для чистого вращения, поскольку постоянная вращения B _ν различна в основном и возбужденном колебательных состояниях. Упрощенное выражение для волновых чисел получается, если константы центробежных искажений $D^{\prime }$ и $D^{\prime \prime }$ примерно равны между собой.

${\bar {\nu }}=\omega _{0}+(B^{\prime }+B^{\prime \prime })m+(B^{\prime }-B^{\prime \prime })m^{2}-2(D^{\prime }+D^{\prime \prime })m^{3},\quad \omega _{0}=\omega _{e}(1-2\chi _{e})\quad m=\pm 1,\pm 2\ etc.$

Спектр R-ветви оксида азота NO, смоделированный с помощью Spectralcalc, показывающий λ-удвоение, вызванное наличием неспаренного электрона в молекуле

где положительные значения m относятся к R-ветви, а отрицательные значения относятся к P-ветви. Член ω ₀ дает положение (недостающей) Q-ветви, член $(B^{\prime }+B^{\prime \prime })m$ подразумевает последовательность равноотстоящих друг от друга линий в P- и R-ветвях, но третий член, $(B^{\prime }-B^{\prime \prime })m^{2}$показывает, что расстояние между соседними линиями меняется с изменением вращательного квантового числа. Когда $B^{\prime \prime }$ больше, чем $B^{\prime }$, как это обычно бывает, с увеличением J расстояние между линиями уменьшается в R-ветви и увеличивается в P-ветви. Анализ данных инфракрасного спектра окиси углерода дает значение $B^{\prime \prime }$ 1,915 см ⁻¹ и $B^{\prime }$ 1,898 см ⁻¹ . Длины связей легко получаются из этих констант: r ₀ = 113,3 пм, r ₁ = 113,6 пм. Эти длины связей немного отличаются от равновесной длины связи. Это связано с тем, что в основном колебательном состоянии существует нулевая энергия , тогда как равновесная длина связи находится на минимуме на кривой потенциальной энергии. Связь между вращательными постоянными определяется выражением

$B_{v}=B_{eq}-\alpha \left(v+{1 \over 2}\right)$

где ν — колебательное квантовое число, а α — константа вибрационно-вращательного взаимодействия, которую можно рассчитать, если можно найти значения B для двух разных колебательных состояний. Для окиси углерода r _экв = 113,0 ч.

Оксид азота NO представляет собой особый случай, поскольку молекула парамагнитна и имеет один неспаренный электрон. Связь спинового момента электрона с молекулярными колебаниями вызывает лямбда-удвоение. с рассчитанными частотами гармоник 1904,03 и 1903,68 см. ⁻¹ . Уровни вращения также разделены.

Гомоядерные двухатомные молекулы

Квантовая механика гомоядерных двухатомных молекул, таких как диазот N ₂ и фтор F ₂ , качественно такая же, как и для гетероядерных двухатомных молекул, но правила отбора, управляющие переходами, другие. Поскольку электрический дипольный момент гомоядерных двухатомных атомов равен нулю, фундаментальный колебательный переход запрещен электрическим диполем, и молекулы неактивны в инфракрасном диапазоне. Однако слабый квадрупольно-разрешенный спектр N ₂ можно наблюдать при использовании больших пробегов как в лаборатории, так и в атмосфере. Спектры этих молекул можно наблюдать с помощью рамановской спектроскопии, поскольку молекулярные колебания разрешены рамановским рассеянием.

Дикислород представляет собой особый случай, поскольку молекула парамагнитна , поэтому разрешенные магнитным диполем переходы можно наблюдать в инфракрасном диапазоне. Единичный спин электрона имеет три пространственные ориентации относительно вектора вращательного момента молекулы N: так что каждый вращательный уровень разделен на три состояния с полным угловым моментом (вращение молекулы плюс спин электрона) $\mathrm {J\hbar } \,$, J = N + 1, N и N - 1, каждое J-состояние этого так называемого триплета p-типа возникает из-за различной ориентации спина относительно вращательного движения молекулы. Правила отбора магнитно-дипольных переходов допускают переходы между последовательными членами триплета (ΔJ = ±1) так, что для каждого значения квантового числа вращательного углового момента N существует два разрешенных перехода. ¹⁶ Ядро O имеет нулевой угловой момент ядерного спина, поэтому соображения симметрии требуют, чтобы N могло иметь только нечетные значения.

Спектры комбинационного рассеяния двухатомных молекул

Правило выбора такое

$\Delta J=0,\pm 2$

так что спектр имеет O-ветвь (∆ J = −2), Q-ветвь (∆ J = 0) и S-ветвь (∆ J =+2). В приближении B " = B ′ = B волновые числа имеют вид

${\bar {\nu }}(S(J))=\omega _{0}+4BJ+6B=\omega _{0}+6B,\quad \omega _{0}+10B,\quad \omega _{0}+14B,\quad ...$

${\bar {\nu }}(O(J))=\omega _{0}-4BJ+2B=\omega _{0}-6B,\quad \omega _{0}-10B,\quad \omega _{0}-14B,\quad ...$

поскольку S-ветвь начинается с J=0, а O-ветвь с J=2. Итак, в первом приближении расстояние между S (0) и O (2) составляет 12 B а расстояние между соседними линиями как в O-, так и в S-ветвях - 4 B. , Наиболее очевидным эффектом того факта, что B " ≠ B ' является то, что Q-ветвь имеет ряд близко расположенных боковых линий на низкочастотной стороне из-за переходов, в которых Δ J =0 для J =1,2 и т. д. . Полезные разностные формулы, в которых не учитываются центробежные искажения, следующие.

$\Delta _{4}^{\prime \prime }F(J)={\bar {\nu }}[S(J-2)]-{\bar {\nu }}[O(J+2)]=4B^{\prime \prime }(2J+1)$

$\Delta _{4}^{\prime }F(J)={\bar {\nu }}[S(J)]-{\bar {\nu }}[O(J)]=4B^{\prime }(2J+1)$

Молекулярный кислород представляет собой особый случай, поскольку молекула парамагнитна и имеет два неспаренных электрона.

Для гомоядерных двухатомных атомов статистические веса спина ядра приводят к чередованию интенсивностей линий между четными и четными. $J^{\prime \prime }$ и странно- $J^{\prime \prime }$ уровни. Для ядерного спина I = 1/2, как в ¹ Н ₂ и ¹⁹ F ₂ чередование интенсивности 1:3. Для ² Н ₂ и ¹⁴ N ₂ , I =1, а статистические веса равны 6 и 3, так что четные $J^{\prime \prime }$ уровни в два раза интенсивнее. Для ¹⁶ O ₂ ( I =0) все переходы с четными значениями $J^{\prime \prime }$ запрещены.

Многоатомные линейные молекулы

Спектр изгибной моды в 14 Н 14 Н 16 O смоделировано с помощью Spectralcalc. Слабый наложенный спектр обусловлен видами, содержащими 15 N при естественном содержании 0,3%

Спектр перпендикулярной полосы ацетилена C 2 H 2 , смоделированный с помощью Spectralcalc показывая 1,3-чередование интенсивности как в P-, так и в R-ветвях. См. также Холлас, стр. 157.

Спектр асимметричной валентной (параллельной) полосы углекислого газа , 12 С 16 O 2 смоделировано с помощью Spectralcalc. Слабый наложенный спектр обусловлен поглощением первого колебательно-возбужденного уровня (0 1 1 0), который из-за своей малой энергии заселяется при комнатной температуре

Эти молекулы делятся на два класса в соответствии с симметрией : центросимметричные молекулы с точечной группой D _∞h , такие как диоксид углерода , CO ₂ , и этин или ацетилен, HCCH; и нецентросимметричные молекулы с точечной группой C _∞v, такие как цианид водорода HCN и закись азота NNO. Центросимметричные линейные молекулы имеют нулевой дипольный момент , поэтому не демонстрируют чистого спектра вращения в инфракрасной или микроволновой областях. С другой стороны, в некоторых колебательно-возбужденных состояниях молекулы действительно обладают дипольным моментом, поэтому в инфракрасном диапазоне можно наблюдать вращательно-колебательный спектр.

Спектры этих молекул классифицируются по направлению вектора изменения дипольного момента. Когда вибрация вызывает изменение дипольного момента, направленного вдоль оси молекулы термин «параллель» с символом , применяется $\parallel$. Когда вибрация вызывает дипольный момент, направленный перпендикулярно оси молекулы, термин «перпендикуляр» с обозначением применяется $\perp$. В обоих случаях волновые числа P- и R-ветвей следуют той же тенденции, что и в двухатомных молекулах. Эти два класса различаются правилами отбора, применимыми к ротационно-колебательным переходам. Для параллельных переходов правило отбора такое же, как и для двухатомных молекул, а именно, запрещается переход, соответствующий Q-ветви. Примером может служить режим растяжения CH цианида водорода.

переход ΔJ = При перпендикулярном колебании допускается 0. Это означает, что переход разрешен для молекулы с одинаковым вращательным квантовым числом в основном и возбужденном колебательном состоянии для всех заселенных вращательных состояний. Это создает интенсивную, относительно широкую Q-ветвь, состоящую из перекрывающихся линий, обусловленных каждым состоянием вращения. Режим изгиба NNO закиси азота при ок. 590 см ⁻¹ это пример.

Спектры центросимметричных молекул демонстрируют чередующуюся интенсивность линий из-за эффектов симметрии квантового состояния, поскольку поворот молекулы на 180 ° вокруг оси вращения 2-го порядка эквивалентен обмену идентичными ядрами. В углекислом газе атомы кислорода преобладающих изотопных разновидностей ¹² С ¹⁶ O ₂ имеют нулевой спин и являются бозонами , так что полная волновая функция должна быть симметричной, когда два ¹⁶ Ядра О обмениваются. Фактор ядерного спина всегда симметричен для двух ядер с нулевым спином, так что вращательный фактор также должен быть симметричным, что верно только для уровней с четным J. Вращательные уровни с нечетным J существовать не могут, а разрешенные колебательные полосы состоят только из линий поглощения начальных уровней с четным J. Расстояние между соседними линиями в ветвях P и R близко к 4B, а не к 2B, поскольку альтернативные линии отсутствуют. Для ацетилена водороды ¹ ЧАС ¹² С ¹² С ¹ H имеют спин 1/2 и являются фермионами , поэтому полная волновая функция антисимметрична, когда два ¹ Ядра H обмениваются. Как и в случае орто- и параводорода, функция ядерного спина двух атомов водорода имеет три симметричных орто-состояния и одно антисимметричное пара-состояние. Для трех орто-состояний вращательная волновая функция должна быть антисимметричной, соответствующей нечетному J, а для одного пара-состояния она симметрична, соответствуя четному J. Таким образом, популяция нечетных уровней J в три раза превышает популяцию четных уровней J. и чередующиеся интенсивности линий находятся в соотношении 3:1.

Молекулы со сферической вершиной

Вверху: инфракрасный спектр низкого разрешения асимметричной валентной полосы метана (СН ₄ ); нижний: ПГОФЕР смоделированный линейный спектр, игнорируя связь Кориолиса

Эти молекулы имеют равные моменты инерции относительно любой оси и принадлежат точечным группам T _d (тетраэдрический AX ₄ ) и _Oh (октаэдрический AX ₆ ). Молекулы с такой симметрией имеют нулевой дипольный момент, поэтому не имеют чистого спектра вращения в инфракрасной или микроволновой областях.

Тетраэдрические молекулы, такие как метан , CH ₄ , обладают инфракрасно-активными валентными и изгибными колебаниями, принадлежащими к представлению T ₂ (иногда обозначаемому как F ₂ ). Эти колебания трижды вырождены, а вращательные уровни энергии имеют три компонента, разделенные взаимодействием Кориолиса . Значения вращательного члена в первом приближении определяются выражением

$F^{+}=B_{\nu }J(J+1)+2B_{\nu }\zeta _{r}(J+1)$

$F^{0}=B_{\nu }J(J+1)$

$F^{-}=B_{\nu }J(J+1)-2B_{\nu }\zeta _{r}J$

где $\zeta _{r}$ является константой связи Кориолиса. Правило выбора фундаментальной вибрации таково:

$\Delta J=0,\pm 1$

Таким образом, спектр очень похож на спектр перпендикулярного колебания линейной молекулы с сильной Q-ветвью, состоящей из множества переходов, в которых вращательное квантовое число одинаково в основном и возбужденном колебательном состояниях. $J^{\prime }=J^{\prime \prime }=1,2...$ Эффект кориолисовой связи хорошо виден в валентных колебаниях метана CH, хотя детальное исследование показало, что приведенная выше формула первого порядка для кориолисовой связи не подходит для метана.

Симметричные верхние молекулы

Эти молекулы имеют уникальную главную ось вращения порядка 3 или выше. Есть два различных момента инерции и, следовательно, две постоянные вращения. При вращении вокруг любой оси, перпендикулярной единственной оси, момент инерции равен $I_{\perp }$ а постоянная вращения равна $B={h \over {8\pi ^{2}cI_{\perp }}}$, что и для линейных молекул. Однако при вращении вокруг единственной оси момент инерции равен $I_{\parallel }$ а постоянная вращения равна $A={h \over {8\pi ^{2}cI_{\parallel }}}$. Примеры включают аммиак , NH ₃ и метилхлорид , CH ₃ Cl (оба имеют молекулярную симметрию, описываемую точечной группой C _3v ), трифторид бора , BF ₃ и пентахлорид фосфора , PCl ₅ (оба из точечной группы D _3h ), и бензол , C ₆ H ₆ (точечная группа D _6h ).

Для симметричных роторов квантовое число J связано с полным угловым моментом молекулы. Для данного значения J имеет место 2 J +1-кратное вырождение с квантовым числом, при этом M принимает значения + J ...0 ... - J . Третье квантовое число K связано с вращением вокруг главной оси вращения молекулы. Как и в случае с линейными молекулами, переходы классифицируются как параллельные . $\parallel$ или перпендикулярно , $\perp$, в данном случае по направлению изменения дипольного момента относительно главной оси вращения. Третья категория включает в себя определенные обертоны и комбинированные полосы, которые обладают свойствами как параллельных, так и перпендикулярных переходов. Правила выбора такие

$\parallel$ Если K ≠ 0, то Δ J = 0, ±1 и Δ K = 0.

Если K = 0, то ∆ J = ±1 и ∆ K = 0.

$\perp$ Δ J = 0, ±1 и Δ K = ±1

Тот факт, что правила отбора различны, является основанием для классификации и означает, что спектры имеют различный внешний вид, который часто можно сразу распознать.Выражение для рассчитанных волновых чисел P- и R-ветвей можно представить как

${\bar {\nu }}={\bar {\nu }}_{0}+(B^{\prime }+B^{\prime \prime })m+(B^{\prime }-B^{\prime \prime }-D_{J}^{\prime }+D_{J}^{\prime \prime })m^{2}$

$-2(D_{J}^{\prime }+D_{J}^{\prime \prime })m^{3}-(D_{J}^{\prime }-D_{J}^{\prime \prime })m^{4}$

$+\left\{\left[(A^{\prime }-B^{\prime })-(A^{\prime \prime }-B^{\prime \prime })\right]-\left[D_{JK}^{\prime }+D_{JK}^{\prime \prime }\right]m-\left[D_{JK}^{\prime }-D_{JK}^{\prime \prime }\right]m^{2}\right\}K^{2}-(D_{K}^{\prime }-D_{K}^{\prime \prime })K^{4}$

в котором m = J +1 для R-ветви и -J для P-ветви. Три константы центробежного искажения $D_{J},D_{JK}$, и $D_{K}$ необходимы для соответствия значениям терминов каждого уровня. Волновые числа субструктуры, соответствующей каждой полосе, определяются выражением

${\bar {\nu }}={\bar {\nu }}_{sub}+(B^{\prime }-B^{\prime \prime })J(J+1)-(D_{J}^{\prime }-D_{J}^{\prime \prime })J^{2}(J+1)^{2}-(D_{JK}^{\prime }-D_{JK}^{\prime \prime })J(J+1)K^{2}$

${\bar {\nu }}_{sub}$ представляет собой Q-ветвь подструктуры, положение которой определяется выражением

${\bar {\nu }}_{sub}={\bar {\nu }}_{0}+\left[(A^{\prime }-B^{\prime })-(A^{\prime \prime }-B^{\prime \prime })\right]K^{2}-(D_{K}^{\prime }-D_{K}^{\prime \prime })K^{4}$.

Спектр валентной полосы C-Cl в CH 3 Cl (параллельная полоса), смоделированный с помощью Spectralcalc.

Часть спектра асимметричного деформационного колебания ГХГ в CH 3 Cl (перпендикулярная полоса), смоделированная с помощью Spectralcalc

Параллельные полосы

Валентное колебание C-Cl метилхлорида CH ₃ Cl дает параллельную полосу, поскольку изменение дипольного момента совпадает с 3-кратной осью вращения. Линейчатый спектр довольно четко показывает субструктуру этой полосы; на самом деле для полного разрешения тонкой структуры потребуется спектроскопия очень высокого разрешения. Аллен и Кросс показывают части спектра CH ₃ D и дают подробное описание численного анализа экспериментальных данных.

Перпендикулярные полосы

Правило отбора для перпендикулярных полос приводит к большему количеству переходов, чем для параллельных полос. Полосу можно рассматривать как серию подструктур, каждая из которых имеет ветви P, Q и R. Q-ветви разделены примерно 2( A ′- B ′). Типично асимметричное деформационное колебание ГХГ метилхлорида. На нем виден ряд интенсивных Q-ветвей со слабой вращательной тонкой структурой. Анализ спектров усложняется тем фактом, что вибрация в основном состоянии по симметрии считается вырожденной вибрацией, а это означает, что связь Кориолиса также влияет на спектр.

Гибридные группы

Обертоны вырожденной фундаментальной вибрации имеют компоненты более чем одного типа симметрии. Например, первый обертон вибрации, принадлежащей представлению E в такой молекуле, как аммиак, NH ₃ , будет иметь компоненты, принадлежащие A ₁ и E. представлениям Переход к компоненте А ₁ даст параллельную полосу, а переход к компоненте Е — перпендикулярные полосы; в результате получается гибридная группа.

Инверсия в аммиаке

Спектр центральной области симметричного изгибного колебания в аммиаке, смоделированный с помощью Spectralcalc, иллюстрирующая инверсию удвоения.

Инверсия азота в аммиаке

Для аммиака NH ₃ симметричное деформационное колебание наблюдается в виде двух ветвей вблизи 930 см. ⁻¹ и 965 см ⁻¹ . Это так называемое инверсионное удвоение возникает потому, что симметричное деформационное колебание на самом деле представляет собой движение с большой амплитудой, известное как инверсия , при котором атом азота проходит через плоскость трех атомов водорода, подобно инверсии зонтика. Кривая потенциальной энергии такой вибрации имеет двойной минимум для двух пирамидальных геометрий, так что уровни колебательной энергии встречаются парами, которые соответствуют комбинациям колебательных состояний в двух потенциальных минимумах. Два состояния v = 1 объединяются, образуя симметричное состояние (1 ⁺ ) на высоте 932,5 см ⁻¹ над землей (0 ⁺ ) состояние и антисимметричное состояние (1 ⁻ ) на высоте 968,3 см ⁻¹ .

Колебательное основное состояние (v = 0) также удваивается, хотя разница в энергии гораздо меньше, и переход между двумя уровнями можно измерить непосредственно в микроволновой области при температуре ок. 24 ГГц (0,8 см ⁻¹ ). Этот переход имеет историческое значение и использовался в аммиачном мазере , предшественнике лазера .

Асимметричные верхние молекулы

Спектр поглощения ( коэффициент затухания в зависимости от длины волны) жидкой воды (красный) атмосферный водяной пар (зеленый) и лед (синяя линия) между 667 нм и 200 мкм. График для пара представляет собой преобразование данных Синтетический спектр газовой смеси «Чистая H ₂ O» (296 К, 1 атм), полученных из Hitran в информационной веб-системе.

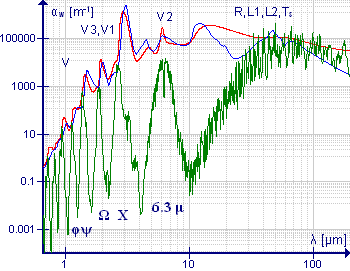
Асимметричные верхние молекулы имеют не более одной или нескольких осей вращения второго порядка. имеются три неравных момента инерции Вокруг трех взаимно перпендикулярных главных осей . Спектры очень сложны. Волновые числа перехода не могут быть выражены аналитической формулой, но могут быть рассчитаны численными методами.

Молекула воды является важным примером молекул этого класса, особенно из-за присутствия водяного пара в атмосфере. Спектр низкого разрешения, показанный зеленым, иллюстрирует сложность спектра. На длинах волн более 10 мкм (или волновых числах менее 1000 см-1) ⁻¹ ) поглощение происходит за счет чистого вращения. Полоса около 6,3 мкм (1590 см ⁻¹ ) обусловлено изгибными колебаниями HOH; значительная ширина этой полосы обусловлена ​​наличием обширной вращательной тонкой структуры. Спектры этой полосы с высоким разрешением показаны у Аллена и Кросса, стр. 221. Симметричные и асимметричные валентные колебания близки друг к другу, поэтому вращательные тонкие структуры этих полос перекрываются. Полосы с более короткими длинами волн представляют собой обертоны и комбинированные полосы, все из которых имеют тонкую вращательную структуру. Спектры среднего разрешения полос около 1600 см-1. ⁻¹ и 3700 см ⁻¹ показаны в Banwell and McCash, стр. 91.

Ро-колебательные полосы молекул асимметричного волчка классифицируются как А-, В- или С-типы для переходов, при которых изменение дипольного момента происходит вдоль оси наименьшего момента инерции к наибольшему.

Экспериментальные методы

Ро-колебательные спектры обычно измеряются с высоким спектральным разрешением . Раньше это достигалось за счет использования решетки Эшелле в качестве элемента спектральной дисперсии в решеточном спектрометре . Это тип дифракционной решетки, оптимизированный для использования более высоких порядков дифракции. Сегодня при всех разрешениях предпочтительным методом является FTIR . Основная причина этого заключается в том, что инфракрасные детекторы по своей природе шумны, а FTIR обнаруживает суммированные сигналы на нескольких длинах волн, одновременно достигая более высокого отношения отношения к шуму благодаря преимуществу Феллгетта в отношении мультиплексированных методов. Разрешающая способность FTIR- спектрометра зависит от максимального замедления движущегося зеркала. Например, для достижения разрешения 0,1 см ⁻¹ , движущееся зеркало должно иметь максимальное смещение на 10 см от своего положения при нулевой разности хода. Конн измерил вибровращательный спектр венерианского CO ₂ при этом разрешении. Спектрометр с 0,001 см ⁻¹ Разрешение теперь доступно коммерчески. Преимущество FTIR в пропускной способности важно для спектроскопии высокого разрешения, поскольку монохроматор в дисперсионном приборе с таким же разрешением будет иметь очень узкие входную и выходную щели .

При измерении спектров газов относительно легко получить очень большие длины оптического пути, используя ячейку многократного отражения. Это важно, поскольку позволяет снизить давление, чтобы минимизировать уширение спектральных линий под давлением, которое может ухудшить разрешение. В продаже имеются пути длиной до 20 м.

Приложение

Метод комбинационных разностей использует различия волновых чисел в P- и R-ветвях для получения данных, которые зависят только от вращательных постоянных в основном колебательном или возбужденном состоянии. Для возбужденного состояния

$\Delta _{2}^{\prime }F(J)^{observed}={\bar {\nu }}[R(J)]-{\bar {\nu }}[P(J)]$

Эту функцию можно подобрать, используя метод наименьших квадратов для данных по угарному газу Харриса и Бертолуччи. Данные рассчитаны по формуле

$\Delta _{2}^{\prime }F(J)^{calculated}=2B^{\prime \prime }\left(2J+1\right)$

в которых центробежное искажение не учитывается, показаны в столбцах, отмеченных цифрой (1). Эта формула подразумевает, что данные должны лежать на прямой линии с наклоном 2B'' и нулевым пересечением. На первый взгляд данные соответствуют этой модели со среднеквадратичным остатком 0,21 см. ⁻¹ . Однако если учесть центробежное искажение, используя формулу

$\Delta _{2}^{\prime }F(J)^{calculated}=(2B^{\prime \prime }-3D^{\prime \prime })\left(2J+1\right)-D^{\prime \prime }\left(2J+1\right)^{3}$

аппроксимация по методу наименьших квадратов заметно улучшена: остаток мс уменьшился до 0,000086 см. ⁻¹ . Рассчитанные данные показаны в столбцах, отмеченных (2).

График разностей R(J)-P(J) в зависимости от 2J+1, взятый из наблюдаемых данных для фундаментального колебания монооксида углерода.

Волновые числа/см ⁻¹ для основной вращательно-колебательной полосы монооксида углерода

Дж	2Дж+1	$\Delta _{2}^{\prime }F(J)$	Рассчитано (1)	Остаток (1)	Рассчитано (2)	Остаток (2)
1	3	11.4298	11.3877	0.0421	11.4298	−0.000040
2	5	19.0493	18.9795	0.0698	19.0492	0.000055
3	7	26.6680	26.5713	0.0967	26.6679	0.000083
4	9	34.2856	34.1631	0.1225	34.2856	0.000037
5	11	41.9020	41.7549	0.1471	41.9019	0.000111
6	13	49.5167	49.3467	0.1700	49.5166	0.000097
7	15	57.1295	56.9385	0.1910	57.1294	0.000089
8	17	64.7401	64.5303	0.2098	64.7400	0.000081
9	19	72.3482	72.1221	0.2261	72.3481	0.000064
10	21	79.9536	79.7139	0.2397	79.9535	0.000133
11	23	87.5558	87.3057	0.2501	87.5557	0.000080
12	25	95.1547	94.8975	0.2572	95.1546	0.000100
13	27	102.7498	102.4893	0.2605	102.7498	−0.000016
14	29	110.3411	110.0811	0.2600	110.3411	0.000026
15	31	117.9280	117.6729	0.2551	117.9281	−0.000080
16	33	125.5105	125.2647	0.2458	125.5105	−0.000041
17	35	133.0882	132.8565	0.2317	133.0882	0.000035
18	37	140.6607	140.4483	0.2124	140.6607	0.000043
19	39	148.2277	148.0401	0.1876	148.2277	−0.000026
20	41	155.7890	155.6319	0.1571	155.7891	−0.000077
21	43	163.3443	163.2237	0.1206	163.3444	−0.000117
22	45	170.8934	170.8155	0.0779	170.8935	−0.000053
23	47	178.4358	178.4073	0.0285	178.4359	−0.000093
24	49	185.9713	185.9991	−0.0278	185.9714	−0.000142
25	51	193.4997	193.5909	−0.0912	193.4998	−0.000107
26	53	201.0206	201.1827	−0.1621	201.0207	−0.000097
27	55	208.5338	208.7745	−0.2407	208.5338	−0.000016
28	57	216.0389	216.3663	−0.3274	216.0389	0.000028
20	59	223.5357	223.9581	−0.4224	223.5356	0.000128
30	61	231.0238	231.5499	−0.5261	231.0236	0.000178

Библиография

• Аллен, ХК; Кросс, ПК (1963). Молекулярные виброторы; теория и интерпретация инфракрасных спектров высокого разрешения . Нью-Йорк: Уайли.
• Аткинс, П.В.; де Паула, Дж. (2006). Физическая химия (8-е изд.). Издательство Оксфордского университета. стр. 431–469 . ISBN  0198700725 . Глава (Молекулярная спектроскопия), раздел (Вращательные спектры) и номера страниц могут отличаться в разных изданиях.
• Банвелл, Колин Н.; Маккэш, Элейн М. (1994). Основы молекулярной спектроскопии (4-е изд.). МакГроу-Хилл. п. 40 . ISBN  0-07-707976-0 .
• Холлас, MJ (1996). Современная спектроскопия (3-е изд.). Уайли. ISBN  0471965227 .
• Строган, BP; Уокер, С. (1976). Спектроскопия . Том. 2 (3-е изд.). Чепмен и Холл. стр. 176–204. ISBN  0-470-15032-7 .

Внешние ссылки

• Имитатор инфракрасных газовых спектров
• База данных двухатомных спектров NIST
• База данных триатомных спектров NIST
• База данных спектров углеводородов NIST