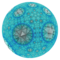
Додекаэдрические соты порядка 6
| Додекаэдрические соты порядка 6 | |
|---|---|
 Перспективная проекция в рамках модели диска Пуанкаре | |
| Тип | Гиперболические обычные соты Паракомпактный однородный сотовый |
| Символ Шлефли | {5,3,6} {5,3 [3] } |
| Диаграмма Кокстера | |
| Клетки | {5,3} |
| Лица | пятиугольник {5} |
| Краевая фигура | шестигранник {6} |
| Вершинная фигура |   треугольная плитка |
| Двойной | Шестиугольная плитка Орден-5 сотовая |
| Группа Коксетера | , [5,3,6] , [5,3 [3] ] |
| Характеристики | Регулярный, квазирегулярный |
— Додекаэдрические соты 6-го порядка одна из 11 паракомпактных правильных сот в гиперболическом трёхмерном пространстве . Он паракомпактный , поскольку имеет фигуры вершин, состоящие из бесконечного числа граней, причем все вершины представляют собой идеальные точки, находящиеся на бесконечности. Он имеет символ Шлефли {5,3,6} с шестью идеальными додекаэдрическими ячейками, окружающими каждый край сот. Каждая вершина идеальна и окружена бесконечным множеством додекаэдров. Соты имеют треугольную фигуру вершин .
Геометрические соты — это заполнение пространства многогранными ячейками более высокой размерности или ячейками , чтобы не было пробелов. Это пример более общего математического разбиения или мозаики в любом количестве измерений.
Соты обычно строятся в обычном евклидовом («плоском») пространстве, как и выпуклые однородные соты . Они также могут быть построены в неевклидовых пространствах , таких как гиперболические однородные соты . Любой конечный однородный многогранник можно спроецировать на его описанную сферу, чтобы сформировать однородную соту в сферическом пространстве.
Симметрия
[ редактировать ]Конструкция полусимметрии существует как ![]()
![]()
![]()
![]()
![]() с попеременно окрашенными додекаэдрическими клетками.
с попеременно окрашенными додекаэдрическими клетками.
Изображения
[ редактировать ] Модель центрирована по ячейкам внутри модели диска Пуанкаре , при этом точка обзора затем помещается в начало координат. |
Додекаэдрические соты 6-го порядка аналогичны двумерной гиперболической пятиугольной мозаике бесконечного порядка , {5,∞}, с пятиугольными гранями и вершинами на идеальной поверхности.
Связанные многогранники и соты
[ редактировать ]Додекаэдрические соты 6-го порядка представляют собой правильные гиперболические соты в трехмерном пространстве и одни из 11 паракомпактных.
| 11 паракомпактных стандартных сот | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 {6,3,3} |
 {6,3,4} |
 {6,3,5} |
 {6,3,6} |
 {4,4,3} |
 {4,4,4} | ||||||
 {3,3,6} |
 {4,3,6} |
 {5,3,6} |
 {3,6,3} |
 {3,4,4} | |||||||
имеется 15 однородных сот [5,3,6] В семействе групп Кокстера , включая эту правильную форму и ее правильную двойственную форму, шестиугольную мозаику пятого порядка .
Додекаэдрические соты 6-го порядка являются частью последовательности правильных полихор и сот с треугольными фигурами вершин мозаики :
| Форма | Паракомпакт | Некомпактный | |||||
|---|---|---|---|---|---|---|---|
| Имя | {3,3,6} | {4,3,6} | {5,3,6} | {6,3,6} | {7,3,6} | {8,3,6} | ... {∞,3,6} |
| Изображение | 
|

|

|

|

|

|

|
| Клетки | {3,3} |
{4,3} |
{5,3} |
{6,3} |
{7,3} |
{8,3} |
{∞,3} |
Он также является частью последовательности правильных многогранников и сот с додекаэдрическими ячейками:
| {5,3,p} многогранники |
|---|
Выпрямленные додекаэдрические соты порядка 6
[ редактировать ]| Выпрямленные додекаэдрические соты порядка 6 | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символы Шлефли | г {5,3,6} т 1 {5,3,6} |
| Диаграммы Кокстера | |
| Клетки | г{5,3} {3,6} |
| Лица | треугольник {3} пятиугольник {5} |
| Вершинная фигура | 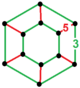 шестиугольная призма |
| Группы Кокстера | , [5,3,6] , [5,3 [3] ] |
| Характеристики | Вершинно-транзитивный, реберно-транзитивный |
Выпрямленные додекаэдрические соты 6-го порядка , t 1 {5,3,6}, имеют икосододекаэдр и треугольные ячейки мозаики, соединенные в шестиугольной призмы вершинную фигуру .
Он похож на двумерную гиперболическую пентаапейрогональную мозаику r{5,∞} с пятиугольными и апейрогональными гранями.
| Космос | ЧАС 3 | ||||||
|---|---|---|---|---|---|---|---|
| Форма | Паракомпакт | Некомпактный | |||||
| Имя | г {3,3,6} |
г {4,3,6} |
г {5,3,6} |
г {6,3,6} |
г {7,3,6} |
... г{∞,3,6} | |
| Изображение | 
|

|

|

|
|||
| Клетки {3,6} |
г{3,3} |
г{4,3} |
г{5,3} |
г{6,3} |
г{7,3} |
г{∞,3} | |
Усеченные додекаэдрические соты порядка 6
[ редактировать ]| Усеченные додекаэдрические соты порядка 6 | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символы Шлефли | т{5,3,6} т 0,1 {5,3,6} |
| Диаграммы Кокстера | |
| Клетки | т{5,3} {3,6} |
| Лица | треугольник {3} десятиугольник {10} |
| Вершинная фигура | 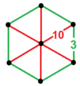 шестиугольная пирамида |
| Группы Кокстера | , [5,3,6] , [5,3 [3] ] |
| Характеристики | Вершинно-транзитивный |
Усеченные додекаэдрические соты 6-го порядка , t 0,1 {5,3,6}, имеют усеченный додекаэдр и треугольные ячейки мозаики, соединенные в шестиугольной пирамиды вершинную фигуру .
Двуусеченные додекаэдрические соты порядка 6
[ редактировать ]Додекаэдрические соты 6-го порядка с усеченными битами аналогичны сотам с гексагональной мозаикой 5-го порядка .
Скошенные додекаэдрические соты порядка 6
[ редактировать ]| Скошенные додекаэдрические соты порядка 6 | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символы Шлефли | рр{5,3,6} т 0,2 {5,3,6} |
| Диаграммы Кокстера | |
| Клетки | рр{5,3} рр{6,3} {}x{6} |
| Лица | треугольник {3} квадрат {4} пятиугольник {5} шестигранник {6} |
| Вершинная фигура |  клин |
| Группы Кокстера | , [5,3,6] , [5,3 [3] ] |
| Характеристики | Вершинно-транзитивный |
Соты со складчатыми додекаэдрами 6-го порядка , t 0,2 {5,3,6}, имеют ромбикосидодекаэдр , тригексагональную мозаику и шестиугольной призмы ячейки с клиновидной вершиной.
Кантиусеченные додекаэдрические соты порядка 6
[ редактировать ]| Кантиусеченные додекаэдрические соты порядка 6 | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символы Шлефли | тр{5,3,6} т 0,1,2 {5,3,6} |
| Диаграммы Кокстера | |
| Клетки | тр{5,3} т{3,6} {}x{6} |
| Лица | квадрат {4} шестигранник {6} десятиугольник {10} |
| Вершинная фигура | 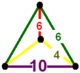 зеркальная клиновидная кость |
| Группы Кокстера | , [5,3,6] , [5,3 [3] ] |
| Характеристики | Вершинно-транзитивный |
Кантиусеченные додекаэдрические соты 6-го порядка , t 0,1,2 {5,3,6}, имеют усеченный икосододекаэдр , шестиугольную мозаику и грани шестиугольной призмы с зеркальной фигурой клиновидной вершины .
Ранцинированные додекаэдрические соты порядка 6
[ редактировать ]Срезанные додекаэдрические соты 6-го порядка аналогичны сеченным сотам с шестиугольной черепицей 5-го порядка .
Додекаэдрические соты Runcitусеченного порядка 6
[ редактировать ]| Додекаэдрические соты Runcitусеченного порядка 6 | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символы Шлефли | т 0,1,3 {5,3,6} |
| Диаграммы Кокстера | |
| Клетки | т{5,3} рр{6,3} {}х{10} {}x{6} |
| Лица | квадрат {4} шестигранник {6} десятиугольник {10} |
| Вершинная фигура | равнобедренно-трапециевидная пирамида |
| Группы Кокстера | , [5,3,6] |
| Характеристики | Вершинно-транзитивный |
Усеченные додекаэдрические соты 6-го порядка , t 0,1,3 {5,3,6}, имеют усеченный додекаэдр , ромбитригексагональную мозаику , десятиугольную призму и грани шестиугольной призмы , с равнобедренно-трапециевидной пирамиды фигурой вершины .
Додекаэдрические соты ранциконтеллярного порядка 6
[ редактировать ]аналогичны Додекаэдрические соты 6-го порядка с ранцикантелляцией сотам с гексагональной черепицей 5-го порядка .
Всеусеченные додекаэдрические соты порядка 6
[ редактировать ]Всеусеченные додекаэдрические соты 6-го порядка аналогичны всеусеченным шестиугольным мозаичным сотам 5-го порядка .
См. также
[ редактировать ]- Выпуклые однородные соты в гиперболическом пространстве
- Регулярные мозаики гиперболического трехмерного пространства
- Паракомпактные однородные соты
Ссылки
[ редактировать ]- Коксетер , Правильные многогранники , 3-е. изд., Dover Publications, 1973. ISBN 0-486-61480-8 . (Таблицы I и II: Правильные многогранники и соты, стр. 294–296)
- Красота геометрии: двенадцать эссе (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (Глава 10, Правильные соты в гиперболическом пространстве ) Таблица III
- Джеффри Р. Уикс. Форма пространства, 2-е издание ISBN 0-8247-0709-5 (Глава 16-17: Геометрии трехмерных многообразий I, II)
- Нормана Джонсона Равномерные многогранники , рукопись
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
- Н. В. Джонсон: Геометрии и преобразования , (2018) Глава 13: Гиперболические группы Кокстера