Треугольная мозаика бесконечного порядка

Треугольная мозаика бесконечного порядка
Модель диска Пуанкаре гиперболической плоскости
Тип	Гиперболическая регулярная мозаика
Конфигурация вершин	3 ^∞
Символ Шлефли	{3,∞}
Символ Витхоффа	∞ \| 3 2
Диаграмма Кокстера
Группа симметрии	[∞,3], (*∞32)
Двойной	Апейрогональная мозаика порядка 3
Характеристики	Вершинно-транзитивный , реберно-транзитивный , грани-транзитивный

В геометрии треугольное замощение бесконечного порядка представляет собой регулярное замощение гиперболической плоскости с символом Шлефли {3, ∞}. Все вершины идеальны , расположены на «бесконечности» и видны на границе проекции гиперболического диска Пуанкаре .

Симметрия

Форма более низкой симметрии имеет чередующиеся цвета и представлена циклическим символом {(3,∞,3)}, . Мозаика также представляет фундаментальные области симметрии *∞∞∞ , которые можно увидеть с помощью трех цветов линий, представляющих три зеркала конструкции.

Чередование цветной плитки	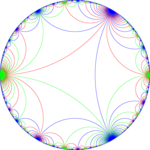*∞∞∞ симметрия	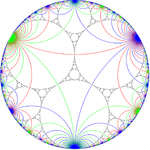Аполлоническая прокладка с симметрией *∞∞∞

Связанные многогранники и мозаика

Это разбиение топологически связано как часть последовательности правильных многогранников с символом Шлефли {3,p}.

* n 32 мутация симметрии правильных мозаик: {3, n } v т и
Spherical				Euclid.	Compact hyper.		Paraco.	Noncompact hyperbolic

3.3	3³	3⁴	3⁵	3⁶	3⁷	3⁸	3^∞	3¹²ⁱ	3⁹ⁱ	3⁶ⁱ	3³ⁱ

Паракомпактные равномерные разбиения семейства [∞,3] v т и
Symmetry: [∞,3], (*∞32)							[∞,3]⁺ (∞32)	[1⁺,∞,3] (*∞33)		[∞,3⁺] (3*∞)

		=	=	=				= or	= or	=

{∞,3}	t{∞,3}	r{∞,3}	t{3,∞}	{3,∞}	rr{∞,3}	tr{∞,3}	sr{∞,3}	h{∞,3}	h₂{∞,3}	s{3,∞}
Uniform duals


V∞³	V3.∞.∞	V(3.∞)²	V6.6.∞	V3^∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V(3.∞)³		V3.3.3.3.3.∞

Паракомпактные гиперболические равномерные мозаики в семействе [(∞,3,3)] v т и
Symmetry: [(∞,3,3)], (*∞33)							[(∞,3,3)]⁺, (∞33)



(∞,∞,3)	t_0,1(∞,3,3)	t₁(∞,3,3)	t_1,2(∞,3,3)	t₂(∞,3,3)	t_0,2(∞,3,3)	t_0,1,2(∞,3,3)	s(∞,3,3)
Dual tilings



V(3.∞)³	V3.∞.3.∞	V(3.∞)³	V3.6.∞.6	V(3.3)^∞	V3.6.∞.6	V6.6.∞	V3.3.3.3.3.∞

Другие треугольные мозаики бесконечного порядка

Нерегулярная треугольная мозаика бесконечного порядка может быть создана рекурсивным процессом из центрального треугольника, как показано здесь:

См. также

Ссылки

Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
«Глава 10: Правильные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе . Дуврские публикации. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .

Внешние ссылки