Симметрия (геометрия)

В геометрии объект обладает симметрией , если существует операция или преобразование (например , перемещение , масштабирование , вращение или отражение ), которое отображает фигуру/объект на самого себя (т. е. объект имеет инвариантность относительно преобразования). [1] Таким образом, симметрию можно рассматривать как иммунитет к изменениям. [2] Например, круг, повернутый вокруг своего центра, будет иметь ту же форму и размер, что и исходный круг, поскольку все точки до и после преобразования будут неразличимы. Таким образом, говорят, что круг симметричен относительно вращения или обладает вращательной симметрией . Если изометрия представляет собой отражение плоской фигуры относительно линии, то говорят, что фигура обладает отражательной симметрией или линейной симметрией ; [3] Также возможно, что фигура/объект будет иметь более одной линии симметрии. [4]
Типы симметрий, возможные для геометрического объекта, зависят от набора доступных геометрических преобразований и от того, какие свойства объекта должны оставаться неизменными после преобразования. Поскольку композиция двух преобразований также является преобразованием, и каждое преобразование по определению имеет обратное преобразование, которое его отменяет, набор преобразований, при которых объект является симметричным, образует математическую группу , группу симметрии объекта. [5]
Евклидовы симметрии в целом
[ редактировать ]Наиболее распространенная группа преобразований, применяемых к объектам, называется евклидовой группой « изометрий », которые представляют собой преобразования, сохраняющие расстояние в пространстве, обычно называемые двумерными или трехмерными (т. е. в плоской геометрии или объемной геометрии евклидовы пространства ). . Эти изометрии состоят из отражений , вращений , перемещений и комбинаций этих основных операций. [6] При изометрическом преобразовании геометрический объект называется симметричным, если после преобразования объект неотличим от объекта до преобразования. [7] Геометрический объект обычно симметричен только относительно подмножества или « подгруппы » всех изометрий. Ниже описаны виды подгрупп изометрии, за которыми следуют другие виды групп преобразований, а также типы инвариантности объектов, возможные в геометрии.
По теореме Картана-Дьедонне ортогональное преобразование в n -мерном пространстве может быть представлено композицией не более чем n отражений.
| 1Д | 2D | 3D | 4D | |||||
| Размышления | Точка | Аффинный | Точка | Аффинный | Точка | Аффинный | Точка | Аффинный |
|---|---|---|---|---|---|---|---|---|
| 1 | Отражение | Отражение | Отражение | Отражение | ||||
| 2 | Перевод | Вращение | Перевод | Вращение | Перевод | Вращение | Перевод | |
| 3 | трансфлексия | Роторное отражение | трансфлексия | Роторное отражение | трансфлексия | |||
| 4 | Ротационный перевод | Двойное вращение | Ротационный перевод | |||||
| 5 | Роторное трансфлексирование | |||||||
Отражательная симметрия
[ редактировать ]Отражательная симметрия, линейная симметрия, зеркальная симметрия, зеркальная симметрия или двусторонняя симметрия - это симметрия относительно отражения. [8]
В одном измерении существует точка симметрии, вокруг которой происходит отражение; в двух измерениях есть ось симметрии (она же линия симметрии), а в трех измерениях — плоскость симметрии. [3] [9] Объект или фигура, у которой каждая точка имеет взаимно однозначное отображение на другую, равноудаленную от общей плоскости и по ее противоположные стороны, называется зеркально-симметричной (подробнее см. Зеркальное изображение ).
Осью симметрии двумерной фигуры называется линия такая, что при построении перпендикуляра любые две точки, лежащие на перпендикуляре на равных расстояниях от оси симметрии, будут одинаковыми. Другой способ подумать об этом состоит в том, что если фигуру сложить пополам по оси, две половины будут идентичны, как зеркальные отражения друг друга. Например. квадрат имеет четыре оси симметрии, потому что есть четыре разных способа сложить его так, чтобы края совпадали друг с другом. Другим примером может служить круг , который по той же причине имеет бесконечное количество осей симметрии, проходящих через его центр. [10]
Если буква Т отражается вдоль вертикальной оси, она выглядит так же. Иногда это называют вертикальной симметрией. Таким образом, можно однозначно описать это явление, сказав, что «T имеет вертикальную ось симметрии» или что «T имеет лево-правую симметрию».
Треугольники коршуны с отражательной симметрией — равнобедренные , четырехугольники с такой симметрией — и равнобедренные трапеции . [11]
Для каждой линии или плоскости отражения группа симметрии изоморфна точечные C s (подробнее см. группы в трех измерениях), одному из трех типов второго порядка ( инволюции ), следовательно, алгебраически изоморфна C 2 . Фундаментальная область — это полуплоскость или полупространство . [12]
Точечное отражение и другие инволютивные изометрии
[ редактировать ]
Симметрию отражения можно обобщить на другие изометрии - мерного m пространства, которые являются инволюциями , например
- ( Икс 1 , ..., Икс м ) ↦ (- Икс 1 , ..., - Икс k , Икс k +1 , ..., Икс м )
в некоторой системе декартовых координат . Это отражает пространство вдоль ( m − k ) -мерного аффинного подпространства . [13] Если k = m , то такое преобразование известно как точечное отражение или инверсия через точку . На плоскости ( m = 2) точечное отражение аналогично повороту на пол- оборота (180°); см. ниже. Антиподальная симметрия — это альтернативное название симметрии точечного отражения через начало координат. [14]
Такое «отражение» сохраняет ориентацию тогда и только тогда, когда k — четное число. [15] Отсюда следует, что при m = 3 (как и при других нечетных m ) точечное отражение меняет ориентацию пространства, подобно зеркальной симметрии. Это объясняет, почему в физике термин P- симметрия (P означает четность ) используется как для точечного отражения, так и для зеркальной симметрии. Поскольку точечное отражение в трех измерениях изменяет левую систему координат на правую , симметрию относительно точечного отражения также называют лево-правой симметрией. [16]
Вращательная симметрия
[ редактировать ]
Вращательная симметрия — это симметрия относительно некоторых или всех вращений в m -мерном евклидовом пространстве. Вращения — это прямые изометрии , то есть изометрии, сохраняющие ориентацию . [17] Следовательно, группа симметрии вращательной симметрии является подгруппой специальной евклидовой группы E + ( м ) .
Симметрия относительно всех вращений вокруг всех точек подразумевает трансляционную симметрию относительно всех перемещений (поскольку перемещения представляют собой композиции вращений вокруг различных точек), [18] а группа симметрии — это целое E + ( м ). Это не применимо к объектам, поскольку делает пространство однородным, но может применяться к физическим законам.
Для симметрии относительно вращения вокруг точки можно взять эту точку за начало координат. Эти вращения образуют специальную ортогональную группу SO( m ), которую можно представить группой m × m ортогональных матриц размера с определителем 1. Для m = 3 это группа вращений SO(3) . [19]
Немного иначе говоря, группа вращения объекта — это группа симметрии внутри E. + ( m ) — группа жестких движений; [20] то есть пересечение полной группы симметрии и группы жестких движений. Для киральных объектов это то же самое, что и полная группа симметрии.
Законы физики SO(3)-инвариантны, если они не различают разные направления в пространстве. Согласно теореме Нётер , вращательная симметрия физической системы эквивалентна углового момента закону сохранения . [21] Дополнительную информацию см. в разделе вращательная инвариантность .
Трансляционная симметрия
[ редактировать ]
Трансляционная симметрия оставляет объект инвариантным относительно дискретной или непрерывной группы переводов. . [22] На иллюстрации справа показаны четыре конгруэнтных следа, созданные в результате перемещения вдоль стрелки. Если бы линия следов простиралась до бесконечности в обоих направлениях, то они имели бы дискретную трансляционную симметрию; любой перевод, который сопоставлял один след с другим, оставил бы всю строку неизменной.
Симметрия отражения скольжения
[ редактировать ]
В 2D симметрия скользящего отражения (также называемая симметрией плоскости скольжения в 3D и трансфлексией в целом) означает, что отражение в линии или плоскости в сочетании с перемещением вдоль линии или в плоскости приводит к созданию одного и того же объекта ( например, в случае со следами). [2] [23] Композиция двух скользящих отражений приводит к трансляционной симметрии с удвоенным вектором трансляции. Группа симметрии, включающая скользящие отражения и связанные с ними трансляции, представляет собой фриза p11g и изоморфна бесконечной циклической группе Z. группу
Роторно-отражательная симметрия
[ редактировать ]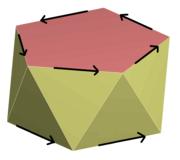
В 3D вращательное отражение , роторное отражение или неправильное вращение — это вращение вокруг оси в сочетании с отражением в плоскости, перпендикулярной этой оси. [24] Группы симметрии, связанные с роторными отражениями, включают:
- если угол поворота не имеет общего делителя с 360°, группа симметрии не дискретна.
- если роторное отражение имеет угол поворота 2 n -кратный (угол 180°/ n ), то группа симметрии S 2 n порядка 2 n (не путать с симметричными группами , для которых используются те же обозначения; аннотация группа — C 2n ). Особым случаем является n = 1, инверсия , поскольку она не зависит от оси и плоскости. Для него характерна именно точка инверсии.
- Группа C nh (угол 360°/ n ); для нечетного n это порождается единственной симметрией, а абстрактная группа — C 2 n для четного n . Это не базовая симметрия, а комбинация.
Дополнительную информацию см. в разделе группы точек в трех измерениях .
Винтовая симметрия
[ редактировать ]В 3D-геометрии и выше винтовая ось (или вращательное перемещение) представляет собой комбинацию вращения и перемещения вдоль оси вращения. [25]
Винтовая симметрия — это вид симметрии, наблюдаемый в повседневных предметах, таких как пружины , Slinky игрушки , сверла и шнеки . Концепцию спиральной симметрии можно представить как трассировку в трехмерном пространстве, возникающую в результате вращения объекта с постоянной угловой скоростью и одновременного перемещения с постоянной линейной скоростью вдоль его оси вращения. В любой момент времени эти два движения объединяются, образуя угол намотки , который помогает определить свойства прослеживаемой спирали. [26] Когда объект отслеживания быстро вращается и медленно перемещается, угол намотки будет близок к 0°. И наоборот, если объект вращается медленно и быстро перемещается, угол намотки приблизится к 90 °.

Можно выделить три основных класса спиральной симметрии, основанные на взаимодействии угла намотки и симметрии перемещения вдоль оси:


- Бесконечная спиральная симметрия : если нет никаких отличительных особенностей по длине спирали или спиралеподобного объекта, объект будет иметь бесконечную симметрию, очень похожую на симметрию круга, но с дополнительным требованием перемещения вдоль длинной оси объекта — чтобы вернуть ему первоначальный вид. [27] Спиралеобразным объектом называется объект, который имеет в каждой точке правильный угол закручивания спирали, но который также может иметь поперечное сечение неопределенно высокой сложности при условии, что существует точно такое же сечение (обычно после вращения) при каждая точка по длине объекта. Простые примеры включают равномерно намотанные пружины, пружины, сверла и шнеки. Точнее говоря, объект имеет бесконечную спиральную симметрию, если при любом небольшом повороте объекта вокруг его центральной оси существует точка поблизости (расстояние перевода) на этой оси, в которой объект будет выглядеть точно так же, как раньше. Именно эта бесконечная спиральная симметрия порождает любопытную иллюзию движения по длине вращающегося шнека или шнека. Это также обеспечивает механически полезную способность таких устройств перемещать материалы по их длине при условии, что они сочетаются с такой силой, как сила тяжести или трение, которая позволяет материалам сопротивляться простому вращению вместе с буром или шнеком.
- n -кратная спиральная симметрия : если требование идентичности всех поперечных сечений спирального объекта ослабляется, тогда становятся возможными дополнительные меньшие спиральные симметрии. Например, поперечное сечение спирального объекта может меняться, но при этом может повторяться регулярным образом вдоль оси спирального объекта. Следовательно, объекты этого типа будут проявлять симметрию после поворота на некоторый фиксированный угол θ и перемещения на некоторое фиксированное расстояние, но, как правило, не будут инвариантными для любого угла поворота. Если угол поворота, при котором возникает симметрия, равномерно делится на полный круг (360 °), то результатом является спиральный эквивалент правильного многоугольника. Этот случай называется n-кратной спиральной симметрией , где n = 360° (например, случай двойной спирали ). Эту концепцию можно далее обобщить, включив в нее случаи, когда кратен 360° , то есть цикл в конечном итоге повторяется, но только после более чем одного полного оборота спирального объекта.
- Неповторяющаяся спиральная симметрия : это тот случай, когда угол поворота θ, необходимый для соблюдения симметрии, иррационален . Угол поворота никогда не повторяется в точности, сколько бы раз ни поворачивалась спираль. Такие симметрии создаются с помощью неповторяющейся группы точек в двух измерениях . ДНК , содержащая примерно 10,5 пар оснований на оборот, является примером такого типа неповторяющейся спиральной симметрии. [28]
Симметрия двойного вращения
[ редактировать ]
В 4D симметрия двойного вращения может быть создана как комбинация двух ортогональных вращений. [29] Это похоже на трехмерную винтовую ось, которая представляет собой сочетание вращения и ортогонального перемещения.
Неизометрические симметрии
[ редактировать ]Более широкое определение геометрической симметрии допускает операции из более крупной группы, чем евклидова группа изометрий. Примеры более крупных групп геометрической симметрии:
- Группа преобразований подобия ; [30] т. е. аффинные преобразования, представленные матрицей A , которая является скаляром, умноженным на ортогональную матрицу . Таким образом гомотетия добавляется , самоподобие считается симметрией.
- Группа аффинных преобразований, представленная матрицей A с определителем 1 или -1; т. е. преобразования, сохраняющие площадь. [31]
- Это добавляет, например, симметрию наклонного отражения .
- Группа всех биективных аффинных преобразований .
- Группа преобразований Мёбиуса , сохраняющих двойные отношения .
- Это добавляет, например, инверсивные отражения, такие как круговое отражение на плоскости.
В программе Феликса Кляйна « Эрланген » каждая возможная группа симметрий определяет геометрию, в которой объекты, связанные членом группы симметрии, считаются эквивалентными. [32] Например, евклидова группа определяет евклидову геометрию , тогда как группа преобразований Мёбиуса определяет проективную геометрию .
Масштабная симметрия и фракталы
[ редактировать ]
Масштабная симметрия означает, что если объект увеличивается или уменьшается в размерах, новый объект имеет те же свойства, что и оригинал. [33] Это самоподобие наблюдается во многих природных структурах, таких как кучевые облака, молнии, папоротники и береговые линии, в широком диапазоне масштабов. Обычно он не встречается в гравитационно-связанных структурах, например, в форме ног слона и мыши ( так называемое аллометрическое масштабирование ). Точно так же, если бы свеча из мягкого воска была увеличена до размеров высокого дерева, она сразу же рухнула бы под собственным весом.
Более тонкую форму масштабной симметрии демонстрируют фракталы . По замыслу Бенуа Мандельброта , фракталы — это математическое понятие, в котором структура сложной формы выглядит одинаково при любой степени увеличения . [34] хорошо видно на множестве Мандельброта . Берег является примером естественного фрактала, поскольку он сохраняет схожую сложность на всех уровнях — от изображения со спутника до микроскопического исследования того, как вода бьется о отдельные песчинки. Еще одним примером является ветвление деревьев, которое позволяет маленьким веточкам заменять полноценные деревья в диорамах .
Поскольку фракталы могут создавать видимость закономерностей в природе , они обладают красотой и узнаваемостью, которые обычно нельзя увидеть в математически созданных функциях. Фракталы также нашли место в компьютерных киноэффектах , где их способность создавать сложные кривые с фрактальной симметрией приводит к созданию более реалистичных виртуальных миров .
Абстрактная симметрия
[ редактировать ]Взгляд Кляйна
[ редактировать ]С каждой геометрией Феликс Кляйн связывал основную группу симметрий . Иерархия геометрий, таким образом, математически представляется как иерархия этих групп и иерархия их инвариантов . Например, длины, углы и площади сохраняются по отношению к евклидовой группе симметрий, тогда как только структура инцидентности и двойное отношение сохраняются при самых общих проективных преобразованиях . Понятие параллелизма , сохраняющееся в аффинной геометрии , не имеет смысла в проективной геометрии . Затем, абстрагируя основные группы симметрий от геометрий, отношения между ними могут быть восстановлены на уровне группы. Поскольку группа аффинной геометрии является подгруппой группы проективной геометрии, любое понятие, инвариантное в проективной геометрии, априори имеет смысл в аффинной геометрии; но не наоборот. Если вы добавите необходимые симметрии, вы получите более мощную теорию, но с меньшим количеством концепций и теорем (которые будут более глубокими и общими).
Взгляд Терстона
[ редактировать ]Уильям Терстон представил аналогичную версию симметрии в геометрии. Модельная геометрия представляет собой односвязное гладкое многообразие X вместе с транзитивным действием группы Ли G на X с компактными стабилизаторами. Группу Ли можно рассматривать как группу симметрий геометрии.
Геометрия модели называется максимальной, если G максимальна среди групп, гладко и транзитивно действующих на X с компактными стабилизаторами, т. е. если она является максимальной группой симметрий. Иногда это условие включается в определение геометрии модели.
Геометрическая структура на многообразии M — это диффеоморфизм M в X /Γ для некоторой модельной геометрии X , где Γ — дискретная подгруппа группы G, действующая на X. свободно Если данное многообразие допускает геометрическую структуру, то оно допускает такую, модель которой является максимальной.
Геометрия трехмерной модели X соответствует гипотезе геометризации, если она максимальна и существует хотя бы одно компактное многообразие с геометрической структурой, смоделированной на X . Терстон классифицировал 8 геометрий моделей, удовлетворяющих этим условиям; они перечислены ниже и иногда называются геометриями Терстона . (Существует также бесчисленное множество геометрий моделей без компактных частных.)
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Мартин, Г. (1996). Геометрия преобразований: введение в симметрию . Спрингер. п. 28.
- ^ Jump up to: а б «Симметрия | Размышления о геометрии | Подземная математика» . Undergroundmathematics.org . Проверено 6 декабря 2019 г.
- ^ Jump up to: а б «Симметрия — MathBitsNotebook (Гео — CCSS Math)» . mathbitsnotebook.com . Проверено 6 декабря 2019 г.
- ^ Фрайтаг, Марк (2013). Математика для учителей начальной школы: процессный подход . Cengage Обучение. п. 721.
- ^ Миллер, Уиллард младший (1972). Группы симметрии и их приложения . Нью-Йорк: Академическая пресса. OCLC 589081 . Архивировано из оригинала 17 февраля 2010 г. Проверено 28 сентября 2009 г.
- ^ «Теория многомерных групп» . Архивировано из оригинала 23 июля 2012 г. Проверено 16 апреля 2013 г.
- ^ «2.6 Отражательная симметрия» . Фонд СК-12 . Проверено 6 декабря 2019 г.
- ^ Вейль, Герман (1982) [1952]. Симметрия . Принстон: Издательство Принстонского университета. ISBN 0-691-02374-3 .
- ^ Коуин, Стивен С.; Доти, Стивен Б. (2007). Тканевая механика . Спрингер. п. 152 . ISBN 9780387368252 .
- ^ Калдекотт, Стратфорд (2009). Красота ради истины: о возрождении образования . Бразос Пресс. п. 70.
- ^ Басарир, Том (2011). Математика для учителей начальных классов (5-е изд.). Cengage Обучение. п. 499.
- ^ Джонсон, Н. В. Джонсон (2018). «11: Конечные группы симметрии». Геометрии и преобразования . Издательство Кембриджского университета.
- ^ Хертрих-Жеромин, Удо (2003). Введение в дифференциальную геометрию Мёбиуса . Издательство Кембриджского университета.
- ^ Дик, Таммо (2008). Алгебраическая топология . Европейское математическое общество. стр. 261 . ISBN 9783037190487 .
- ^ Уильям Х. Баркер, Непрерывная симметрия Роджера Хоу: от Евклида до Кляйна (электронная книга Google) American Mathematical Soc
- ^ В.М. Гибсон и Б.Р. Поллард (1980). Принципы симметрии в физике элементарных частиц . Издательство Кембриджского университета. стр. 120–122. ISBN 0-521-29964-0 .
- ^ Владимир Г. Иванцевич, Тияна Т. Иванцевич (2005) Natural Biodynamics World Scientific
- ^ Певец, Дэвид А. (1998). Геометрия: плоскость и фантазия . Springer Science & Business Media.
- ^ Джоши, AW (2007). Элементы теории групп для физиков . Нью Эйдж Интернэшнл. стр. 111 и далее.
- ^ Хартшорн, Робин (2000). Геометрия: Евклид и не только . Springer Science & Business Media.
- ^ Косманн-Шварцбах, Иветт (2010). Теоремы Нётер: законы инвариантности и сохранения в двадцатом веке . Источники и исследования по истории математики и физических наук. Спрингер-Верлаг . ISBN 978-0-387-87867-6 .
- ^ Стенгер, Виктор Дж. (2000) и Махоу Широ (2007). Вечная реальность . Книги Прометея. Особенно глава 12. Нетехническая.
- ^ Мартин, Джордж Э. (1982), Геометрия преобразований: введение в симметрию , Тексты для студентов по математике , Springer, стр. 64, ISBN 9780387906362 .
- ^ Роберт О. Гулд, Штеффен Борхардт-Отт (2011) Кристаллография: введение Springer Science & Business Media
- ^ Боттема, О. и Б. Рот, Теоретическая кинематика, Dover Publications (сентябрь 1990 г.)
- ^ Джордж Р. МакГи (2006) Геометрия эволюции: адаптивные ландшафты и теоретические морфопространства Cambridge University Press, стр.64
- ^ Урсын, Анна (2012). «Глава 12. Визуальный твит: визуальные высказывания, вдохновленные природой». В Урсине, Анна (ред.). Биологические вычисления в искусстве: научные данные через графику . IGI Global. стр. 207–239. См. раздел «Справочная информация о понятии симметрии применительно к геометрии», с. 209 .
- ^ Синден, Ричард Р. (1994). Структура и функции ДНК . Профессиональное издательство Персидского залива. п. 101. ИСБН 9780126457506 .
- ^ Чарльз Ховард Хинтон (1906) Четвертое измерение (электронная книга Google) С. Зонненшайн и компания, стр.223
- ^ HSM Coxeter (1961,9) Введение в геометрию , §5 Подобие в евклидовой плоскости, стр. 67–76, §7 Изометрия и подобие в евклидовом пространстве, стр 96–104, John Wiley & Sons .
- ^ Уильям Терстон. Трехмерная геометрия и топология. Том. 1 . Под редакцией Сильвио Леви. Принстонская математическая серия, 35. Издательство Принстонского университета, Принстон, Нью-Джерси, 1997. x+311 стр. ISBN 0-691-08304-5
- ^ Кляйн, Феликс , 1872. «Сравнительный обзор последних исследований в области геометрии», Mathematical Annals, 43 (1893), стр. 63–100 (также: Gesammelte Abh. Vol. 1, Springer, 1921, стр. 460– 497).
- Английский перевод Меллен Хаскелл появился в Bull. Нью-Йорк Математика. Сок 2 (1892–1893): 215–249.
- ^ Тянь Юй Цао Концептуальные основы квантовой теории поля Издательство Кембриджского университета стр. 154-155
- ^ Гуйе, Жан-Франсуа (1996). Физика и фрактальные структуры . Париж/Нью-Йорк: Массон Спрингер. ISBN 978-0-387-94153-0 .

