Наследственно конечное множество

В математике и теории множеств наследственно конечные множества определяются как конечные множества , все элементы которых являются наследственно конечными множествами. Другими словами, само множество конечно, и все его элементы являются конечными множествами, рекурсивно вплоть до пустого множества .

Формальное определение

Рекурсивное наследственно определение обоснованных конечных множеств выглядит следующим образом:

Базовый случай : пустое множество является наследственно конечным множеством.

Правило рекурсии : Если $a_{1},\dots a_{k}$ наследственно конечны, то и $\{a_{1},\dots a_{k}\}$.

Наследственно конечными являются только множества, которые могут быть построены конечным числом применений этих двух правил.

Представительство

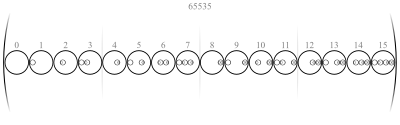
Этот класс множеств естественным образом ранжируется по количеству пар скобок, необходимых для представления множеств:

• $\{\}$ (т.е. $\emptyset$, порядковый номер Неймана "0")
• $\{\{\}\}$ (т.е. $\{\emptyset \}$ или $\{0\}$, порядковый номер Неймана "1")
• $\{\{\{\}\}\}$
• $\{\{\{\{\}\}\}\}$ а потом еще $\{\{\},\{\{\}\}\}$ (т.е. $\{0,1\}$, ординал Неймана "2"),
• $\{\{\{\{\{\}\}\}\}\}$, $\{\{\{\},\{\{\}\}\}\}$ а также $\{\{\},\{\{\{\}\}\}\}$,
• ... наборы, представленные $6$ пары скобок, например $\{\{\{\{\{\{\}\}\}\}\}\}$. Таких наборов шесть.
• ... наборы, представленные $7$ пары скобок, например $\{\{\{\{\{\{\{\}\}\}\}\}\}\}$. Таких наборов двенадцать.
• ... наборы, представленные $8$ пары скобок, например $\{\{\{\{\{\{\{\{\}\}\}\}\}\}\}\}$ или $\{\{\},\{\{\}\},\{\{\},\{\{\}\}\}\}$ (т.е. $\{0,1,2\}$, порядковый номер Неймана "3")
• ... и т. д.

Таким образом, количество наборов с $n$ пары кронштейнов есть

1, 1, 1, 2, 3, 6, 12, 25, 52, 113, 247, 548, 1226, 2770, 6299, 14426, ...

Обсуждение

Набор $\{\{\},\{\{\{\}\}\}\}$ является примером такого наследственно конечного множества, как и пустое множество $\{\}$, как было отмечено. С другой стороны, множества $\{7,{\mathbb {N} },\pi \}$ или $\{3,\{{\mathbb {N} }\}\}$ являются примерами конечных множеств, которые не являются наследственно конечными. Например, первое не может быть наследственно конечным, поскольку содержит в качестве элемента хотя бы одно бесконечное множество, когда ${\mathbb {N} }=\{0,1,2,\dots \}$.

Класс всех наследственно конечных множеств обозначается через $H_{\aleph _{0}}$, что означает, что мощность каждого члена меньше, чем $\aleph _{0}$. (Аналогично класс наследственно счетных множеств обозначается через $H_{\aleph _{1}}$.) $H_{\aleph _{0}}$ находится в биективном соответствии с $\aleph _{0}$.Его также можно обозначить $V_{\omega }$, что обозначает $\omega$Этап Вселенной фон Неймана . Итак, вот это счетное множество.

Модели

Кодирование Аккермана

В 1937 году Вильгельм Акерманн ввел кодировку наследственно конечных множеств как натуральных чисел. Оно определяется функцией $f\colon H_{\aleph _{0}}\to \omega$ который отображает каждое наследственно конечное множество в натуральное число, заданное следующим рекурсивным определением:

$\displaystyle f(a)=\sum _{b\in a}2^{f(b)}$

Например, пустой набор $\{\}$ не содержит элементов и поэтому отображается в пустую сумму , то есть в число ноль . С другой стороны, множество с различными членами $a,b,c,\dots$ отображается на $2^{f(a)}+2^{f(b)}+2^{f(c)}+\ldots$.

Обратное имеет вид

$\displaystyle f^{-1}\colon \omega \to H_{\aleph _{0}}$

$\displaystyle f^{-1}(i)=\{f^{-1}(j)\mid {\text{BIT}}(i,j)=1\}$

где BIT обозначает предикат BIT .

Кодирование Аккермана можно использовать для построения модели финитной теории множеств в натуральных числах. Точнее, $(\mathbb {N} ,{\text{BIT}}^{\top })$ (где ${\text{BIT}}^{\top }$ является обратным отношением ${\text{BIT}}$, меняя местами два аргумента) модели теории множеств Цермело–Френкеля ZF без аксиомы бесконечности . Здесь каждое натуральное число моделирует множество, а ${\text{BIT}}$ Отношение моделирует отношение принадлежности между множествами.

Графовые модели

Класс $H_{\aleph _{0}}$ можно видеть, что они находятся в точном соответствии с классом корневых деревьев , а именно с деревьями без нетривиальных симметрий (т.е. единственным автоморфизмом является тождество): Корневая вершина соответствует скобке верхнего уровня. $\{\dots \}$ и каждое ребро ведет к элементу (еще одному такому набору), который сам по себе может действовать как корневая вершина. Автоморфизм этого графа не существует, что соответствует тому факту, что идентифицируются равные ветви (например, $\{t,t,s\}=\{t,s\}$, упрощая перестановку двух подграфов формы $t$).Эта графовая модель позволяет реализовать ZF без бесконечности в качестве типов данных и, таким образом, интерпретировать теорию множеств в выразительных теориях типов .

графов Существуют модели для ZF, а также теории множеств, отличные от теории множеств Цермело, такие как недостаточно обоснованные теории. Такие модели имеют более сложную структуру края.

В теории графов граф, вершины которого соответствуют наследственно конечным множествам, а ребра соответствуют членству в множестве, является графом Радо или случайным графом.

Аксиоматизации

Теории конечных множеств

В общепринятых аксиоматических подходах теории множеств пустое множество $\{\}$ также представляет собой первое порядковое число фон Неймана , обозначаемое $0$. Все конечные ординалы фон Неймана действительно наследственно конечны, как и класс множеств, представляющих натуральные числа. Другими словами, $H_{\aleph _{0}}$ включает каждый элемент стандартной модели натуральных чисел и теорию множеств, выражающую $H_{\aleph _{0}}$ должен содержать все это.

Теперь обратите внимание, что арифметика Робинсона уже может быть интерпретирована в ST , очень маленькой подтеории теории множеств Цермело Z. ⁻ с его аксиомами, заданными экстенсиональностью , пустым множеством и дополнением . $H_{\aleph _{0}}$ имеет конструктивную аксиоматизацию, включающую эти аксиомы и, например, индукцию множества и замену .

Аксиоматически характеризуя теорию наследственно конечных множеств, можно добавить отрицание аксиомы бесконечности, доказав тем самым, что аксиома бесконечности не является следствием других аксиом ZF.

ЗФ

$~V_{4}~$ представлен кружками вместо фигурных скобок     

Наследственно конечные множества являются подклассом вселенной фон Неймана . Здесь обозначен класс всех обоснованных наследственно конечных множеств $V_{\omega }$. Обратите внимание, что в данном контексте это также набор.

Если мы обозначим через $\wp (S)$ силовой набор ​ $S$и по $V_{0}$ пустое множество, тогда $V_{\omega }$ можно получить, установив $V_{i+1}=\wp (V_{i})$ для каждого целого числа $i\geq 0$. Таким образом, $V_{\omega }$ может быть выражено как

$\displaystyle V_{\omega }=\bigcup _{k=0}^{\infty }V_{k}$

и все его элементы конечны.

существует только счетное число: Эта формулировка еще раз показывает, что наследственно конечных множеств $V_{n}$ конечно для любого конечного $n$, его мощность равна $2\uparrow \uparrow (n-1)$ в обозначении Кнута, направленном вверх (башня из $n-1$ степени двойки), а объединение счетного числа конечных множеств счетно.

Эквивалентно, множество наследственно конечно тогда и только тогда, когда его транзитивное замыкание конечно.

См. также

• Конструктивная теория множеств
• Конечный набор
• Наследственный набор
• Наследственно счетное множество
• Наследственная собственность
• Деревья с корнями