Теорема Декарта

Чтобы узнать о других значениях, см. теорему Декарта (значения) .

Поцелуи кругами. Даны три взаимно касающиеся окружности ( черный ), существует, вообще говоря, два варианта ответа ( красный ) о том, какой радиус может иметь четвертая касательная окружность.

В геометрии утверждает , теорема Декарта что для каждых четырех целующихся или взаимно радиусы кругов касающихся кругов удовлетворяют определенному квадратному уравнению . Решив это уравнение, можно построить четвертую окружность, касающуюся трех заданных взаимно касающихся окружностей. Теорема названа в честь Рене Декарта , сформулировавшего ее в 1643 году.

Стихотворение Фредерика Содди » 1936 года « Точный поцелуй резюмирует теорему в терминах изгибов (обратных радиусов со знаком) четырех кругов:

Сумма квадратов всех четырех изгибов
Является половиной квадрата их суммы

Особые случаи теоремы применяются, когда одна или две окружности заменяются прямой линией (с нулевым изгибом) или когда изгибы представляют собой целые или квадратные числа . Версия теоремы с использованием комплексных чисел позволяет вычислять центры кругов, а не только их радиусы. При соответствующем определении кривизны теорема также применима в сферической геометрии и гиперболической геометрии . В более высоких измерениях аналогичное квадратное уравнение применимо к системам попарно касательных сфер или гиперсфер.

История

Геометрические задачи, связанные с касательными окружностями, решались на протяжении тысячелетий. В Древней Греции третьего века до нашей эры Аполлоний Пергский посвятил этой теме целую книгу Ἐπαφαί [ Тангенсии ]. Он был утерян и известен в основном благодаря описанию его содержания Паппом Александрийским и фрагментарным ссылкам на него в средневековой исламской математике . Однако греческая геометрия была в основном сосредоточена на построении линейки и циркуля . Например, проблема Аполлония , тесно связанная с теоремой Декарта, требует построения окружности, касающейся трех данных окружностей, которые сами не обязательно должны касаться. Вместо этого теорема Декарта формулируется с использованием алгебраических отношений между числами, описывающими геометрические формы. Это характерно для аналитической геометрии — области, впервые созданной Рене Декартом и Пьером де Ферма в первой половине 17 века.

Декарт кратко обсудил проблему касательной окружности в 1643 году в двух письмах принцессе Елизавете Пфальцской . Декарт первоначально поставил перед принцессой проблему Аполлония. После того, как частичные результаты Элизабет показали, что аналитическое решение всей проблемы было бы слишком утомительным, он упростил задачу до случая, когда три заданных окружности касаются друг друга, и при решении этой упрощенной задачи он придумал уравнение, описывающее связь между радиусы или кривизны четырех попарно касающихся окружностей. Этот результат стал известен как теорема Декарта. Декарт не привел аргументов, с помощью которых он нашел это соотношение.

Японская математика часто касалась задач, связанных с окружностями и их касаниями. и японский математик Ямадзи Нусидзуми сформулировал форму теоремы Декарта о круге в 1751 году. Как и Декарт, он выразил ее как полиномиальное уравнение относительно радиусов, а не их кривизны. Частный случай этой теоремы для одной прямой и трех окружностей был записан на японской табличке сангаку 1824 года.

Теорема Декарта была заново открыта в 1826 году Якобом Штайнером . в 1842 году Филип Бикрофт, и в 1936 году Фредериком Содди . Содди решил оформить свою версию теоремы в виде стихотворения «Точный поцелуй » и опубликовал его в журнале Nature . Круги поцелуев в этой задаче иногда называют кругами Содди . Содди также распространил теорему на сферы: а в другом стихотворении описана цепочка из шести сфер, каждая из которых касается своих соседей, и трех данных взаимно касающихся сфер, конфигурация, которая теперь называется гекслетом Содди . Торольд Госсет и некоторые другие расширили теорему и стихотворение до произвольных размеров; Версия Госсета была опубликована в следующем году. Это обобщение иногда называют теоремой Содди – Госсета . хотя и гекслет, и трехмерная версия были известны ранее, в сангаку и в работе Роберта Лахлана 1886 года.

Было опубликовано множество доказательств теоремы. Доказательство Штейнера использует цепи Паппуса и теорему Вивиани . Доказательства Филипа Бикрофта и Х.С.М. Коксетера включают еще четыре окружности, проходящие через тройки касаний исходных трех окружностей; Коксетер также предоставил доказательство с использованием инверсной геометрии . Дополнительные доказательства включают аргументы, основанные на симметрии, вычислениях во внешней алгебре или алгебраических манипуляциях с формулой Герона (см. § Круги Содди треугольника ). Результат также следует из наблюдения, что определитель Кэли – Менгера четырех копланарных центров окружностей равен нулю.

Заявление

Здесь, поскольку все три окружности касаются друг друга в одной точке, теорема Декарта неприменима.

окружностей Теорему Декарта проще всего сформулировать в терминах кривизны . ( Знаковая кривизна или изгиб ) окружности определяется как $k=\pm 1/r$, где $r$ это его радиус. Чем больше круг, тем меньше величина его кривизны, и наоборот. Вход в систему $k=\pm 1/r$ (в лице $\pm$ символ) положителен для окружности, касающейся снаружи других окружностей. Для внутренней касательной окружности, описывающей другие окружности, знак отрицательный. Если прямая линия считается вырожденным кругом с нулевой кривизной (и, следовательно, бесконечным радиусом), теорема Декарта также применима к линии и трем окружностям, которые все три касаются друг друга (см. Обобщенный круг ).

Для четырех окружностей, касающихся друг друга в шести различных точках, с кривизной $k_{i}$ для $i=1,\dots ,4$, теорема Декарта гласит:

$(k_{1}+k_{2}+k_{3}+k_{4})^{2}=2\,(k_{1}^{2}+k_{2}^{2}+k_{3}^{2}+k_{4}^{2}).$ $(1)$

Если одну из четырех кривизн считать переменной, а остальные постоянными, то это квадратное уравнение .Чтобы найти радиус четвертого круга, касательного трех заданных кругов поцелуев, квадратное уравнение можно решить как

$k_{4}=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}}}.$ $(2)$

The $\pm$ Символ указывает, что в общем случае это уравнение имеет два решения, и любая тройка касательных окружностей имеет две касательные окружности (или вырожденные прямые линии). Критерии, специфичные для конкретной проблемы, могут отдавать предпочтение одному из этих двух решений перед другим в любой конкретной проблеме.

Теорема не применима к системам окружностей, в которых более двух окружностей касаются друг друга в одной точке. Это требует, чтобы точки касания были различны. Когда более двух окружностей касаются одной точки, таких кругов может быть бесконечно много с произвольной кривизной; см. карандаш кругов .

Нахождение центров кругов

Чтобы полностью определить окружность, необходимо знать не только ее радиус (или кривизну), но и ее центр. Соответствующее уравнение выражается наиболее наглядно, если декартовы координаты $(x,y)$ интерпретируются как комплексное число $z=x+iy$. Тогда уравнение выглядит аналогично теореме Декарта и поэтому называется комплексной теоремой Декарта . Даны четыре круга кривизны. $k_{i}$ и центры $z_{i}$ для $i\in \{1,2,3,4\}$, имеет место следующее равенство в дополнение к уравнению (1) :

$(k_{1}z_{1}+k_{2}z_{2}+k_{3}z_{3}+k_{4}z_{4})^{2}=2\,(k_{1}^{2}z_{1}^{2}+k_{2}^{2}z_{2}^{2}+k_{3}^{2}z_{3}^{2}+k_{4}^{2}z_{4}^{2}).$ $(3)$

Один раз $k_{4}$ было найдено с помощью уравнения (2) , можно приступить к расчету $z_{4}$ решив уравнение (3) как квадратное уравнение, что приведет к форме, аналогичной уравнению (2) :

$$z_{4}={\frac {z_{1}k_{1}+z_{2}k_{2}+z_{3}k_{3}\pm 2{\sqrt {k_{1}k_{2}z_{1}z_{2}+k_{2}k_{3}z_{2}z_{3}+k_{1}k_{3}z_{1}z_{3}}}}{k_{4}}}.$$

Опять же, в целом есть два решения для $z_{4}$ соответствующие двум решениям для $k_{4}$. Знак плюс/минус в приведенной выше формуле для $z_{4}$ не обязательно соответствует знаку плюс/минус в формуле $k_{4}$.

Особые случаи

Все три конгруэнтных взаимно касающихся окружности кривизны k = 1/√3 касаются двух окружностей соответствующей кривизны k = √3 ± 2 .

Три одинаковых круга

Когда три из четырех кругов конгруэнтны, их центры образуют равносторонний треугольник, как и точки их касания. Две возможности четвертой окружности, касающейся всех трех, концентричны, и уравнение (2) сводится к

$$k_{4}=(3\pm 2{\sqrt {3}})k_{1}.$$

Одна или несколько прямых линий

Теорема Декарта по-прежнему применима, когда один из кругов заменяется прямой линией нулевой кривизны.

Если одну из трех окружностей заменить прямой, касательной к остальным окружностям , то ее кривизна равна нулю и выпадает из уравнения (1) . Например, если $k_{3}=0$, то уравнение (1) можно факторизовать как

$${\begin{aligned}&{\bigl (}{\sqrt {k_{1}}}+{\sqrt {k_{2}}}+{\sqrt {k_{4}}}{\bigr )}{\bigl (}{{\sqrt {k_{2}}}+{\sqrt {k_{4}}}-{\sqrt {k_{1}}}}{\bigr )}\\[3mu]&\quad {}\cdot {\bigl (}{\sqrt {k_{1}}}+{\sqrt {k_{4}}}-{\sqrt {k_{2}}}{\bigr )}{\bigl (}{\sqrt {k_{1}}}+{\sqrt {k_{2}}}-{\sqrt {k_{4}}}{\bigr )}=0,\end{aligned}}$$

и уравнение (2) упрощается до

$$k_{4}=k_{1}+k_{2}\pm 2{\sqrt {k_{1}k_{2}}}.$$

Извлечение квадратного корня из обеих частей приводит к другой альтернативной формулировке этого случая (с $k_{1}\geq k_{2}$),

$${\sqrt {k_{4}}}={\sqrt {k_{1}}}\pm {\sqrt {k_{2}}},$$

который был описан как «своего рода безумная версия теоремы Пифагора ».

Если две окружности заменяются линиями, касание между двумя замененными окружностями становится параллелизмом между двумя замещающими линиями. В этом случае с $k_{2}=k_{3}=0$, уравнение (2) сводится к тривиальному

$$\displaystyle k_{4}=k_{1}.$$

Это соответствует наблюдению, что для того, чтобы все четыре кривые оставались взаимно касающимися, два других круга должны быть конгруэнтны.

Целочисленные кривизны

Аполлонова прокладка с целочисленной кривизной, образованная четырьмя взаимно касающимися окружностями с кривизной -10 (внешний круг), 18, 23 и 27.

Когда все четыре касательные окружности, описанные уравнением (2), имеют целочисленную кривизну, альтернативная четвертая окружность, описываемая вторым решением уравнения, также должна иметь целочисленную кривизну. Это связано с тем, что оба решения отличаются от целого числа на квадратный корень из целого числа, и поэтому любое решение может быть целым числом только в том случае, если этот квадратный корень и, следовательно, другое решение также являются целым числом. Каждые четыре целых числа, удовлетворяющие уравнению теоремы Декарта, образуют кривизну четырех касательных окружностей. Целые четверки этого типа также тесно связаны с героновыми треугольниками , треугольниками с целыми сторонами и площадью.

Начав с любых четырех взаимно касающихся окружностей, и неоднократно заменяя одну из четырех ее альтернативным решением ( прыжком Вьета ), всеми возможными способами, приводите к системе из бесконечного числа касательных окружностей, называемой аполлоновой прокладкой . Когда исходные четыре круга имеют целочисленную кривизну, то же самое имеет и каждая замена, и, следовательно, все круги в прокладке имеют целочисленную кривизну. Любые четыре касательных окружности с целочисленной кривизной принадлежат ровно одной такой прокладке, однозначно описываемой ее корневой четверкой из четырех крупнейших окружностей и четырех наименьших кривизн. Эту четверку можно найти, начиная с любой другой четверки из той же прокладки, многократно заменяя наименьший круг большим, решая то же уравнение Декарта, до тех пор, пока такое сокращение не станет возможным.

Корневая четверка называется примитивной , если она не имеет нетривиального общего делителя . Любую примитивную корневую четверку можно найти факторизацией суммы двух квадратов: $n^{2}+m^{2}=de$, как четверка $(-n,\,d+n,\,e+n,\,d+e+n-2m)$. Чтобы быть примитивным, он должен удовлетворять дополнительным условиям $\gcd(n,d,e)=1$, и $-n\leq 0\leq 2m\leq d\leq e$. Факторизацию суммы двух квадратов можно получить, используя теорему о сумме двух квадратов . Любая другая целочисленная аполлонова прокладка может быть образована путем умножения примитивной корневой четверки на произвольное целое число, а любая четверка в одной из этих прокладок (то есть любое целочисленное решение уравнения Декарта) может быть образована путем обращения процесса замены, используемого для нахождения корень четверки. Например, прокладка с корневой четверкой $(-10,18,23,27)$, показанный на рисунке, генерируется таким образом из факторизованной суммы двух квадратов $10^{2}+2^{2}=8\cdot 13$.

Фордовые круги

Круги Форда в единичном интервале

Основная статья: Круг Форда

Частные случаи одной прямой и целочисленной кривизны объединяются в кругах Форда . Это бесконечное семейство окружностей, касающихся $x$-ось декартовой системы координат в ее рациональных точках. Каждая фракция $p/q$ (в самых простых терминах) имеет окружность, касающуюся линии в точке $(p/q,0)$ с кривизной $2q^{2}$. Три из этих кривизн вместе с нулевой кривизной оси удовлетворяют условиям теоремы Декарта всякий раз, когда знаменатели двух соответствующих дробей суммируются со знаменателем третьей. Два круга Форда для дробей $p/q$ и $r/s$ (оба в самых низких терминах) касаются , когда $|ps-qr|=1$. Когда они касаются друг друга, они образуют четверку касательных окружностей с $x$-ось и с кругом для их медианы $(p+r)/(q+s)$.

Круги Форда относятся к особой аполлоновой прокладке с корневым четвериком. $(0,0,1,1)$, ограниченный между двумя параллельными прямыми, которые можно принять за $x$-ось и линия $y=1$. Это единственная аполлоническая прокладка, содержащая прямую линию и не ограниченная кругом отрицательной кривизны. Круги Форда — это круги в этой прокладке, которые касаются $x$-ось .

Геометрическая прогрессия

Основная статья: локсодромная последовательность касательных окружностей Кокстера

Локсодромная последовательность касательных окружностей Кокстера . Каждый круг помечен целым числом i — его положением в последовательности; он имеет радиус ρ ^я и кривизна ρ ^-я .

Если предположить, что четыре радиуса окружностей в теореме Декарта находятся в геометрической прогрессии с соотношением $\rho$, кривизны также находятся в той же прогрессии (в обратном порядке). Подстановка этого соотношения в теорему дает уравнение

$$2(1+\rho ^{2}+\rho ^{4}+\rho ^{6})=(1+\rho +\rho ^{2}+\rho ^{3})^{2},$$

которое имеет только одно действительное решение больше единицы, соотношение

$$\rho =\varphi +{\sqrt {\varphi }}\approx 2.89005\ ,$$

где $\varphi$ это золотое сечение . Если одну и ту же прогрессию продолжить в обоих направлениях, каждые четыре последовательных числа описывают круг, подчиняющийся теореме Декарта. Полученная двусторонняя геометрическая прогрессия кругов может быть организована в единый спиральный узор из касательных кругов , называемый локсодромной последовательностью касательных кругов Коксетера . Впервые он был описан вместе с аналогичными конструкциями в более высоких измерениях Х.С.М. Коксетером в 1968 году.

Дерновые круги треугольника

Основная статья: Дерновые круги треугольника

Любой треугольник на плоскости имеет три касательные снаружи окружности с центрами в его вершинах. Сдача в аренду $A,B,C$ быть тремя точками, $a,b,c$ - длины противоположных сторон, а ${\textstyle s={\tfrac {1}{2}}(a+b+c)}$ быть полупериметром , эти три круга имеют радиусы $s-a,s-b,s-c$. По теореме Декарта еще две окружности, иногда называемые окружностями Содди к этим трем окружностям касаются . Они разделены вписанным кругом , одним внутренним и одним внешним. Теорему Декарта можно использовать, чтобы показать, что кривизна внутреннего круга Содди равна ${\textstyle (4R+r+2s)/\Delta }$, где $\Delta$ площадь треугольника, $R$ это его радиус окружности , а $r$ это его радиус . Внешний круг Содди имеет кривизну. ${\textstyle (4R+r-2s)/\Delta }$. Внутренняя кривизна всегда положительна, но внешняя кривизна может быть положительной, отрицательной или нулевой. Треугольники, внешняя окружность которых вырождается в прямую линию с нулевой кривизной, называются «соддиевыми треугольниками».

Четыре треугольника с вершинами в центрах кругов Содди.

Одно из многих доказательств теоремы Декарта основано на этой связи с геометрией треугольника и на формуле Герона для определения площади треугольника как функции длин его сторон.Если три окружности касаются снаружи, радиусы $r_{1},r_{2},r_{3},$ затем их центры $P_{1},P_{2},P_{3}$ сформировать вершины треугольника с длинами сторон $r_{1}+r_{2},$ $r_{1}+r_{3},$ и $r_{2}+r_{3},$ и полупериметр $r_{1}+r_{2}+r_{3}.$ По формуле Герона этот треугольник $\triangle P_{1}P_{2}P_{3}$ имеет площадь

$${\sqrt {r_{1}r_{2}r_{3}(r_{1}+r_{2}+r_{3})}}.$$

Теперь рассмотрим внутренний круг Содди радиусом $r_{4},$ с центром в точке $P_{4}$ внутри треугольника. Треугольник $\triangle P_{1}P_{2}P_{3}$ можно разбить на три меньших треугольника $\triangle P_{1}P_{2}P_{4},$ $\triangle P_{4}P_{2}P_{3},$ и $\triangle P_{1}P_{4}P_{3},$ площади которых можно получить заменой $r_{4}$ для одного из других радиусов в приведенной выше формуле площади. Площадь первого треугольника равна сумме этих трёх площадей:

$${\begin{aligned}{\sqrt {r_{1}r_{2}r_{3}(r_{1}+r_{2}+r_{3})}}={}&{\sqrt {r_{1}r_{2}r_{4}(r_{1}+r_{2}+r_{4})}}+{}\\&{\sqrt {r_{1}r_{3}r_{4}(r_{1}+r_{3}+r_{4})}}+{}\\&{\sqrt {r_{2}r_{3}r_{4}(r_{2}+r_{3}+r_{4})}}.\end{aligned}}$$

Тщательные алгебраические манипуляции показывают, что эта формула эквивалентна уравнению (1) , теореме Декарта.

Здесь внешний центр Содди лежит вне треугольника.

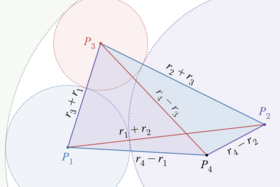
Этот анализ охватывает все случаи, когда четыре окружности касаются снаружи; один всегда является внутренним кругом Содди трех других. Случаи, когда одна из окружностей внутренне касается трех других и образует их внешнюю окружность Содди, аналогичны. И снова четыре центра $P_{1},P_{2},P_{3},P_{4}$ образуют четыре треугольника, но (позволяя $P_{4}$ быть центром внешнего круга Содди) стороны треугольника, инцидентные $P_{4}$ имеют длины, являющиеся разностью радиусов, $r_{4}-r_{1},$ $r_{4}-r_{1},$ и $r_{4}-r_{3},$ а не суммы. $P_{4}$ может лежать внутри или снаружи треугольника, образованного тремя другими центрами; когда он находится внутри, площадь этого треугольника равна сумме площадей трех других треугольников, как указано выше. Когда он находится снаружи, четырехугольник, образованный четырьмя центрами, можно разделить диагональю на два треугольника двумя разными способами, давая равенство между суммой двух площадей треугольника и суммой двух других площадей треугольника. В каждом случае уравнение площади сводится к теореме Декарта. Этот метод не применим непосредственно к случаям, когда одна из окружностей вырождается в прямую, но их можно рассматривать как предельный случай окружностей.

Обобщения

Произвольные четырехокружные конфигурации

Теорему Декарта можно выразить в виде матричного уравнения, а затем обобщить на другие конфигурации четырех ориентированных кругов, изменив матрицу. Позволять $\mathbf {k}$ будет вектор-столбцом четырех кривизн круга и пусть $\mathbf {Q}$ — симметричная матрица , коэффициенты которой $q_{i,j}$ представляют относительную ориентацию между i -м и j -м ориентированными кругами в точке их пересечения: $$\mathbf {Q} ={\begin{bmatrix}{\phantom {-}}1&-1&-1&-1\\-1&{\phantom {-}}1&-1&-1\\-1&-1&{\phantom {-}}1&-1\\-1&-1&-1&{\phantom {-}}1\\\end{bmatrix}},\qquad \mathbf {Q} ^{-1}={\frac {1}{4}}{\begin{bmatrix}{\phantom {-}}1&-1&-1&-1\\-1&{\phantom {-}}1&-1&-1\\-1&-1&{\phantom {-}}1&-1\\-1&-1&-1&{\phantom {-}}1\\\end{bmatrix}}.$$

Тогда уравнение (1) можно переписать в виде матричного уравнения

$$\mathbf {k} ^{\mathsf {T}}\mathbf {Q} ^{-1}\mathbf {k} =0.$$

Как обобщение теоремы Декарта, модифицированная симметричная матрица $\mathbf {Q}$ может представлять любую желаемую конфигурацию из четырех кругов, заменяя каждый коэффициент наклоном $q_{i,j}$ между двумя кругами, определяемыми как

$$q_{i,j}={\frac {r_{i}^{2}+r_{j}^{2}-d_{i,j}^{2}}{2r_{i}r_{j}}},$$

где $r_{i},r_{j}$ - соответствующие радиусы кругов, а $d_{i,j}$ – евклидово расстояние между их центрами. Когда круги пересекаются, $q_{i,j}=\cos(\theta _{i,j})$, косинус угла пересечения окружностей. Наклон, иногда называемый обратным расстоянием , равен $1$ когда окружности касаются и ориентированы одинаково в точке касания, $-1$ когда две окружности касаются и ориентированы противоположно в точке касания, $0$ для ортогональных окружностей вне интервала $[-1,1]$ для непересекающихся кругов и $\infty$ в пределе, когда одна окружность вырождается в точку.

Уравнение $\mathbf {k} ^{\mathsf {T}}\mathbf {Q} ^{-1}\mathbf {k} =0$ выполняется для любой произвольной конфигурации четырех окружностей на плоскости при условии, что $\mathbf {Q}$ – соответствующая матрица попарных наклонов.

Сферическая и гиперболическая геометрия

Частный случай теоремы Декарта о сфере имеет три круга радиуса 60 ° ( k = 1/√3 , синий цвет), для которых оба круга, касающиеся всех трех (зеленый цвет), имеют одинаковый радиус ( 30 ° , k = √ 3 ).

Теорема Декарта обобщается на касающиеся друг друга большие или малые круги в сферической геометрии, если кривизна $j$круг определяется как ${\textstyle k_{j}=\cot \rho _{j},}$ геодезическая кривизна круга относительно сферы, равная котангенсу ориентированного внутреннего радиуса $\rho _{j}.$ Затем:

$$(k_{1}+k_{2}+k_{3}+k_{4})^{2}=2(k_{1}^{2}+k_{2}^{2}+k_{3}^{2}+k_{4}^{2})+4.$$

Решая одну из кривизн через три других,

$$k_{4}=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}-1}}.$$

В качестве матричного уравнения

$$\mathbf {k} ^{\mathsf {T}}\mathbf {Q} ^{-1}\mathbf {k} =-1.$$

Количество $1/k_{j}=\tan \rho _{j}$ - «стереографический диаметр» малого круга. Это евклидова длина диаметра в стереографически проецируемой плоскости, когда некоторая точка окружности проецируется в начало координат. Для большого круга такая стереографическая проекция представляет собой прямую линию, проходящую через начало координат, поэтому $k_{j}=0$.

Четыре обобщенных круга, являющиеся источником модели диска Пуанкаре гиперболической плоскости: круг (синий), орицикл (красный), гиперцикл (фиолетовый) и геодезический (зеленый). Граница идеальных точек изображается пунктирной линией, а заштрихованная область находится вне плоскости.

Аналогично, теорема обобщается на взаимно касающиеся круги в гиперболической геометрии, если кривизна $j$-й цикл определяется как ${\textstyle k_{j}=\coth \rho _{j},}$ геодезическая кривизна окружности относительно гиперболической плоскости, гиперболический котангенс ориентированного внутреннего радиуса $\rho _{j}.$ Затем:

$$(k_{1}+k_{2}+k_{3}+k_{4})^{2}=2(k_{1}^{2}+k_{2}^{2}+k_{3}^{2}+k_{4}^{2})-4.$$

Решая одну из кривизн через три других,

$$k_{4}=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}+1}}.$$

В качестве матричного уравнения

$$\mathbf {k} ^{\mathsf {T}}\mathbf {Q} ^{-1}\mathbf {k} =1.$$

Эта формула также справедлива для взаимно касательных конфигураций в гиперболической геометрии, включая гиперциклы и орициклы , если $k_{j}$ - геодезическая кривизна цикла относительно гиперболической плоскости, обратная стереографическому диаметру цикла. Это диаметр в стереографической проекции ( модель диска Пуанкаре ), когда одна конечная точка диаметра проецируется в начало координат. Гиперциклы не имеют четко определенного центра или внутреннего радиуса, а орициклы имеют идеальную точку для центра и бесконечный внутренний радиус, но $|k_{j}|>1$ для гиперболического круга, $|k_{j}|=1$ для орицикла, $|k_{j}|<1$ для гиперцикла, и $k_{j}=0$ для геодезической .

Высшие измерения

Гекслет Содди . Любая пара соседних зеленых сфер вместе с двумя красными сферами и внешней серой сферой удовлетворяет трехмерному случаю теоремы Декарта.

В $n$В -мерном евклидовом пространстве максимальное число взаимно касательных гиперсфер равно $n+2$. Например, в трехмерном пространстве пять сфер могут касаться друг друга. Кривизны гиперсфер удовлетворяют

$${\biggl (}\sum _{i=1}^{n+2}k_{i}{\biggr )}^{\!2}=n\,\sum _{i=1}^{n+2}k_{i}^{2}$$

с делом $k_{i}=0$ соответствующий плоской гиперплоскости, обобщающий двумерную версию теоремы. Хотя трехмерного аналога комплексных чисел не существует, связь между положениями центров можно выразить в виде матричного уравнения, которое также обобщается до $n$ размеры.

Предположим, что в трех измерениях зафиксированы три взаимно касающиеся сферы, а четвертая сфера $S_{1}$ задана касательная к трем неподвижным сферам. Трехмерную версию теоремы Декарта можно применить для нахождения сферы. $S_{2}$ касательная к $S_{1}$ и фиксированные сферы, затем примененные снова, чтобы найти новую сферу $S_{3}$ касательная к $S_{2}$ и неподвижные сферы и так далее. Результатом является циклическая последовательность из шести сфер, каждая из которых касается своих соседей в последовательности и трех фиксированных сфер, конфигурация, названная гекслетом Содди , после открытия Содди и публикации ее в форме другого стихотворения в 1936 году.

Конфигурации взаимно касающихся гиперсфер более высокой размерности в сферической или гиперболической геометрии с кривизной, определенной выше , удовлетворяют

$${\biggl (}\sum _{i=1}^{n+2}k_{i}{\biggr )}^{\!2}=nC+n\,\sum _{i=1}^{n+2}k_{i}^{2},$$

где $C=2$ в сферической геометрии и $C=-2$ в гиперболической геометрии.

См. также

• Упаковка круга в круг
• Четырехквадратное тождество Эйлера
• круги Малфатти