Усеченный додекаэдр

Усеченный додекаэдр
Усеченный додекаэдр
Тип	Архимедово тело
Лица	32
Края	90
Группа симметрии	икосаэдрическая симметрия
Двугранный угол ( градусы )	10-10: 116.57° ; 3-10: 142.62°
Двойной многогранник	Триакис икосаэдр
Вершинная фигура
Сеть

В геометрии представляет усеченный додекаэдр собой архимедово тело . Он имеет 12 правильных десятиугольных граней, 20 правильных треугольных граней, 60 вершин и 90 ребер.

Строительство

Усечённый додекаэдр состоит из правильного додекаэдра путём отрезания всех его вершин — процесс, известный как усечение . ^{[ 1 ]} В качестве альтернативы усеченный додекаэдр можно построить путем расширения : отталкивая ребра правильного додекаэдра, превращая пятиугольные грани в десятиугольные грани, а вершины в треугольники . ^{[ 2 ]} Следовательно, у него 32 грани, 90 ребер и 60 вершин. ^{[ 3 ]}

Усеченный додекаэдр также можно построить с использованием декартовых координат . С длиной ребра $2\varphi -2$ с центром в начале координат, все они являются четными перестановками $\left(0,\pm {\frac {1}{\varphi }},\pm (2+\varphi )\right),\qquad \left(\pm {\frac {1}{\varphi }},\pm \varphi ,\pm 2\varphi \right),\qquad \left(\pm \varphi ,\pm 2,\pm (\varphi +1)\right),$ где ${\textstyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$ это золотое сечение . ^{[ 4 ]}

Характеристики

Площадь поверхности $A$ и объем $V$ усеченного додекаэдра с длиной ребра $a$ являются: ^{[ 3 ]} ${\begin{aligned}A&=5\left({\sqrt {3}}+6{\sqrt {5+2{\sqrt {5}}}}\right)a^{2}&&\approx 100.991a^{2}\\V&={\frac {5}{12}}\left(99+47{\sqrt {5}}\right)a^{3}&&\approx 85.040a^{3}\end{aligned}}$

Двугранный угол усеченного додекаэдра между двумя правильными додекаэдрическими гранями равен 116,57°, а между треугольником и додекаэдром - 142,62°. ^{[ 5 ]}

Усеченный додекаэдр представляет собой архимедово тело , то есть представляет собой высокосимметричный и полуправильный многогранник, в вершине которого встречаются две или более различных правильных многоугольных граней. ^{[ 6 ]} Он имеет ту же симметрию, что и правильный икосаэдр, икосаэдрическую симметрию . ^{[ 7 ]} Многоугольные грани, которые встречаются в каждой вершине, представляют собой один равносторонний треугольник и два правильных десятиугольника, а фигура вершины усеченного додекаэдра равна $3\cdot 10^{2}$ . Двойником усеченного додекаэдра является триакисикосаэдр , каталонское тело . ^{[ 8 ]} который имеет ту же симметрию, что и усеченный додекаэдр. ^{[ 9 ]}

Усеченный додекаэдр некирален , то есть конгруэнтен своему зеркальному изображению. ^{[ 7 ]}

Усеченный додекаэдрический граф

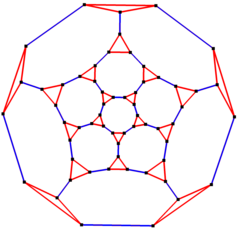
В математической области теории графов усеченный додекаэдрический граф — это граф вершин и ребер усеченного додекаэдра , одного из архимедовых тел . Он имеет 60 вершин и 90 ребер и представляет собой кубический архимедовый граф . ^{[ 10 ]}

Связанный многогранник

Усеченный додекаэдр можно применить в построении многогранника, известном как приращение . Примерами многогранников являются тела Джонсона , конструкции которых включаются путем прикрепления пятиугольных куполов к усеченному додекаэдру: расширенный усеченный додекаэдр , парабиувеличенный усеченный додекаэдр , метабиувеличенный усеченный додекаэдр и триаугментированный усеченный додекаэдр . ^{[ 3 ]}

См. также

Большой звездчатый усеченный додекаэдр

Ссылки

^ Зия, Юмит (2019). «Усеченный усеченный додекаэдр и усеченные пространства усеченного икосаэдра». Научный журнал Джумхуриет . 40 (2): 457–470. дои : 10.17776/csj.534616 .
^ Виана, Вера; Ксавье, Жоау Педро; Айрес, Ана Паула; Кампос, Хелена (2019). «Интерактивное разложение ахиральных многогранников» . В Коккьярелле, Луиджи (ред.). ICGG 2018 — Материалы 18-й Международной конференции по геометрии и графике: 40-летие — Милан, Италия, 3-7 августа 2018 г. п. 1122. дои : 10.1007/978-3-319-95588-9 . ISBN 978-3-319-95588-9 .
^ Перейти обратно: ^а ^б ^с Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329–352. дои : 10.1016/0016-0032(71)90071-8 . МР 0290245 . См., в частности, стр. 336.
^ Вайсштейн, Эрик В. «Группа икосаэдра» . Математический мир .
^ Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями». Канадский математический журнал . 18 : 169–200. дои : 10.4153/cjm-1966-021-8 . МР 0185507 . Збл 0132.14603 .
^ Дюдя, МВ (2018). Многооболочечные многогранные кластеры . Спрингер . п. 39 . дои : 10.1007/978-3-319-64123-2 . ISBN 978-3-319-64123-2 .
^ Перейти обратно: ^а ^б Коджа, М.; Коджа, НЕТ (2013). «Группы Кокстера, кватернионы, симметрии многогранников и 4D-многогранники» . Математическая физика: материалы 13-й региональной конференции, Анталья, Турция, 27–31 октября 2010 г. Всемирная научная. п. 48 .
^ Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. с. 88 . ISBN 978-0-486-23729-9 .
^ Холден, Алан (1991). Формы, пространство и симметрия . Дуврские книги по математике. Курьерская компания . п. 52 . ISBN 9780486268514 .
^ Читай, RC; Уилсон, Р.Дж. (1998). Атлас графов . Издательство Оксфордского университета . п. 269.

Дальнейшее чтение

Кромвель, П. (1997). Многогранники . Великобритания: Кембридж. С. 79–86 Архимедовы тела . ISBN 0-521-55432-2 .

Внешние ссылки

[ziya-1] Зия, Юмит (2019). «Усеченный усеченный додекаэдр и усеченные пространства усеченного икосаэдра». Научный журнал Джумхуриет . 40 (2): 457–470. дои : 10.17776/csj.534616 .

[vxac-2] Виана, Вера; Ксавье, Жоау Педро; Айрес, Ана Паула; Кампос, Хелена (2019). «Интерактивное разложение ахиральных многогранников» . В Коккьярелле, Луиджи (ред.). ICGG 2018 — Материалы 18-й Международной конференции по геометрии и графике: 40-летие — Милан, Италия, 3-7 августа 2018 г. п. 1122. дои : 10.1007/978-3-319-95588-9 . ISBN 978-3-319-95588-9 .

[berman-3] Перейти обратно: ^а ^б ^с Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329–352. дои : 10.1016/0016-0032(71)90071-8 . МР 0290245 . См., в частности, стр. 336.

[4] Вайсштейн, Эрик В. «Группа икосаэдра» . Математический мир .

[johnson-5] Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями». Канадский математический журнал . 18 : 169–200. дои : 10.4153/cjm-1966-021-8 . МР 0185507 . Збл 0132.14603 .

[diudea-6] Дюдя, МВ (2018). Многооболочечные многогранные кластеры . Спрингер . п. 39 . дои : 10.1007/978-3-319-64123-2 . ISBN 978-3-319-64123-2 .

[kk-7] Перейти обратно: ^а ^б Коджа, М.; Коджа, НЕТ (2013). «Группы Кокстера, кватернионы, симметрии многогранников и 4D-многогранники» . Математическая физика: материалы 13-й региональной конференции, Анталья, Турция, 27–31 октября 2010 г. Всемирная научная. п. 48 .

[williams-8] Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. с. 88 . ISBN 978-0-486-23729-9 .

[holden-9] Холден, Алан (1991). Формы, пространство и симметрия . Дуврские книги по математике. Курьерская компания . п. 52 . ISBN 9780486268514 .

[rw-10] Читай, RC; Уилсон, Р.Дж. (1998). Атлас графов . Издательство Оксфордского университета . п. 269.

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]